Привет!
Сегодня мы поговорим об амортизационном анализе. Сначала я расскажу, что это такое, и приведу игрушечный пример. А потом расскажу, как его применить для анализа системы непересекающихся множеств.
Амортизационный анализ
Амортизационный анализ применяют для алгоритмов, которые запускаются несколько раз. Время алгоритма может сильно колебаться, но мы оцениваем среднее или суммарное время по всем запускам. Чаще всего алгоритм реализует какую-нибудь операцию над структурой данных.
Само слово «амортизация» пришло из финансов. Оно означает небольшие периодические выплаты с целью погашения займа. В нешем случае оно означает, что быстрые операции своим временем компенсируют затраты на медленные.
Рассмотрим последовательность операций 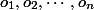 . Каждая операция
. Каждая операция 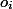 по факту выполняется за время
по факту выполняется за время 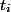 . Это время назовем фактическим. Для каждой операции
. Это время назовем фактическим. Для каждой операции 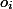 мы посчитаем амортизационное время
мы посчитаем амортизационное время 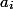 . Мы вводим это время, чтобы было проще оценить
. Мы вводим это время, чтобы было проще оценить 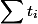 . Отсюда вытекают два ограничения: а) формальное — для любого момента
. Отсюда вытекают два ограничения: а) формальное — для любого момента 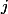 выполняется неравенство
выполняется неравенство 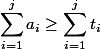 , и б) неформальное — сумма амортизационных стоимостей должна легко считаться.
, и б) неформальное — сумма амортизационных стоимостей должна легко считаться.
Чтобы иметь на глазах конкретный пример, рассмотрим структуру данных, внутри которой лежит стек. Структура данных поддерживает операцию op(m, x), которая выкидывает из стека последние 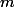 элементов, а затем вставляет элемент
элементов, а затем вставляет элемент  .
.
def op(stack, m, x):
for i in range(m):
stack.pop()
stack.push(x)
Мы будем считать, что аргументы всегда корректны, и от нас никогда не потребуют выкинуть больше, чем есть в стеке. Кроме того, будем считать, что op(m, x) выполняется за 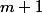 шаг без
шаг без 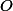 -нотации. Все наши оценки всегда можно домножить на константу, чтобы получить корректные.
-нотации. Все наши оценки всегда можно домножить на константу, чтобы получить корректные.
Заметим, что время операция op(m, x) может длиться от одного до 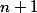 шага. Грубая оценка даст время
шага. Грубая оценка даст время 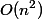 на выполнение всех
на выполнение всех 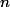 операций.
операций.
Амортизационный анализ предлагает три метода оценки.
Метод банкира. Время — деньги
Пусть каждая единица времени — это монета. Каждой операции выдадим 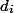 монет и разрешим тратить
монет и разрешим тратить 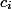 . Все свои монеты операции могут раскладывать по структуре данных. Амортизационная стоимость одной операции составит
. Все свои монеты операции могут раскладывать по структуре данных. Амортизационная стоимость одной операции составит 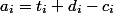 .
.
Чтобы поддержать инвариант 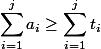 , мы зададим ограничение: нельзя потратить монет больше, чем их есть на текущий момент:
, мы зададим ограничение: нельзя потратить монет больше, чем их есть на текущий момент: 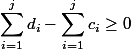 . Поскольку
. Поскольку 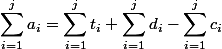 , то
, то 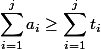 .
.
Для нашего примера мы выдадим каждой операции одну монету (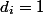 ). Положим ее на элемент, который только что добавили в стек. Таким образом, мы оплатили будущий POP этого элемента.
). Положим ее на элемент, который только что добавили в стек. Таким образом, мы оплатили будущий POP этого элемента.
Отметим, что в любой момент времени на каждом элементе стека лежит по монете, т.е. все POP-ы предоплачены.
Чтобы выкинуть 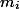 элементов мы потратим все монеты, которые лежат на них (
элементов мы потратим все монеты, которые лежат на них (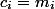 ). Тогда амортизационная стоимость каждой операции
). Тогда амортизационная стоимость каждой операции 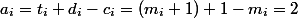 . Осталось заметить, что
. Осталось заметить, что 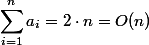 . Мы получили верхнюю линейную оценку на выполнение
. Мы получили верхнюю линейную оценку на выполнение 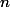 операций.
операций.
Метод физика. Используй свой потенциал
Любая структура данных может принимать несколько возможных состояний. Пусть 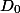 — это ее начальное состояние до всех операций, а
— это ее начальное состояние до всех операций, а 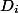 — состояние после
— состояние после 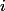 -ой операции. Мы введем функцию потенциала
-ой операции. Мы введем функцию потенциала 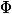 , которая принимает на вход текущее состояние структуры данных и возвращает некоторое неотрицательное число. Потенциал
, которая принимает на вход текущее состояние структуры данных и возвращает некоторое неотрицательное число. Потенциал 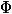 начального состояния должен быть равен нулю. Для простоты мы обозначим
начального состояния должен быть равен нулю. Для простоты мы обозначим 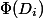 через
через 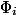 , а
, а 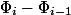 через
через 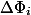 . Амортизационная стоимость
. Амортизационная стоимость 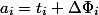 .
.
Инвариант 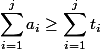 следует из определения потенциала. Действительно,
следует из определения потенциала. Действительно, 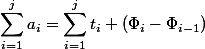 ; все
; все 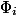 , кроме первого и последнего, сокращаются и
, кроме первого и последнего, сокращаются и 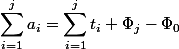 . Поскольку
. Поскольку 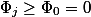 , то
, то 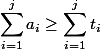 .
.
Общая идея, найти такую функцию потенциала, которая на дорогих операциях бы сильно падала, компенсируя фактическое время, а на дешевых немного росла. Для нашего примера подойдет число элементов в стеке. После 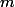
POP-ов и одного PUSH-а 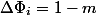 . Тогда амортизационная стоимость
. Тогда амортизационная стоимость 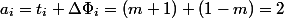 , и снова получаем линейную оценку.
, и снова получаем линейную оценку.
Агрегационный метод. Нужно все взять и поделить
Этот метод является обобщением двух предыдущих, и заключается в том, чтобы как-то посчитать 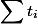 и поделить на число запросов.
и поделить на число запросов.
В нашем случае работает такое рассуждение. Каждая операция op(m, x) выполняет один PUSH и несколько POP-ов. Из стека нельзя выкинуть больше элементов, чем туда положили. Всего в стек положим 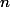 элементов, выкинем не больше
элементов, выкинем не больше 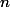 . Значит, суммарное время —
. Значит, суммарное время — 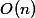 . Амортизационная стоимость одной операции
. Амортизационная стоимость одной операции 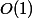 .
.
Система непересекающихся множеств
Нам дали 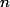 элементов. Элементы можно объединять в множества. Мы хотим сделать структуру данных, которая поддерживает три операции
элементов. Элементы можно объединять в множества. Мы хотим сделать структуру данных, которая поддерживает три операции
-
make_set(key)— создает множество из одного элемента, -
union(A, B)— объединяет множестваAиB, -
find(x)— возвращает множество, в котором лежит элемент .
.
Структуру данных, которая поддерживает эти операции, называют системой непересекающихся множеств (СНМ) (англ. disjoint-set data structure, union-find data structure или merge-find set).
На хабре уже писали про СНМ. Подробное описание алгоритма и его применения можно прочитать здесь. В этом посте я кратко напомню сам алгоритм и сконцентрирую внимание на анализе.
Алгоритм
Каждое множество мы будем хранить в виде дерева. Узел дерева хранит ссылку на родителя. Если узел — корень, ссылка указывают на None. Кроме того, у каждого узла будет дополнительное поле rank. Мы его обсудим ниже.
class Node:
def __init__(self, key):
self.parent = None
self.rank = 0
self.key = key
Чтобы обращаться с множествами, мы выберем для каждого множества по представителю. В нашем случае, это будет корень дерева. Если для двух элементов представитель совпадает, то они лежат в одном множестве. Чтобы объединить два множества, нужно подвесить одно дерево к корню другого. Получаем незатейливый алгоритм:
def find(x):
if x.parent == None:
return x
return find(x.parent)
def union(x, y):
x = find(x)
y = find(y)
y.parent = x
return x
Для ускорения алгоритма используют две эвристики.
Ранги. Каждому узлу назначим ранг, изначально равный нулю. Рангом дерева будет ранг его корня. При объединении множеств, будем подвешивать дерево меньшего ранга к дереву большего. Если ранги совпадают, то сначала увеличим ранг одного из деревьев на единицу.
def union(x, y):
x = find(x)
y = find(y)
if x.rank < y.rank:
x, y = y, x
if x.rank == y.rank:
x.rank += 1
y.parent = x
return x
Одной только ранговой эвристики хватит, чтобы ускорить работу СНМ до  на операцию в худшем случае. Но мы пойдем дальше.
на операцию в худшем случае. Но мы пойдем дальше.
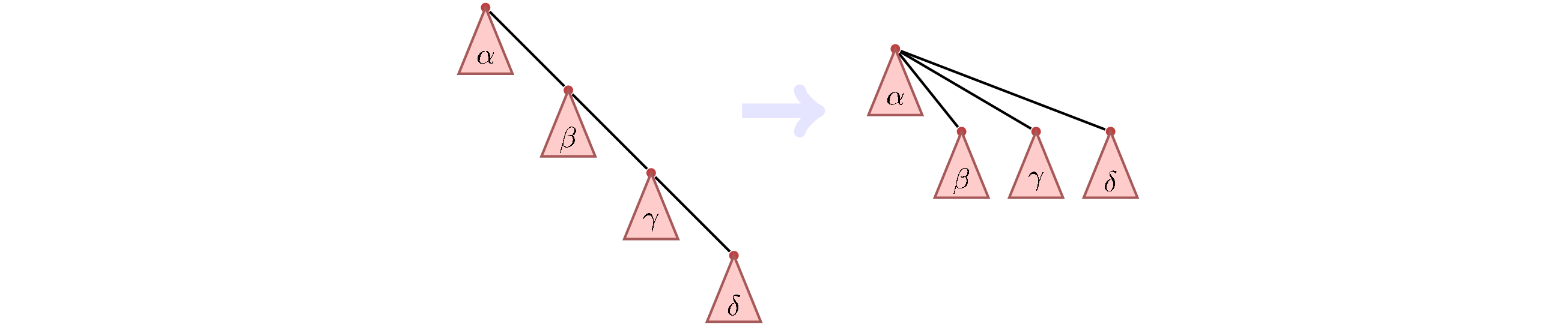
Сжатие путей. Пусть мы запустили find от элемента  . Можно заметить, что все вершины на пути от
. Можно заметить, что все вершины на пути от  до корня можно подвесить сразу к корню.
до корня можно подвесить сразу к корню.
def find(x):
if x.parent == None:
return x
x.parent = find(x.parent)
return x.parent
Удивительно, но вместе эти две эвристики сводят амортизационное время одной операции почти к константе.
Анализ
В 1973 году Хопкрофт и Ульман показали, что СНМ с двумя эвристиками обрабатывает  операций за
операций за  , где
, где  — итеративный логарифм. Позже, в 1975, Тарьян показал, что СНМ работает за
— итеративный логарифм. Позже, в 1975, Тарьян показал, что СНМ работает за  , где
, где  — обратная функция Аккермана.
— обратная функция Аккермана.
Мой план сначала разобрать, что это за хитрые функции, потом доказать простую логарифмическую оценку в худшем случае, а в конце разобрать оценку Хопкрофта и Ульмана. Оценка Тарьяна тоже активно использует амортизационный анализ, но содержит больше технических деталей.
Хитрые функции
Итеративный логарифм — эта функция, обратная степенной башне. Давайте представим себе число вида  , где всего двоек будет
, где всего двоек будет  . Тогда
. Тогда  — это минимальное такое
— это минимальное такое  , что степенная башня высоты
, что степенная башня высоты  будет больше
будет больше  . Формально
. Формально
-
 для любого
для любого  ;
; -
 для
для  .
.
Упражнение читателю, показать, что итеративный логарифм от числа частиц в известной нам части вселенной не превосходит пяти.
Можно подумать, что степенная башня растет быстро, но математикам начала двадцатого века этого было мало, и они придумали функцию Аккермана. Определяется она так:
-
 для
для  ;
; -
 для
для  ;
; -
 для
для  .
.
Эта функция растет очень быстро. При  , она является степенной башней. При
, она является степенной башней. При  она тоже является степенной башней, только теперь число двоек в башне — тоже степенная башня и т.д.
она тоже является степенной башней, только теперь число двоек в башне — тоже степенная башня и т.д.
Хотите отомстить врагу, попросите его посчитать эту функцию, используя только арифметические операции, if-ы и for-ы (while-ы и рекурсию нельзя). Аккерман доказал, что он провалится.
Обратная функция Аккермана  определяется как минимальное
определяется как минимальное  такое, что
такое, что  . Несложно понять, что растет она очень медленно.
. Несложно понять, что растет она очень медленно.
Оценка в худшем случае
Сначала заметим, что каждый union делается за две операции find и некоторую дополнительную константу времени. Значит, достаточно оценить только find. Оценка в худшем случае следует из двух простых наблюдений.
Наблюдение 1. Дерево ранга  содержит не менее
содержит не менее  узлов.
узлов.
Это утверждение доказывается по индукции. Для дерева ранга 0, очевидно. Чтобы получить дерево ранга  , нужно объединить два дерева ранга
, нужно объединить два дерева ранга  , в каждом из которых хотя бы
, в каждом из которых хотя бы  узлов. Значит, в дереве ранга
узлов. Значит, в дереве ранга  окажется хотя бы
окажется хотя бы  узлов.
узлов.
Как следствие, в любой момент времени узлов ранга  будет не более
будет не более  , и максимальный ранг узла
, и максимальный ранг узла  .
.
Замечание 2. Ранг родителя всегда больше ранга ребенка.
Следует из построения. Поскольку на пути от вершины к корню ранг всегда увеличивается, то его длина не превосходит  , и любой
, и любой find работает за  .
.
Оценка Хопкрофта и Ульмана
Докажем, что  операций СНМ над
операций СНМ над  элементами можно провести за
элементами можно провести за  .
.
Операция make_set выполняется за  . Операция
. Операция union — за  плюс время двух операций
плюс время двух операций find. Значит, достаточно показать, что  операций
операций find будут выполняться за  .
.
Время выполнения операции find пропорционально длине пути, который требуется пройти от заданного узла до корня. Поэтому нужно оценивать суммарное число проходов по узлам.
Разобъем все ранги на  множеств:
множеств:  . В
. В  -ом множестве будут находиться все ранги от степенной башни
-ом множестве будут находиться все ранги от степенной башни  высоты
высоты  до башни высоты
до башни высоты  . Номер множества, в котором лежит ранг узла, назовем уровнем узла.
. Номер множества, в котором лежит ранг узла, назовем уровнем узла.
Будем говорить, что узел — хороший, если он является корнем дерева, непосредственным ребенком корня, или он и его родитель имеют разные уровни. Оставшиеся узлы назовем плохими.
Всего уровней не больше  . Значит, путь от любого узла до корня содержит не более
. Значит, путь от любого узла до корня содержит не более  хороших узлов. В сумме
хороших узлов. В сумме find пройдет не более  хороших узлов.
хороших узлов.
Оценим число проходов по плохим узлам. Пусть плохой узел  имеет ранг
имеет ранг  , и
, и  принадлежит множеству
принадлежит множеству  . Заметим, что плохой узел не является корнем, и потому его ранг фиксирован. Если
. Заметим, что плохой узел не является корнем, и потому его ранг фиксирован. Если find проходит по узлу  , то
, то  меняет своего родителя на нового с большим рангом. Не более, чем за
меняет своего родителя на нового с большим рангом. Не более, чем за  проходов по
проходов по  , как по плохому узлу,
, как по плохому узлу,  станет хорошим.
станет хорошим.
Всего узлов ранга  не более
не более  . Значит узлов с рангами из множества
. Значит узлов с рангами из множества  будет не более
будет не более  . На каждый узел приходится не более
. На каждый узел приходится не более  проходов, как по плохому узлу. Значит в сумме проходов будет не более
проходов, как по плохому узлу. Значит в сумме проходов будет не более  . Всего уровней
. Всего уровней  . Значит, проходов по плохим узлам будет не более
. Значит, проходов по плохим узлам будет не более  .
.
Итого, получили верхнюю оценку  на все операции в сумме.
на все операции в сумме.
Литература
- Кормен, Лейзерсон, Ривест «Алгоритмы: построение и анализ»
- Tarjan «Data Structures and Network Algorithms»
- Rebecca Fiebrink «Amortized Analysis Explained»
Автор: SeptiM






