В.А. Малых, Д.Л. Шоломов, В.В. Арлазаров

Для достижения хорошего качества распознавания критически важных полей на формах необходимо использовать дополнительную информацию. Зачастую для этого в формат распознаваемого поля специально вводится проверочный разряд или иная избыточная информация.
В данной статье предложен универсальный алгоритм «рулетки» для распознавания полей с проверочной функцией.
В статье также приведены результаты практической апробации предложенного алгоритма и, кроме того, дана общая классификация проверочных алгоритмов.
Введение
В современной постановке задача распознавания стоит, прежде всего, для так называемых бизнес-форм. То есть документов коммерческого свойства, прежде всего финансовых. Примером бизнес-формы может служить товарная накладная, которая является одним из основных видов документов, используемых в торговле.
Для бизнес-форм характерна неравнозначность информации, расположенной в различных полях формы. Прежде всего, важными полями являются поля сумм, номеров счетов и т.п. Примером критически важного поля может служить номер паспорта в форме, где используются паспортные данные.
Для повышения качества распознавания критически важных полей форм применяются различные методы. В частности, используются методы с введением в данные дополнительной избыточной информации. Широко известным примером такого метода из области теории информации являются коды Хемминга [3]. Ряд методов в области распознавания текстов предложен в работе [1].
Применительно к задаче распознавания существует класс полей, содержащий в самой своей структуре дополнительную информацию, которая может служить для проверки корректности распознавания. А также для исправления ошибок, если ставится такая задача.
Можно разделить использование дополнительной информации условно на два типа – корректирующая и отбраковывающая проверки. Для отбраковывающей проверки характерно использование заранее предопределённых значений на соответствие (например, широко распространённая проверка по словарю). В этом случае при отсутствии полученного при распознавании значения в словаре, мы выносим решение о некорректности распознавания.
Корректирующая проверка отличается от отбраковывающей тем, что мы можем попытаться восстановить неправильно распознанное значение.
Для каждого символа существуют альтернативы распознавания. Можно проверить значение, заменив один (или несколько) символ на его альтернативу. Такой метод, примененный к значению без контрольных данных значительно менее результативен – так как мы фактически пытаемся угадать, что же было распознано неправильно. В силу того, что вероятность ошибки, прежде всего, зависит от самого символа, то сделать однозначный вывод о том, какой из символов был распознан некорректно исходя из общих соображений нельзя. С другой стороны, имея контрольную информацию, мы можем проверить корректность замены символа на его альтернативу.
В силу того, что алгоритм контрольного значения выбирается с тем расчётом, чтобы близкие значения основных данных соответствовали существенно отличным контрольным данным, и, принимая во внимание малую вероятность ошибки, мы приходим к тому, что может восстановить изначальные данные с большой долей уверенности.
Такая дополнительная информация может быть выражена в любой форме, но наибольшее распространение получили так называемые контрольные суммы.
Математическая постановка задачи
Постановка задачи распознавания в наиболее общем виде дается, например, в [4]. В статье используется узкая постановка задачи из [5]. Задача распознавания с коррекцией сводится к перебору элементов вектора альтернатив 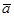 для каждого символа
для каждого символа 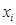 из слова
из слова 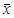 . Для каждого набора
. Для каждого набора 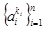 , где
, где 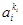 –
– 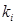 -ый элемент вектора
-ый элемент вектора 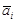 , соответствующего
, соответствующего 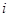 -ому распознаваемому символу, который мы будем называть интерпретацией, производится его преобразование в линейную последовательность, которая подвергается соответствующей проверке
-ому распознаваемому символу, который мы будем называть интерпретацией, производится его преобразование в линейную последовательность, которая подвергается соответствующей проверке
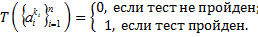
Общее количество возможных интерпретаций задается формулой 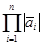 , где
, где 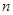 — количество символов в слове
— количество символов в слове 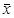 .
.
Уже для 2 вариантов для каждого символа слова длиной 15 символов эта формула даёт 32768 вариантов интерпретации, что, при достаточно сложной функции проверки 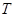 , может приводить к длительным задержкам при распознавании. Но, как показывает опыт практического применения, большая часть слов распознается при проверке одного варианта для каждого символа, т.е. для слова длиной символов нужно рассмотреть всего лишь порядка 15 вариантов распознавания.
, может приводить к длительным задержкам при распознавании. Но, как показывает опыт практического применения, большая часть слов распознается при проверке одного варианта для каждого символа, т.е. для слова длиной символов нужно рассмотреть всего лишь порядка 15 вариантов распознавания.
Алгоритм корректировки
Алгоритм, предлагаемый для отбраковки и/или восстановления данных с контрольными значениями.
В силу того, что вероятность ошибки в любом символе одинакова, алгоритмом не делается различие контрольных и ординарных разрядов. Алгоритм последовательно сменяет альтернативы, комбинируя их для всех символов до тех пор, пока комбинация альтернатив не удовлетворит используемой проверке. В силу сложности алгоритма проверки контрольного разряда существует возможность существенно понизить вероятность неверного распознавания.
Принцип работы алгоритма сводится к последовательному перебору вариантов интерпретации слова 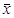 и применения к ним проверки
и применения к ним проверки 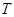 . При описании алгоритма, с использованием псевдо-кода слово
. При описании алгоритма, с использованием псевдо-кода слово 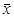 обозначено как RecognitionResult, а функция проверки
обозначено как RecognitionResult, а функция проверки 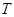 обозначена как Test.
обозначена как Test.
Roulette(Test, RecognitionResult)
CharCounter[RecognitionResult.Length]
for i = 0 to RecognitionResult.Length
charCounter[i] = 0
while Test(RecognitionResult) is not true
if UpdateCounter(CharCounter, RecognitionResult, 0) is not true
break
else
for i = 0 to RecognitionResult.Length
//Присваиваем значение тестируемого альтернативного
//значения распознанного символа его значению по умолчанию
RecognitionResult.Char[i].Alt[0] =
RecognitionResult.Char[i].Alt[CharCounter[i]]
В алгоритме используется вспомогательная функция UpdateCounter, с помощью которой непосредственно производится перебор интерпретаций:
UpdateCounter(CharCounter, RecognitionResult, i)
if CharCounter[i] < RecognitionResult.Char[i].Length)
CharCounter[i] = CharCounter[i] + 1
return true
else
if i < RecognitionResult.Length - 1
CharCounter[i] = 0
return UpdateCounter(CharCounter, RecognitionResult, i+1)
else
return false
Алгоритм, под названием Roulette, принимает на вход два параметра:
- результат распознавания, представленный как вектор векторов альтернатив распознавания символов, т.е. для каждого из символов существует свой вектор альтернатив; он обозначен как RecognitionResult;
- функцию проверки, принимающую на вход одно значение и выдающую бинарный результат прохождения; обозначена как Test.
RecognitionResult содержит в себе массив Char и длину массива Char, заданную как Length. Массив Char содержит в каждом своем элементе массив альтернатив распознавания символа Alt. Каждый элемент массива Char содержит в себе длина массива альтернатив Alt, заданную как Length.
Предполагается, что функция проверки Test принимает на вход только результат распознавания RecognitionResult и производит проверку по значениям по умолчанию элементов массива Char в нем.
Пример практического применения
Рассмотрим пример контрольной суммы для ИНН и её корректирующей проверки.
Алгоритм вычисления контрольной суммы следующий (для 12-значного кода):
Шаг 1. Контрольное число n2 есть остаток от деления на 11 суммы из цифр номера, умноженных на соответствующие коэффициенты из таблицы 1 (из строки «вычисление контрольного числа n2»). Если остаток есть 10, то n2 = 0.
Шаг 2. Контрольное число n1 есть остаток от деления на 11 суммы из цифр номера, умноженных на соответствующие коэффициенты из таблицы 1 (из строки «вычисление контрольного числа n1»). Если остаток есть 10, то n1 = 0.
Таблица 1.
| k12 | k11 | k10 | k9 | k8 | k7 | k6 | k5 | k4 | k3 | k2 | k1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| вычисление контрольного числа n2 для 12-значного ИНН |
7 | 2 | 4 | 10 | 3 | 5 | 9 | 4 | 6 | 8 | ||
| вычисление контрольного числа n1 для 12-значного ИНН |
3 | 7 | 2 | 4 | 10 | 3 | 5 | 9 | 4 | 6 | 8 | |
| вычисление контрольного числа n1 для 10-значного ИНН |
В случае 10-значного ИНН имеется один контрольный разряд, в случае 12-значного – два контрольных разряда. Коэффициенты для вычисления контрольного разряда представлены в таблице 1.
Пример изображения, поступающего на вход распознающему алгоритму:
Изображение 1.

На изображении 1 можно выделить две потенциальных проблемы распознавания (список неисчерпывающий):
- третья позиция «3» интерпретирована, как «5», у которой исчезла верхняя черта;
- восьмая позиция «7» интерпретирована, как «2» с незавершённой соединительной петлёй.
Пусть реализовалась первая из описанных проблем – произошла ошибка в распознавании третьей позиции. Дополнительно предположим, что все позиции, кроме третьей, распознались однозначно. Соответственно, у нас есть альтернатива распознавания в третьей позиции.
Сделаем проверку для распознанного значения: «5253000796»
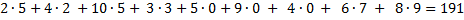
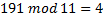
Откуда видно, что контрольная сумма не сошлась.
Теперь пробуем заменить символы на их альтернативы, то есть по нашему допущению, теперь проверяем значение «5233000796»
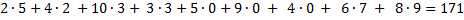
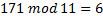
Таким образом, мы сумели скорректировать неправильно распознанное значение, используя проверочный разряд в нём.
Практическое применение алгоритма
Результаты работы нашли применение в промышленной системе Cognitive Forms, где описанный алгоритм используется для дополнительной проверки на типах полей ИНН, ОГРН и СНИЛС в различных реально существующих бизнес-формах. Система Cognitive Forms описана в статье [2].
Дополнительно было произведено тестирование на стенде объёмом 480 изображений (больничных листов), где проверялось распознавание полей вышеописанных типов. Результаты тестирования представлены в таблице 2.
Таблица 2.
| Общее число полей | 3840 |
| Количество правильно распознанных полей без подключенного алгоритма (б/а) |
3510 (91.41%) |
| Кол-во неправильно распознанных полей б/а | 330 (8.59%) |
| Из них неправильно без сомнения | 171 (4.45%) |
| Кол-во правильно распознанных полей с подключенным алгоритмом (с/а) |
3576 (93.12%) |
| Кол-во неправильно распознанных полей с/а | 264 (6.88%) |
| Из них неправильно без сомнения | 55 (1.43%) |
По результатам исследования видно, что с применением описанного алгоритма удалось повысить качество распознавания по этим полям более чем на 20% (с 91.41% до 93.12%) и, помимо этого, более чем втрое (с 4.45% до 1.43%) сократить количество неправильно распознанных без сомнения полей.
Заключение
В дальнейшем планируется улучшить распознавание полей с помощью этого алгоритма, а также расширить его применение на другие типы полей.
Литература:
1. Шоломов Д.Л. Синтаксические методы контекстной обработки в задачах распознавания текста. — М., 2007.
2. Арлазаров В. В., Постников В. В., Шоломов Д. Л. Cognitive Forms — cистема массового ввода структурированных документов. //"Управление информационными потоками" Сборник трудов Института системного анализа РАН./ М., УРСС, 2002 г.
3. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976.
4. Хайкин С. Нейронные сети. — М.: Вильямс, 2006.
5. Арлазаров В.В. Структурирование визуальных представлений информационной среды и методы определения надежности распознавания. — М., 2004.
Один из авторов статьи В.Малых присутствует на хабре — madrugado
Автор: Angelina54






