Все чаще и чаще мы сталкиваемся с необходимостью выявлять внутренние закономерности больших объёмов данных. Например, для распознавания спама необходимо уметь находить закономерности в содержании электронных писем, а для прогнозирования стоимости акций — закономерности в финансовых данных. К сожалению, выявить их «вручную» часто невозможно, и тогда на помощь приходят методы машинного обучения. Они позволяют строить алгоритмы, которые помогают находить новые, ещё не описанные закономерности. Мы поговорим о том, что такое машинное обучение, где его стоит применять и какие сложности могут при этом возникнуть. Принципы работы нескольких популярных методов машинного обучения будут рассмотрены на реальных примерах.
Лекция предназначена для старшеклассников — студентов Малого ШАДа, но и взрослые с ее помощью смогут составить представление об основах машинного обучения.
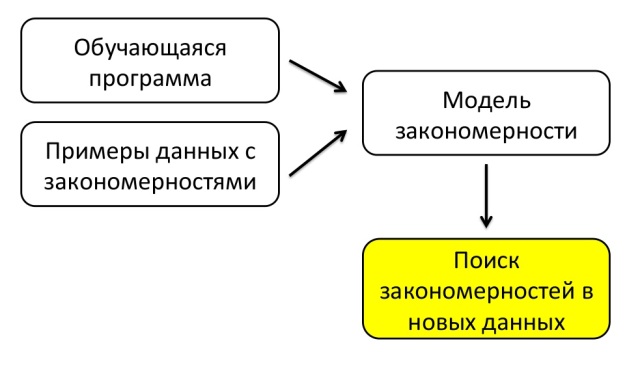
Основная идея машинного обучения заключается в том, что имея обучающуюся программу и примеры данных с закономерностями, мы можем построить некоторую модель закономерности и находить закономерности в новых данных.
Метод ближайшего соседа
Для примера решим простую задачу. У нас на плоскости разбросаны точки двух цветов: красные и синие. Координаты и цвет каждой из них нам известны. Нужно определить цвет новой точки. Каждая точка — изучаемый объект, а координаты и цвет — его параметры. Например, объекты — люди, координаты — рост и длина волос человека, а цвет — пол человека.
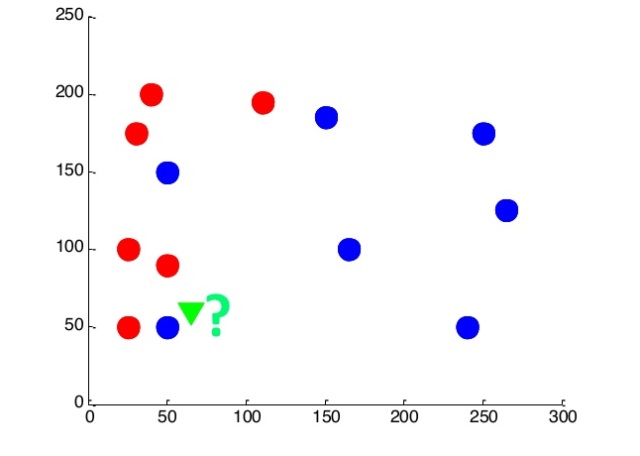
Попробуем решить ее методом ближайшего соседа. Пусть новый объект принадлежит к тому же классу, что и его ближайший сосед. Сделаем прогноз для каждой точки на нашей плоскости: если ближайшая точка синяя, значит, и новый объект, появившийся в этой точке – синий. И наоборот.
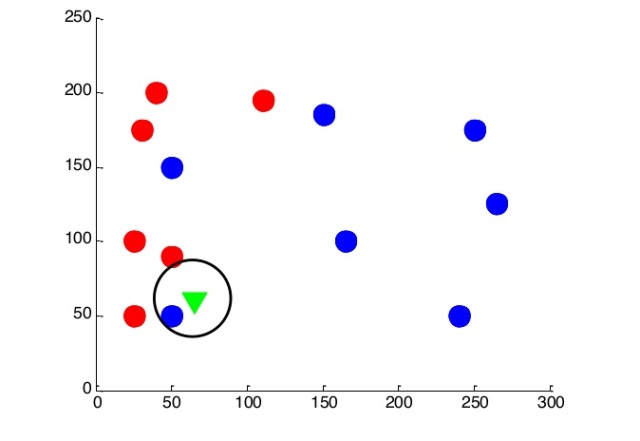
Таким образом, у нас получаются две области: в одной велика вероятность появления красных точек, а в другой – синих.
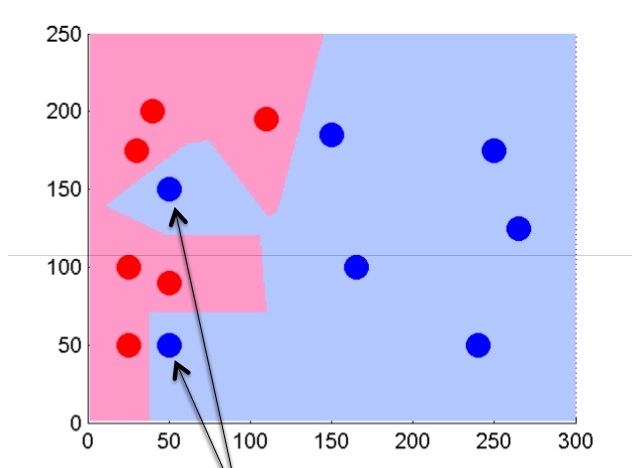
Далее попробуем немного изменить алгоритм, и ориентироваться на несколько (k) ближайших соседей. Пускай k будет равно пяти.
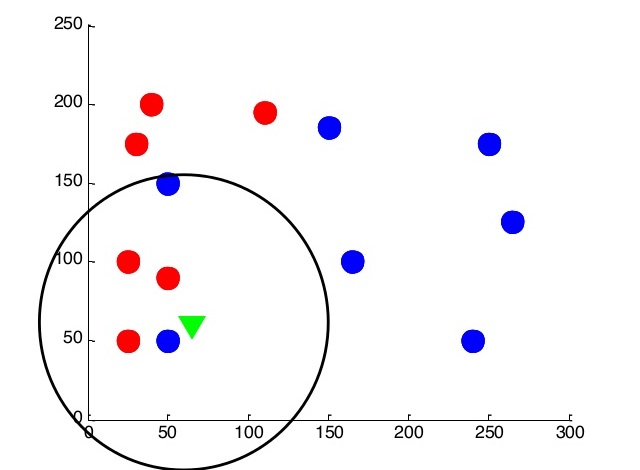
В этом случае мы сможем отсечь потенциально шумовые объекты и получить более ровную границу разделения классов.
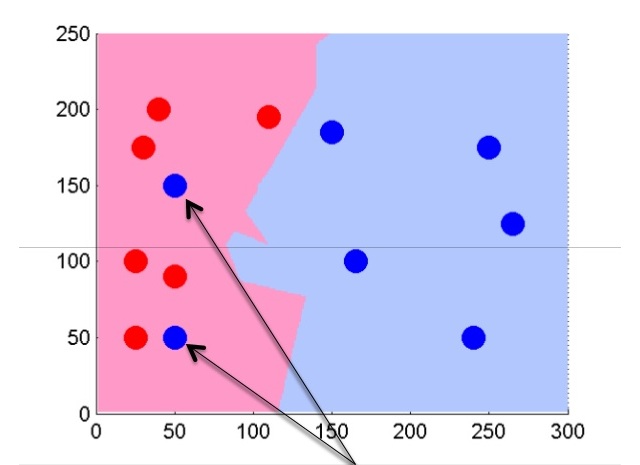
Вот так будет выглядеть разделение на большем количестве объектов, полученных путем нормального распределения.
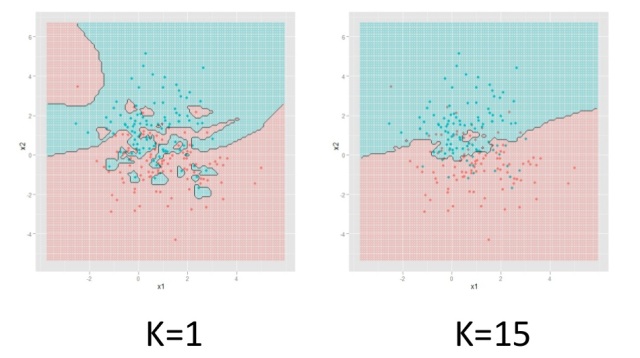
Качество и параметры алгоритмов
Снова представим, что у нас есть плоскость, на которой определенным образом расположены красные и синие точки.

Провести границу между ними можно разными способами. Результат будет зависеть от того, насколько алгоритм подстроился под данные.
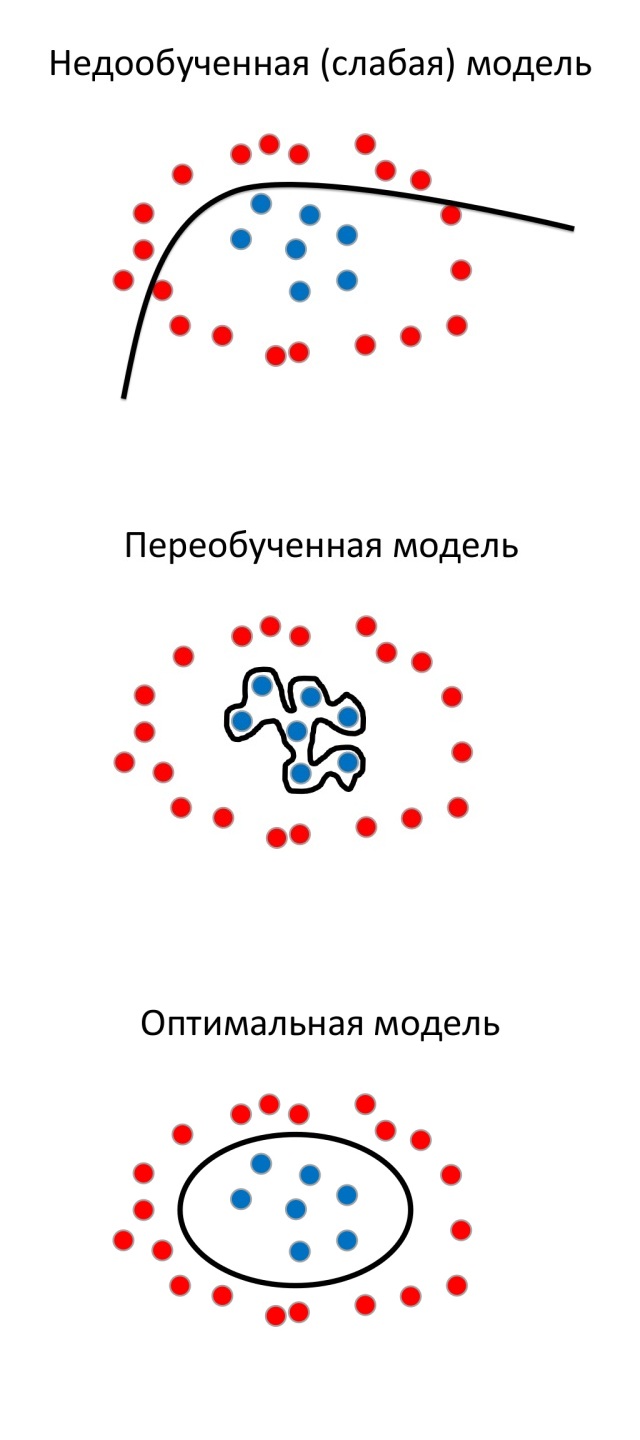
Как правило, склонность модели к переобучению связана с количеством ее параметров. Так, например, модель с малым количеством параметров вряд ли сможет переобучиться
В общем случае в задачах машинного обучения рассматриваются точки в многомерном пространстве, а не на плоскости. Каждая координата — признак. Поэтому обучающую выборку можно представлять в следующей виде:
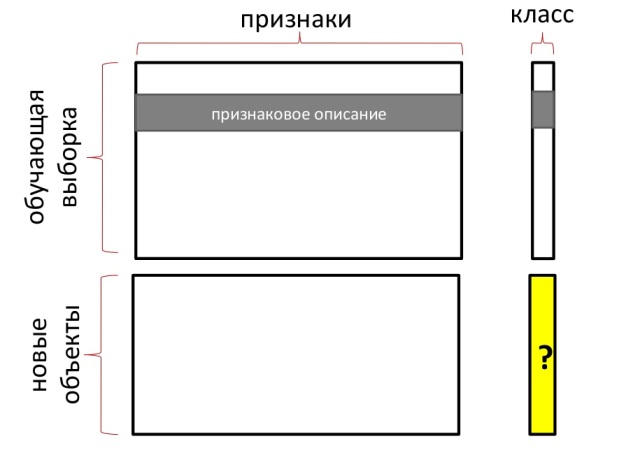
Но какой алгоритм выбрать, и как оценить качество его работы? Для этого размеченную обучающую выборку разбивают на две части. На первой части происходит непосредственно обучение, а вторая часть используется в качестве контрольной. На ней мы будем проверять, сколько ошибок выдал алгоритм.
Цикл решения задачи
Примерный цикл решения задачи по машинному обучению выглядит так:
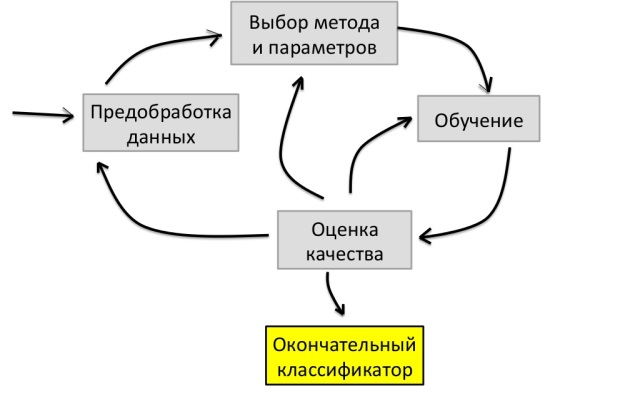
Сначала мы проводим предварительную обработку данных, затем выбираем метод классификации и параметры, проводим обучение и оцениваем качество. Если качество нас утраивает, задача считается выполненной. В противном случае возвращаемся к подбору метода и параметров.
Более подробная информация, примеры реальных задач для машинного обучения, а также рассказ о гиперплоскостях, нейронных сетях. deep learning, методе Виолы-Джонса, решающих деревьях и бустинге доступны в видеозаписи лекции.
Автор: elcoyot