Введение
Ранее во вступительной статье я поднимал список проблем, с которыми придется столкнуться разработчику, если он захочет оптимизировать оптимизацию обработки изображения при помощи SIMD инструкций. Теперь пришло время на конкретном примере показать, как указанные выше проблемы можно решить. Я долго думал, какой алгоритм выбрать для первого примера, и решил остановиться на медианной фильтрации. Медианная фильтрация является эффективным способом подавления шумов, которые неизбежно появляются на цифровых камерах в условиях малого освещения сцены. Алгоритм этот достаточно ресурсоемок – так например, при обработке серого изображения медианным фильтром 3х3 требуется порядка 50 операций на одну точку изображения. Но в тоже время он оперирует только с 8-битными числами и ему для работы требуется сравнительно не много входных данных. Эти обстоятельства делают алгоритм достаточно простым для SIMD оптимизации и в тоже время позволяют получить из нее весьма существенное ускорение.
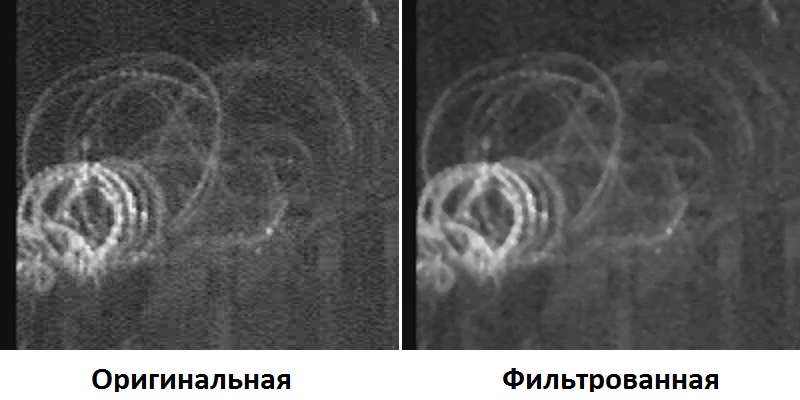
Для справки напоминаю суть алгоритма:
- Для каждой точки исходного изображения берется некоторая окрестность (в нашем случае 3x3).
- Точки данной окрестности сортируются по возрастанию яркости.
- Средняя точка (5-я для фильтра 3х3) отсортированной окрестности записывается в итоговое изображение.
Для первого примера, я решил упростить задачу и рассмотреть случай серого изображения (8 бит на точку) без учета граничных эффектов — для этого для фильтрации бралась центральная часть несколько большего изображения. Конечно, в реальных задачах граничные точки изображения следует рассчитывать по особому алгоритму, и порой реализация этих особых алгоритмов может занимать большую часть кода, но мы остановимся на этих вопросах в другой раз. Кроме того, по аналогичным причинам предполагается, что ширина изображения кратна 32.
Скалярные версии алгоритма
1-я скалярная версия
В этой начальной реализации задача была решена в лоб: окрестность для каждой точки исходного изображения копировалась во вспомогательный массив, который затем сортировался при помощи функции std::sort().
inline void Load(const uint8_t * src, int a[3])
{
a[0] = src[-1];
a[1] = src[0];
a[2] = src[1];
}
inline void Load(const uint8_t * src, size_t stride, int a[9])
{
Load(src - stride, a + 0);
Load(src, a + 3);
Load(src + stride, a + 6);
}
inline void Sort(int a[9])
{
std::sort(a, a + 9);
}
void MedianFilter(const uint8_t * src, size_t srcStride, size_t width, size_t height, uint8_t * dst, size_t dstStride)
{
int a[9];
for(size_t y = 0; y < height; ++y)
{
for(size_t x = 0; x < width; ++x)
{
Load(src + x, srcStride, a);
Sort(a);
dst[x] = (uint8_t)a[4];
}
src += srcStride;
dst += dstStride;
}
}
2-я скалярная версия
У предыдущего метода, впрочем, сразу видно узкое место – это стандартная функции сортировки. Она предназначена для сортировки массива произвольного размера, в ней осуществляется множество внутренних проверок, поэтому она, скорее всего, не будет оптимальным решением для данной задачи, где массив мал и имеет фиксированный размер. Кроме того, нам совсем не обязательно полностью сортировать массив, достаточно, что бы в 4-м элементе было требуемое нами значение. Потому мы можем применить метод сортировки «сетью» (так же известен, как метод битонической сортировки):
inline void Sort(int & a, int & b) // сортирует пару чисел
{
if(a > b)
{
int t = a;
a = b;
b = t;
}
}
inline void Sort(int a[9]) //частично сортирует весь массив
{
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]);
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]);
Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]);
Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]);
Sort(a[4], a[2]);
}
3-я скалярная версия
Хотя первый метод и получился значительно быстрее нулевого (см. результат тестирования ниже), но у него осталось одно узкое место – в этом методе очень много условных переходов. Как известно, современные процессоры очень их не любят, так как имеют конвейерную архитектуру и возможность внеочередного исполнения нескольких команд за один такт. И для первого, и для второго условные переходы крайне нежелательны, так как процессор должен останавливаться и ждать результатов вычислений, чтобы узнать по какой ветке программы ему следует идти дальше. К счастью сортировку двух 8 битных значений вполне можно реализовать и без условных переходов:
inline void Sort(int & a, int & b)
{
int d = a - b;
int m = ~(d >> 8);
b += d&m;
a -= d&m;
}
Итогом этих предварительных оптимизаций скалярно кода, будет следующая версия медианного фильтра:
inline void Load(const uint8_t * src, int a[3])
{
a[0] = src[-1];
a[1] = src[0];
a[2] = src[1];
}
inline void Load(const uint8_t * src, size_t stride, int a[9])
{
Load(src - stride, a + 0);
Load(src, a + 3);
Load(src + stride, a + 6);
}
inline void Sort(int & a, int & b)
{
int d = a - b;
int m = ~(d >> 8);
b += d&m;
a -= d&m;
}
inline void Sort(int a[9]) //частично сортирует весь массив
{
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]);
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]);
Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]);
Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]);
Sort(a[4], a[2]);
}
void MedianFilter(const uint8_t * src, size_t srcStride, size_t width, size_t height, uint8_t * dst, size_t dstStride)
{
int a[9];
for(size_t y = 0; y < height; ++y)
{
for(size_t x = 0; x < width; ++x)
{
Load(src + x, srcStride, a);
Sort(a);
dst[x] = (uint8_t)a[4];
}
src += srcStride;
dst += dstStride;
}
}
Данная версия уже значительно (где-то в 5-6 раз) опережает по скорости наш первоначальный вариант алгоритма. И именно основываясь на нем мы будем осуществлять SIMD оптимизацию алгоритма, а также осуществлять сравнение по скорости работы скалярной и векторной версии алгоритма.
SIMD версии алгоритма
Для иллюстрации оптимизации алгоритма медианной фильтрации при помощи SIMD, я задействую два набора инструкций SSE2 и AVX2, упустив расширение MMX, которое в настоящее время устарело и имеет больше исторический интерес.К счастью, для того, чтобы задействовать SIMD инструкции, совсем не обязательно использовать ассемблер. Большинство современных С++ компиляторов имеют поддержку intrinsics (встроенных функций, с помощью которых можно задействовать всевозможные расширения процессоров). Программирование с использованием intrinsics практически не отличается от программирования на чистом С. Intrinsic функции преобразуются компилятором напрямую в инструкции процессора, хотя при этом работа непосредственно с регистрами процессора остается скрытой от программиста. В большинстве случаев программа с использованием intrinsics не уступает в быстродействии программе, написанной на ассемблере.
SSE2 версия
Целочисленные команды SSE2 определены в заголовочном файле < emmintrin.h >. В качестве базового типа выступает __m128i — 128 битный вектор, который в зависимости от контекста может интерпретироваться как набор 2-х 64 битных, 4-х 32 битных, 8-х 16 битных, 16-х 8 битных знаковых или беззнаковых чисел. Как видно, поддерживают не только векторные арифметические операции, но также векторные логические операции, а также векторные операции загрузки и выгрузки данных. Ниже приведен оптимизации медианного фильтра при помощи SSE2 инструкций. Код, как мне кажется, довольно нагляден.
#include < emmintrin.h >
inline void Load(const uint8_t * src, __m128i a[3])
{
a[0] = _mm_loadu_si128((__m128i*)(src - 1)); //загрузка 128 битного вектора по невыровненному по 16 битной границе адресу
a[1] = _mm_loadu_si128((__m128i*)(src));
a[2] = _mm_loadu_si128((__m128i*)(src + 1));
}
inline void Load(const uint8_t * src, size_t stride, __m128i a[9])
{
Load(src - stride, a + 0);
Load(src, a + 3);
Load(src + stride, a + 6);
}
inline void Sort(__m128i& a, __m128i& b)
{
__m128i t = a;
a = _mm_min_epu8(t, b); //нахождение минимума 2-х 8 битных беззнаковых чисел для каждого из 16 значений вектора
b = _mm_max_epu8(t, b); //нахождение максимума 2-х 8 битных беззнаковых чисел для каждого из 16 значений вектора
}
inline void Sort(__m128i a[9]) //частично сортирует весь массив
{
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]);
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]);
Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]);
Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]);
Sort(a[4], a[2]);
}
void MedianFilter(const uint8_t * src, size_t srcStride, size_t width, size_t height, uint8_t * dst, size_t dstStride)
{
__m128i a[9];
for(size_t y = 0; y < height; ++y)
{
for(size_t x = 0; x < width; x += sizeof(__m128i))
{
Load(src + x, srcStride, a);
Sort(a);
_mm_storeu_si128((__m128i*)(dst + x), a[4]); //сохранение 128 битного вектора по невыровненному по 16 битной границе адресу
}
src += srcStride;
dst += dstStride;
}
}
AVX2 версия
Целочисленные команды AVX2 определены в заголовочном файле < immintrin.h >. В качестве базового типа выступает __m256i — 256 битный вектор, который в зависимости от контекста может интерпретироваться как набор 4-х 64 битных, 8-х 32 битных, 16-х 16 битных, 32-х 8 битных знаковых или беззнаковых чисел. Хотя набор инструкций AVX2 во многом повторяет набор инструкций SSE2 (с учетом удвоившейся ширины вектора), но он также содержит и достаточно много инструкций, у которых нет аналогов в SSE2. Ниже приведена оптимизация медианного фильтра при помощи AVX2 инструкций.
#include < immintrin.h >
inline void Load(const uint8_t * src, __m256i a[3])
{
a[0] = _mm256_loadu_si256((__m128i*)(src - 1)); //загрузка 256 битного вектора по невыровненному по 32 битной границе адресу
a[1] = _mm256_loadu_si256((__m128i*)(src));
a[2] = _mm256_loadu_si256((__m128i*)(src + 1));
}
inline void Load(const uint8_t * src, size_t stride, __m256i a[9])
{
Load(src - stride, a + 0);
Load(src, a + 3);
Load(src + stride, a + 6);
}
inline void Sort(__m256i& a, __m256i& b)
{
__m256i t = a;
a = _mm256_min_epu8(t, b); //нахождение минимума 2-х 8 битных беззнаковых чисел для каждого из 32 значений вектора
b = _mm256_max_epu8(t, b); //нахождение максимума 2-х 8 битных беззнаковых чисел для каждого из 32 значений вектора
}
inline void Sort(__m256i a[9]) //частично сортирует весь массив
{
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]);
Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]);
Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]);
Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]);
Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]);
Sort(a[4], a[2]);
}
void MedianFilter(const uint8_t * src, size_t srcStride, size_t width, size_t height, uint8_t * dst, size_t dstStride)
{
__m256i a[9];
for(size_t y = 0; y < height; ++y)
{
for(size_t x = 0; x < width; x += sizeof(__m256i))
{
Load(src + x, srcStride, a);
Sort(a);
_mm256_storeu_si256((__m256i*)(dst + x), a[4]); //сохранение 256 битного вектора по невыровненному по 32 битной границе адресу
}
src += srcStride;
dst += dstStride;
}
}
Примечание: Для получения максимального ускорения от оптимизации код, который содержит AVX2 инструкции, должен быть собран с следующими опцией компилятора: (/arch:AVX для Visual Studio 2012, -march=core-avx2 для GCC). Кроме того, очень желательно, чтобы в коде не было чередования AVX2 и SSE2 инструкций, так как переключение режима работы процессора в этом случае будет отрицательно сказывается на общей производительности. Исходя из выше сказанного, целесообразно располагать AVX2 и SSE2 версии алгоритмов в разных ".cpp" файлах.
Тестирование
Тестирование производилось на серых изображениях размером 2 MB (1920 x 1080). Для повышения точности измерения времени, тесты прогонялись несколько раз. Время выполнения получали делением общего времени исполнения тестов на количество прогонов. Количество прогонов выбиралось таким образом, что общее время исполнения было не меньше 1 секунды, что должно обеспечить два знака точности при измерении времени исполнения алгоритмов. Алгоритмы были скомпилированы с максимальной оптимизацией под 64 bit Windows 7 на Microsoft Visual Studio 2012 и запущены на процессоре iCore-7 4770 (3.4 GHz).
| Время выполнения, мс | Относительное ускорение | ||||
| Лучший скалярный | SSE2 | AVX2 | Лучший скалярный / SSE2 | Лучший скалярный / AVX2 | SSE2 / AVX2 |
| 24.814 | 0.565 | 0.424 | 43.920 | 58.566 | 1.333 |
Заключение
Как видно из результата тестов, ускорение алгоритма медианной фильтрации от использования SIMD инструкций на современных процессорах может достигать от 40 до 60 раз. Как мне кажется это достаточная величина, чтобы заморачиваться оптимизацией (если конечно в вашей программе важна скорость исполнения). В данной публикации я постарался максимально упростить используемый код.
Так за рамками остались вопросы, связанные выравниванием данных, с обработкой граничных точек, а также многое другое.
Данные вопросы я постараюсь раскрыть в следующих статьях. Если читателя интересует, как будет выглядеть боевой код, реализующий данную функциональность, то он сможет найти его здесь.
Автор: ErmIg






