Вступление
Вообще, речь пойдёт не о классической гомоку, а о русской вариации «пять в ряд». У вас есть листок бумаги в клеточку. Правила игры такие же, как в крестиках-ноликах. Отличие лишь в том, что необходимо выстроить линию из 5 элементов.
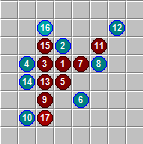
За такой нехитрой игрой мы прослушали не одну лекцию. Меня всегда раздражало, что моя блестящая стратегия разбивается о собственную невнимательность. Ну ничего, думал я, вот напишу программу, которая не будет делать ошибок, я тогда всем им покажу! Раз плюнуть! Пару циклов, правда, надо повозиться с пользовательским интерфейсом, но за пару вечеров управлюсь. С момента окончания института прошло 10 лет, а программу я всё ещё не написал.
Перебор в лоб
Идея состоит в том, что у нас нет никакой функции оценки, никакой эвристики. Мы просто расставляем элементы на поле, пока не достигнем пяти в линию. Сразу становится понятно, что такой метод не годится. Каждый ход в среднем генерирует 80 новых позиций. К 6 ходам количество вариантов возрастает до 80^6= 2^37 вариантов, что чересчур много.
Альфа-бета отсечение
Альфа-бета отсечение — это то, чем обычно ограничивается курс теории игр в институте. Применяется… честно говоря сложно придумать игру, в которой его можно применить. Возникает идея использовать функцию оценки в качестве критерия стоимости. Проблема в том, что нас по-настоящему интересует только победа или поражение. И нас вполне устроит победа за большее число шагов. Отсюда выплывает важное свойство: чтобы доказать победу с определённой позиции, достаточно найти один ход, а чтобы доказать поражение, необходимо перебрать все возможные ходы.
Решение с конца
Идея состоит в том, чтобы распознавать шаблоны, которые ведут к победе. Аналогия с шахматными программами — база эндшпилей.

Если вернуться на два шага назад, получим:

Линии можно комбинировать:
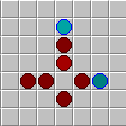
Весь набор комбинаций можно собрать в дерево поиска, которое разворачивается вокруг точки поиска.
Такое решение было реализовано, но работало медленно. Настолько медленно, что я так и не смог отладить код. Проблема в большом количестве комбинаций. Два шага назад — это всё, что ещё можно хранить в памяти.
Вычисление vs. хранение
После такого фейла я решил не хранить готовые шаблоны, а находить линии за один-два хода до победы «на лету». На удивление, это работало довольно неплохо. Вывод: иногда лучше решать, чем хранить.
В целях оптимизации я ограничил число возможных ходов двумя соседними клетками вокруг существующих. В общем-то, далеко не факт, что эффективные ходы ограничиваются этими клетками, но пока моё предположение неплохо согласуется с практикой.
В глубину или в ширину
Поиск в глубину предпочтительнее c точки зрения памяти, но часто уходит слишком глубоко, хотя победа находится рядом в соседней ветке. Поиск в ширину лишён этого недостатка, но требует много памяти для хранения уже решённых позиций. Обычно применяют форсированный поиск в глубину: поиск спускается на фиксированную глубину, но для перспективных позиций глубина увеличивается.
Оценочная функция
Скорость поиска очень чувствительна к порядку обхода. Для этого вводят функцию, которая оценивает «привлекательность» ходов и упорядочивает их по критерию такой привлекательности.
Открытая четвёрка. Гарантированная победа, если противник не выигрывает на следующем ходу.

Закрытая четвёрка. Один ход до победы.

Открытая тройка. Два хода до победы.

Приоритет линий в таком порядке. Оценка хода увеличивается, если в одной точке сходятся несколько линий разных направлений. Также учитываются линии противника и защитные ходы на них.
Работает довольно хорошо. Программа играет на уровне новичка. Это 2 уровня поиска в ширину и 3 уровня форсированного поиска в глубину. К сожалению, этого совершенно недостаточно, чтобы выигрывать всегда. На этом идеи у меня закончились, и я уже было думал, что ничего существенно улучшить не получится. Если бы я не наткнулся на работу некоего Louis Victor Allis.
Mr. Allis и Treat-Space search
В 1992г. мистер Алис (Allis), используя 10 рабочих станций SUN SPARC, доказал для классического гомоку с полем 15X15, что крестики всегда побеждают. Станции имели 64 и 128MB RAM, 200MB свопа. Т.к. они использовали станции Vrije Universiteit в Амстердаме, их процессы запускались только ночью. Процессы, которые не завершились за ночь, на утро убивались. На всё ушло 1000 CPU/часов и неделя времени.
- Расходящейся (diverging) называют игру, в которой количество возможных позиций растёт с увеличением числа фигур на доске.
- Под полной информацией (perfect-information) понимается то, что обоим противникам целиком всё известно о текущем состоянии игры. Примеры игр с полной информацией: шашки, шахматы. Примеры игр с неполной информацией (imperfect-information) дурак, преферанс.
- Внезапная смерть (sudden death) означает, что игра может внезапно закончится, когда ещё есть фигуры на доске или есть свободное пространство. Шахматы — пример игры с внезапной смертью. Игра, где этого не происходит — шашки.
Верхняя граница количества состояний (state-space complexity) 3225 ~= 10105. 1070 — сложность дерева решений (game-tree complexity)) при наличии предположения, что в среднем игра длится 30 ходов и имеет 225 — i возможных ходов на i-ом ходу.
Наблюдая за профессиональными игроками, Алис сделал вывод, что человек в первую очередь ищет цепочку угроз (threat sequence), которая может привести к победе. При этом ответные ходы противника практически полностью игнорируются. Только если подходящая цепочка найдена, проверяется возможность контратаки.
На этом факте и построена эвристика Treat-Space search. Для каждой атакующей линии с клеткой атаки (gain), которая базируется на уже существующих ходах (rest squares), мы отвечаем сразу всеми защитными ходами (cost squares). После этого проверяем, возможно ли ещё построить цепочку угроз, которая ведёт к победе.
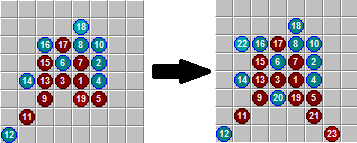
Начало цепочки угроз и её развитие
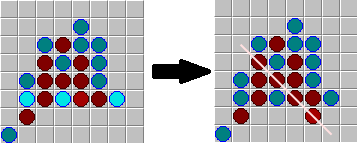
Анализ цепочки угроз. На первую угрозу, отвечаем сразу тремя защитными ходами. Несмотря на ответные ходы, возможно построение открытой четвёрки.
Такая эвристика позволяет нам эффективно искать цепочки угроз, на которые противник уже не в состоянии повлиять. Ответ одновременно всеми защитными ходами позволяет сделать сложность поиска практически линейной, а не комбинаторной. Конечно, каждую цепочку необходимо проверять на возможность контратак.
К сожалению, как проверять цепочки на возможность контратаки, я нифига не понял автор не уточнил. Поэтому пришлось лепить своё решение на коленке. На данный момент это самое медленное и стрёмное место в расчёте.
Эвристика нулевого хода
Лучше всего описана здесь.
Идея сводится к тому, что вы пропускаете свой ход, позволяя противнику сделать ход. Если ваша позиция всё ещё остаётся сильной, то, вероятно, данное состояние — не то, в которое противник позволит вам попасть. Это позволяет сэкономить один ход в глубину при анализе.
К сожалению, я не придумал как это безопасно и эффективно применить, поэтому пока не применяю.
Крестики выигрывают и дерево решений
С Treat-Space search эвристикой программа играет довольно сильно, но всё равно проигрывает сильному игроку. Это происходит потому, что программа способна «видеть» на 4 — 16 ходов вперёд. Иногда, особенно вначале партии, выгоднее ставить ходы на перспективу, а не пытаться развить локальное преимущество. Человек использует свой опыт, чтобы видеть направления, которые дадут преимущество в далёкой перспективе.
Так мы подходим к ещё одной проблеме компьютерных программ — недостаток опыта (lack of experience). Чтобы компенсировать это, в шахматных программах используется база дебютов. Можно подобное сделать игры «Пять в ряд». Проблема в том, что теорию гомоку я не осилил что теория для этой игры не так хорошо проработана, как для шахмат.
Поэтому возникает естественное желание перебрать дерево решений целиком, чтобы найти лучшие ходы. Как бонус можно получить доказательство, что крестики выигрывают, и оптимальную последовательность как бонус. Собственно это и сделал профессор Алис в своём исследовании.
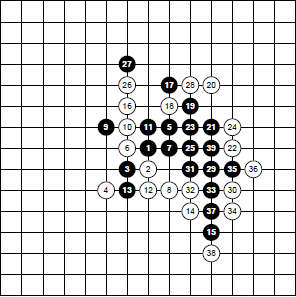
Наиболее длинная цепочка при совершенной игре для гомоку без ограничений
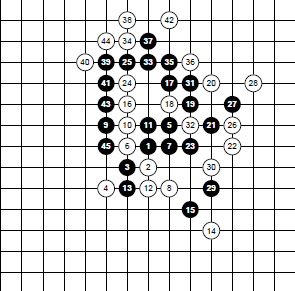
Наиболее длинная цепочка при совершенной игре для гомоку с ограничениями
Согласно теории, поле 19X19 даёт крестикам большее преимущество, чем 15X15, поэтому для неограниченного поля всё должно быть ещё легче.
Распределённые вычисления на коленке
Сразу становится понятно, что на одной машине такое не посчитать. С другой стороны, задача очень хорошо параллелится.
Пришлось повозится с базой, её размер предполагался очень большим и доступ к элементам происходит очень часто. У меня был существенный опыт с PostgreSQL, но она меня не устроила, поскольку, даже если данные умещаются в тоже место на диске, данная СУБД всё равно размещает их в конце таблицы из-за транзакционности. Таким образом, если один элемент изменяется часто, то таблица быстро распухает. Надо её вакумить, а на нагруженном сервере это проблематично. Вместо этого я родил свой велосипед, в котором в качестве базы использовался микс из AVL-дерева и структуры каталогов. Когда дерево превышает некий предел, оно разделяется на два в разных директориях. Получается такое себе хешодерево. На практике это оказалось плохим решением. Во-первых, AVL дерево — неудачный выбор, для работы с диском. В момент разделения данные поступают в новое дерево в сортированном порядке — это худший вариант для балансировки. Во-вторых, практика показала, что аккумулировать такое количество вычислительных ресурсов, чтобы база стала узким местом, довольно проблематично, и PostgeSQL меня бы целиком устроил.
В качестве вычислительных узлов, я планировал использовать «дешёвые» облачные сервисы. Я использовал и Scalaxy, и Amazon. Внезапно я осознал, что вычисления стоят реальных денег. Scalaxy давал 16 ядер на сервер, это обходилось мне, кажется, в 10$/сутки. При этом 16 процессов работали как-то очень натужно. На Амазоне я пытался пускать 2 инстанса по 8 ядер, и это тоже обходилось в существенную сумму. Также я пытался взять количеством и пустить 50 микроинстансов, что обошлось мне 40$ в сутки. По моим ощущениям, работали они хуже, чем 2 сервака по 8 ядер. Это заставило меня задуматься, сколько же в действительности стоят вычисления. На тот момент, мне требовалось 10000 ядер. Допустим, железо нам досталось бесплатно. Допустим, у нас 2-х процессорные 8-ядерные Xeon, с гипертрейдингом. Итого нам требуется 10000/(2*8*2)=312.5 серверов. Допустим такой сервер жрёт 200Вт. Итого в сутки нам надо оплатить 312.5*200Вт*24ч=1.5МВт*ч *0.11875$/(Квт/ч)= 178.125$/сутки.
Поэтому я
Как я заметил, на частных машинах расчёт идёт гораздо быстрее, чем на аналогичных по конфигурации виртуальных серверах. Так что, похоже,
Предвидя вопрос, почему я не использовал BOINC, отвечу так: мне просто неудобно лезть туда со своим проектом. Люди ищут лекарство от рака, ищут бозон Хигса, и тут я с какой-то непонятной задачей.
Согласно теории, к-во вариантов сначала расширяется, потом начинает сужаться за счёт отсечения решённых веток. Считалась позиция с 7 хода. Расчёт был на то, что к 8 ходу рост числа вариантов если и не уменьшится, то хотя бы замедлится скорость этого роста.
Расчёт продлился около месяца. К сожалению, чуда не произошло. К-во вариантов стабильно росло. Расчёт пришлось остановить. Даже на состояниях с 17-35 ходами дерево решений также стабильно расширяется.
Причина этого кроется в поиске в ширину. Мы затевали поиск в ширину, чтобы найти неочевидные решения.

Для этого приходится обходить все варианты, даже самые идиотские.
Алгоритм муравьиной колонии
Идеи у меня закончились, и я забросил проект почти на год, пока мой коллега не предложил мне использовать алгоритм муравьиной колонии.
Идея состоит в том, что мы случайным образом выбираем путь, который мы будет исследовать с определённого состояния. Вероятность хода зависит от соотношения числа побед/поражений всех потомков данной ветки.
Работает довольно неплохо. Проблема только в том, что нас не интересует, насколько вероятен проигрыш противника, если есть хотя бы одна позиция, в которой он может выиграть.
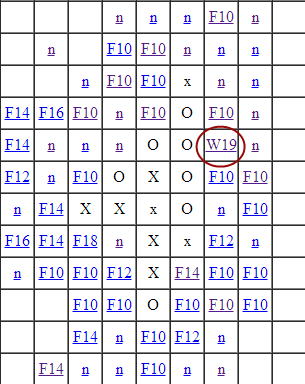
Спроси соседа про победу
Честно говоря, я не знаю, как называется эта эвристика. Она базируется на том факте, что для многих случаев ответные ходы противника не могут существенно повлиять на выигрыш.
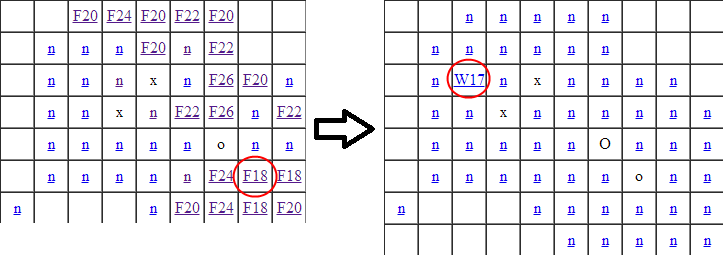
Мы делаем «перспективный» ход ноликом. Вскоре обнаруживаем, что он ведёт к поражению за 17 ходов
Делаем очередной «перспективный» ход ноликом из этого же состояния. Обнаруживаем, что крестики снова выигрывают, причём тем же ходом
Для разных ходов ноликом, у нас один и тот же ответный ход крестиком. Можно просто увеличить вес уже известным победным ходам, чтобы сократить число перебираемых ходов.
Эта эвристика, в совокупности с алгоритмом муравьиной колонии, даёт огромной прирост производительности. Она настолько эффективна, что за день работы находит решённые позиции, начиная с четвёртого хода.
База дебютов и человек
Если мы хотим доказать, что крестики начинают и выигрывают, нам достаточно сделать один идеальный ход крестиком, на каждый возможный ход ноликом. Это эквивалентно уменьшению общей глубины поиска в два раза. В некоторых случаях, как на картинке выше, идеальные ходы очевидны для человека.
Я планирую добавить возможность избирательно форсировать вычисление определённых веток в надежде на то, что это даст мне существенный прирост в производительности.
А давайте перепишем на ассемблер
Ни в одном проекте я не пытался сделать столько оптимизаций и не испытывал столько разочарования.
Факты неумолимы: константа не имеет никакого значения по сравнению с общей сложностью алгоритма. Напомню, каждая позиция в среднем даёт 80 новых позиций. Чтобы продвинуться на один шаг вглубь, мы должны увеличить скорость работы программы в 80 раз!!!
Итак, выборочный список того, что я предпринял:
- Инкрементальный поиск эффективных пустых клеток. При углублении поиска, добавляются только пустые клетки вокруг последнего хода. Для этого мне пришлось ввести состояния поля по глубине и довольно много кода для их поддержки.
- Там, где это возможно, я делал массивы типа std::vector<> статическими, чтобы избежать постоянного выделения памяти под такие массивы.
- Чтобы избежать постоянного выделения памяти под узлы дерева, счётчики ссылок для shared_ptr-узлов и полей внутри структур, реализующих эти узлы, я реализовал пул узлов. Чтобы ничего не поломать, этим пулом узлов приходилось очень аккуратно пользоваться. Никакой прирост производительности при этом вообще не обнаружился, и с огромной радостью я смог выкосить этот код.
Путём невероятных ухищрений и усложнения кода мне удалось увеличить скорость в 2.5 раза. Чувствуете разницу между ускорением в 2.5 раза и в 80 раз?
Часто предлагают делать расчёт на видеокарте с помощью CUDA. Проблема в том, что графические процессоры построены на SIMD архитектуре, и они очень не любят ветвления, а ветвления — это, фактически, способ работы поиска по дереву. Единственное, для чего их можно применить, — это поиск угрожающих линий с одной или нескольких позиций одновременно. Практический эффект от этого пока что сомнительный.
Хотя алгоритмическая оптимизация себя ещё не исчерпала. И вполне возможно, что для задачи такой сложности достаточно одного современного смартфона.
Так что алгоритмы рулят!
Благодарности
Я благодарен д-ру Louis Victor Allis за его умение решать нерешаемые задачи.
Я безмерно благодарен всем тем людям из сообщества RSDN, которые помогали и продолжают помогать мне обсчитывать эту задачу, используя свои ресурсы.
Я благодарен Рустаму за идею с алгоритмом муравьиной колонии.
Я благодарен Ване за стилистическую и орфографическую корректировку статьи. Надеюсь, я ничего не пропустил из твоих правок.
Ссылки и литература
Computer Chess Programming Theory
Knuth D. E., Moore R. W. An Analysis of Alpha-Beta Priming
Allis, L. V. (1994). Searching for solutions in games and artificial intelligence, Ph.D. Thesis, University of Limburg, Maastricht.
Allis, L. V., Herik, H. J. van den, and Huntjens, M. P. H. Go-Moku and Threat-Space Search
GORKOFF Об ИИ в интеллектуальных играх
Latobco Некоторые идеи написания искуственного интелекта для шахмат
Исходный код проекта
Сайт проекта
Автор: shebeko






