Линейное представление октодерева с использованием кода Мортона

Октодеревом называют древовидную структуру данных, каждый узел которой имеет восемь потомков. Октодеревья применяются для пространственной индексации, обнаружения столкновений в трехмерном пространстве, определения скрытых поверхностей, в трассировке лучей и методе конечных элементов.

Октодерево может быть представлено в виде иерархической структуры данных или линейно.
В иерархической структуре данных имеется корень дерева, узлы и листья. Каждый узел хранит указатели на его потомков.
При линейном представлении указатели не используются — применяются различные способы кодирования элементов и хранятся только листья дерева.
Одним из наиболее распространенных и эффективных способов кодирования является применение кривой Лебега (Z-кривой) и применение кривой Гильберта.
Достоинством кривой Гильберта является ее непрерывность — соседние элементы расположены последовательно. Преимуществом Z-кривой является простота и скорость вычисления, поэтому она чаще применяется на практике.

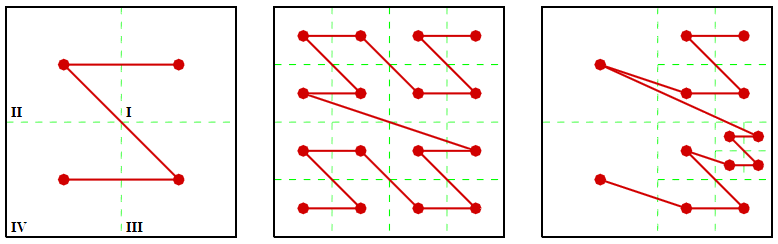
Двумерная кривая Лебега

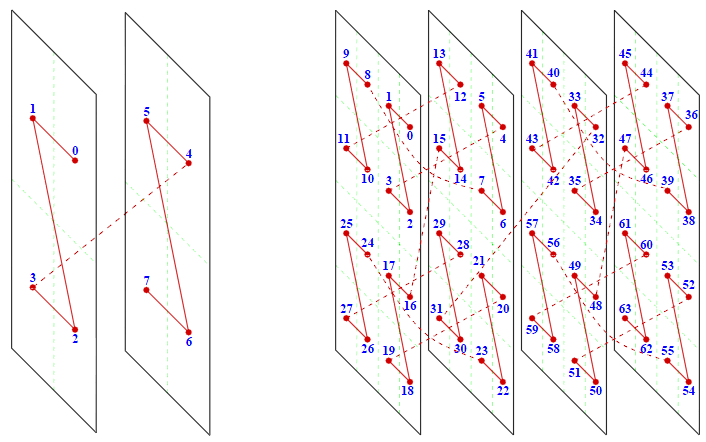
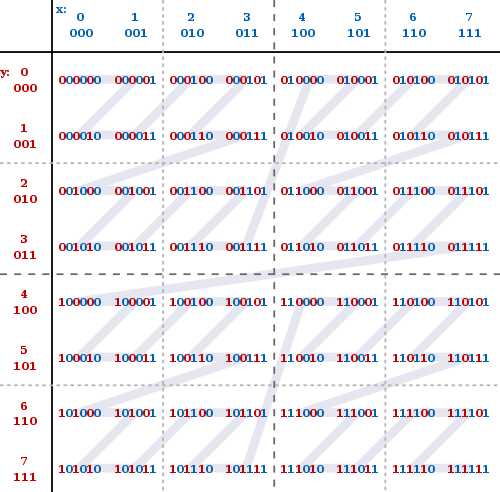
Трехмерная кривая Лебега

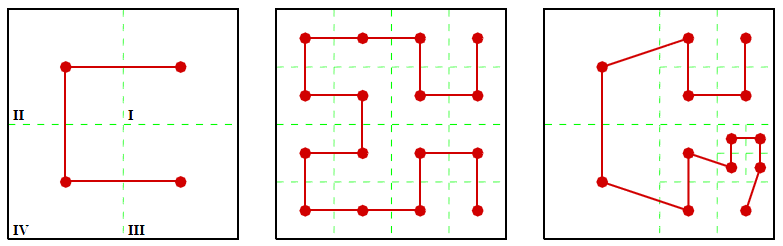
Двумерная кривая Гильберта

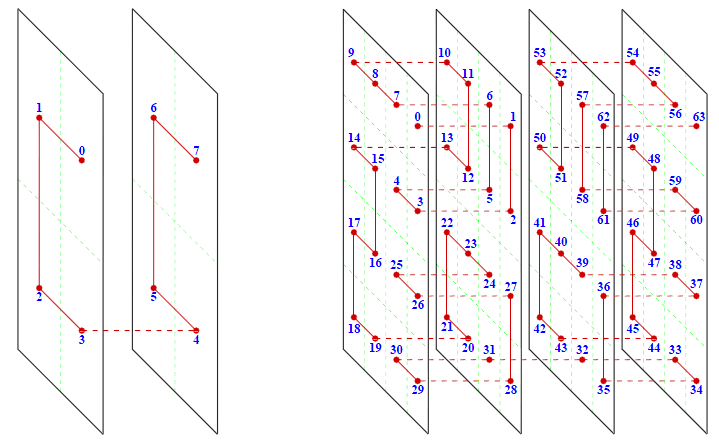
Трехмерная кривая Гильберта

Для кодирования элементов с использованием Z-кривой используется код Мортона(обычно код вычисляется для узла с минимальными координатами). Код Мортона для Z-кривой вычисляется смещением и смешиванием бит двоичного представления каждой из координат.

Пример вычисления кода Мортона

С учетом свойств Z-кривой, для элементов необходимо хранить только глубину элемента (уровень в октодреве) и его порядок (расположение на Z-кривой). В элементы используемого массива для хранения ячеек сетки заносятся значения глубины элемента, а индекс элемента определяет его расположение на Z-кривой.
Для хранения глубины элемента достаточно использовать 1 байт(глубина дерева 256). Для многих задач может оказаться достаточной глубина дерева 16(размер минимальной ячейки будет в 2^15 = 32768 раз меньше исходной области). Тогда для хранения ячейки достаточно использовать 4 бита.

Для определения вещественных координат элемента необходимо выполнить следующие шаги:
1. вычисление кода Мортона для элемента
2. декодирование
3. перевод полученного индекса в вещественное значение каждой из координат

Рассмотрим алгоритм на примере кодирования каждой из координат 20-тью битами, то есть результирующий код всех трех координат будет занимать 60 бит.
Зная код и глубину предыдущего элемента, можно вычислить код текущего элемента. Код первого элемента всегда равен 0. Определим смещение для каждого уровня глубины:

for ( unsigned char i = 0; i < 21; ++i ) {
  levelOffset[20 - i] = offset;
  offset *= 8;
}

Теперь будем определять индекс элемента через глубину и индекс предыдущего элемента:

unsigned long getElementIndex( const unsigned long prevIndex, const unsigned char prevLevel ) {
  return prevIndex + levelOffset[prevLevel];
}

Функция декодирования:

void decodeIndexXYZ( const unsigned long index, unsigned long iXYZ[3]) {
  iXYZ[0] = decodeIndex( index );
  iXYZ[1] = decodeIndex( index >> 1 );
  iXYZ[2] = decodeIndex( index >> 2 );
}

unsigned long decodeIndex( const unsigned long index ) {
  unsigned long ind = index & 0x0249249249249249;

  ind = ( ind | ( ind >> 2 ) ) & 0x00C9219243248649;
  ind = ( ind | ( ind >> 2 ) ) & 0x00386070C0E181C3;
  ind = ( ind | ( ind >> 4 ) ) & 0x0003E007C00F801F;
  ind = ( ind | ( ind >> 10 ) ) & 0x000000FFC00003FF;
  ind = ( ind | ( ind >> 20 ) ) & 0x00000000000FFFFF;

  return ind;
}

iXYZ[0], iXYZ[1], iXYZ[2] — определяют порядок кодирования(в данном случае сначала координата x, затем y, затем z).
Константы и количество шагов в функции decodeIndex определяются количеством бит и размерностью пространства(в данном примере константы приведены для трехмерного пространства и 20-ти бит на координату).
Существуют различные способы кодирования, примеры на
Bit Twiddling Hacks
How to compute a 3D Morton number (interleave the bits of 3 ints)

Для получения вещественных значений вершины ячейки с минимальными координатами, полученные индексы умножаются на величину шага. Величина шага — это размер минимальной допустимой ячейки сетки.
Размер ячейки можно определить по ее глубине. Остальные значения определяются прибавлением размера элементы к соответствующим минимальным координатам.

Деление элемента осуществляется путем увеличения его глубины и вставке после него 7 элементов этой же глубины.
Объединение — уменьшение глубины и удалении последующих 7 элементов.

Октодерево является активно изучаемой структурой данных и алгоритмы работы с ним(поиск соседей, интервалов, визуализация и тд) становятся темой докторских диссертаций и научных исследований.

Автор: lunserv

Источник