Как генерировать случайные скобочные последовательности

Привет!

При тестировании алгоритмов у меня часто возникает задача сгенерировать случайное бинарное дерево. Причем хотелка сводится не к абы какому случайному дереву, а взятому из равномерного распределения. Не смотря на кажущуюся простоту, эффективно построить такое дерево совсем нетривиально.

В названии этой статьи присутствуют слова «скобочная последовательность». За этими словами скрывается нечто большее, поскольку с помощью скобок можно описать очень разнообразные объекты, в том числе и бинарные деревья. На Хабре этому факту был посвящен отдельный пост.

В этой статье я расскажу несколько способов генерирования случайной скобочной последовательности, в том числе за линейное время, а потом приведу пример преобразования последовательности в бинарное дерево. Интересно?

Задача

По заданному n сгенерировать правильную скобочную последовательность согласно равномерному распределению над всеми правильными последовательностями длины 2n.

Инвентарь

Известно, что количество правильных скобочных последовательностей длины 2n равняется n-ому числу Каталана 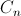. Для вычисления чисел Каталана cуществуют явные

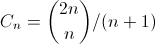
и рекурсивные

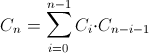
формулы.

Нам потребуется генератор случайных чисел. По заданному n, он будет генерировать равновероятно случайное число от 0 до 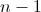. Также нам пригодится генератор случайных перестановок над списками. В питоне он называется random.shuffle. Нам будет достаточно того, что он работает линейное время и на последовательности 1,2,...,n генерирует случайную перестановку согласно равномерному распределению.

Три способа сказать «Авось»

Силы динамического программирования

Есть такая идея, что все правильные скобочные последовательности можно занумеровать. И, например, здесь есть подробное описание, как это делать. Значит, можно реализовать такой план.

• Считаем n-ое число Каталана.
• Генерируем случайный номер от 1 до .
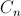• Силами динамического программирования и комбинаторного подсчета восстанавливаем скобочную последовательность по ее номеру.

План — почти отличный. Т.е. план совсем хорош, если n — маленькое, меньше 30. Но если n окажется порядка 1'000, потребуется длинная арифметика, алгоритмы по ссылке вместо обещанного квадрата будут работать кубическое время, и вообще, динамическое программирование — это вам не хухры-мухры. Я думаю, придется изрядно попотеть, чтобы уложиться с таким планом хотя бы в 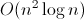. Давайте поищем альтернативные пути.

Попробуй и проверь

Взглянем еще раз на явную формулу для чисел Каталана.
.
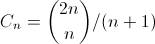На самом деле она означает, что правильных скобочных последовательностей очень много.

Будем называть последовательность сбалансированной, если число открывающихся и закрывающихся скобок в ней одинаково. Например, последовательности ")(()", "()()" являются сбалансированными, а последовательность "()))" — нет. Очевидно, что любая правильная последовательность является сбалансированной. Всего всех возможных сбалансированных последовательностей длины 2n существует 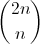. Если случайным образом выбрать одну из таких последовательностей, то она окажется правильной с вероятностью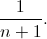

Новый план.

1. Генерируем случайную сбалансированную скобочную последовательность согласно равномерному распределению.
2. Проверяем ее на корректность.
3. Если последовательность правильная, то выводим. Если нет, то возвращаемся к пункту 1.

Начнем с первого пункта: как сгенерировать такую случайную скобочную последовательность. Давайте возьмем произвольную сбалансированную последовательность и перемешаем ее через random.shuffle.

	seq = ['(', ')'] * n
	random.shuffle(seq)

Если посидеть с бумажкой и ручкой, можно понять, что для любой сбалансированной скобочной последовательности x существует ровно 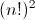перестановок, которые переводят произвольную начальную сбалансированную последовательность в x. Значит, random.shuffle генерирует любую сбалансированную последовательность с равной вероятностью. Получаем алгоритм.

def tryAndCheck(n):
	seq = [')', '('] * n
	while (not correct(seq)):
		random.shuffle(seq)
	return seq

Остается оценить время работы. Процедуры correct и random.shuffle работают за линию. Сколько будет итераций основного цикла? Нам известно, что правильная скобочная последовательность генерируется с вероятностью 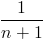. Тогда можно сказать, что у нас есть монетка, у которой орел выпадает с вероятностью 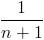. Нужно посчитать мат.ожидание числа бросков, пока не выпадет орел.

Как вариант, можно расписать мат.ожидание по формуле и получить что-то вроде такого:

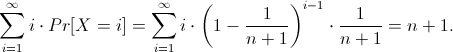
Или же воспользоваться общеизвестными фактами. Так или иначе, мат. ожидание времени работы всего алгоритма составит .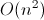

Попробуй и поправь

Хорошо, но что делать, если нам требуется действительно большая последовательность? Последовательность на миллион символов.

Линейный алгоритм уже не столь тривиален. В далеком 1992 году ему была посвящена отдельная статья Майка Аткинсона и Жоржа Сэка. Я изложу здесь свое видение на то, что написано в статье.

Нам потребуется волшебная функция f. На вход функция должна принимать сбалансированную скобочную последовательность, а на выход возвращать правильную той же длины. Важно, сделать так, чтобы функция раскидывала последовательности равномерно, а именно, на каждую правильную последовательность y приходилось ровно n+1 сбалансированная последовательность x, такая что f(x) = y. Если функцию можно посчитать за линейное время, то дело в шляпе.

Генерируем скобочную сбалансированную последовательность x согласно равномерному распределению и возвращаем f(x).

Вся хитрость в функции. Если хотите, можете остановиться и попробовать придумать такую самостоятельно. Не получается, ничего страшного. Сейчас я достану из цилиндра кролика из мира математики, и всем станет хорошо.

Пусть у нас есть счетчик, и изначально он равен нулю. Пробежимся по последовательности. За каждую открывающуюся скобку будем прибавлять очко, за каждую закрывающуся — вычитать.

balance = 0
for c in seq:
  balance += 1 if c == '(' else -1

График ниже отображает, как меняется счетчик balance по мере продвижения вдоль последовательности.

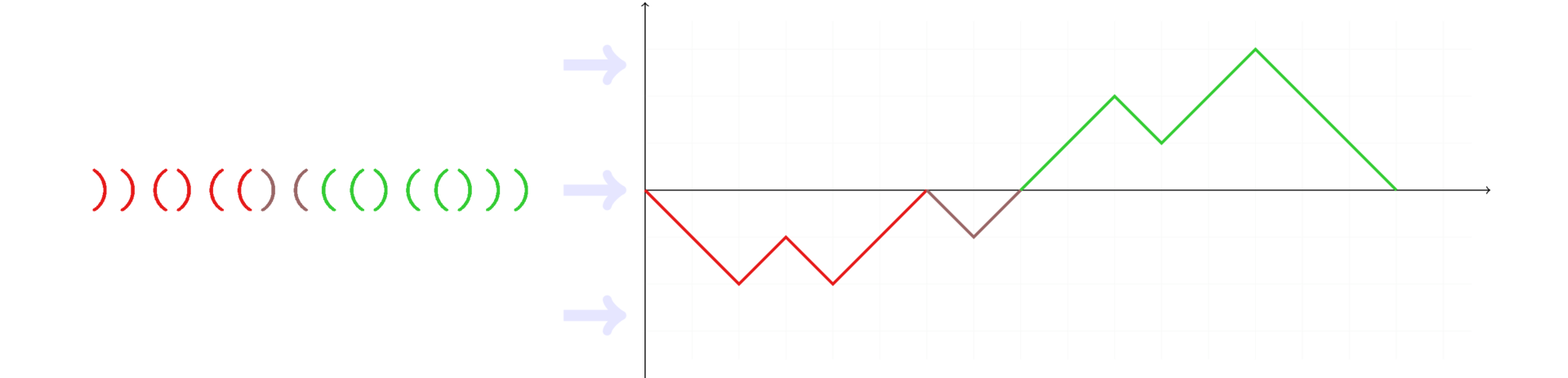
Последовательности, раскрашенные отдельными цветами, называются неразложимыми. Т.е. вообще последовательность неразложима, если счетчик на ней принимает нулевое значение только в начальной и конечной точке. Можно заметить, что неразложимые последовательности делятся на две категории: те, что целиком лежат выше нулевого уровня, и те, что ниже. Первые назовем положительными последовательностями, вторые — отрицательными.

Посчитаем суммарную длину отрицательных подпоследовательностей и поделим ее пополам. Полученная величина называется дефектом последовательности. У правильных последовательностей дефект нулевой. Если заменить все скобки в правильной последовательности длины 2n на обратные, дефект будет n.

Внимание, кролик! Теорема Чанга-Феллера. Число скобочных последовательностей длины 2n с дефектом k равняется n-ому числу Каталана 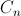и не зависит от k.

Теорема интересна тем, что разбивает все сбалансированные последовательности длины 2n на n+1 класс одинакового размера, и среди классов есть отдельный, содержащий все правильные скобочные последовательности. Значит, можно попробовать придумать функцию, которая бы каждую последовательность x с дефектом k кодировала бы правильной последовательностью y, и при этом по последовательности y и дефекту k можно было бы однозначно восстановить x.

Если удастся придумать такую функцию, то мы получим, что на каждую правильную последовательность приходиться ровно n + 1 сбалансированная с дефектами от 0 до n. Кажется, это просто.

Попытка 1.

Давайте все отрицательные подпоследовательности возьмем и инвертируем, т.е. заменим скобки на противоположные.

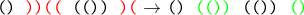
Плюс такой функции, она сохраняет позиции всех неразложимых последовательностей. Минус — теряем всю информацию о том, какая подпоследовательность была отрицательная, а какая — положительной. Даже зная, что дефект был 3, восстановить начальную последовательность из примера мы не сможем.

Попытка 2.

Давайте все отрицательные подпоследовательности инвертируем, а потом вынесем в конец.

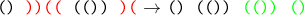
Теперь, зная дефект, мы можем восстановить отрицательные подпоследовательности. Но мы потеряли позции, где они находились.

Попытка 3.

Возьмем произвольную неразложимую отрицательную последовательность и оторвем у нее крайние скобки, а результат инвертируем.

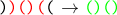
Такую операцию назовем хитрым инвертированием и обозначим через g. Поскольку последовательность неразложимая и отрицательная, результат будет всегда правильной скобочной последовательностью. Хитрость функции g в том, что с одной стороны она обратима, а с другой — у нас появились две лишние скобки, которыми можно кодировать позицию отрицательной подпоследовательности.

Допиливаем Попытку 2, только теперь выносим отрицательные последовательности в обратном порядке и хитро инвертируем их через функцию g:

Как видно из примера, позицию отрицательной подпоследовательности можно отметить освободившимися скобками. Я их выделил синим цветом и сделал квадратными. Буква e означает пустую последовательность.

Узнать, какие скобки зеленые, а какие синие можно по дефекту, а значит, можно востановить и саму начальную последовательность. Это то, что нужно!

Аткинсон и Сак предложили рекурсивную формулу для функции f:

Здесь 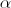неразложимая подпоследовательность, а — остаток.

Ниже я прилагаю реализацию алгоритма на Питоне с развернутой рекурсией. Несложно понять, что алгоритм работает линейное время.

def tryAndFix(n):
  seq  = ['(', ')'] * n
  random.shuffle(seq)

  stack   = []
  result  = []

  balance = 0
  prev    = 0
  for pos in range( len(seq) ):
    balance += 1 if seq[pos] == '(' else -1
    if balance == 0:
      if seq[prev] == '(':
        result.extend( seq[ prev : pos + 1 ] )
      else:
        result.append('(')
        stack.append( [ ')' if v == '(' else '(' for v in seq[ prev + 1 : pos ] ] )
      prev = pos + 1   

  for lst in reversed(stack):
    result.append(')')
    result.extend(lst)
  
  return result

Генерирование дерева

Если вы дочитали до этого места, я очень рад. Все, что осталось, преобразовать последовательность в дерево.

Скобочные последовательности длины 2n отлично кодируют деревья произвольной арности c n + 1 вершинами. Действительно, запустим поиск в глубину. При входе в вершину пишем открывающуюся скобку, на выходе — закрывающуюся.

В тоже время время деревья произвольной арности из n + 1 можно поставить во взаимно-однозначном соответствии с бинарными деревьями из n вершин. Все, что необходимо, сначала записать деревья произвольной арности в виде «левый ребенок — правый сосед», а затем переименовать правого соседа в правого ребенка.

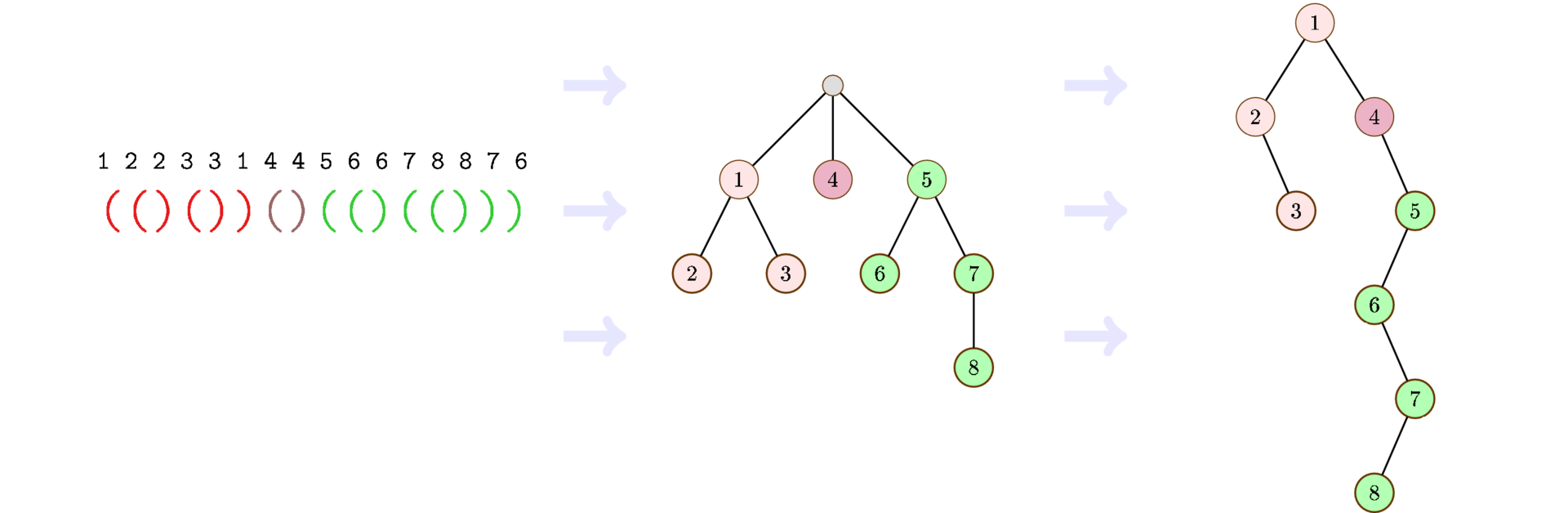
Спасибо, что были с нами!

Ссылки

• «Uniform Random Generation of Balanced Parenthesis Strings» D. B. Arnold, M. R. Sleep, 1980 — первая статья на тему генерации случайных скобочных последовательностей.
• «Generating binary trees at random» M. D. Atkinson, J.-R. Sack, 1992
• Скрипт на Пастбине

Автор: SeptiM

Источник