Способы представления словарей для автоматической обработки текстов

Автоматический анализ текстов практически всегда связан с работой со словарями. Они используются для морфологического анализа, выделения персон (нужны словари личных имен и фамилий) и организаций, а также других объектов.

В общем виде словарь — множество записей вида {строка, данные ассоциированные с этой строкой}.

Например, для морфологического анализа словарь состоит из троек {словоформа, нормальная форма, морфологические характеристики}. При анализе слова «мыла» из предложения «мама мыла раму» надо уметь получать следующие варианты анализа:

Нормальная форма	Характеристики
МЫЛО	S (существительное), РОД (родительный падеж), ЕД (единственное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫЛО	S (существительное), ИМ (именительный падеж), МН (множественное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫЛО	S (существительное), ВИН (винительный падеж), МН (множественное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫТЬ	V (глагол), ПРОШ (прошедшее время), ЕД (единственное число), ИЗЪЯВ (изъявительное наклонение), ЖЕН (женский род), НЕСОВ (несовершенный вид)

Хеш-таблицы

На первый взгляд все просто. Надо использовать хеш-таблицу и дело с концом. Когда словарь маленький это решение очень просто и эффективно.

Однако, например, морфологический словарь русского языка содержит около 5 млн. словоформ. Получается, что:

• Надо хранить эти 5 млн. словоформ
• Для каждой словоформы должна быть ссылка на множество наборов морфологических характеристик
• Для каждой словоформы хранить ее начальную форму

Такой способ организации данных является неэкономным, поскольку, во-первых, слова склоняются в основном регулярно, и, во-вторых, в случае русского языка в рамках одного словарной статьи можно выделить подгруппы словоформ, в которых сама форма изменяется незначительно, или не изменяется совсем.

Например, слово «стена»:

• ед. ч: «стена»[им], «стены»[род], «стене»[дат], «стену»[вин], «стеной»[твор], «стеною»[твор], «стене»[предл];
• мн. ч: «стены»[им], «стен»[род], «стенам»[дат], «стены»[вин], «стенами»[твор], «стенах»[предл].

Видно, что изменяется только окончание, но в хеш-таблице надо хранить слово целиком.

Можно раздельно храненить основы (неизменяемых частей) и окончания, но в этом случае усложняется проверка слова.

От префиксного дерева к конечным автоматам

Для ясности примеров будем рассматривать более простую задачу, когда для каждой словоформы при анализе надо получать только ее морфологические признаки. Как хранить нормальную форму будет описано в конце.

По сравнению с хеш-таблицами, более компактным представлением является префиксное дерево (trie):

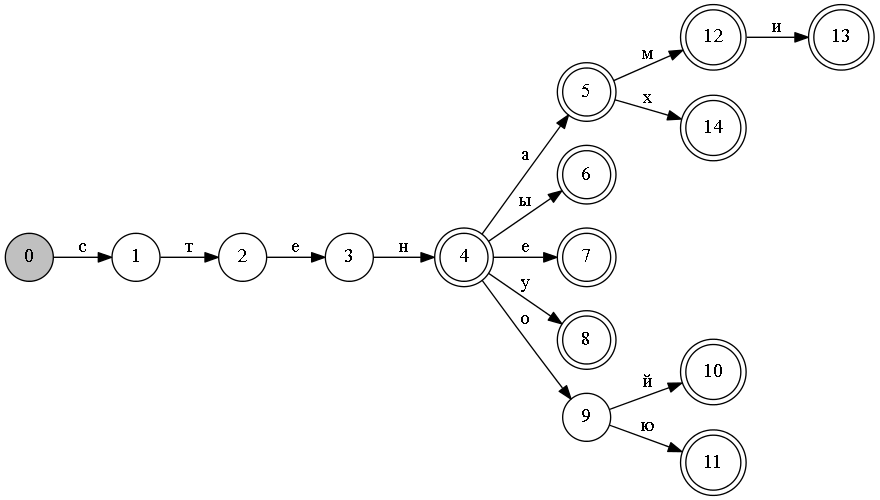
Важное замечание — на рисунках не будут показываться наборы признаков, ассоциированные с каждым конечным узлом дерева (или состоянием конечного автомата). Например, на рисунке узел 6, куда мы попадем по строке «стены» на самом деле будут 3 разбора:

• единственное число, родительный падеж;
• множественное число, именительный падеж.;
• множественное число, винительный падеж.

Префиксное дерево можно рассматривать как конечный автомат.

В автомате есть три вида состояний:

• Начальные — те, с которых начинается работа с автоматом. В детерминированном автомате такое состояние одно, но в недетерминированном их может быть несколько. На рисунках это крайнее левое состояние с номером 0.
• Финальные — такие состояния, достижение которых означает, что такое слово в словаре есть. Они обозначаются двойным кругом
• Простые состояния, которые не являются ни начальными, ни финальными

В дальнейшем будут использоваться обозначения:

• строка обозначается как w
• w[i] — i-тый символ данного слова (начиная с 0).
• s[i] — i-тый узел дерева (или состояние автомата), состояния нумеруются неотрицательными целыми числами, так же будем считать, что s[0] — начальное состояние.
• s[i][j] — переход из состояния s[i] по символу j. Считаем, что если переход есть, то такое выражение вернет номер состояния, если нет — то вернет -1.

Приведу базовые алгоритмы для префиксного дерева/конечного автомата.:

// вычислить префикс строки в автомате
// и вернуть последовательность (путь) состояний
int[] prefix(w) {
    int[] stateList;
    // сохраняем и начальное состояние в пути обхода префикса
    stateList[0] = 0;
    int current = 0;

    for(int i = 0; i < length(w); i++) {
        int next = s[current][w[i]]

        // если перехода нет, то выход
        if(next == -1)
            break;

        stateList[i+1] = next;
    }
    
    return stateList;
}

// добавить суффикс к заданному состоянию 
// и добавить состояния префикса к stateList
void addSuffix(w, int[] stateList) {
    // получить последнее состояние из пути обхода префикса
    int current = stateList[length(stateList) - 1];

    for(int i = length(stateList) - 1; i < length(w); i++) {
        // добавляем новое состояние в автомат
        int newState = addState();
        // добавить новый переход
        s[current][w[i]] = newState;
        current = newState;
        // сохраним состояние в пути обхода
        stateList[i + 1] = current;
    }

    // установка признака финальности для s[current]
    setFinal(current);
}

// добавить новую строку в trie
void add(w) {
    // найти максимальный общий префикс
    int[] prefixStates = prefix(w);
    // добавить оставшийся суффикс в автомат
    addSuffix(w, prefixStates)
}

Представление префиксного дерева как конечного автомата обладает важными свойствами:

• такой автомат детерминирован — из каждого состояния возможно не более одного перехода по некоторому символу
• в нем нет циклов — при любом способе обхода автомата никакое состояния не посещается более одного раза.

Такой специальный автомат называется DAFSA (deterministic acyclic finite state automaton).

Надо сделать еще одно важное замечание. Для удобства представления и для практического использования будем считать, что состояние описывается не только таблицей переходов, но и данными о финальности состояния. И будем считать, что состояние финально, если в нем такие данные есть, и нет — если они отсутствуют.

Минимальные конечные автоматы

Использование префиксных деревьев позволяет избавиться от избыточности префиксов. Фактически это означает, что сокращается объем для хранения неизменяемой части слова. Однако, например, в русском языке окончания слова изменяются в основном регулярно.

Например, слова «стрела» и «стена» изменяются одинаково:

СТЕНА: ед. ч: «стена»[им], «стены»[род], «стене»[дат], «стену»[вин], «стеной»[твор], «стеною»[твор], «стене»[предл]; мн. ч: «стены»[им], «стен»[род], «стенам»[дат], «стены»[вин], «стенами»[твор], «стенах»[предл].

СТРЕЛА: ед. ч: «стрела»[им], «стрелы»[род], «стреле»[дат], «стрелу»[вин], «стрелой»[твор], «стрелою»[твор], «стреле»[предл]; мн. ч: «стрелы»[им], «стрел»[род], «стрелам»[дат], «стрелы»[вин], «стрелами»[твор], «стрелах»[предл].

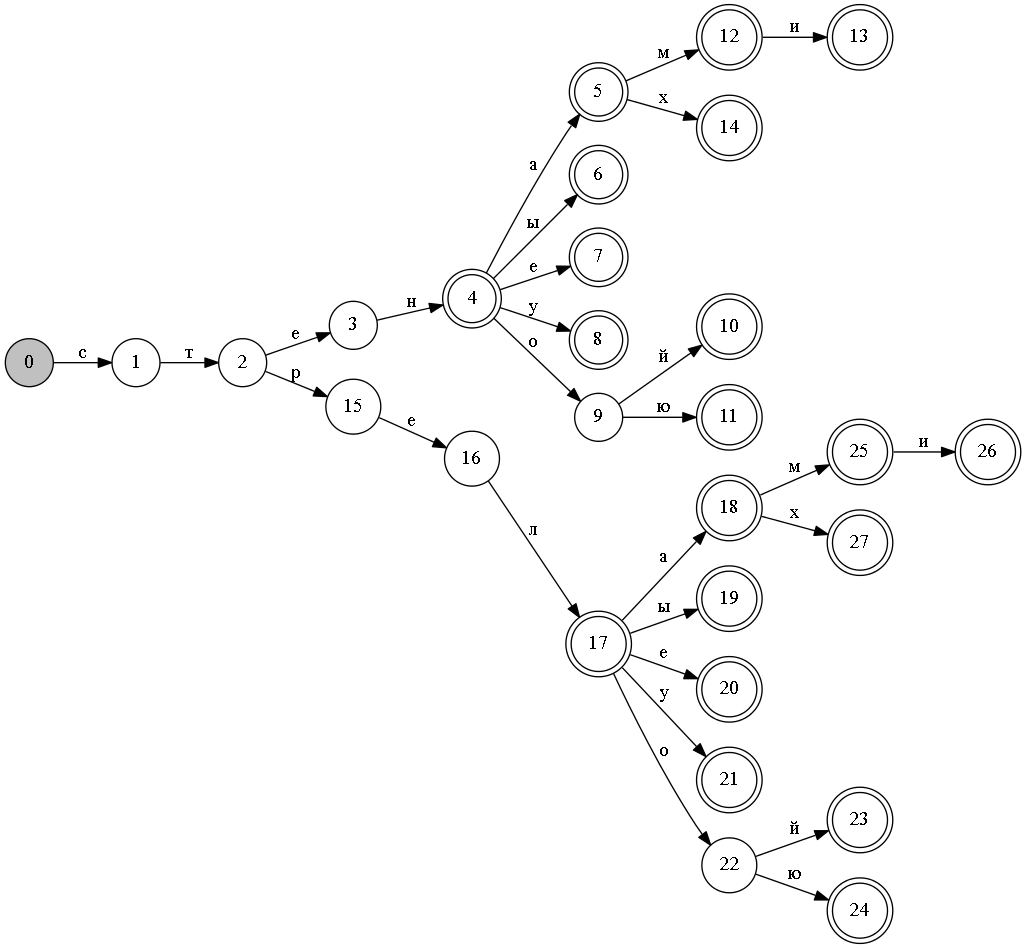
Видно, что состояния 4 и 17, с которых начинаются окончания, у обоих слов эквивалентны. Очевидно, что слов с одинаковыми правилами словоизменения в словаре будет много. А значит можно существенно сократить число состояний.

Собственно, в теории автоматов есть понятие о минимальном автомате – таком автомате, который содержит минимально возможное число состояний, но был бы эквивалентен данному.

Например, для приведенного выше автомата, минимальный выглядит вот так:

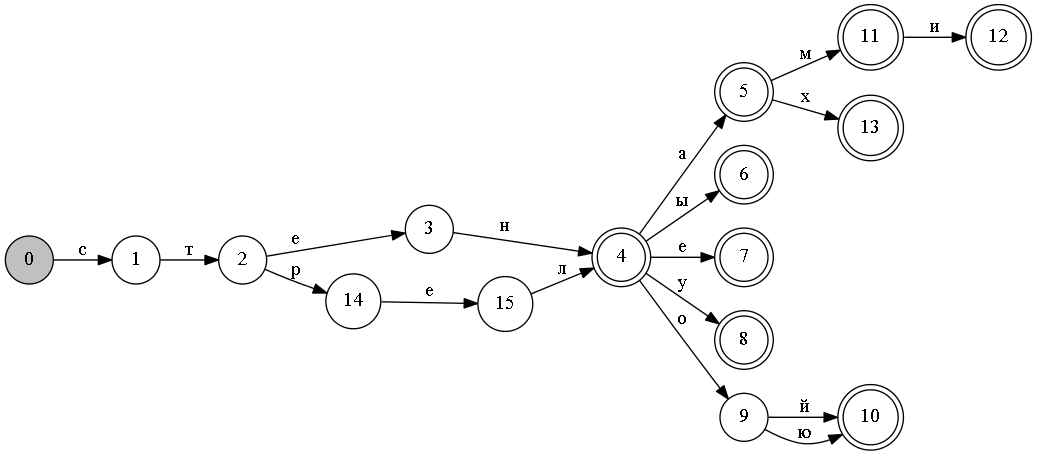
Существуют и алгоритмы минимизации конечных автоматов, но все они обладают существенным недостатком — для их работы необходимо построить сначала неминимизированный автомат.

Другим, менее очевидным недостатком, является то, что построенный минимальный автомат не так просто изменять. К нему не подходит простая процедура добавления нового слова, которая используется для префиксного дерева.

Например, мы построили автомат для слов «fox» и «box», а потом минимизировали его.

Если в этот автомат добавить без полного перестроения слово «foxes», то получится следующая картина:

Получается, что в месте с «foxes» добавилось и «boxes», которое мы не добавляли.

В результате схема использования классических алгоритмов минимизации следующая: при любом изменении словаря необходимо:

• Построить префиксное дерево (или дополнительно хранить)
• Минимизировать автомат

Если словарь большой, то эти процедуры могут занимать значительное время и объем памяти.

Инкрементальная минимизация детерминированных ацикличных конечных автоматов

Решение трудностей с минимизацией автоматов представлено в работе: Jan Daciuk; Bruce W. Watson; Stoyan Mihov; Richard E. Watson. «Incremental Construction of Minimal Acyclic Finite-State Automata». В ней представлен алгоритм инкрементальной минимизации детерминированных ацикличных конечных автоматов. Он позволяет изменять уже построенный минимальный автомат. В результате не надо строить полный автомат, а затем его минимизировать.

Опять рассмотрим наш автомат СТЕНА+СТРЕЛА:

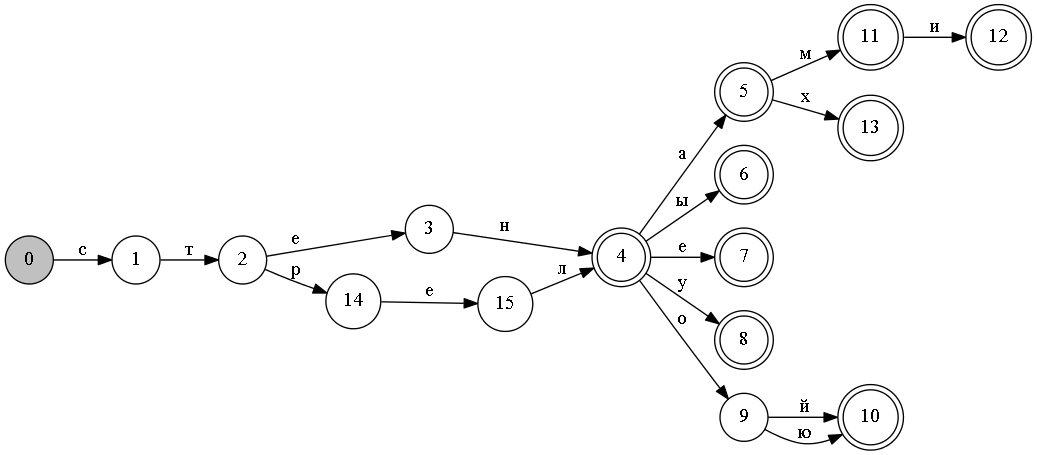
Важным понятием алгоритма является «состояния строки» — это последовательность состояний, которая получается при обходе автомата по заданной строке.

Например, при обходе строки «стрелой» получим следующую последовательность состояний [0, 1, 2, 14, 15, 4, 9, 10].

Другим важным понятием этого алгоритма является число переходов в заданное состояние (confluence). Если число переходов более одного, то изменять такое состояние небезопасно. На рисунке это состояние 4: у него 2 входящие стрелки.

Кроме того, алгоритм предполагает, что существует реестр состояний, который позволяет быстро получить состояние, равное данному.

В результате алгоритм добавления слова w выглядит так:

void addMinWord(w) {
    // найти максимальный префикс w и сохранить его состояния
    int[] stateList = commonPrefix(w); 

    // найти первое состояние с более одним входящим переходом
    int confIdx = findConfluence(stateList);

    // клонировать его и все последующие состояния
    if(confIdx > -1) {	
         int idx = confIdx;

        while(idx < length(stateList)) {
            int prev = stateList[idx - 1];
            int cloned = cloneState(stateList[idx]);
            stateList[idx] = cloned;
            // после клонирования самого состояния
            // нужно заменить переход с предыдущего на клонированное
            s[prev][w[idx - 1]] = cloned;
            idx++;
            confIdx++;
        }
    }
    // добавить суффикс
    addSuffix(w, stateList);

    // заменить состояния строки теми, что есть в реестре. 
    //Если их нет, то добавить в реестр
    replaceOrRegister(w, nodeList);
}

void replaceOrRegister(w, int[] stateList) {
    int stateIdx = length(stateList) - 1;
    int wordIdx = length(w) - 1;
    
    // обходим состояния строки с конца
    while(stateIdx > 0) {
        int state = stateList[stateIdx];
        // получить из реестра состояние, равное state
        int regState = registerGet(state); 

        if(regState == state) { 
                // если в реестре state уже есть, то переходим к предыдущему
                continue;  
            } else if(regState == -1) {
                // если состояния в реестре нет, то добавим его в реестр
                registerAdd(state);
            } else { 
                // основная часть, когда в реестре есть состояние, равное state
                int in = w[wordIdx];
                // корректируем переход
                s[stateList[stateIdx - 1]][in] = regState; 
                // заменяем состояние в пути обхода
                stateList[stateIdx] = regState; 
                // удаляем замененное состояние из автомата
                removeState(state);  
            }
        wordIdx--;
        stateIdx--;
    }
}

Иллюстрация работы алгоритма

Рассмотрим простой случай, когда финальность состояние — бинарный признак. Состояние или финально, или нет.

Автомат для строки «fox».

Видно, что автомат минимальный, в реестре находятся все состояния [0,1,2,3]

Добавим к нему слово «box». Поскольку у них нет общего префикса, то добавляем всю строку как суффикс. В результате получим:

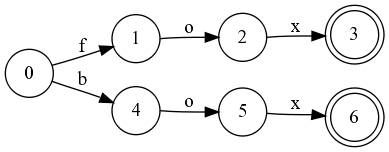
Можно заметить что состояния 3 и 6 равны. Заменим 6 на 3:

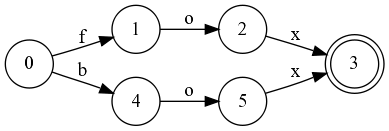
Теперь видно, что равны 2 и 5. Заменим 5 на 2:

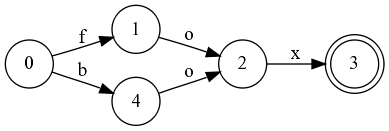
А теперь видно, что равны 1 и 4. Заменим 4 на 1:

Добавим строку «foxes». При вычислении префикса нашли, что состояния [0, 1, 2, 3] — путь префикса.
Кроме того, обнаружили, что в состояние 1 входит более одного перехода. Как результат — надо клонировать состояния 1, 2 и 3 по пути обхода слова «fox», поскольку если просто добавить «foxes» к предыдущему автомату, то будет распознаваться строка «boxes», которую мы не задавали.

Теперь добавим «boxes»:

При добавлении «boxes» автомат стал меньше. Это на первый взгляд неожиданное поведение, когда при добавлении новых строк автомат в действительности уменьшается. Есть и обратное поведение — когда при удалении строки автомат увеличивается.

Для правильной работы алгоритма важно корректно реализовать работу с реестром. Состояние удаляется из реестра при любом его изменении таблицы переходов состояния и признака финальности.

Кроме того, в отличие от обычного множества или таблицы, в добавление/удаление из реестра оперирует точно этим состоянием, а запрос делается на равное.

Практические использование

Представленный алгоритм используется в проекте АОТ и в системе ЭТАП-3 для организации быстрого морфологического анализа. При использовании конечных автоматов достигается скорость анализа порядка 1-1.5 млн. слов в секунду. При этом размер автомата без особых ухищрений умещается в 8 Мб.

Ранее описывалось хранение данных строки как признак финальности. Рассмотрим этот подход более подробно.

Хранение данных в состоянии автомата

Подход предполагает, что данные строки рассматриваются как некий атомарный объект. Это в свою очередь накладывает ограничения на эффективность минимизации автомата.

Например, процедура построения минимального автомата бессмысленна для идеального хеширования, когда со строкой ассоциировано уникальное число. Потому что в этом случае каждый суффикс будет уникальным, и соответственно, минимизации не будет, поскольку каждое финальное состояние уникально.

Для морфологического анализа в качестве ассоциированных данных можно использовать наборы морфологических характеристик. Это хорошо работает, поскольку таких наборов мало относительно общего количества словоформ. Например в русском языке в зависимости от принятой модели число таких наборов 500-900. А словоформ 4-5 млн.

Однако, эффективность минимизации сходит на нет, если в добавок к характеристикам сохранять и полную нормальную форму. Это происходит потому, что пара {нормальная форма, морфологические характеристики} практически уникальна.

В системе ЭТАП-3 используется именно такой подход для хранения морфологической информации. В самом автомате хранятся только наборы морфологических признаков. А для хранения нормальной формы используется следующий трюк. На этапе построения автомата в качестве входного символа используется не один знак, а два. Например, при добавлении словоформы «стеной» (СТЕНА в творительном падеже) будет добавлена следующая последовательность пар знаков: «с: С», «т: Т», «е: Е», «н: Н», «о: А», «й:_».

Все словоформы слов «стена» и «стрела» в таком автомате будут выглядеть так:

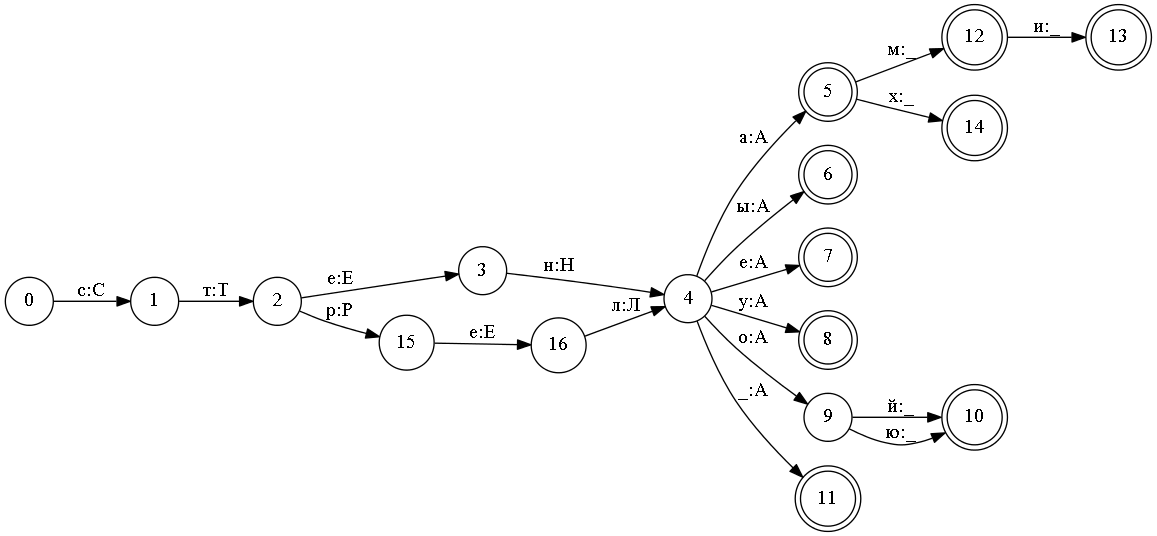
Такой подход к записи нормальной формы обладает важным достоинством. Он позволяет работать с морфологией в двух направлениях. Можно по словоформе получить ее разбор — анализ. А можно по нормальной форме получить все ее словоформы — синтез.

Недостатком такого подхода является то, что несмотря на то, что для пары знаков автомат является детерминированным, то для входного он уже не является таковым и надо перебирать все переходы из данного состояния. Например состояние m, на рисунке выше. В нем имеется несколько переходов по знаку словоформы «а».

Хранение данных в переходах. Использование аннотаций

Другой способ для хранения дополнительных данных был описан в оригинальной работе. Он предполагает изменение самих строк, которые хранятся в автомате.

Предлагается сделующая схема. Вместо целевой строки в автомат записывается расширенная строка, которая состоит из целевой строки, символа начала данных (аннотирующего символа) и самих данных.

Например, в этом случае морфологические характеристики могут быть записаны следующим образом: «стена|+сущ+жен+им, ...», где '|' — аннотирующий символ, а "+cущ", "+жен", "+им" — специальные символы данных.

Этот подход используется в системе АОТ. В ней в качестве данных хранится фактически две ссылки: на морфологические характеристики и на номер правила словоизменения. В результате при анализе можно по словоформе получить как ее морфологические признаки, так и начальную форму.

Особенностью этого подхода является то, что несколько усложняется модель автомата. Символ перехода интерпретируется по-разному в зависимости от того был он до аннотирующего символа или после.

Другой особенностью является то, что для обход по строке несколько усложняется. Во-первых, строка присутствует в автомате, если после ее обхода мы оказываемся в состоянии, из которого есть переход по аннотирующему символу. Во-вторых, необходима процедура сбора всех аннотаций после аннотирующего символа. В третьих, необходима процедура декодирования аннотации.

Оптимизация объема памяти

Для оптимизации объема памяти используется два представления конечных автоматов: один для построения минимального автомата, а другой — для анализа. Разница между ними в том, что автомат для анализа не предполагает изменений и поэтому может быть более эффективно размещен в памяти.

Автомат для анализа состоит из трех структур:

1. таблица переходов — пары целых {символ перехода, целевое состояние}
2. индексы начала и конца диапазона переходов состояния
3. таблица данных финальных состояний

Автоматы получаются достаточно компактными. Например, словарь АОТ без особых ухищрений занимает около 8Мб. Полные данные системы морфологического анализа, которые включают в себя не только анализ по словарю, но и предиктивный анализ слова умещаются в 16Мб.

Сами алгоритмы минимизации реализованы в моем проекте на Github: github.com/kzn/fsa

Автор: kzn

Источник