Дисклеймер: для понимания этой статьи требуются начальные знания теории графов, в частности знание поиска в глубину, поиска в ширину и алгоритма Беллмана — Форда.
Введение
Наверняка вы сталкивались с задачами, которые приходилось решать перебором. А если вы занимались олимпиадным программированием, то точно видели NP-полные задачи, которые никто не умеет решать за полиномиальное время. Такими задачами, например, является поиск пути максимальной длины без самопересечений в графе и многим известная игра — судоку, обобщенная на размер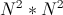 
. Полный перебор крайне долгий, ведь время его работы растёт экспоненциально относительно размера входных данных. Например, время поиска максимального пути в графе из 15 вершин наивным перебором становится заметным, а при 20 — очень долгим.
В этом посте я расскажу как можно оптимизировать большинство переборов, чтобы они стали работать на порядки быстрее.
Поподробнее про перебор
Пример
Рассмотрим наивное решение задачи о нахождении пути максимальной длины без самопересечений в графе G.
Запускаем немного измененный обход в глубину. А именно, вместо проверки на то, посетили ли мы вершину делаем проверку на принадлежность вершины к текущему пути. И теперь, если на каждой итерации обновлять текущий глобальный результат, то в итоге в этой переменной будет лежать ответ на задачу.
Если посмотреть в это решение чуть глубже, то можно увидеть, что по-настоящему был запущен классический поиск в глубину, но на другом графе — графе состояний S. В этом графе вершины задаются маской вершин графа G, принадлежащих текущему пути, и номером последней вершины. Рёбра задаются наличием ребра в графе G между последними вершинами путей и равенством остальной маски.
Большинство переборов можно представить в виде поиска по графу состояний.
А что мы собственно ищем
Переборы бывают трёх типов:
1) Проверка существования.
2) Максимизация/Минимизация на не взвешенном графе.
3) Максимизация/Минимизация на взвешенном графе.
Для решения наивным методом первых двух задач используется поиск в глубину или поиск в ширину, а для третьей — алгоритм Беллмана — Форда по графу состояний S.
А теперь сами оптимизации.
Оптимизация №1: меморизация, или ленивость
Не нужно делать одно и тоже несколько раз. Можно просто запомнить результат, и когда в следующий раз нужно будет сделать ту же работу, просто взять её результат. Это работает на задачах проверки существования, а на двух других это иногда работает частично. Есть два варианта: или результат состояния кодируется им же, или нет. Если да, то меморизация работает отлично. Если нет, то меморизация может помочь не делать работу, когда текущий ответ состояния хуже, чем был когда-то до этого момента в этом же состоянии.
Если граф состояний S мал, то нам повезло — можно сделать булевский массив, иначе меморизацию лучше всего реализовать хеш-таблицей.
Обычно реализовать это не сложно. Нужно добавить 2 строчки: в начале проверять, что нас здесь ещё не было, а в конце записывать, что мы здесь были.
Оптимизация №2: отсечение по ответу
Оптимизация заключается в том, что мы сравниваем оценку наилучшего ответа, достижимого из этого состояния, с текущим глобальным результатом. Эта оптимизация работает, если нам надо что-либо максимизировать или минимизировать. В случае проверки существования можно сделать оценку достижимости результата. Например, в проверке является ли граф гамильтоновым, можно добавить проверку достижимости всех вершин графа G, не проходя через вершины, лежащие на текущем пути.
Хорошим примером для этой оптимизации является поиск пути максимальной длины без самопересечений в графе G. Эта задача NP-полная.
Допустим, мы находимся в каком-то состоянии s графа S. Если нам, как ни крути, не удастся улучшить результат, то стоит вернуться. Теперь надо научиться это проверять. Например, можно посчитать количество достижимых вершин графа G из последней вершины пути состояния s и прибавить длину уже полученного пути, то полученное число будет верхней границей максимального ответа, достижимого из s. Значит, если оно меньше текущего результата, то можно не запускать перебор из этого состояния.
Если абстрагироваться от конкретной задачи, то надо подобрать такую функцию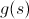 
, чтобы 
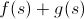было оценкой ответа достижимого из s, где 
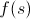— это текущий ответ состояния s.
Если функция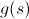 
будет достаточно хорошо отражать реальность, то эта оптимизация может ускорить работу алгоритма на порядки.
Отсечение по ответу, пожалуй, самая важная оптимизация, потому что её используют многие другие оптимизации и методы.
Оптимизация №3: жадность
Жадность — это когда мы хватаем всё самое, на первый взгляд, хорошее. То есть идём по ребру, которое нам показалось перспективней остальных. Проблема в том, что ответ, который находит жадность, необязательно самый хороший, но чем лучше наша оценка, тем лучше результат. За функцию оценки можно взять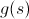 
из отсечения по ответу.
А теперь по порядку.
Отсечение по ответу срабатывает чаще, если есть хороший ответ. Тогда можно вначале запустить жадный алгоритм и получить какой-то ответ. Это будет неплохим началом, чтобы отсекать совсем плохие ветки перебора.
Посмотрим на работу поиска в глубину. В состоянии s мы перебираем рёбра в каком-то случайном порядке и запускаемся от них дальше. Так давайте перебирать рёбра в порядке убывания оценки 
. Для этого просто отсортируем их в поиске в глубину перед переходом в следующие состояния. Тогда отсечение по ответу будет сперва получать более качественные состояния. Стоит заметить, что в таком виде поиск в глубину в самом начале будет действовать как жадный алгоритм, значит отдельно его можно не запускать.
Пара слов про взвешенные графы
Обычно алгоритм Беллмана — Форда пишут примерно так:
for v in vertices:
for e in edges:
relaxation(e)
А можно его написать немного по-другому: как поиск в ширину, но при проверке на то, посетили ли мы раньше это состояние, сравнивать текущий и меморизированный, и, если меморизированный лучше, то отрубать эту ветку перебора.
Чем «плох» поиск в глубину и поиск в ширину
Немного картинок:
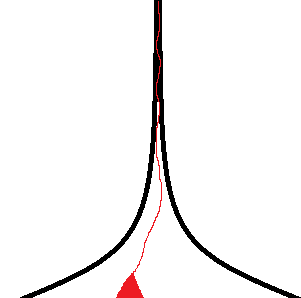
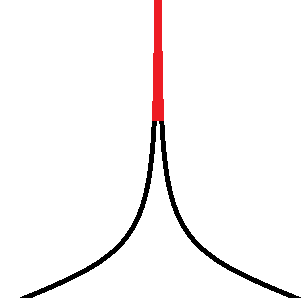
Красным выделены множества посещённых состояний графа S после некоторого времени работы поиска в глубину и в ширину соответственно.
Обе эти области очень сильно локализованы в каком-то одном месте. Нужен какой-то механизм, который будет распределять красную область по всему графу S, чтобы быстрее улучшать ответ, который поможет отрубать плохие ветки перебора.
Если мы решаем задачу минимизации, то действия поиска в ширину выглядят логично, но, к сожалению, он вряд ли получит какой-то ответ для отсечения.
Механизмы выбора области поиска
Жадность
И опять к нам пришла жадность, но теперь немного в другом ключе. В прошлый раз мы сортировали рёбра и переходили по ним всем последовательно, но это нам слабо поможет искать более глобально, чем на картинках сверху.
Все помнят, что есть число 1 и есть число N, но многие забывают, что есть ещё и числа между ними. Жадность — это выбор одного ребра, а поиск в глубину — выбор N рёбер. Давайте напишем жадный поиск в глубину, который будет переходить по первым k рёбер.
Если использовать этот метод, то перебор будет обходить намного большие поддеревья графа S.
Проблема в том, что если взять слишком маленькое k, то ответ может оказаться неправильным, а если слишком большое, то времени может не хватить. Решение довольно простое: надо выбрать все возможные k. То есть написать внешний цикл, перебирающий k от 1 до бесконечности, пока время не кончилось, а в теле цикла запускать поиск решения.
Здесь стоит понять, что так как количество просмотренных состояний графа S растёт экспоненциально относительно роста k, то перебор этой переменной от 1 до k-1 не будет увеличивать асимптотическую сложность. В худшем случае время работы увеличится не более чем в константу раз, а на практике значительно уменьшится из-за отсечения по хорошему ответу.
Iterative deepening
Этот метод как бы заставляет поиск в глубину выполнять не те задачи, которые он обычно выполняет.
Суть метода заключается в том, чтобы создать глобальную переменную — максимальная глубина, на которую должен спускаться поиск в глубину. Так же как и с k запускаем внешний цикл по этой глубине.
Теперь поиск в глубину больше напоминает поиск в ширину, но с той разницей, что он сразу получает какой-то ответ для отсечения.
Ограничение размера очереди поиска в ширину
Это тоже жадность, но теперь для поиска в ширину. Из названия понятно, что мы будем ограничивать очередь. Для этого опять заведём глобальную переменную — размер очереди и переберём её от 2 до бесконечности. Но перебирать будем не по +1, а умножать на константу, например, на 2.
В какой-то момент размер очереди превысит выбранный максимальный размер и придётся кого-то выбросить за борт. Чтобы выбрать, надо отсортировать по какому-то признаку. Будем использовать, как всегда, функцию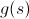 
для сравнения состояний.
Что из всего этого теперь писать
Для наилучшего результата надо написать почти всё и почти сразу.
Вначале запускаем поиск в глубину на некоторое время с меморизацией, отсечением по ответу, сортировкой рёбер, и перебором k, но без Iterative deepening.
Далее запускаем поиск в ширину с отсечением по ответу и ограничением размера очереди.
Поиск в глубину нужен, чтобы найти неплохой ответ для отсечения в поиске в ширину, а поиск в ширину нужен, чтобы найти уже наилучший ответ. Эта сборная солянка неплохо показывает себя во многих задачах на перебор.
Теперь немного практики
Поиск максимального пути без самопересечений в графе
Случайный граф: 18 вершин, 54 ребра.
Время работы:
Нет оптимизаций ~ 4 сек.
Меморизация, отсечение по ответу ~0.2 мс.
Случайный граф: 30 вершин, 90 рёбер.
Нет оптимизаций > 1 часа (не дождался).
Меморизация, отсечение по ответу ~ 0.5 с.
Меморизация, отсечение по ответу, жадность ~ 10 мс.
Автор: Frommi
