Булевы операции двумерных тел

В детстве меня всегда завараживали игры с динамическим ландшафтом: The Castle и Worms Armageddon. В то время я не понимал, как реализована эта удивительная механика разрушения и изменения мира. Позже я узнал, что секрет заключался в использовании растровой графики, но мне было интересно как реализовать тоже самое не прибегая к растру. В этой статье я хочу рассказать об одном из таких векторных решений.

Постановка задачи

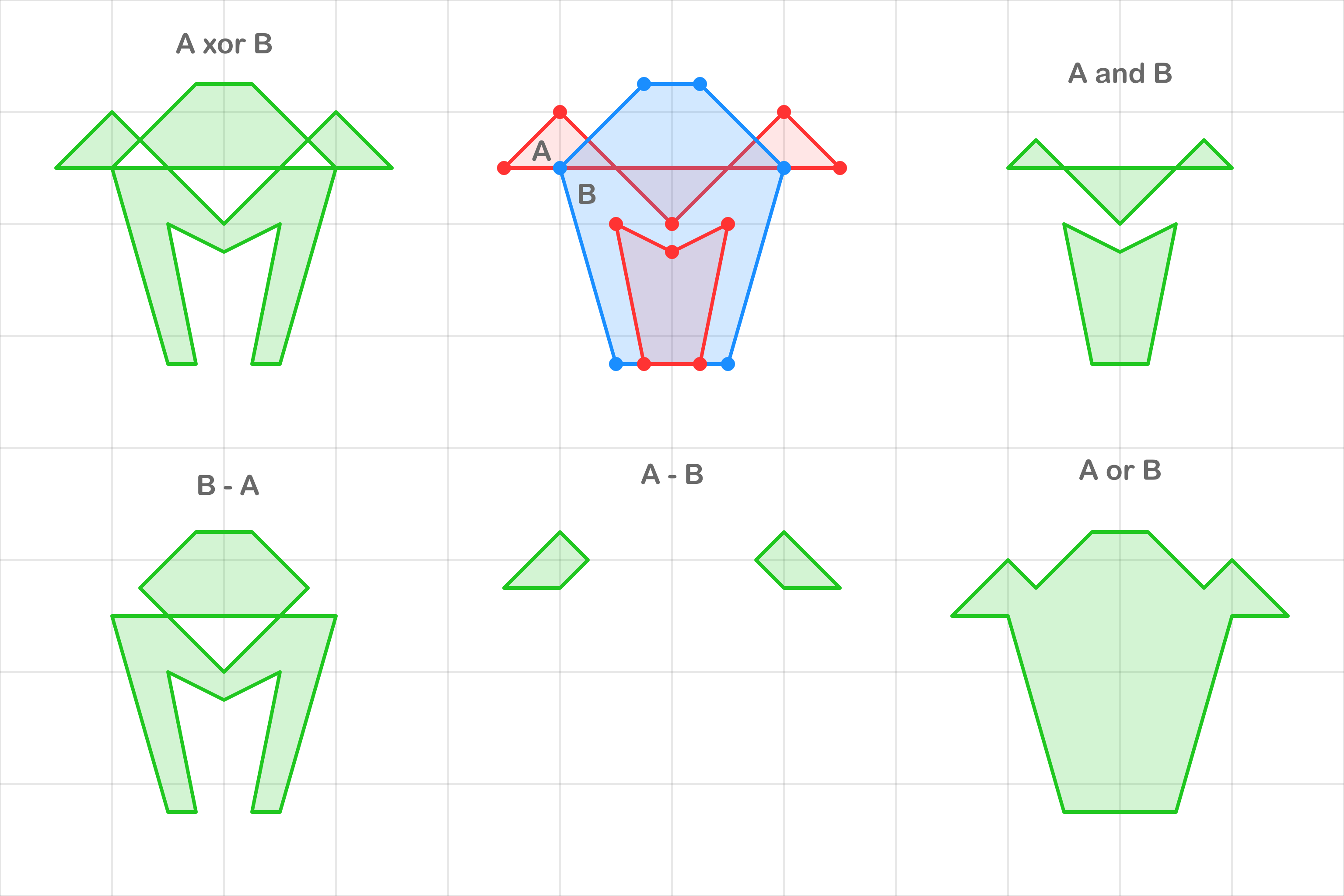
Итак, представьте, что у нас есть 2 тела: A (красное) и B (синее). Такое тело мы задаем группой контуров. Контур — это список последовательно соединенных вершин, всегда замкнутый и допускающий самопересечения.

Наша цель — получить новое тело C(зеленое), которое является одной из следующих комбинаций:

• Объединение C = A or B

• Пересечение C = A and B

• Исключение C = A xor B

• Разница C = A - B или B - A

Граф наложений

Давайте проделаем следующую манипуляцию с A и B.

• Разобьем все сегменты так, чтобы не осталось самопересечений.

• Для каждого сегмента добавим информацию о том, принадлежит ли он телу A или B, и если принадлежит, то с какой стороны.

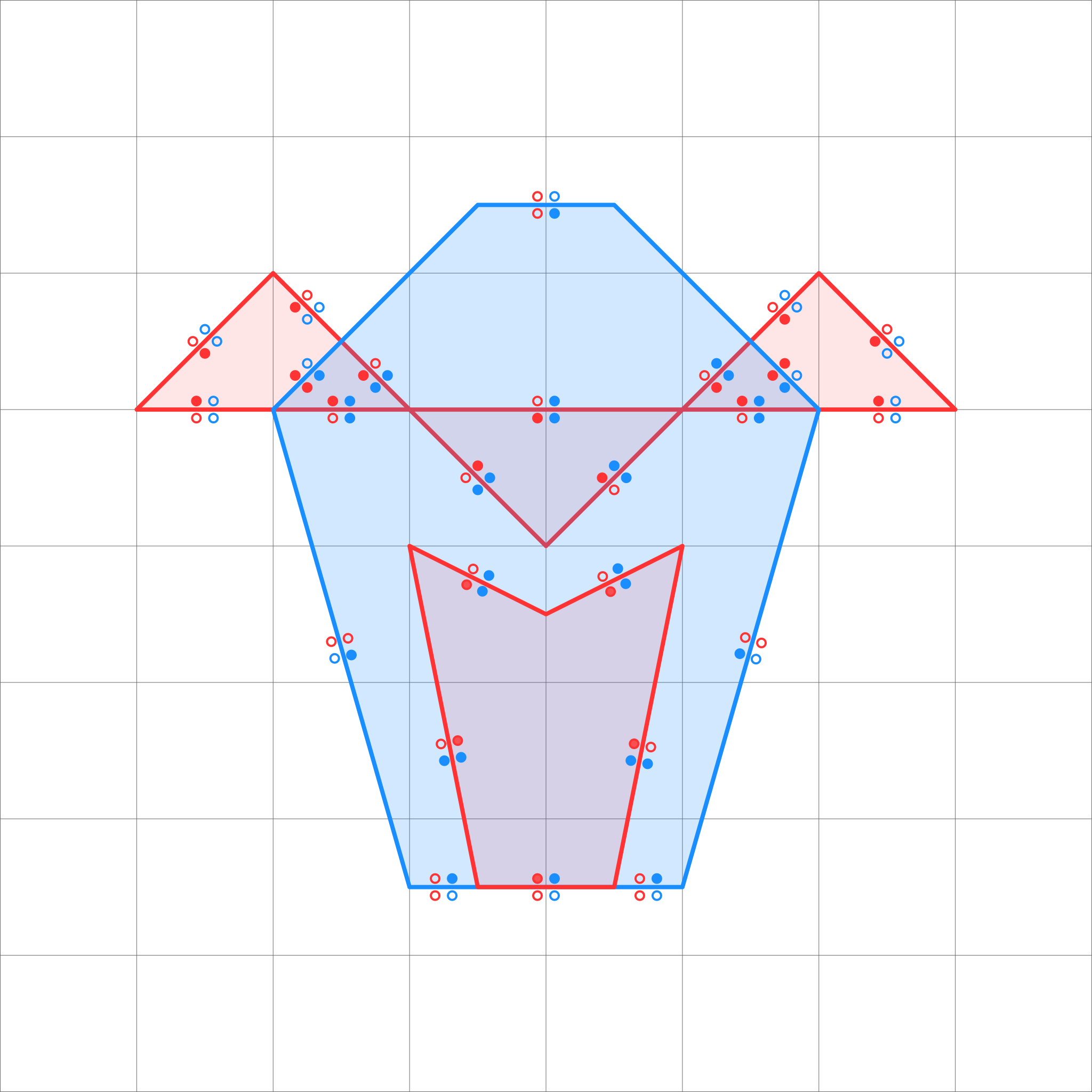
Такая структура называется графом наложений и позволяет извлекать контуры на основе булевых фильтров. Те, кто желает понять его лучше, могут покрутить этот пример в онлайн-редакторе здесь.

Теперь давайте рассмотрим, как извлекать контуры на простом примере.

Разность A - B

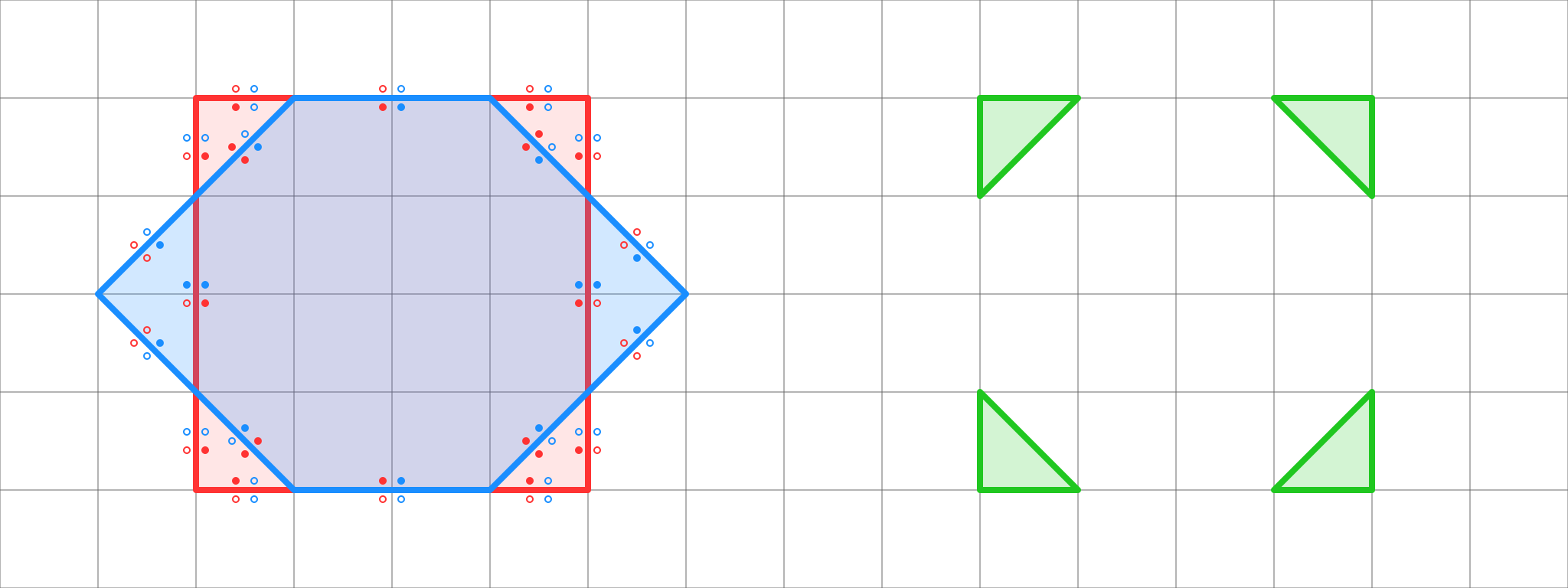
Как видно из рисунка, сегменты C не могут находиться внутри тела B и должны с одного края принадлежать телу A. Более того мы всегда можем определить где у сегментов C внутреняя часть, а где внешняя.

Объединение A or B

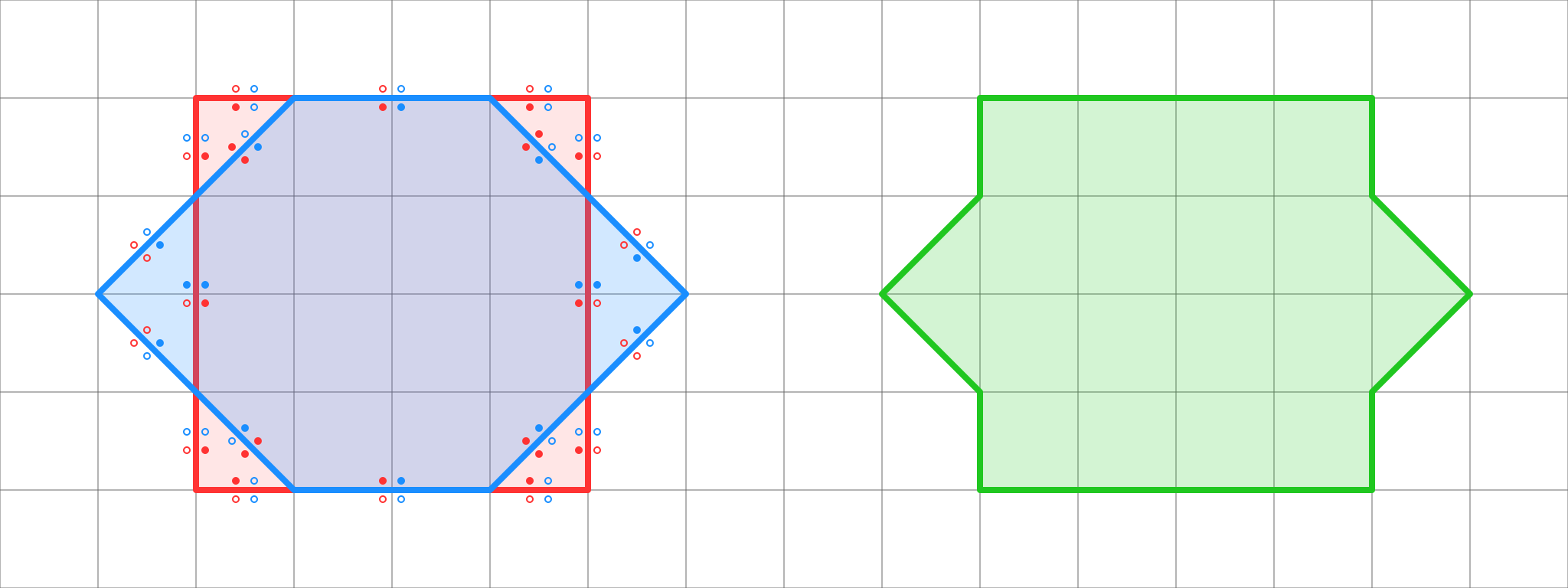
Здесь сегменты C не могут находиться внутри тела A или B и должны с одного края принадлежать либо A либо B либо сразу и A и B.

Пересечение A and B

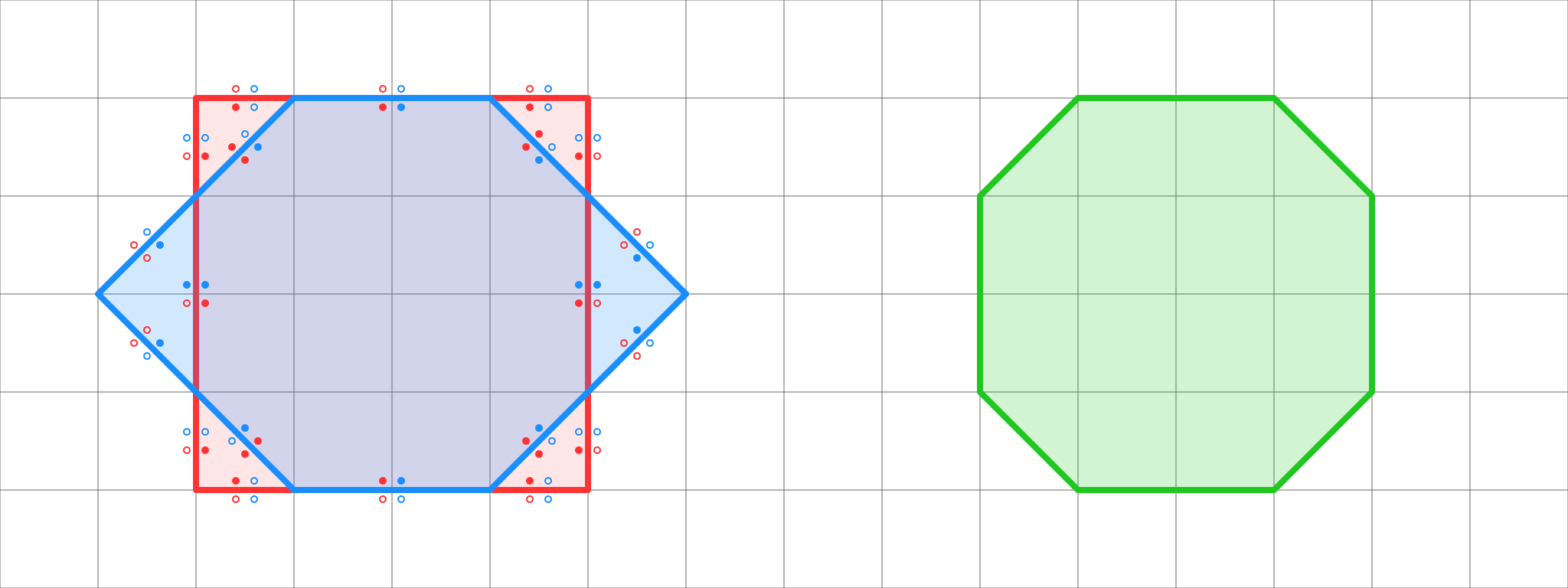
Сегмент C не могут одновременно находиться внутри обоих тел, но должны с одного края принадлежать и A, и B.

Построение контура

После фильтрации сегментов следующим шагом является построение контуров тела C. Рассмотрим это на примере разности A - B.

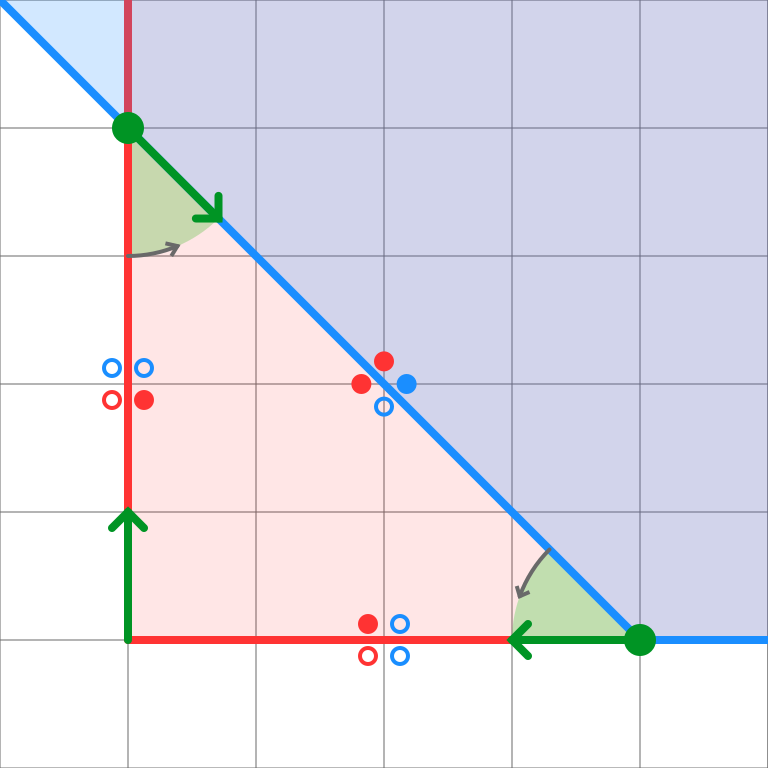
Обход графа будем осуществлять только по сегментам/ребрам тела С

Начнем обход с самой левой вершины и выберем самое верхнее ребро. Далее будем переходить от ребра к вершине и к следующему ребру так, чтобы внутренняя часть тела С всегда оставалась с одной стороны от хода движения. Рано или поздно мы вернемся к началу, завершив построение первого контура.

После этого переходим к поиску следующего контура. Алгоритм тот же: начинаем с самой левой вершины. Процесс продолжается, пока остаются непосещенные ребра.

В результате мы можем получить несколько замкнутых контуров. Часть из них описывает внешний периметр, а часть — внутренний (дырки).

По первому сегменту, с которого начинался контур, всегда можно определить тип периметра: внешний или внутренний. Если полость находится сверху — это внешний периметр, иначе — внутренний (дырка).

Сопоставляем дыры

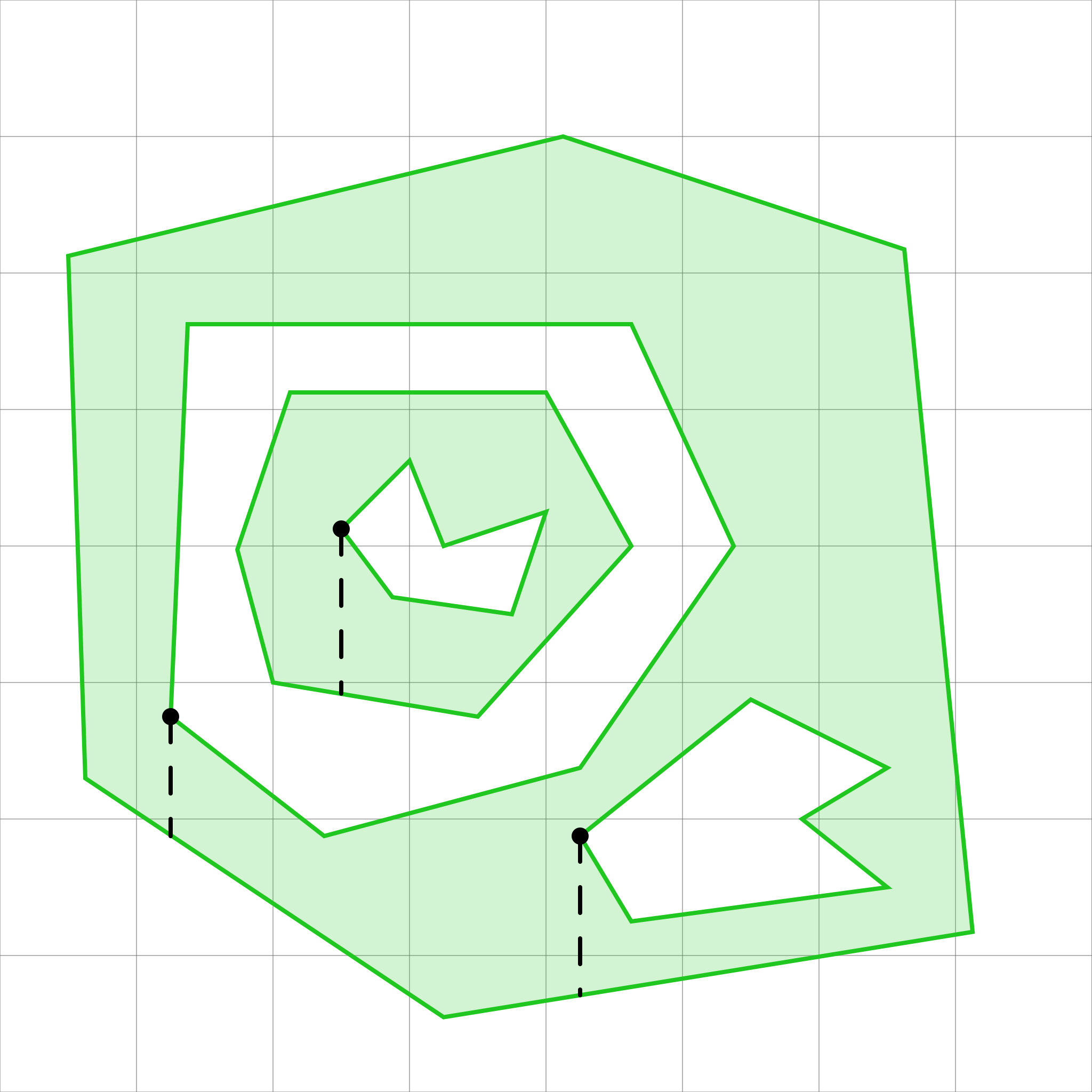
Теперь нужно сопоставить каждую дырку с ее внешним контуром. Для этого можно использовать самый левый угол дырки и найти ближайший сегмент под ним. Контур этого сегмента будет внешним для данной дырки.

Определение сегмента под точкой

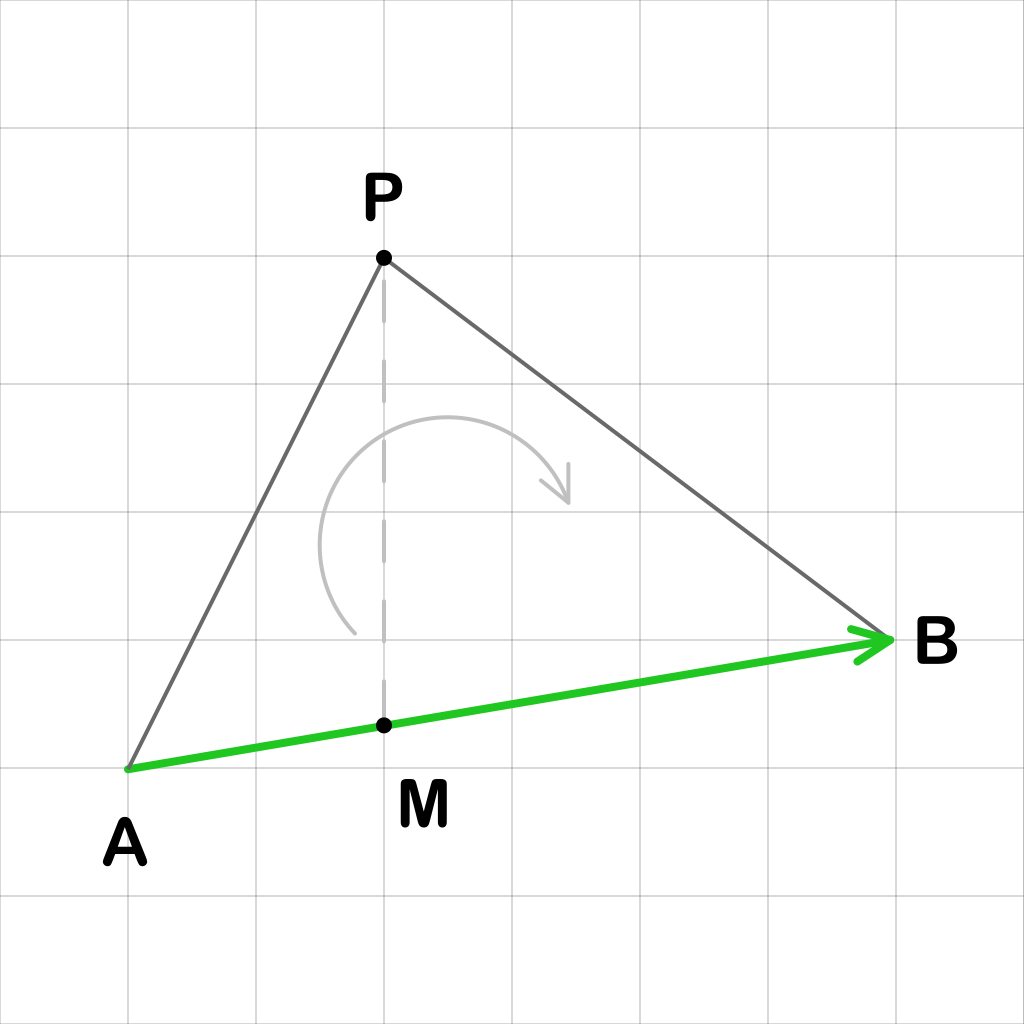
Изначально может показаться, что для определения того, находится ли отрезок AB под точкой P, достаточно сбросить перпендикуляр из P на AB и по положению точки пересечения M судить об этом. Однако, из-за операции деления этот метод может давать погрешности. Поэтому более надежным методом является использование порядка обхода вершин треугольника APB. Если отрезок AB находится под точкой P, то вершины A, P и B будут идти против часовой стрелки.

Этот метод связан с векторным произведением векторов PA и PB, которое вычисляется по формуле:

Поскольку здесь нет операции деления, метод не подвержен проблемам точности, что делает его абсолютно стабильным.

Мы определили, что отрезок находится под точкой, но как понять является ли он ближайшим? Для этого нам потребуется еще один метод, который определяет является ли один отрезок выше другого.

Сравнение отрезков по высоте

Этот случай распадается на 3:

Совпадает левый конец

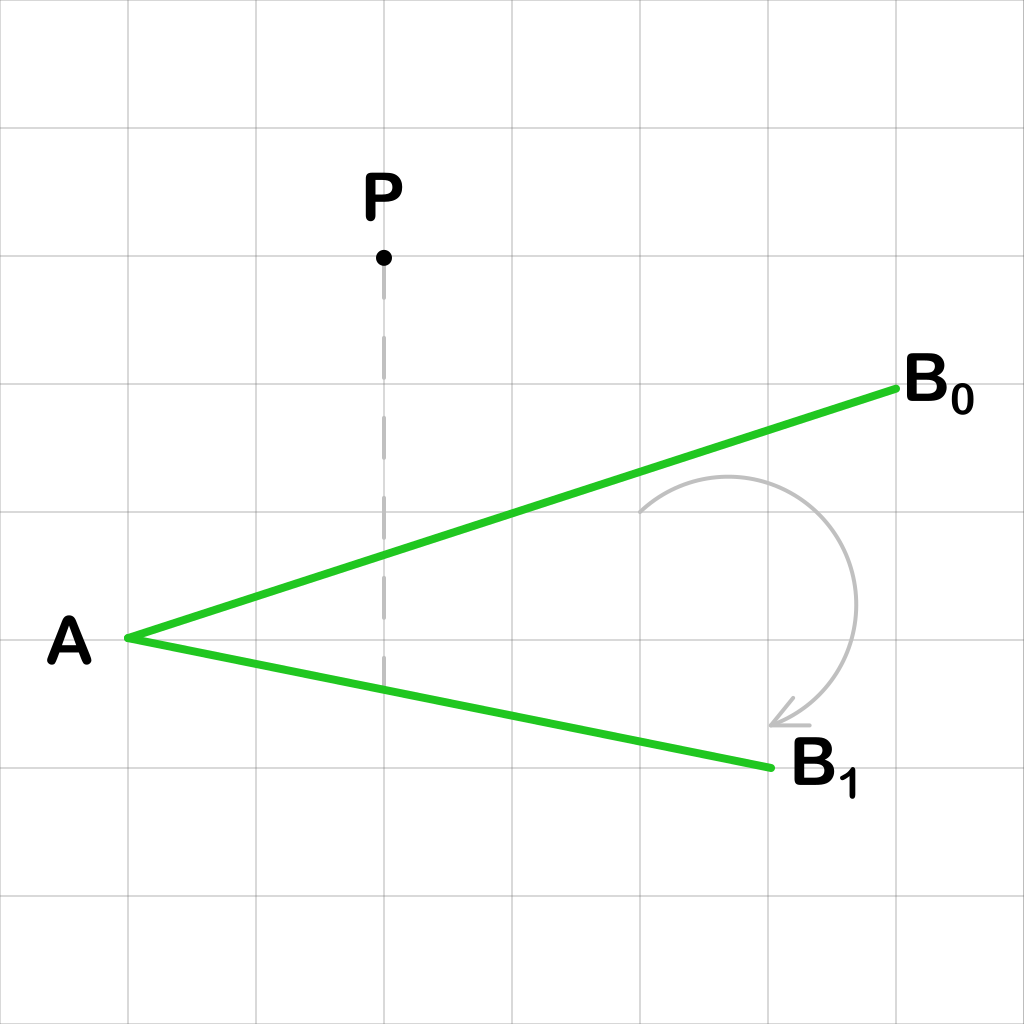
В этом случае, оба отрезка AB₀ и AB₁ имеют общую левую вершину, и мы проверяем, какой из них расположен ниже по отношению к точке P. Для этого мы строим треугольник с вершинами A, B₀ и B₁. Если вершины идут против часовой стрелки, отрезок AB₁ ниже AB₀.

Совпадает правый конец

Когда оба отрезка имеют общую правую вершину B, аналогично, проверяем расположение их левых концов. Если вершины A₀, A₁ и B следуют против часовой стрелки, отрезок A₀B ниже A₁B.

Общий случай

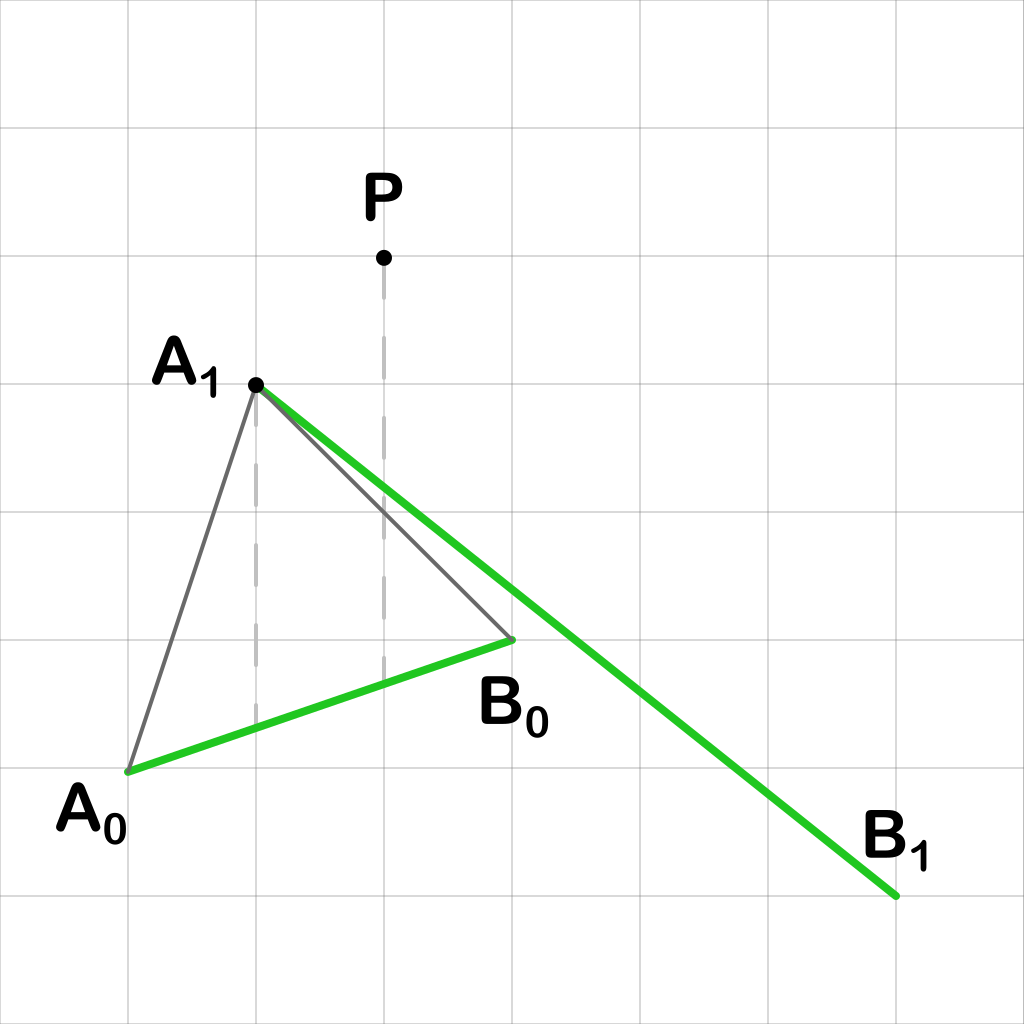
Здесь можно использовать метод сравнения одной из вершин (например, A₁ или B₀), которая находится внутри противоположного отрезка. Применив правило сравнения точки и отрезка, мы можем точно определить, какой отрезок находится выше.

Финальное решение

Обычно решения группируются по внешним контурам. Один внешний контур можетсодержать несколько дыр, и важно правильно их сопоставить. Часто направление следования вершин во внешнем и внутреннем контурах противоположное: внешний контур перечисляется по часовой стрелке, а внутренний — против. Это противоположное направление бывает полезным в алгоритмах обработки полигонов, таких как триангуляция или поиск узких мест, так как упрощает процесс, позволяя не задумываться о том, принадлежит ли сегмент внешнему или внутреннему контуру.

Что осталось за кадром

• Правило заполнения EvenOdd/NonZero: В зависимости от выбранного правила заполнения, результат операции может существенно отличаться. Это важный нюанс, который нужно учитывать в сложной геометрии.

• Построение графа наложений: Я лишь кратко упомянули о графе наложений, но не рассмотрел, как именно его строить. Этот процесс заслуживает отдельной статьи.

• Гарантия сходимости графа: Для получения правильного результата граф наложений должен всегда сходиться, но это требует особого подхода к обработке данных и вычислений, чтобы избежать ошибок и неточностей.

• Проблема погрешности и точности: Геометрические вычисления часто сталкиваются с проблемой погрешности, особенно при работе с числами с плавающей запятой. Одним из решений этой проблемы является использование целочисленных (int) вычислений вместо вычислений с плавающей запятой (float).

• Реализация: Я раскрыл только идею алгоритма, но абсолютно не затронул, как он реализуется. Какие у него слабые, а какие сильные стороны.

На правах рекламы

Если эта тема показалась вам интересной буду рад предложить вам свою реализацию доступную на нескольких языках:

• Swift Version: iShape-Swift/iOverlay

• Rust Version: iShape-Rust/iOverlay

• JS Version: iShape-Rust/iShape-js