На пути к Skein: просто и понятно про Blowfish

«От желудка иглобрюхих рыб отходят мешковидные выросты. При появлении опасности они наполняются водой или воздухом, из-за чего рыба становится похожой на раздувшийся шар
с торчащими шипиками. Шарообразное состояние делает рыб практически неуязвимыми. Если всё же достаточно крупный хищник попытается проглотить такой шар, то он застревает
в глотке у хищника, который впоследствии умирает»

К концу 1993 года в мире криптографии возникла очень неловкая ситуация. Алгоритм симметричного шифрования DES, со своим слабеньким 56-битным ключом, был близок к фиаско, а существующие на тот момент альтернативные варианты, такие как Khufu, REDOC II, IDEA были защищены патентами и не доступны для свободного использования. Алгоритмы RC2 и RC4, разработанные в то время компанией RSA Security, также требовали проведение процедуры лицензирования. И в целом, индустрия криптографии в рамках государственных организаций и крупных корпораций была обращена в сторону использования секретных алгоритмов, таких как Skipjack.

Возник определенный ваккум. Необходим был алгоритм шифрования, более криптостойкий нежели отмирающий DES, и в то же время без каких-либо ограничений на право своего использования.

И он появился.

В 1994 году, на семинаре Fast Software Encryption в Кембридже, а впоследствии и в журнале «Lecture Notes in Computer Science» (#809, 1994), Брюс Шнайер презентовал свой алгоритм блочного шифра, который был назван Blowfish.

Отличительными особенностями этого алгоритма стала более высокая степень криптостойкости, нежели алгоритма DES (в том числе за счет использования переменной длины ключа, до 448 бит), высокая скорость шифрации/дешифрации (за счет генерации таблиц замены) и конечно — возможность его свободного применение для любых целей.

Оригинальная статья Брюса Шнайера от 1994 года из архива:
Block Ciphers II, Bruce Schneier (внизу страницы):
Description of a New Variable-Length Key, 64-bit Block Cipher (Blowfish). 191-204

Или в формате PDF

Введение

BlowFish — алгоритм 64-битного блочного шифра с ключом переменной длины. Был разработан известным специалистом в области криптографии и защиты информации Брюсом Шнайером (Bruce Schneier) в 1993 году.

В общем случае алгоритм состоит из двух этапов — расширение ключа и шифрация/дешифрация исходных данных.

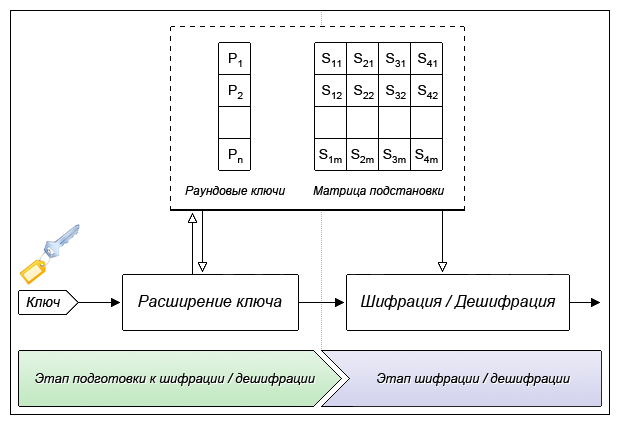
На этапе расширения ключа, исходный ключ преобразуется в матрицу раундовых ключей (P)
и матрицу подстановки (S, Substitution-box) (или замены), общим объемом в 4168 байт. По всей вероятности, этим «расширением» (от 448 бит до 4168 байт) и объясняется выбор названия
алгоритма Blowfish.

Шифрация данных, а также создания матрицы раундовых ключей и подстановки, происходит через использование сети Фейстеля, состоящей в свою очередь из 16 раундов. Поэтому, перед тем, как рассмотреть этапы расширения ключа и шифрации данных в деталях, нам необходимо определиться, что из себя представляет упомянутая сеть Фейстеля.

В процессе, мы реализуем программный код шифратора по алгоритму Blowfish на языке C++. Готовые реализации для языков высокого уровня (такие как C/C++/Haskell/Perl/…) доступны на странице
с исходными кодами на сайте Брюса Шнайера.

Сеть Фейстеля

В 1971 году, «крестный отец» стандарта DES, Хорст Фейстель (Horst Feistel), в стенах корпорации IBM, разработал два устройства, реализовавшие различные алгоритмы шифрования, названные затем общим название «Люцифер». В одной из этих устройств он использовал схему, которую впоследствии назвали Сетью Фейстеля. Эта сеть представляет собой определённую многократно итерированную (повторяющуюся) структуру, которою называют ячейкой Фейстеля.

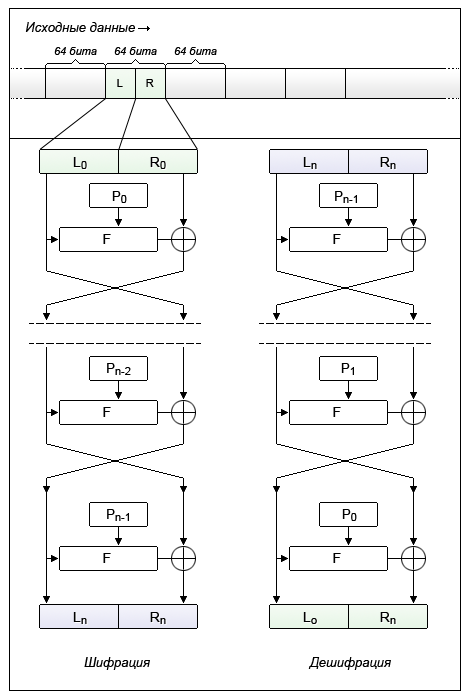
Принцип работы сети достаточно прост:

1. Исходные данные разбиваются на блоки фиксированной длины (как правило кратно степени двойки — 64 бит, 128 бит). В случае если длина блока исходных данных меньше длины разрядности шифра, то блок дополняется каким-либо заранее известным образом.
2. Блок делится на два равных подблока — «левый» L₀ и «правый» R₀.
   В случае 64-битной разрядности — на два блока с длиной 32 бита каждый.

3. «Левый подблок» L₀ видоизменяется функцией итерации F(L₀, P₀) в зависимости от ключа P₀,
   после чего он складывается по модулю 2 (XOR) с «правым подблоком» R₀.

4. Результат сложения присваивается новому левому подблоку L₁, который становится левой половиной входных данных для следующего раунда, а «левый подблок» L₀ присваивается без изменений новому правому подблоку R₁, который становится правой половиной.
5. Эта операция повторяется n-1 раз, при этом при переходе от одного этапа к другому меняются раундовые ключи (P₀, P₁, P₂ и т.д.), где n — количество раундов для используемого алгоритма.

Процесс расшифрования аналогичен процессу шифрования за исключением того, что раундовые ключи используются в обратном порядке.

Вернемся к алгоритму Blowfish.

В общем случае, алгоритм шифрования Blowfish представляет собой сеть Фейстеля, но с некоторыми особенностями генерации и использования раундовых ключей (P₀, P₁ …).

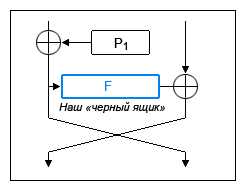
Для начала допустим, что функция итерации F в алгоритме Blowfish это некоторый «черный ящик», который принимает на входе и выдает на выходе 32-битное число (DWORD).

При этом 32-битные раундовые ключи Pn:

1. вычисляются по некоторому правилу от исходного ключа (длиной до 448 бит);
2. не являются аргументами для функции итерации F;
3. непосредственно складываются по модулю 2 (XOR) с «левым блоком».
   Результат этой операции является входящим 32-битным аргументом для функции F.

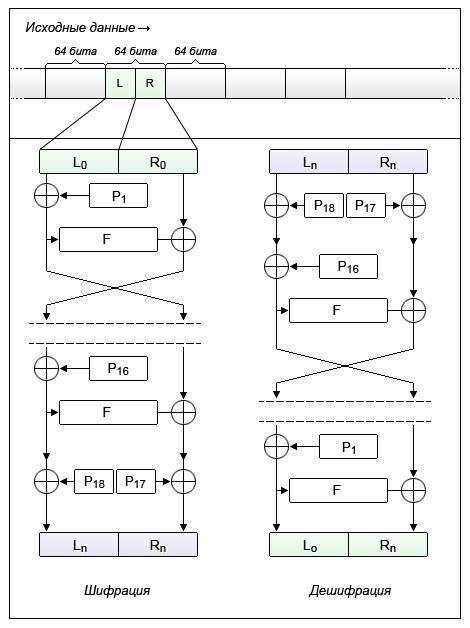
В алгоритме Blowfish при шифрации выполняется 16 раундов (внутри сети Фейстеля), а 17-й и 18-й ключи складываются с левым и правым выходным блоком последнего раунда. Такое количество раундов было выбрано, поскольку именно оно определяет длину возможного ключа.

Но здесь у внимательного читателя может возникнуть вопрос: если используется 18 раундовых ключей, каждый из которых имеет длину 32 бита, то в итоге мы получаем ключ длиной 576 бит (18 ключей × 32 бита). Почему же длина исходного ключа в Blowfish изначально ограничена 448 битами?

Ответ прост — она не ограничена. Можно использовать ключи до 576 бит. Но! Ограничение было сделано исходя из требований к соблюдению безопасности и криптостойкости алгоритма.

Давайте реализуем сеть Фейстеля для алгоритма Blowfish на языке C++:

void swap(unsigned long *a, unsigned long *b)
{
    unsigned long temp;
    if (a && b) {
        temp = *a, *a = *b, *b = temp;
    }
}

void blowfish_encrypt_block(blowfish_ctx *ctx, unsigned long *high, unsigned long *low)
{
    int i;
    for (i = 0; i < 16; i++) {
        *high ^= ctx->p[i];
        *low ^= F(ctx, *high);
        swap(low, high);
    }
    swap(low, high);
    *low ^= ctx->p[16];
    *high ^= ctx->p[17];
}

Расширение ключа (Blow it up!)

Подготовительным этапом алгоритма Blowfish является этап расширения ключей. В процессе этого этапа строится матрица раундовых ключей Pn и матрица подстановки — 4 блока замены S-Box (Substitution-box), каждый из которых состоит из 256 32-х битных элементов.

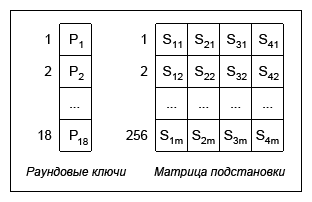
Элементы этих матриц шифруются (вычисляются) с помощью рассмотренной выше сети Фейстеля для алгоритма Blowfish. Таким образом, сеть Фейстеля в алгоритме Blowfish используется:

• для шифрации/дешифрации исходных данных;
• для генерации матрицы раундовых ключей и матрицы подстановки (т.е. расширения ключа).

Сгенерированная матрица раундовых ключей и матрицы подстановки впоследствии используются
в процессе шифрации/дешифрации.

В процессе расширения ключа обрабатывается
18 × 32 (P₁,P₂ …) + 4 × 256 × 32 (S₁—S₄) = 33344 бит или 4168 байт данных.

При этом выполняется (18 (Pn) + 4 × 256 (S₁—S₄)) / 2 = 521 полная итерация сети Фейстеля.

Всё это является весьма трудозатратной операцией, и именно поэтому алгоритм Blowfish
не рекомендуется использовать там, где требуется частая смена ключа.

Опишем алгоритм расширения ключа.

1. Выбирается «искреннее число» (или иначе — «Nothing up my sleeve number»). Это такое число, которое изначально не содержит каких-либо повторяющихся последовательностей и является известным. Делается это для того, чтобы показать, что константа разработчиками была выбрана без преследования каких-то «гнусных» целей, наприимер для создания лазейки в алгоритме (backdoor).

   В качестве такого искреннего числа в Blowfish обычно используется число PI. Вычислять шестнадцатеричное представление значение числа PI мы не будем, а воспользуемся уже готовым решением: 8366 шестнадцатеричных цифр мантиссы для числа PI.

2. Значением мантиссы числа PI заполняется матрица раундовых ключей (FIXED_P) и матрицы подстановки (FIXED_S):

   typedef struct _blowfish_ctx
   {
       unsigned long p[18];
       unsigned long sbox[4][256];
   } blowfish_ctx;
   
   const unsigned int FIXED_S[4][256] = {
       {
           0xD1310BA6, 0x98DFB5AC, 0x2FFD72DB, 0xD01ADFB7,
           0xB8E1AFED, 0x6A267E96, 0xBA7C9045, 0xF12C7F99,
           0x24A19947, 0xB3916CF7, 0x0801F2E2, 0x858EFC16,
           0x636920D8, 0x71574E69, 0xA458FEA3, 0xF4933D7E,
           0x0D95748F, 0x728EB658, 0x718BCD58, 0x82154AEE,
           0x7B54A41D, 0xC25A59B5, 0x9C30D539, 0x2AF26013,
           .... Часть значений не указаны ради экономии места ....
           0xB74E6132, 0xCE77E25B, 0x578FDFE3, 0x3AC372E6
       }
   };
   
   const unsigned long FIXED_P[] = {
       0x243F6A88, 0x85A308D3, 0x13198A2E, 0x03707344,
       0xA4093822, 0x299F31D0, 0x082EFA98, 0xEC4E6C89,
       0x452821E6, 0x38D01377, 0xBE5466CF, 0x34E90C6C,
       0xC0AC29B7, 0xC97C50DD, 0x3F84D5B5, 0xB5470917,
       0x9216D5D9, 0x8979FB1B
   };

3. Значение каждого раундового ключа Pn (P₁, P₂ …) складывается по модулю 2 (XOR) с соответст- вующим элементами исходного ключа K. Например, выполняется XOR раундового ключа P₁
   с первыми 32 битами исходного ключа K, P₂ со вторыми 32 битами исходного ключа K и так далее. Если исходный ключ K короче длины всех раундовых ключей (576 бит), то он конкатенируется сам
   с собой: KK, KKK и так далее.

   for(i = 0, k = 0; i < 18; i++) {
       for(j = 0, long_key = 0; j < 4; j++, k++) {
           long_key = (long_key << 8) | key[k % key_len];
       }
       ctx->p[i] ^= long_key;
   }

4. Далее нам необходимо зашифровать (вычислить новые значения) элементов матрицы раундовых ключей и матрицы подстановки. Для этого мы воспользуемся реализованным нами алгоритмом сети Фейстеля для Blowfish.
   1. Используя текущие раундовые ключи P₁—P₁₈ и матрицы подстановок S₁—S₄ (о том, где именно используются матрицы подстановок будет рассказано ниже), шифруем 64-битную последовательность нуля: 0x00000000 0x00000000, а результат записываем в P₁ и P₂.
   2. P₁ и P₂ шифруются изменёнными значениями раундовых ключей и матриц подстановки, результат записывается соответственно в P₃ и P₄.
   3. Шифрование продолжается до изменения всех раундовых ключей P₁—P₁₈ и элементов матриц подстановок S₁—S₄.

      Т.е. в конечном счете нам надо получить результат вычисления по схеме cети Фейстеля алгоритма Blowfish для (18 Pn + 4 × 256 (S₁—S₄)) / 2 = 521 итераций. Мы поделили на 2, поскольку за кажду итерацию мы вычисляем сразу два новых значения для элементов матрицы раундовых ключей или матрицы подстановок.

   for (i = 0, k = 0, l = 0; i < 18; i++) {
       blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l);
       ctx->p[i] = k;
       ctx->p[++i] = l;
   }
   for (i = 0; i < 4; i++) {
       for (j = 0; j < 256; j++) {
           blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l);
           ctx->sbox[i][j] = k;
           ctx->sbox[i][++j] = l;
       }
   }

На этом, подготовительный этап алгоритма Blowfish — расширение ключа — завершается. Но перед тем, как рассмотреть этап шифрации/дешифрации, давайте все-таки раскроем наш «черный ящик» — функцию F, исполняемую на каждом раунде внутри итераций сети Фейстеля для алгоритма Blowfish.

Функция итерации (раунда)

Функция раунда или итерации (поскольку она общая для всей используемой сети Фейстеля) весьма проста и использует лишь несколько логических операций над матрицей подстановок. Изначально, разрабатывая «Люцифера», Хорст Фейстель даже предполагал использование для матрицы подстановок электронного блока с простой линейной схемой.

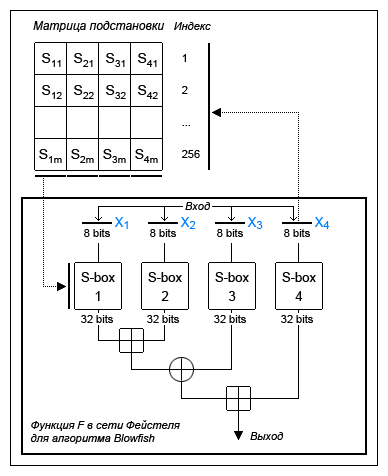
Итак:

1. Входящий 32-битный блок делится на четыре 8-битных блока, назовем их X₁, X₂, X₃, X₄
   (см. рисунок выше).

2. Каждый каждый из которых является индексом массива таблицы замен S₁—S₄.
3. значения S₁[X₁] и S₂[X₂] складываются по модулю 2³², затем результат складывается
   по модулю 2 (XOR) с S₃[X₃] и, наконец, складываются с S₄[X₄] опять же по модулю 2³².
4. Результат вычислений и будет значением функции F(X₁—X₄).

Формула функции:

Всё крайне просто. Функция использует матрицы подстановок S₁—S₄ для того, чтобы линейно преобразовать входящие 32 бита данных в значение из матрицы подстановки. А сами значения
в матрицах подстановки вычисляются на рассмотренном нами ранее этапе расширения ключа.

Реализация функции на языке C++:

unsigned long F(blowfish_ctx *ctx, unsigned long x)
{
    return ((ctx->sbox[0][(x >> 24) & 0xFF] + ctx->sbox[1][(x >> 16) & 0xFF]) ^
      ctx->sbox[2][(x >> 8) & 0xFF]) + ctx->sbox[3][(x) & 0xFF];
}

А теперь давайте перейдем собственно к процессу шифрации исходных данных.

Шифрация / дешифрация исходных данных

Сюрприз! На самом деле алгоритм шифрации и дешифрации исходных данных мы уже рассмотрели. Все дело в том, что как мы заметили в самом начале, шифрация / дешифрация данных, и создание вышеупомянутой матрицы раундовых ключей и матрицы подстановки, происходит с помощью рассмотренной сети Фейстеля для алгоритма Blowfish.

Т.е. в нашей программной реализации, весь процесс шифрации исходных данных строится по аналогии с процессом шифрации на этапе расширения ключа. Т.е. представляет собой итеративное исполнение функции blowfish_encrypt_block (реализация сети Фейстеля) над каждыми 64 битами исходных данных. Раундовые ключи P (P₁, P₂, &hellip) и матрицы подстановки S₁—S₄ являются входными параметрами соответственно для сети Фейстеля и функции F внутри этой сети.

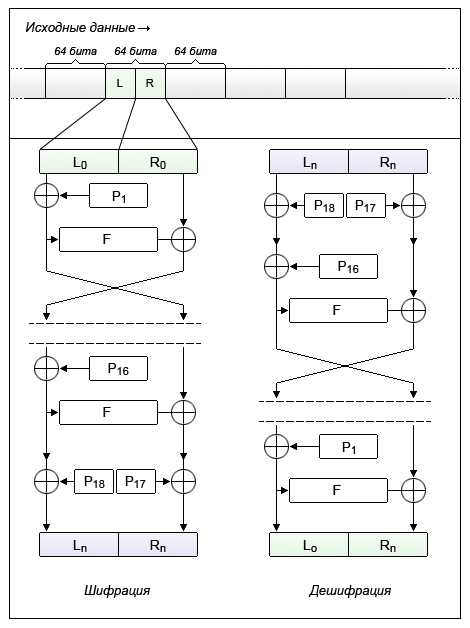
В итоге, если резюмировать алгоритм шифрации или дешифрации в алгоритме Blowfish,
то получим следующие шаги:

1. Выделяем массив из 18 элементов для раундовых ключей сети Фейстеля и 4 матриц подстановки по 256 элементов в каждой.
2. Заполняем выделенный массив значением мантиссы числа PI.
3. Делаем итеративный XOR: Pi = Pi XOR Ki (где Pi — раундовый ключ, а Ki — исходный ключ).
4. Шифруем раундовые ключи и матрицы подстановки с помощью сети Фейстеля (в качестве входящего параметра для функции внутри сети используются матрица подстановки; раундовые ключи внутри сети берутся из матрицы раундовых ключей).
5. Шифруем/дешифруем блоки исходных данных по 64 бита также с помощью сети Фейстеля.

Всё просто.

Резюме

Дорогие читатели. Уметь описать сложные вещи простыми словами — очень сложно.

Перед тем, как начать писать данный текст, я попытался поставить себя на место разработчика,
который хочет попытаться изучить рассмотренный алгоритм Blowfish.

Так, я поставил целью найти в сети документ, описывающий данный алгоритм с достаточной, для его понимания, полнотой. В итоге, я конечно попадал и на страницы Википедии, и на форумы, и даже на разные курсовые работы. Но читая представленное там описание зачастую возникало больше вопросов нежели ответов.

Всё это утвердило меня в мысли, что простое и в то же время подробное описание с примерами будет полезным и востребованным. Поэтому, со своей стороны я постарался по мере возможности «расставить все по полкам». А вот насколько хорошо у меня это получилось — судить вам.

Спасибо.
Yours sincerely, A.B.

p.s. Планируется продолжение…

Автор: security