Новый прорыв приближает умножение матриц к идеалу

Устранив скрытую неэффективность, учёные придумали новый способ умножения больших матриц, который работает быстрее, чем когда-либо.

Учёные, занимающиеся информатикой, — это требовательная группа. Им недостаточно получить правильный ответ — цель почти всегда состоит в том, чтобы получить ответ как можно эффективнее.

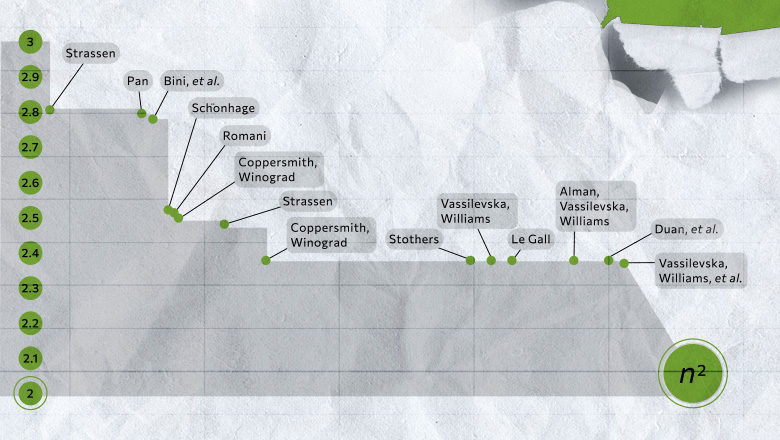
Возьмем, к примеру, умножение матриц или массивов чисел. В 1812 году французский математик Жак Филипп Мари Бине разработал базовый набор правил, которым мы до сих пор обучаем студентов. Это работает прекрасно, но другие математики нашли способы упростить и ускорить процесс умножения матриц. Эта задача лежит на стыке математики и информатики, и исследователи продолжают совершенствовать процесс её решения — хотя в последние десятилетия достижения были довольно скромными. С 1987 года численные улучшения в умножении матриц были «небольшими и… чрезвычайно трудными для достижения», — сказал Франсуа Ле Галль, учёный из Нагойского университета.

Теперь трое исследователей — Ран Дуань и Рэньфэй Чжоу из Университета Цинхуа и Хунсюнь Ву из Калифорнийского университета в Бёркли — сделали большой шаг вперед в решении этой извечной проблемы. По словам Ле Галля, их новые результаты, представленные в ноябре прошлого года на конференции «Основы компьютерных наук», базируются на неожиданной новой методике. Хотя само по себе улучшение было относительно небольшим, Ле Галль назвал его «концептуально бо́льшим, чем предыдущие».

Этот метод открывает ранее неизвестный и, следовательно, неиспользованный источник потенциальных улучшений, и он уже принес свои плоды: вторая статья, опубликованная в январе, основывается на первой и показывает, как можно ещё больше ускорить умножение матриц.

«Это крупный технический прорыв, — сказал Уильям Кушмаул, учёный в области теоретической информатики из Гарвардского университета. — Это самое большое улучшение в матричном умножении, которое мы видели более чем за десятилетие».

Вход в Матрицу

Это может показаться незначительной проблемой, но умножение матриц — фундаментальная вычислительная операция. Она включена в большую часть алгоритмов, которые люди используют каждый день для самых разных задач: от отображения более четкой компьютерной графики до решения логистических задач в теории сетей. И, как и в других областях вычислений, скорость имеет первостепенное значение. Даже небольшие улучшения могут в конечном итоге привести к значительной экономии времени, вычислительной мощности и денег. Но на данный момент теоретики в основном заинтересованы в том, чтобы выяснить, насколько быстрым в принципе может быть этот процесс. 

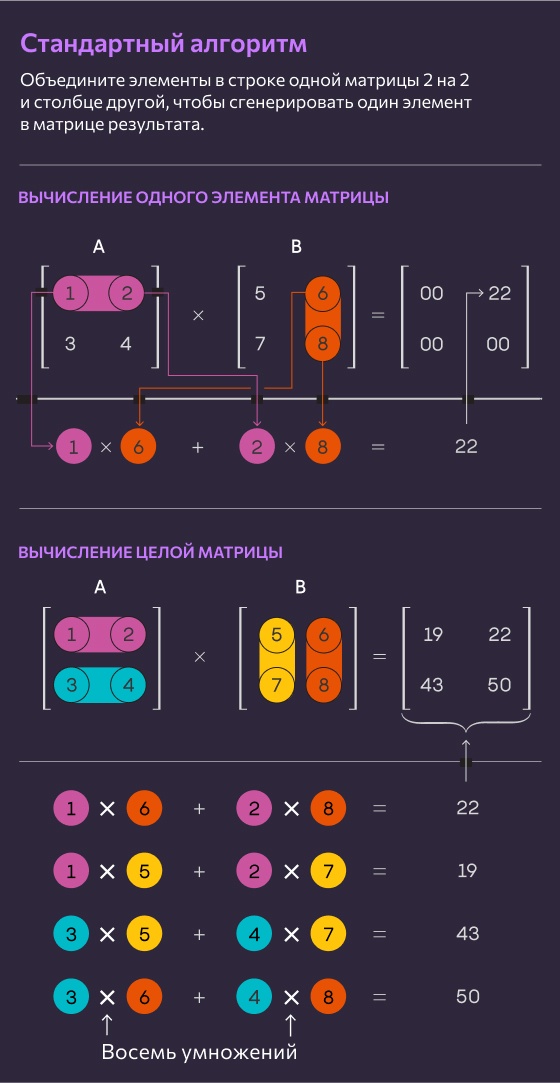
Традиционный способ умножения двух матриц размером n на n — путем умножения чисел из каждой строки первой матрицы на числа в столбцах второй — требует n³ отдельных умножений. Для матриц 2 на 2 это означает 2³ или 8 умножений.

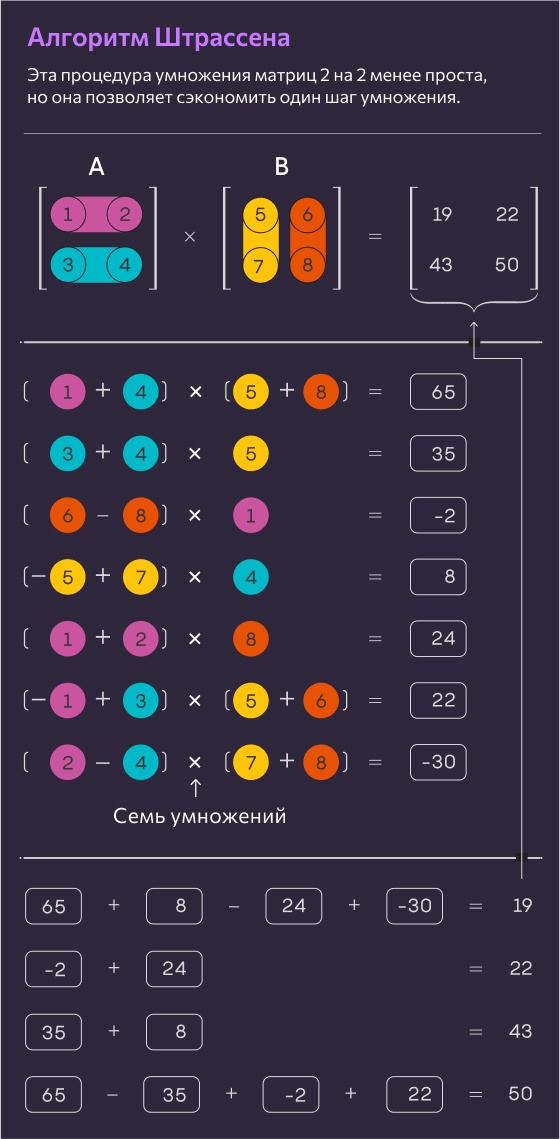
В 1969 году математик Фолькер Штрассен открыл более сложную процедуру, позволяющую умножать матрицы 2 на 2 всего за семь умножений и 18 сложений. Два года спустя учёный Шмуэль Виноград продемонстрировал, что семь умножений действительно являются абсолютным минимумом для матриц 2 на 2.

Штрассен использовал ту же идею, чтобы показать, что все большие матрицы размером n на n также можно умножить менее чем за n³ шагов. Ключевым элементом этой стратегии является процедура, называемая декомпозицией. Так называют разбиение большой матрицы на последовательно меньшие подматрицы, которые в конечном итоге могут оказаться размером всего 2 на 2 или даже 1 на 1 (это просто отдельные числа).

По мнению Вирджинии Василевской Уильямс, специалиста по информатике из Массачусетского технологического института и соавтора второй статьи, причина разделения гигантского массива на крошечные части довольно проста. «Человеку трудно взглянуть на большую матрицу (скажем, порядка 100 на 100) и придумать наилучший возможный алгоритм», — сказала Василевска Уильямс. Даже матрицы 3 на 3 ещё не решены полностью. «Тем не менее можно использовать быстрый алгоритм, который уже разработан для маленьких матриц, чтобы получить быстрый алгоритм и для больших матриц».

Ключом к скорости, как определили исследователи, является сокращение количества шагов умножения, максимальное снижение показателя степени n³ (для стандартного метода). Наименьшее возможное значение, n², по сути, равно числу шагов, необходимому только для написания ответа. Учёные называют этот показатель омегой, ω, где n^ω — это наименьшее количество возможных шагов, необходимых для успешного умножения двух матриц размером n на n, когда n становится очень большим. «Цель этой работы, — сказал Чжоу, который также является соавтором статьи, опубликованной в январе 2024 года, — состоит в том, чтобы увидеть, насколько близко к 2 вы можете подойти, и можно ли этого достичь в теории».

Применяем лазерный метод

В 1986 году Штрассен совершил ещё один большой прорыв, когда представил так называемый лазерный метод умножения матриц. Штрассен использовал его, чтобы установить верхнее значение омеги в 2,48. Хотя этот метод является лишь одним из этапов умножения больших матриц, он является одним из наиболее важных, поскольку исследователи продолжают его совершенствовать.

Год спустя Виноград и Дон Копперсмит представили новый алгоритм, который прекрасно дополнил лазерный метод. Эта комбинация инструментов использовалась практически во всех последующих попытках ускорить умножение матриц.

Вот упрощённый способ мышления о том, как эти различные элементы сочетаются друг с другом. Начнём с двух больших матриц A и B, которые вы хотите перемножить. Сначала вы разлагаете их на множество более мелких подматриц или блоков, как их иногда называют. Далее вы можете использовать алгоритм Копперсмита и Винограда в качестве своего рода инструкции по обработке и, в конечном итоге, сборке блоков. «Он говорит мне, что умножать, что добавлять и какие записи куда направлять в итоговой матрице C, — сказала Василевска Уильямс. — Это просто рецепт создания C из A и B».

Однако есть одна загвоздка: иногда у вас возникают блоки, имеющие общие записи. Оставить их в результате было бы всё равно, что посчитать эти записи дважды, поэтому вам нужно избавиться от этих дублирующихся записей, называемых перекрытиями. Исследователи делают это, «убивая» блоки, в которых они находятся, — устанавливая их компоненты равными нулю, чтобы исключить их из расчета.

Вот здесь-то и вступает в действие лазерный метод Штрассена. «Лазерный метод обычно работает прекрасно и как правило находит хороший способ уничтожить подмножество блоков, чтобы устранить перекрытие», — сказал Ле Галль. После того, как лазер устранил или «сжёг» все перекрытия, вы можете построить конечную матрицу C.

Объединение этих методов приводит к алгоритму умножения двух матриц с небольшим количеством умножений в целом — по крайней мере, в теории. Лазерный метод не претендует на практичность; это просто способ подумать об идеальном процессе умножения матриц. «Мы никогда не запускаем этот метод на компьютере, — сказал Чжоу. — Мы его анализируем».

И именно этот анализ привёл к самому большому улучшению омеги за более чем десятилетие.

Обнаруженная потеря

В статье, опубликованной прошлым летом Дуанем, Чжоу и Ву, показано, что процесс Штрассена всё ещё можно значительно ускорить. Всё это произошло из-за концепции, которую они назвали скрытой потерей, заложенной глубоко в предыдущих анализах — «результате непреднамеренного уничтожения слишком большого количества блоков», — сказал Чжоу.

Лазерный метод заключается в маркировке перекрывающихся блоков как мусора, предназначенного для утилизации; остальные блоки считаются ценными и сохраняются. Однако процесс отбора несколько рандомизирован. Блок, оценённый как мусор, на самом деле может оказаться полезным. Это не было полной неожиданностью, но, изучив многие из этих случайных вариантов, команда Дуана определила, что лазерный метод систематически недооценивает блоки: нужно сохранять больше блоков и меньше выбрасывать. И, как это обычно бывает, меньше отходов приводит к большей эффективности.

«Возможность хранить больше блоков без перекрытия приводит к… более быстрому алгоритму умножения матриц», — сказал Ле Галль.

Доказав существование этой потери, команда Дуана изменила способ маркировки блоков лазерным методом, существенно сократив количество отходов. В результате они установили новую верхнюю границу омеги на отметке в 2,371866 — улучшение по сравнению с предыдущей верхней границей в 2,3728596, установленной в 2020 году Джошем Алманом и Василевской Уильямс. Это может показаться скромным изменением: граница снижается примерно на 0,001. Но это самое большое улучшение, которое учёные наблюдали с 2010 года. Для сравнения: результат Василевской Уильямс и Алмана за 2020 год улучшился по сравнению с его предшественником только на 0,00001.

Но больше всего исследователей волнует не новый рекорд, который просуществовал недолго. Важнее то , что эта статья открыла новый путь к улучшению, который до этого оставался совершенно незамеченным. По словам Ле Галля, на протяжении почти четырех десятилетий все полагались на один и тот же лазерный метод. «А потом они обнаружили, что мы можем добиться большего».

В статье, опубликованной в январе 2024 года, этот новый подход был усовершенствован, что позволило Василевской Уильямс, Чжоу и их соавторам ещё больше сократить скрытые потери. Это привело к дополнительному улучшению верхней границы омеги, снизив ее до 2,371552. Авторы также обобщили эту же технику для улучшения процесса умножения прямоугольных (n на m) матриц — процедуры, которая находит применение в теории графов, машинном обучении и других областях.

Некоторый дальнейший прогресс в этом направлении почти неизбежен, но есть пределы. В 2015 году Ле Галль и двое его соавторов доказали, что нынешний подход — лазерный метод в сочетании с алгоритмом Копперсмита-Винограда — не может дать омегу ниже 2,3078. Чтобы внести какие-либо дальнейшие улучшения, сказал Ле Галль, «необходимо улучшить первоначальный подход Копперсмита и Винограда, который практически не изменился с 1987 года». Но пока лучшего способа никто не придумал. Возможно, его даже не будет.

«Улучшение омеги на самом деле является частью понимания этой проблемы, — сказал Чжоу. — Если мы сможем хорошо понять проблему, мы сможем разработать для неё лучшие алгоритмы. И мы всё ещё находимся на самых ранних этапах понимания этой старой проблемы».

Автор перевода @arielf

НЛО прилетело и оставило здесь промокод для читателей нашего блога:
-15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS.