Disclaimer Данная статья публикуется исключительно в ознакомительных целях, за использование материалов, опубликованных в данной статье автор ответственности не несет.
Так же хочу сразу предупредить, что если вы рассчитываете найти в этой статье пошаговое руководство к прослушиванию GSM трафика или надеетесь, прочитав данную статью, получить доступ к телефонным разговорам ваших друзей, знакомых, домашних животных, то лучше проигнорируйте ее. Здесь вы не найдете ничего интересного. Нет правда, не ходите под кат, там скука.
Часть 1: основные моменты GSM безопасности
Прежде чем приступить к описанию алгоритма шифрования используемого в GSM сетях рассмотрим каким образом происходит аутентификация пользователя и формирования ключа шифрования. Для этого воспользуемся картинкой, позаимствованной с википедии(за качество прошу прощения, не нашел ничего лучше).
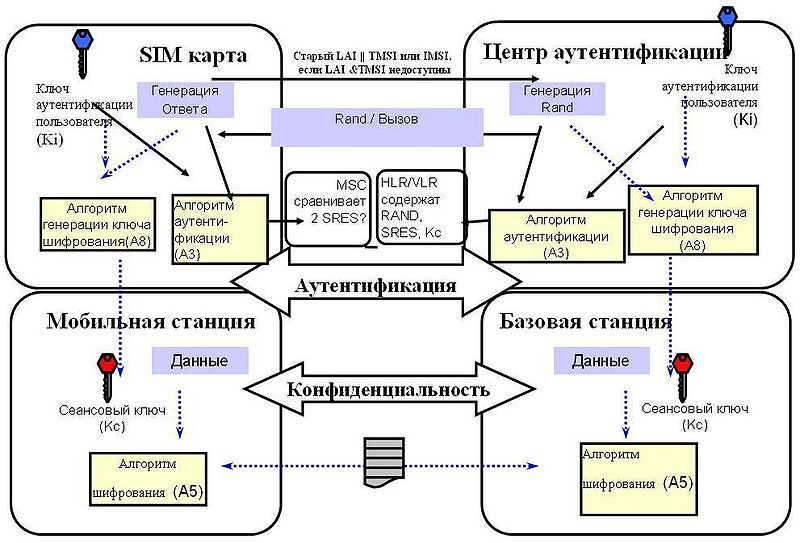
На данном рисунке схематично представлены следующие шаги:
- Телефон оператора подключается к сети.
- Для подтверждения своей подлинности телефон посылает специальный идентификационный код, называемый TMSI(Temporary Mobile Subscriber Identity).
- Центр Аутентификации(ЦА) генерирует 128-битное случайное число RAND и посылает его на Мобильную Станцию(МС).
- МС зашифровывает полученное число RAND, используя свой секретный ключ Ki и алгоритм аутентификации A3.
- MC берет первые 32 бита из последовательности, полученной на предыдущем шаге(назовем их SRES(signed response)) и отправляет их обратно на ЦА.
- ЦА проделывает ту же операцию и получает 32 битную последовательность XRES(expected response).
- После чего ЦА сравнивает SRES и XRES. В случае, если оба значения равны, телефон считается аутентифицированным.
- МС и ЦА вычисляют сессионный ключ шифрования, используя секретный ключ Ki и алгоритм формирования ключа A8 Kc=A8ki(RAND)
Говоря об алгоритмах аутентификации A3 и алгоритме формирования ключа A8, следует отметить что на практике большинство сотовых операторов используют для этих целей один алгоритм, называемый COMP128(он имеет множество модификаций COMP128-1, COMP128-2, COMP128-3).
COMP128 представляет собой обыкновенную хэш-функцию, на входе которая принимает 128-битную последовательность и на выходе возвращает 96-битную.
Так вот, вместо применения разных алгоритмов для аутентификации и формирования сессионного ключа применяется следующая схема:
SRES=Первые 32 бита от COMP128(Ki||RAND)
Kс=Последние 64 бита COMP128(Ki||RAND).
Как всегда в криптографии, попытка сэкономить время разработчикам обернулась полным провалом. Безопасность GSM сетей изначально основывалась на принципе «безопасность за счёт неизвестности». И когда в 1998 году алгоритм был вскрыт группой исследователей состоящих из Marc Briceno, Ian Goldberg и David Wagner обранужился одна занятная особенность: последние 10 бит секретного ключа Ki всегда равнялись нулю. Используя это любопытное свойство, а так же уязвимость COMP128 к «атаке дней рождений» Marc Briceno, Ian Goldberg и David Wagner смогли извлечь секретный ключ Ki из SIM-карты.
Результатом этого исследования стал повсеместный отказ от алгоритма COMP128 и его замена на более надежные модификации COMP128-2 и COMP128-3, технические детали которых держатся в тайне. Хм… вам это ничего не напоминает?
Часть 2: алгоритм шифрования A5/1
Давайте теперь перейдем от вещей более общих к вещам более частным и поговорим о том как в GSM реализовано шифрование телефонных разговоров.
В качестве алгоритма шифрования в GSM используются алгоритмы из семейства A5. На сегодняшний день их всего 3:
- A5/1 — поточный шифр, наиболее распространенный на сегодня.
- A5/2-вариант предыдущего алгоритма «для бедных». Очень похож на своего «старшего брата», но изначально задумывался, как сильно ослабленная версия A5/1. В настоящее время не используется
- A5/3-блочный шифр. Разработан в 2002 году с целью заменить устаревший A5/1. Однако в настоящее время используется только в 3GPP сетях. У алгоритма найден ряд уязвимостей, но о практических атаках речи пока не идет.
Рассмотрим подробнее алгоритм A5/1.
Итак, как уже было сказано выше A5/1 это поточный шифр. И вновь на помощь спешит картинка с википедии:
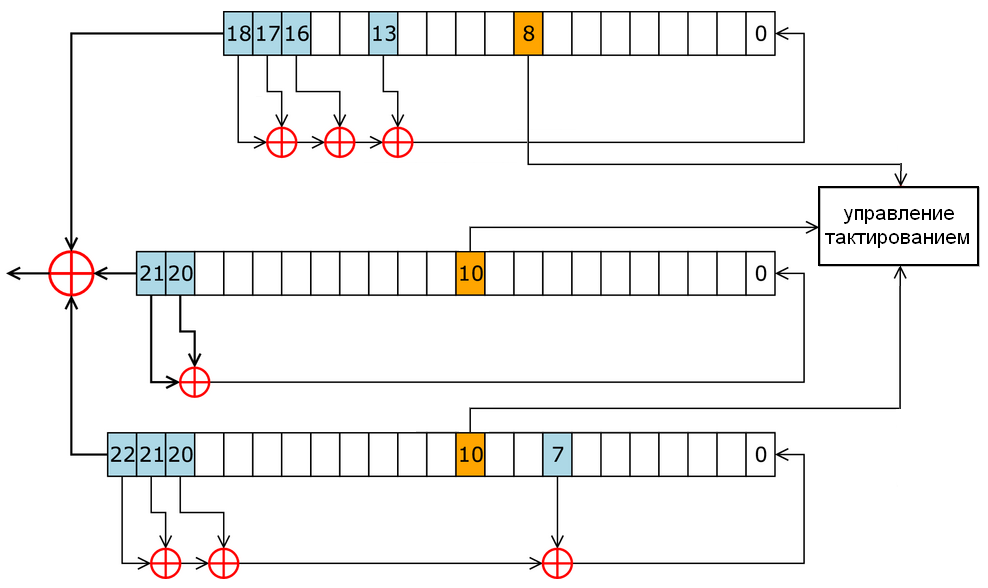
Внутреннее состояние шифра A5/1 состоит из трех линейных регистров сдвига с обратной связью R1, R2, R3, длиной 19, 22 и 23 бита соответственно(всего 64 бита).
Сдвиг в регистрах R1, R2, R3 происходит только при выполнении определенного условия. Каждый регистр содержит " бит управления тактированием". В R1 это 8-й бит, а в R2 и R3 — 10-й. На каждом шаге сдвигаются только те регистры у которых значение бита синхронизации равно большинству значений синхронизирующих битов всех трех регистров.
Перед работой алгоритма выполняется инициализация регистров. Происходит это следующим образом:
- R1=R2=R3=0
- For i=0 to 63 do
R1[0]=R1[0]⊕Kc[i]
R2[0]=R2[0]⊕Kc[i]
R2[0]=R2[0]⊕Kc[i]
Сдвинуть все регистры на одну позицию, игнорируя биты синхронизации. - For i=0 to 22 do
R1[0]=R1[0]⊕FrameCount[[i]
R2[0]=R2[0]⊕FrameCount[[i]
R2[0]=R2[0]⊕FrameCount[[i]
Сдвинуть все регистры на одну позицию, игнорируя биты синхронизации. - For i=0 to 99 do
Сдвинуть регистры на одну позицию, с учетом битов синхронизации.
Где FrameCount 32-х битная запись номера текущего фрейма.
После инициализации производится вычисление 228 бит выходной последовательности. 114 бит используется для шифрования данных исходящего из сети к мобильному телефону, остальные 114 бит для шифрования данных идущих от телефона к сети. Само шифрование представляет собой обыкновенный XOR между данными и произведенным алгоритмом A5/1 ключевым потоком.
После передачи данных номер фрейма увеличивается на единицу и заново производится инициализация регистров.
Воспользуемся приведенным выше описанием и реализуем шифрование A5/1 на С#.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Collections;
namespace A5project
{
class A5Enc
{
private bool[] reg = new bool[19];
private bool[] reg2 = new bool[22];
private bool[] reg3 = new bool[23];
//конструктор, который позволяет сразу установить начальное состояние регистров и нужное значение
public A5Enc(bool[][] startState)
{
reg = startState[0];
reg2 = startState[1];
reg3 = startState[2];
}
public A5Enc()
{
for (int i = 0; i < 19; i++)
reg[i] = false;
for (int i = 0; i < 22; i++)
reg2[i] = false;
for (int i = 0; i < 23; i++)
reg3[i] = false;
}
//нормальная инициализация регистров, используется при обычном вызове метода A5
public void KeySetup(byte[] key, int[] frame)
{
for (int i = 0; i < 19; i++)
reg[i] = false;
for (int i = 0; i < 22; i++)
reg2[i] = false;
for (int i = 0; i < 23; i++)
reg3[i] = false;
BitArray KeyBits = new BitArray(key);
BitArray FrameBits = new BitArray(frame);
bool[] b = new bool[64];
for (int i = 0; i < 64; i++)
{
clockall();
reg[0] = reg[0] ^ KeyBits[i];
reg2[0] = reg2[0] ^ KeyBits[i];
reg3[0] = reg3[0] ^ KeyBits[i];
}
for (int i = 0; i < 22; i++)
{
clockall();
reg[0] = reg[0] ^ FrameBits[i];
reg2[0] = reg2[0] ^ FrameBits[i];
reg3[0] = reg3[0] ^ FrameBits[i];
}
for (int i = 0; i < 100; i++)
{
clock();
}
}
//частичная инициализация, в регистры грузится только номер фрейма
public void KeySetup(int[] frame)
{
BitArray FrameBits = new BitArray(frame);
for (int i = 0; i < 22; i++)
{
clockall();
reg[0] = reg[0] ^ FrameBits[i];
reg2[0] = reg2[0] ^ FrameBits[i];
reg3[0] = reg3[0] ^ FrameBits[i];
}
for (int i = 0; i < 100; i++)
{
clock();
}
}
private void clock()
{
bool majority = ((reg[8] & reg2[10]) | (reg[8] & reg3[10]) | (reg2[10] & reg3[10]));
if (reg[8] == majority)
clockone(reg);
if (reg2[10] == majority)
clocktwo(reg2);
if (reg3[10] == majority)
clockthree(reg3);
}
//набор функций реализующих сдвиги регистров
private bool[] clockone(bool[] RegOne)
{
bool temp = false;
for (int i = RegOne.Length - 1; i > 0; i--)
{
if (i == RegOne.Length - 1)
temp = RegOne[13] ^ RegOne[16] ^ RegOne[17] ^ RegOne[18];
RegOne[i] = RegOne[i - 1];
if (i == 1)
RegOne[0] = temp;
}
return RegOne;
}
private bool[] clocktwo(bool[] RegTwo)
{
bool temp = false;
for (int i = RegTwo.Length - 1; i > 0; i--)
{
if (i == RegTwo.Length - 1)
temp = RegTwo[20] ^ RegTwo[21];
RegTwo[i] = RegTwo[i - 1];
if (i == 1)
RegTwo[0] = temp;
}
return RegTwo;
}
private bool[] clockthree(bool[] RegThree)
{
bool temp = false;
for (int i = RegThree.Length - 1; i > 0; i--)
{
if (i == RegThree.Length - 1)
temp = RegThree[7] ^ RegThree[20] ^ RegThree[21] ^ RegThree[22];
RegThree[i] = RegThree[i - 1];
if (i == 1)
RegThree[0] = temp;
}
return RegThree;
}
private void clockall()
{
reg = clockone(reg);
reg2 = clocktwo(reg2);
reg3 = clockthree(reg3);
}
//метод возвращающий 114 бит сгенерированного потока
public bool[] A5()
{
bool[] FirstPart = new bool[114];
for (int i = 0; i < 114; i++)
{
clock();
FirstPart[i] = (reg[18] ^ reg2[21] ^ reg3[22]);
}
return FirstPart;
}
//метод возвращающий всю 228 битную последовательность сгенерированного потока
public bool[] A5(bool AsFrame)
{
bool[] FirstPart = new bool[228];
for (int i = 0; i < 228; i++)
{
clock();
FirstPart[i] = (reg[18] ^ reg2[21] ^ reg3[22]);
}
return FirstPart;
}
public byte[] FromBoolToByte(bool[] key, bool lsb)
{
int bytes = key.Length / 8;
if ((key.Length % 8) != 0) bytes++;
byte[] arr2 = new byte[bytes];
int bitIndex = 0, byteIndex = 0;
for (int i = 0; i < key.Length; i++)
{
if (key[i])
{
if(lsb)
arr2[byteIndex] |= (byte)(((byte)1) << (7 - bitIndex));
else
arr2[byteIndex] |= (byte)(((byte)1) << (bitIndex));
}
bitIndex++;
if (bitIndex == 8)
{
bitIndex = 0;
byteIndex++;
}
}
return arr2;
}
}
}
Проверить правильность кода можно, запустив программу с ключом {0x12, 0x23, 0x45, 0x67, 0x89, 0xAB, 0xCD, 0xEF} и номером фрейма 0x134. Две сгенерированные последовательности по 114 бит каждая, должны быть равны соответственно { 0x53, 0x4E, 0xAA, 0x58, 0x2F, 0xE8, 0x15, 0x1A, 0xB6, 0xE1, 0x85, 0x5A, 0x72, 0x8C, 0x00 } и { 0x24, 0xFD, 0x35, 0xA3, 0x5D, 0x5F, 0xB6, 0x52, 0x6D, 0x32, 0xF9, 0x06, 0xDF, 0x1A, 0xC0 }.
Именно такие тестовые данные использовали Marc Briceno, Ian Goldberg и David Wagner в своей самой первой реализации алгоритма, написанной на С.
Функция шифрования/расшифровки, использующая данный класс, будет выглядеть следующим образом:
private byte[] A5Encyptor(bool[] msg,byte[] key)
{
A5Enc a5 = new A5Enc();
int[] frame = new int[1];
bool[] resbits = new bool[msg.Count];
int framesCount = msg.Length / 228;
if ((msgbits.Length % 228) != 0)
framesCount++;
for (int i = 0; i < framesCount; i++)
{
frame[0] = i;
a5.KeySetup(key, frame);
bool[] KeyStream = a5.A5(true);
for (int j = 0; j < 228; j++)
{
resbits[i * 228 + j] = msgbits[i * 228 + j] ^ KeyStream[j];
}
}
return a5.FromBoolToByte(resbits, false);
}
Теперь когда у нас есть функция, позволяющая шифровать и расшифровывать данные, давайте поговорим об уязвимостях алгоритма A5/1.
На сегодняшний день известно большое количество успешных атак на GSM шифрование и все они относятся к атакам типа known-plaintext, т.е. для восстановления ключа атакующему помимо зашифрованных фреймов необходимо знать так же незашифрованные данные, которые соответствуют этим фреймам. На первый взгляд такое требование может показаться фантастическим, однако из-за специфики стандарта GSM, в котором помимо голосового трафика передаются различные системные сообщения, такого рода атаки из разряда теоретических переходят в разряд практических. Системные сообщения GSM содержат повторяющиеся данные и могут использоваться злоумышленником. В частности метод, предложенный Karsten Nohl в 2010 году основан как раз таки на поиске такого рода данных в шифротексте и простом переборе различных вариантов ключей, хранящихся в радужных таблицах, до тех пор пока не будет найден ключ, порождающий нужный шифротекст для известного заранее системного сообщения.
Часть 3: атака на алгоритм A5/1
Однако же у нас нет огромных ресурсов, необходимых для вычисления радужных таблиц, поэтому мы реализуем атаку попроще, относящуюся к т.н. «корреляционным атакам».
Расматриваеммая нами атака была впервые описана в 2002 году двумя исследователями: Patrik Ekdahl и Thomas Johansson.
Из определения процедуры инициализации можно заключить, что начальное состояние регистров является линейной функцией от сессионного ключа K и номера фрейма Fn.
Зная так же, что выходной бит генератора является XOR-ом выходных бит всех трех регистров мы можем записать следующее равенство:
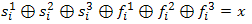(1),
где si-последовательность генерируемая регистрами после загрузки в них только битов ключа K. fi-последовательность, после загрузки только битов номера фрейма, а x-выходной бит регистра.
Так же из определения инициализации мы знаем, что первые 100 циклов алгоритм работает «в холостую», т.е. не производит никаких выходных битов, и первый бит выходной последовательности на самом деле является 101-м сгенерированным битом. Таким образом, если учесть, что на каждом шаге вероятность сдвига для каждого регистра равняется 3/4, можно сделать предположение, что после 101 шага, каждый регистр сдвигался ровно 76 раз. Следовательно, формула (1) преобразуется в:
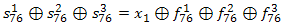(2)
Обозначив правую часть (2) как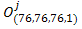 
перепишем формулу:
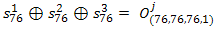(3)
Т.к. выражение в правой части (3) нам известно, мы получаем 1 бит информации о ключевой последовательности S, а именно о состоянии 76-й позиции каждого регистра после инициализации. Действуя подобным образом, мы можем предположить, что на 102 позиции R1 остался также на позиции 76, а регистры R2 и R3 сдвинулись на позицию 77, таким образом мы получаем информацию о 77-й позиции регистра, и т.д. Всего нам необходимо вскрыть 64 бита, для успешного восстановления начального состояния.
Разумеется ситуация (76,76,76) возникает именно на 101 шаге с крайне низкой вероятностью, и если бы мы решили действовать подобным образом, то нам понадобилось бы перебрать огромное количество фреймов, пока наконец не попадется именно тот, в котором после 101 сдвига каждый регистр прокрутился на 76 позиций. Для того, чтобы уменьшить необходимое количество фреймов Ekdahl и Johansson предложили следующий метод.
Нет нужды угадывать конкретную позицию в которой регистры проворачиваются (cl1,cl2,cl3) раз. Достаточно просто знать, что с большой долей вероятности каждый регистр провернется от 76 до 102 на отрезке I=[100,140] выходных бит каждого фрейма.
Таким образом, для каждого фрейма мы можем вычислить вероятность: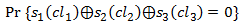 
как
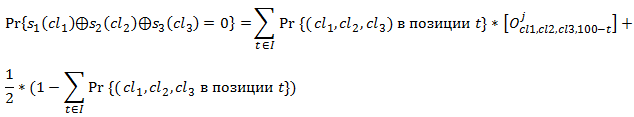(4),
где
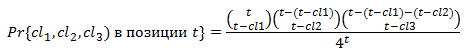
и обозначает вероятность того, что t-й бит был порожден позициями регистров (cl1, cl2, cl3).
Вычислив (4) для каждого доступного фрейма усредним полученные вероятности при помощи логарифма:
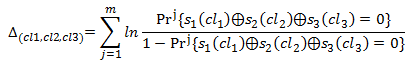(5).
Если (5)> 0, значит s1(cl1)⊕s2(cl2)⊕s3(cl3)=0, в противном случае s1(cl1)⊕s2(cl2)⊕s3(cl3)=1.
Опишем атаку полностью в виде алгоритма:
- Выбираем интервал C. Напимер С=[79,86]
- Пусть переменные cl1,cl2,cl3 пробегают все значения из интервала C, для каждого фрейма вычисляем (4)
- Для всех полученный значений вычисляем (5)
- На основании значения Δ выбираем значение s1(cl1)⊕s2(cl2)⊕s3(cl3)
Результатом выполнения данного алгоритма будут 512 уравнений вида s1(79)⊕s2(79)⊕s3(79)=0, состоящие из 8 неизвестных. Решив эту систему уравнений простым перебором, мы получим по 8 бит начального значения каждого регистра.
Повторив алгоритм еще два раза для интервалов [87, 94] и [95, 102] мы получим по 24 бита начального состояния каждого из регистров. Этого нам более чем достаточно. Прокрутим каждый из регистров 101 раз назад мы получим как раз то состояние регистров, которое было после второго шага инициализации, т.е. после загрузки в регистры ключевых битов. И теперь мы можем сгенерировать всю ключевую последовательность целиком.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Collections;
namespace A5project
{
class A5attack
{
private double[] factorials = new double[150];
//Вычисление Pr(cl1,cl2,cl3 в позиции v)
private double PinVth(int cl1, int cl2, int cl3, int v)
{
double y=0;
double x = 0;
double z = 0;
double w = 0;
if((v - (v - cl1) - (v - cl2) - (v - cl3))>=0)
y=factorials[v - (v - cl1) - (v - cl2) - (v - cl3)];
else
y=1;
if ((v - cl1) >= 0)
x = factorials[v - cl1];
else
x = 1;
if ((v - cl3) >= 0)
z = factorials[v - cl3];
else
z = 1;
if ((v - cl2) >= 0)
w = factorials[v - cl2];
else
w = 1;
double a = factorials[v] / (x * factorials[v - (v - cl1)]);
double b = factorials[v - (v - cl1)] / (w * factorials[v - (v - cl1) - (v - cl2)]);
double c = factorials[v - (v - cl1) - (v - cl2)] / (z * y);
double d = Math.Pow(4, v);
return (a * b * c) / d;
}
private double factorial(int x)
{
double result=1;
for (int i = x; i > 1; i--)
result = result * i;
return result;
}
private bool[] reg = new bool[19];
private bool[] reg2 = new bool[22];
private bool[] reg3 = new bool[23];
//неполная инициализация, предполагается что ключевые биты уже загруженные в регистры
public void KeySetup(int[] frame)
{
for (int i = 0; i < 19; i++)
reg[i] = false;
for (int i = 0; i < 22; i++)
reg2[i] = false;
for (int i = 0; i < 23; i++)
reg3[i] = false;
BitArray FrameBits = new BitArray(frame);
for (int i = 0; i < 22; i++)
{
clockall();
reg[0] = reg[0] ^ FrameBits[i];
reg2[0] = reg2[0] ^ FrameBits[i];
reg3[0] = reg3[0] ^ FrameBits[i];
}
}
//процедуры по управлению сдвигами регистров
private void clock()
{
bool majority = ((reg[8] & reg2[10]) | (reg[8] & reg3[10]) | (reg2[10] & reg3[10]));
if (reg[8] == majority)
clockone(reg);
if (reg2[10] == majority)
clocktwo(reg2);
if (reg3[10] == majority)
clockthree(reg3);
}
private bool[] clockone(bool[] RegOne)
{
bool temp = false;
for (int i = RegOne.Length - 1; i > 0; i--)
{
if (i == RegOne.Length - 1)
temp = RegOne[13] ^ RegOne[16] ^ RegOne[17] ^ RegOne[18];
RegOne[i] = RegOne[i - 1];
if (i == 1)
RegOne[0] = temp;
}
return RegOne;
}
private bool[] clocktwo(bool[] RegTwo)
{
bool temp = false;
for (int i = RegTwo.Length - 1; i > 0; i--)
{
if (i == RegTwo.Length - 1)
temp = RegTwo[20] ^ RegTwo[21];
RegTwo[i] = RegTwo[i - 1];
if (i == 1)
RegTwo[0] = temp;
}
return RegTwo;
}
private bool[] clockthree(bool[] RegThree)
{
bool temp = false;
for (int i = RegThree.Length - 1; i > 0; i--)
{
if (i == RegThree.Length - 1)
temp = RegThree[7] ^ RegThree[20] ^ RegThree[21] ^ RegThree[22];
RegThree[i] = RegThree[i - 1];
if (i == 1)
RegThree[0] = temp;
}
return RegThree;
}
private void clockall()
{
reg = clockone(reg);
reg2 = clocktwo(reg2);
reg3 = clockthree(reg3);
}
//вычисление возвращаемого бита, когда регистры находятся в положениях cl1, cl2 и cl3
public bool Oj(int cl1,int cl2, int cl3)
{
for (int i = 0; i < cl1; i++)
{
clockone(reg);
}
for (int i = 0; i < cl2; i++)
{
clocktwo(reg2);
}
for (int i = 0; i < cl3; i++)
{
clockthree(reg3);
}
return (reg[18] ^ reg2[21] ^ reg3[22]);
}
//Вероятность того, что для данного фрейма XOR выходных битов регистра равен нулю
public double Pj(int cl1, int cl2, int cl3, int j, bool[] frame)
{
double result = 0;
double rightPart = 0;
int[] framenumb=new int[1]{j};
KeySetup(framenumb);
bool[] tempReg = new bool[19];
bool[] tempReg2 = new bool[22];
bool[] tempReg3 = new bool[23];
Array.Copy(reg, tempReg, 19);
Array.Copy(reg2, tempReg2, 22);
Array.Copy(reg3, tempReg3, 23);
bool FramesBit = Oj(cl1, cl2, cl3);
for (int i = 100; i < 100 + 50; i++)
{
Array.Copy(tempReg, reg, 19);
Array.Copy(tempReg2, reg2, 22);
Array.Copy(tempReg3, reg3, 23);
double temp = PinVth(cl1, cl2, cl3, i);
rightPart += temp;
if((FramesBit^frame[i-100])==false)
temp=temp*1;
else
temp=0;
result += temp;
}
result = result + ((1 - rightPart) / 2);
return result;
}
//Общая вероятность того, что биты cl1, cl2, cl3 в сумме дают 0. Если >0 тогда значение записывается как 0
//в другом случае, как 1
public double LikehoodRatio(int cl1, int cl2, int cl3, bool[] keystream)
{
double result = 0;
for (int i = 0; i < keystream.Length/228; i++)
{
bool[] temp=new bool[228];
Array.Copy(keystream,i*228,temp,0,228);
double x=Pj(cl1, cl2, cl3, i, temp);
result = result + Math.Log(( x/ (1 - x)));
}
return result;
}
public bool FindKeyBit(int cl1, int cl2, int cl3, bool[] keystream)
{
for (int i = 0; i < 150; i++)
factorials[i] = factorial(i);
if (LikehoodRatio(cl1, cl2, cl3, keystream) >= 0)
return false;
else
return true;
}
//Загружает в регистры полученные биты и восстанавливае начальное значение
public bool[][] checkSol(byte[] first, byte[] second, byte[] third)
{
byte[] newFirst = new byte[3];
newFirst[0] = first[0];
newFirst[1] = second[0];
newFirst[2] = third[0];
byte[] newSecond = new byte[3];
newSecond[0] = first[1];
newSecond[1] = second[1];
newSecond[2] = third[1];
byte[] newThird = new byte[3];
newThird[0] = first[2];
newThird[1] = second[2];
newThird[2] = third[2];
bool[] firstArr1 = new BitArray(newFirst).Cast<bool>().ToArray().Reverse().ToArray();
bool[] firstArr = new bool[19];
Array.Copy(firstArr1, 5, firstArr, 0, 19);
bool[] secondArr1 = new BitArray(newSecond).Cast<bool>().ToArray().Reverse().ToArray();
bool[] secondArr = new bool[22];
Array.Copy(secondArr1, 2, secondArr, 0, 22);
bool[] thirdArr1 = new BitArray(newThird).Cast<bool>().ToArray().Reverse().ToArray();
bool[] thirdArr = new bool[23];
Array.Copy(thirdArr1, 1, thirdArr, 0, 23);
for (int i = 0; i < 101; i++)
{
BackClockone(firstArr);
}
for (int i = 0; i < 101; i++)
{
BackClocktwo(secondArr);
}
for (int i = 0; i < 101; i++)
{
BackClockthree(thirdArr);
}
bool[][] result = new bool[3][];
result[0] = firstArr;
result[1] = secondArr;
result[2] = thirdArr;
return result;
}
private void BackClockone(bool[] RegOne)
{
bool temp = false;
for (int i = 0; i < RegOne.Length-1; i++)
{
if (i == 0)
temp = RegOne[0];
RegOne[i] = RegOne[i+1];
if (i == (RegOne.Length-2))
RegOne[RegOne.Length - 1] = temp ^ RegOne[13] ^ RegOne[16] ^ RegOne[17];
}
}
private void BackClocktwo(bool[] RegTwo)
{
bool temp = false;
for (int i = 0; i < RegTwo.Length-1; i++)
{
if (i == 0)
temp = RegTwo[0];
RegTwo[i] = RegTwo[i + 1];
if (i == (RegTwo.Length-2))
RegTwo[RegTwo.Length - 1] = temp ^ RegTwo[20];
}
}
private void BackClockthree(bool[] RegThree)
{
bool temp = false;
for (int i = 0; i < RegThree.Length-1; i++)
{
if (i == 0)
temp = RegThree[0];
RegThree[i] = RegThree[i + 1];
if (i == (RegThree.Length-2))
RegThree[RegThree.Length - 1] = temp ^ RegThree[7] ^ RegThree[20] ^ RegThree[21];
}
}
}
}
Используя функцию FindKeyBit следующим образом:
private bool[] attack()
{
bool[] keypart=new bool[512];
int count = 0;
A5attack tryattack = new A5attack();
for(int i=79; i<87;i++)
for(int j=79; j<87; j++)
for (int k = 79; k < 87; k++)
{
bool temp=tryattack.FindKeyBit(i, j, k, keystream);
int time = finish - start;
keypart[count] = temp;
count++;
}
return keypart;
}
мы получим массив из 512 значений в котором записаны XOR ключевых бит начиная с позиции 79 по позицию 86.
Получив все 24 бита из каждого регистра, и переведя их в байтовые массивы проверяем наше решение:
Private void checkSolution()
{
A5attack LetsAttack = new A5attack();
int[] testframe = new int[1] { 0 };
bool[][] startState = LetsAttack.checkSol(first, second, third);
A5Enc a5check = new A5Enc(startState);
bool[] TempFrame = new bool[228];
a5check.KeySetup(testframe);
TempFrame = a5check.A5(true);
for (int l = 0; l < 228; l++)
{
find = true;
if (keystream[l] != TempFrame[l])
{
find = false;
break;
}
}
}
Если полученный фрейм совпадает с первым фреймом известного ключевого потока, значит атака была реализована успешно и мы вскрыли сеансовый ключ алгоритма A5/1.
Часть 4: заключительная
Подводя итог, хочу отметить что описанная атака является одной из первых подобных атака. Наиболее совершенная из них позволяет с 90% вероятностью вскрыть сеансовый ключ из всего 2000 фреймов(9 секунд разговора).
И хотя практическое применение такого рода атака весьма сомнительно, следует понимать, что как криптографический примитив алгоритм A5/1 фатально уязвим перед plaintext-attack.
Литература и ссылки
- Marcin Olawski. «Security in the GSM network».
- Patrik Ekdahl and Thomas Johansson. «Another Attack on A5/1».
- Karsten Nohl. «Attacking phone privacy».
- Marc Briceno, Ian Goldberg, and David Wagner. A pedagogical implementation of A5/1.
PS: автор будет признателен, если кто-нибудь поделится работой Barkan, Elad; Eli Biham (2005). «Conditional Estimators: An Effective Attack on A5/1». В ней описывается атака, которую я упомянул в заключительной части.
Автор: NeverWalkAloner
