Ускоряем приложение: никаких фреймворков — только математика

Представьте, что вам нужно ускорить работу огромной легаси-системы с 50 микросервисами, нагрузка на которую выросла в 2000 раз. При этом она обрабатывает затратные по времени операции, которые зависят друг от друга в плане данных. 

Первыми на ум приходят стандартные подходы к оптимизации, например внедрить кэширование или улучшить работу с базой. Но я расскажу вам про более необычный, математический способ — алгоритм сетевого планирования. Он помогает составлять технологические карты и находить узкие места в процессах с высокой степенью параллелизма.

Меня зовут Игорь Чирков, я кандидат физико-математических наук и в прошлом преподаватель. Сейчас работаю в Почтатехе главным Java-разработчиком на проекте «Отправка». Об этом сервисе и пойдет рассказ. 

Как росло приложение

Приложение «Отправка» как проект появилось в 2015 году на смену старому десктопному клиенту. Изначально оно позволяло интернет-магазинам удаленно оформлять обыкновенные посылки, чтобы потом просто сдавать их в почтовое отделение. Первая версия попала в прод весной 2016 года.

Приложение стремительно набирало популярность: клиенты быстро перешли на него с десктопной версии. Начал добавляться функционал, приложение интегрировали с другими сервисами Почты России. Нагрузка росла, но постепенно. 

Перелом произошел, когда в приложении запустили отправку писем. Эта функция привлекла действительно крупных клиентов, которые генерируют большой поток отправлений. В итоге нагрузка выросла в 2000 раз. 

К этому моменту система уже сильно разрослась, добавилось много смежных функций, а еще приложение стало точкой входа для других почтовых сервисов. Существенно изменить архитектуру под новую нагрузку уже было невозможно.

Структура сервисов

У нас микросервисное приложение, построенное на  REST. На все сервисы можно посмотреть как на системы массового обслуживания. У каждого будет примерно такая структура:

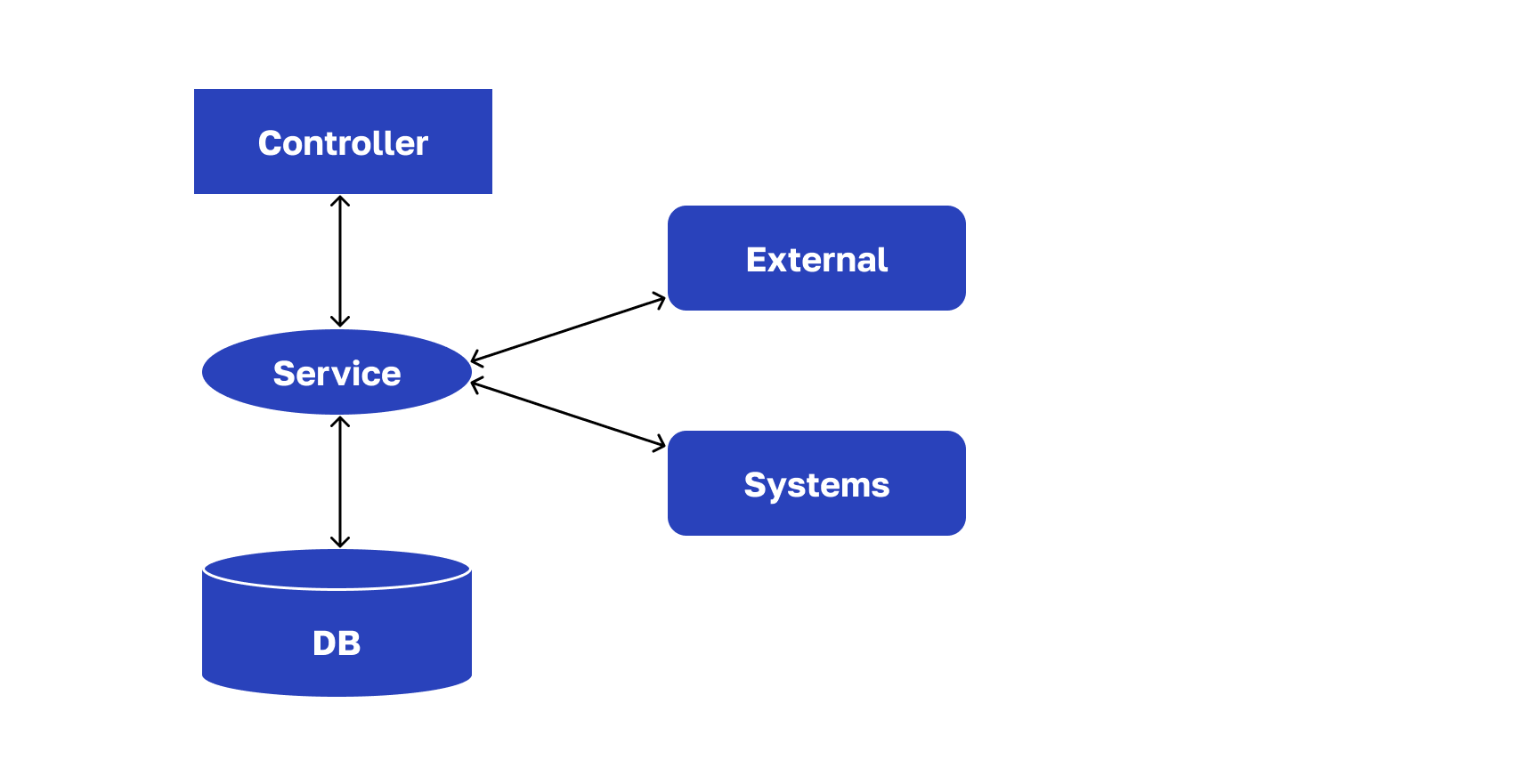
В системах массового обслуживания есть два самых важных параметра:

1. Скорость входящей очереди.

2. Скорость обслуживания единичных сообщений.

Они определяют то, как работают сервисы. Представим, что входящие сообщения поступают довольно быстро, а обслуживающий механизм вялый (будем сначала считать, что он единственный). Понятно, что в таком случае очередь будет копиться и, теоретически, расти бесконечно. Это приведет к потере некоторых сообщений — они не будут обрабатываться.

Проблему можно решить с помощью масштабирования: подключить несколько серверов, докинуть инстансы микросервиса и роутить входящие сообщения между ними. Но этот подход хорошо работает при асинхронном процессе: когда вы не отвечаете на запросы сразу, а что-то пишете в базу, и потом пользователь это когда-нибудь увидит. Но если требуется синхронный ответ, то придется отдельно поработать с производительностью микросервисов.

Анализируем курьерский микросервис

Разберем один из наших микросервисов, который отвечает за взаимодействие с курьерской службой. У него несколько методов, и один был довольно тормозной. 

Проблема с кодом класса

У  микросервиса была следующая структура:

• Слой контроллера, который принимает запрос

• Сервисный слой, где сосредоточена логика обработки запроса

• Периферийная структура, представленная БД и внешними системами, которых не две, как нарисовано на схеме выше, а примерно десяток. При этом не все системы принадлежат нашему контуру — некоторые внешние

Структура простая, и все было бы хорошо, если бы не один момент: код класса, который представлял сервисный слой, был плохо структурирован и содержал порядка 2000 строк и кучу приватных методов. Поэтому было непонятно, где что менять.

Разбираемся в логике сервиса

Что делать в этой ситуации? Я решил сначала разобраться с логикой сервиса. Поэтому представил его работу в виде комбинации отдельных операций (желательно бизнес-операций), а сам сервис — как оркестратор, который ими манипулирует. 

Каждую из операций представил в виде узкоспециализированного класса с единственным методом. Я не стал изначально менять логику работы сервиса, а просто сделал рефакторинг. В результате получил такую структуру:

На картинке линейный граф. В реальной жизни у него могут быть логические ветвления, но мы их опустим, чтобы не отвлекаться от сути.  

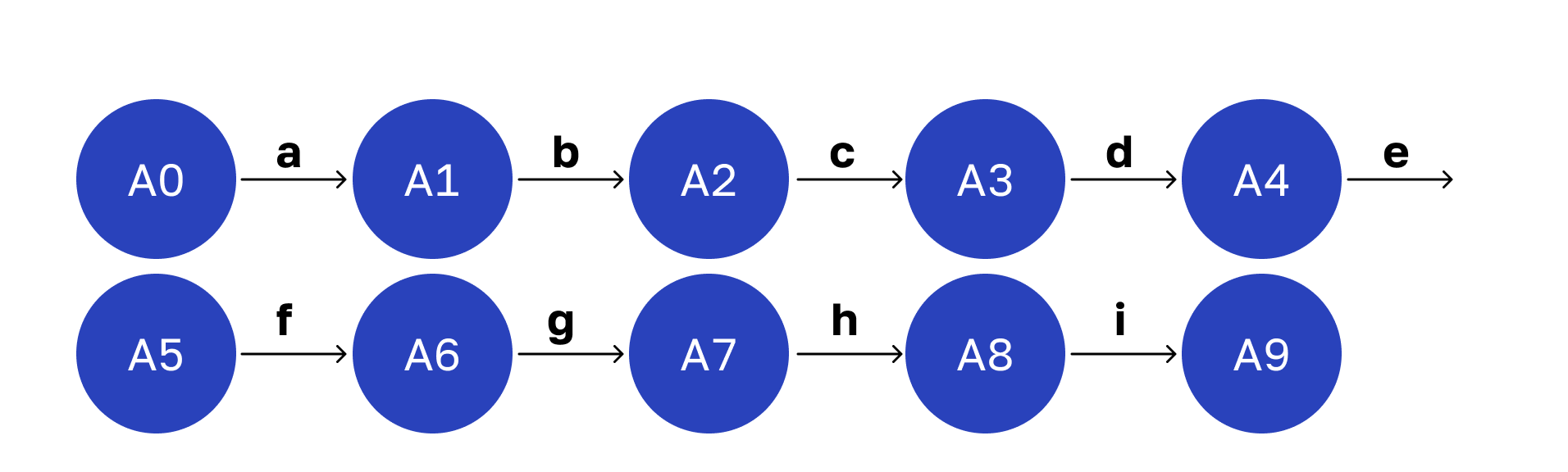
Классы — стрелки с латинскими буквами. Вершины графа обозначают состояние системы после выполнения той или иной операции. Начальная вершина — поступление запроса, а конечная — ответ после его обработки. Переходы между этими состояниями соответствуют выполнению наших операций. 

Такой граф помог улучшить читаемость кода, и я стал понимать, как все работает.

Настал момент разобраться с производительностью системы. Для этого нужны какие-то метрики.

Определяем среднее время выполнения операции

Думаю, многие сталкивались с тем, что один и тот же запрос к БД выполняется за разное время. Эта величина случайная. На нее влияет множество факторов, которые трудно учесть. Тем более это касается бизнес-операций, о которых мы говорили выше.

Классические случайные величины изучает теория вероятности. У нее есть понятие «матожидание» — характеристика, которая обычно вычисляется как интеграл. Смысл ее очень простой — это среднее значение случайной величины. 

Плохая новость заключается в том, что мы не можем в реальной ситуации, кроме самых простейших случаев, вычислить матожидание случайных величин. Для этого нужно полностью знать функцию распределения такой случайной величины.

Хорошая новость: есть несложные статистические методы, которые позволяют оценивать параметры распределения, в том числе и матожидание. Для этого чаще всего используют точечную оценку — так называемое «выборочное среднее».

Поэтому я не стал городить огород, а воспользовался библиотекой Speed4j. Она позволяет добавить несложную функциональность в метод класса и снять с него статистические характеристики, а именно «выборочное среднее». 

Я добавил соответствующую функциональность в код классов операций и выставил свое приложение в прод. Затем настроил логер и получил снимок статистики работы сервиса. Проанализировал этот лог-файл и дополнил наш граф:

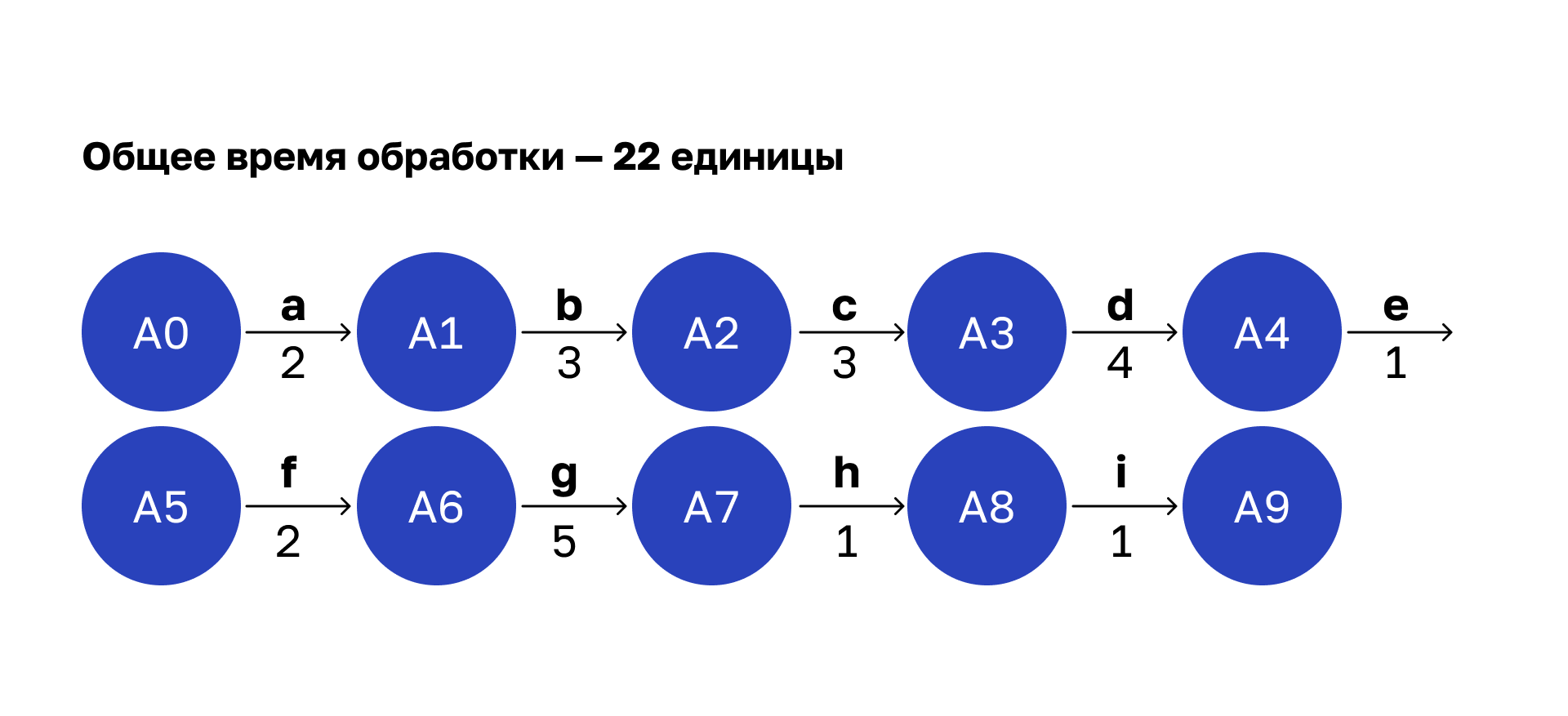
Числа под стрелочками обозначают условное время выполнения операции. В реальной жизни я измерял в миллисекундах, а здесь — в условных единицах.

Просуммируем время каждой операции и получим общее время обработки всего запроса — 22 единицы.

Выбираем способ оптимизации

Итак, у нас есть сервис, организованный как последовательное выполнение затратных по времени операций, которые зависят друг от друга. Я увидел три варианта, как ускорить его работу:

1. Оптимизировать выполнение отдельных операций.

Можно бороться за производительность каждой операции. Но этот путь не сулит больших перспектив. Почему? Во-первых, наш сервис обращается к внешним ресурсам, а на скорость обработки на той стороне мы повлиять не можем. И договориться с разработчиками внешних систем тоже не получится. Конечно, есть наши внутренние системы, но там, как правило, резерв небольшой.

2. Изменить структуру сервиса, перейти на многопоточную обработку.

Этот вариант более перспективный. Но в нашем процессе многие операции зависят от других в плане данных, поэтому распараллелить получится не всё. Нужна технологическая карта, чтобы выявить узкие места. 

3. Совместить первый и второй подходы: решить задачу сетевого планирования.

Мне пришло в голову, что я имею дело со знакомой ситуацией — задачей сетевого планирования. А значит, можно применить научные знания.

Оптимизируем с помощью алгоритма сетевого планирования

Распараллеливаем операции

Многопоточность получится внедрить там, где операции не зависят друг от друга в плане данных. Чтобы найти такие операции, построим карту зависимостей.

Состояние 0 — это поступление запроса на обработку, а стрелки — операции. Цифры под ними — время выполнения, которое мы вычислили выше с помощью Speed4j. 

Я выяснил, что операции a и b зависят только от входящих параметров. А значит, они могут стартовать сразу в момент поступления запроса. Их можно распараллелить. 

Добавим следующие два состояния и операции, которые происходят после них. 

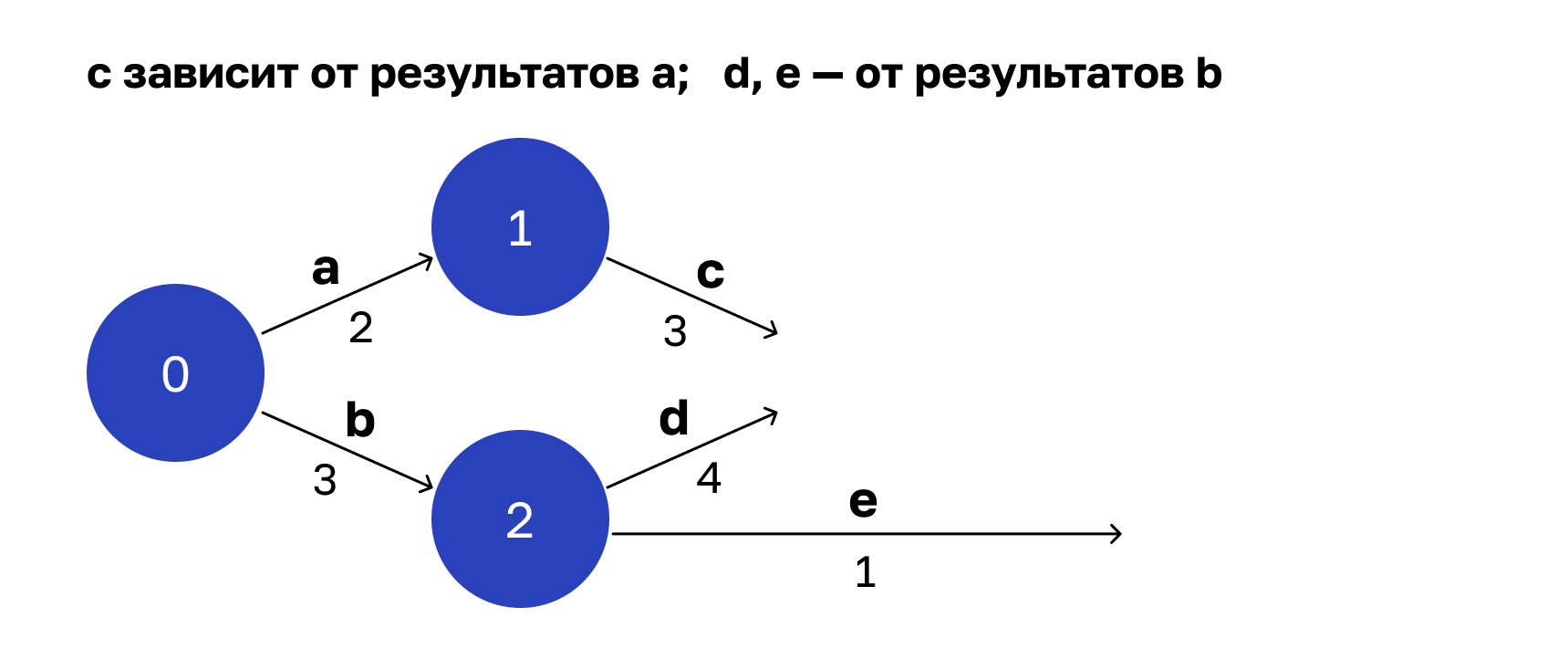
Здесь операция с ждет завершения а. Когда это произойдет, наступит состояние 1: операция a завершена, и может стартовать операция c. Операции d и e ждут завершения операции b. Значит, c, d, e тоже можно стартовать параллельно.

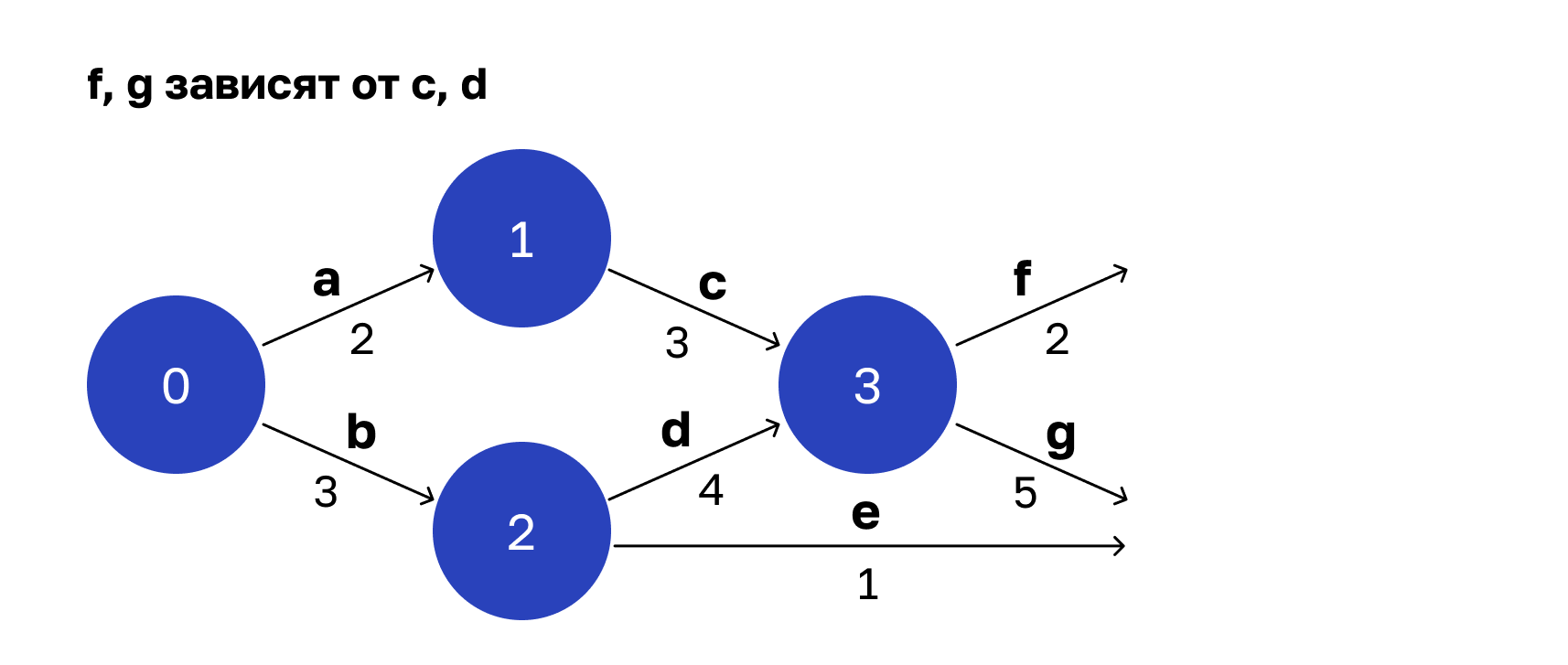
Дальше появляется вершина 3. Здесь операции f и g ждут завершения c и d. Завершению соответствует состояние 3, а из него исходят параллельные ребра — операции f и g.

Потом все аналогично.

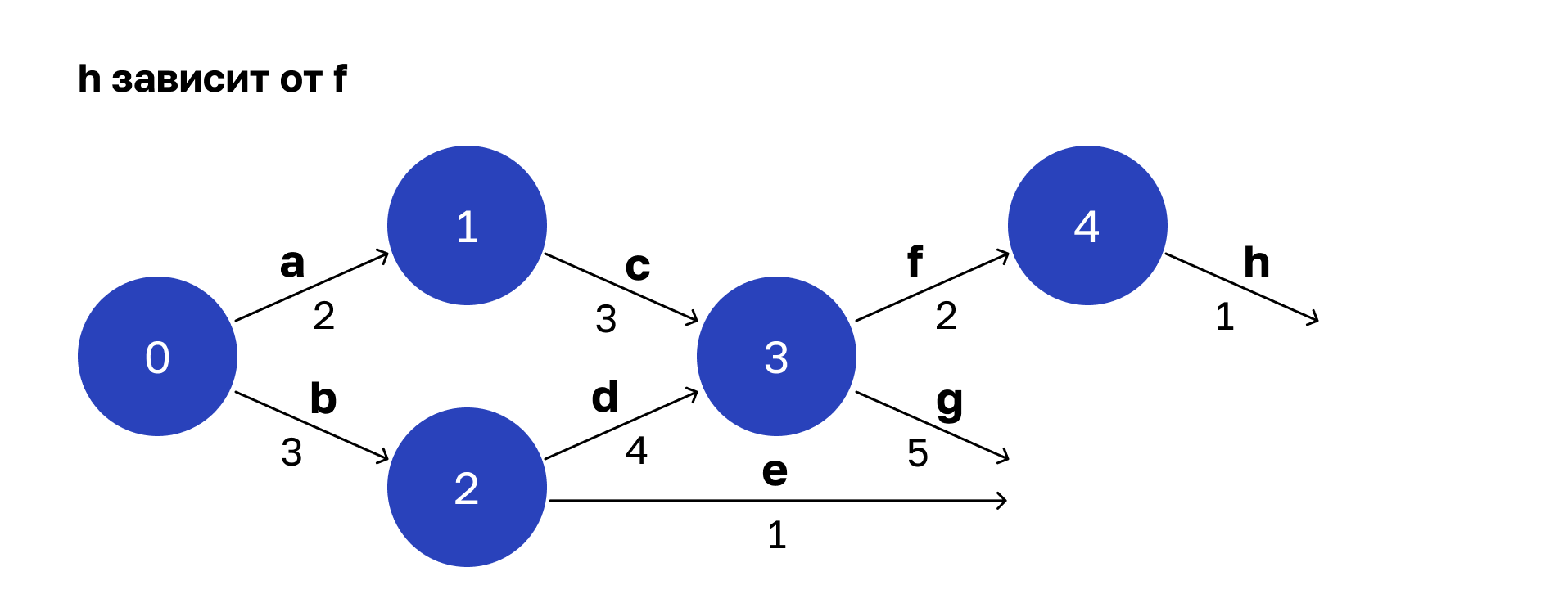
Операция h зависит от результатов выполнения операции f. Выполнению соответствует вершина 4.

И завершающий этап. 

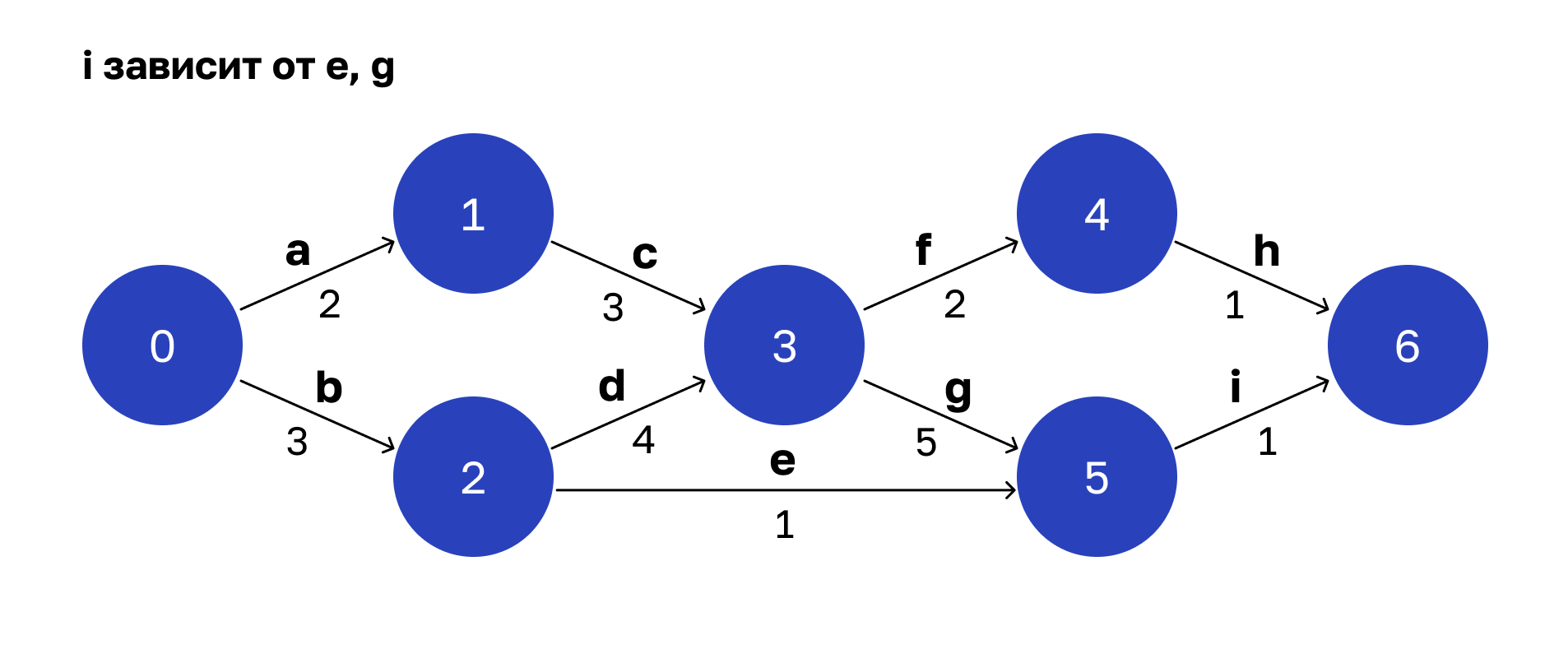
Операция i зависит от e и g. Финальное состояние системы — под номером 6. Это результат завершения параллельных операций h и i.

Таким образом, мы получили технологическую карту того, как собирается ответ на запрос. На ее основе можем приступать к оптимизации. В итоге получим хороший выигрыш во времени. Но можно отжать кое-что еще.

Оптимизируем операции

Как мы покажем дальше, достаточно оптимизировать только некоторые операции, а не все подряд. Найти те, которые стоит ускорять, поможет раннее и позднее расписание. 

Рассчитываем раннее расписание

Раннее время для каждой вершины — это самый ранний момент, когда может наступить конкретное состояние. Совокупность ранних времен назовем ранним расписанием.

Вот что у меня получилось:

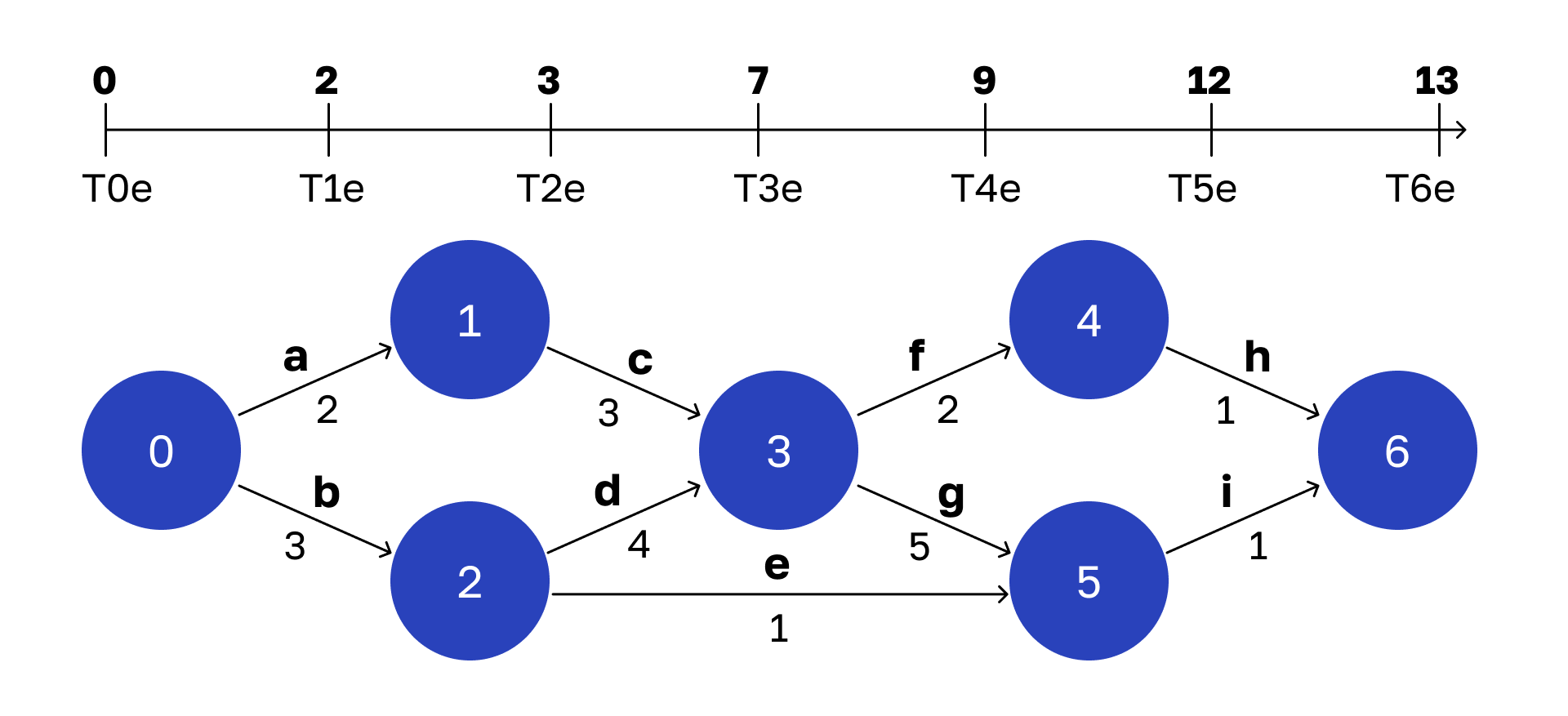
Давайте разберемся, как я это посчитал.

Начнем с простого. Ранним временем начальной вершины будет 0. Оно соответствует поступлению запроса на обработку. Тогда же система переходит в состояние 0, то есть: 

T0e = 0

Как вычислить раннее время вершины 1? Чтобы достичь состояния 1, мы должны завершить операцию a. Она занимает 2 единицы времени. Стартуем с нулевого момента, выполняем операцию a за 2 единицы времени и переходим в состояние 1. Следовательно:

T1e = 2

Аналогично вычисляется время следующей вершины:

T2e = 3

Теперь переходим к вершине 3. Чтобы попасть туда, нужно завершить операции c и d. Какое самое раннее время завершения операции c? 

Посчитаем:

T1e = 2
Время выполнения операции c = 3
Поэтому T3e не может быть меньше чем: 2 + 3 = 5 

Но еще же должна завершиться операция d, для нее аналогичное вычисление:

T2e = 3
Время выполнения операции d = 4
Получаем, что T3e не может быть меньше, чем: 3 + 4 = 7

В итоге у нас получилось два значения раннего времени вершины 3. Нам нужно выбрать то, которое больше. Потому что иначе рискуем не успеть завершить более медленную операцию, и тогда состояние 3 не наступит.

T3e = max (5, 7) = 7

Аналогично рассуждаем о вершине 4. Получаем следующее:

T3e = 7
Время выполнения операции f = 2
T4e = 9

Так же вычисляются ранние времена для всех оставшихся вершин.

В итоге получаем, что раннее время конечной вершины равно 13 единицам. Это тот минимум, до которого можно сократить время обработки запроса, если реорганизовать код класса согласно сетевой модели. Напомню, что стартовали мы с 22, а теперь это число можно уменьшить до 13. По-моему, выигрыш существенный.

Рассчитываем позднее расписание

Теперь займемся узкими местами в нашем процессе. Для этого в каждой вершине вычислим так называемое позднее время — самый поздний момент, когда из вершины могут стартовать операции, чтобы не изменить общее время всего процесса (13 единиц). Соответственно, совокупность поздних времен называется поздним расписанием.

Вот что у меня получилось.

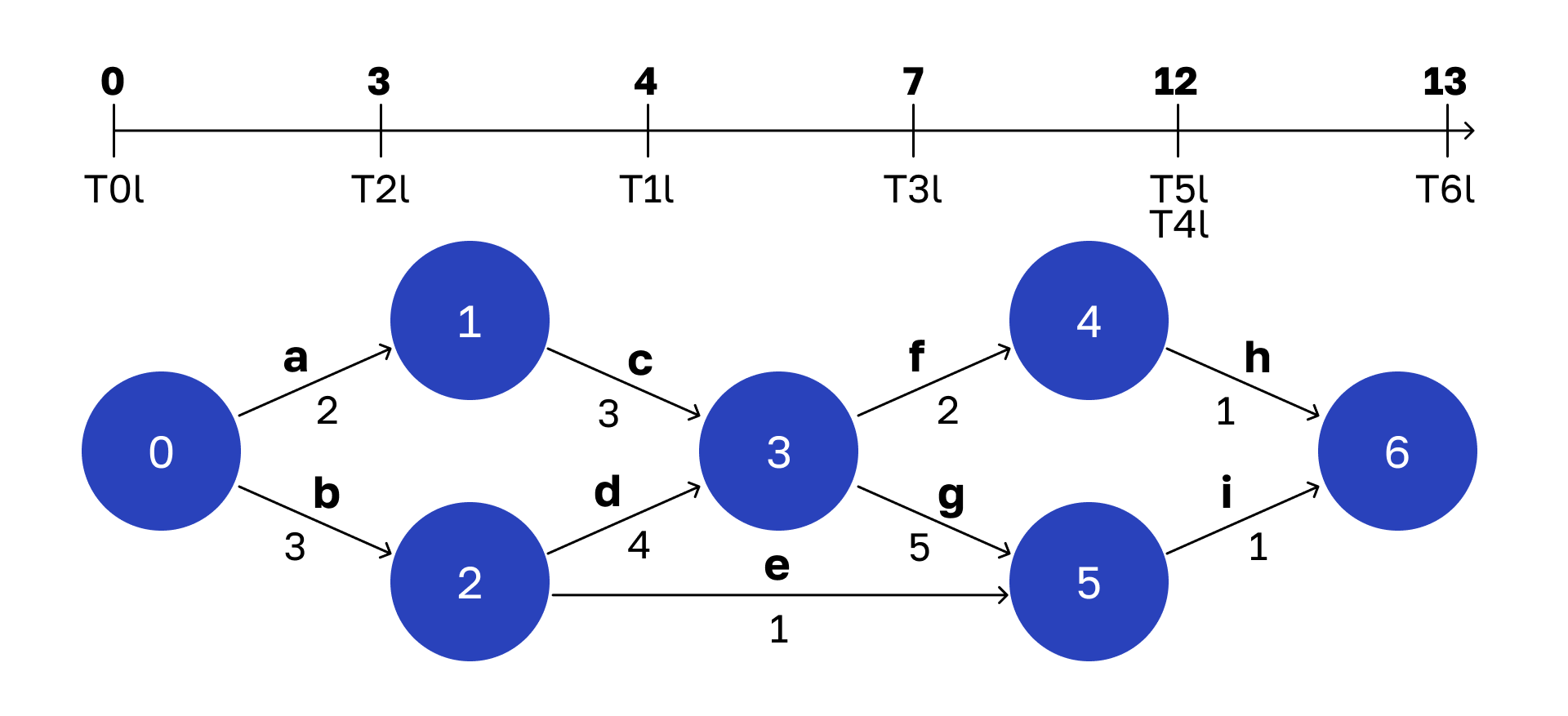
Логика расчета аналогичная, что и для раннего расписания, только мы обходим граф не от начала к концу, а наоборот — начинаем с вершины 6. 

На ней завершается весь процесс, поэтому ее раннее и позднее время совпадают. Итак:

T6l = 13

Посчитаем позднее время вершины 5. Из нее исходит одно ребро — операция i. На нее тратится 1 единица времени. Если будем выполнять эту операцию дольше, то опоздаем к вершине 6 вовремя, и тогда не уложимся в заданные 13 единиц. Поэтому позднее время будет рассчитываться следующим образом:

T5l = T6l - (время выполнения операции i) = 13 - 1 = 12

C вершиной 4 аналогичная ситуация:

T4l = 13 - 1 = 12

С вершиной 3 все интереснее. Из нее исходит 2 ребра. Какое самое позднее время начала выполнения операции f и g может быть?  Операция f занимает 2 единицы времени.  Чтобы не опоздать в вершину 4, мы от позднего времени вершины 4 должны отнять 2. Таким образом: 

T3l ≤  T4l - (время, которое занимает операция f) = 12 - 2 = 10

Еще есть операция g, которая занимает 5 единиц времени. При этом мы не должны задержать вершину 5. Следовательно:

T3l ≤ T5l - (время, которое занимает операция g) = 12 - 5 = 7

Из двух полученных чисел (10 и 7) мы должны выбрать минимальное, то есть 7.

T3l = min (10, 7) = 7

Для оставшихся вершин рассчитываем времена тем же самым способом. 

Строим критический путь

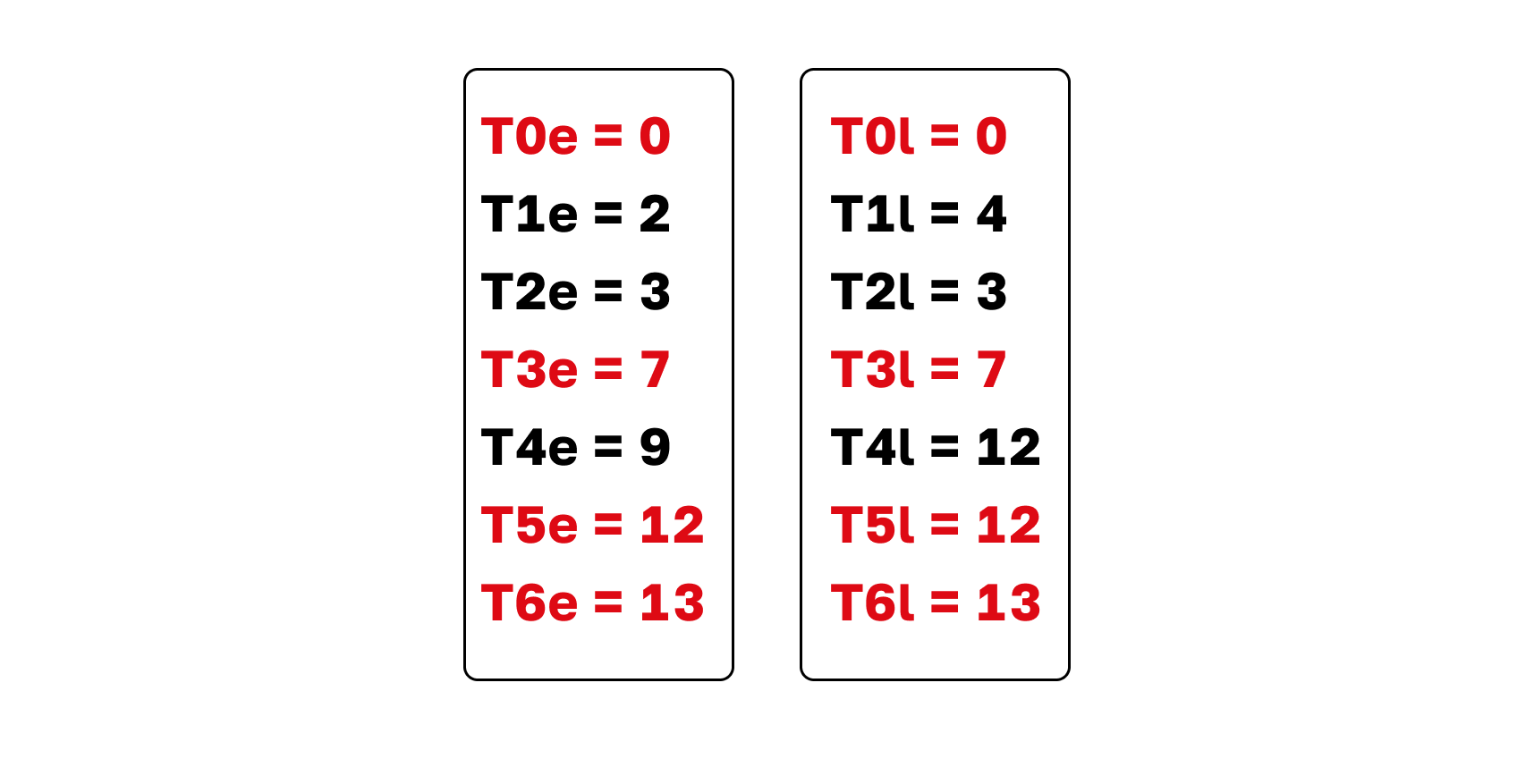
Теперь для каждой вершины мы имеем два параметра — раннее и позднее время. Если они различаются, значит, у нас есть резерв по срокам для исходящих операций. 

У вершин, выделенных красным, раннее время совпадает с поздним. У них нулевой резерв по таймингу. Путь, который проходит через них, называется критическим.

Если у какого-то этапа в таком пути изменится срок, это повлияет на время завершения всего процесса. Критических путей может быть несколько.

В нашем графе критический путь выглядит так.

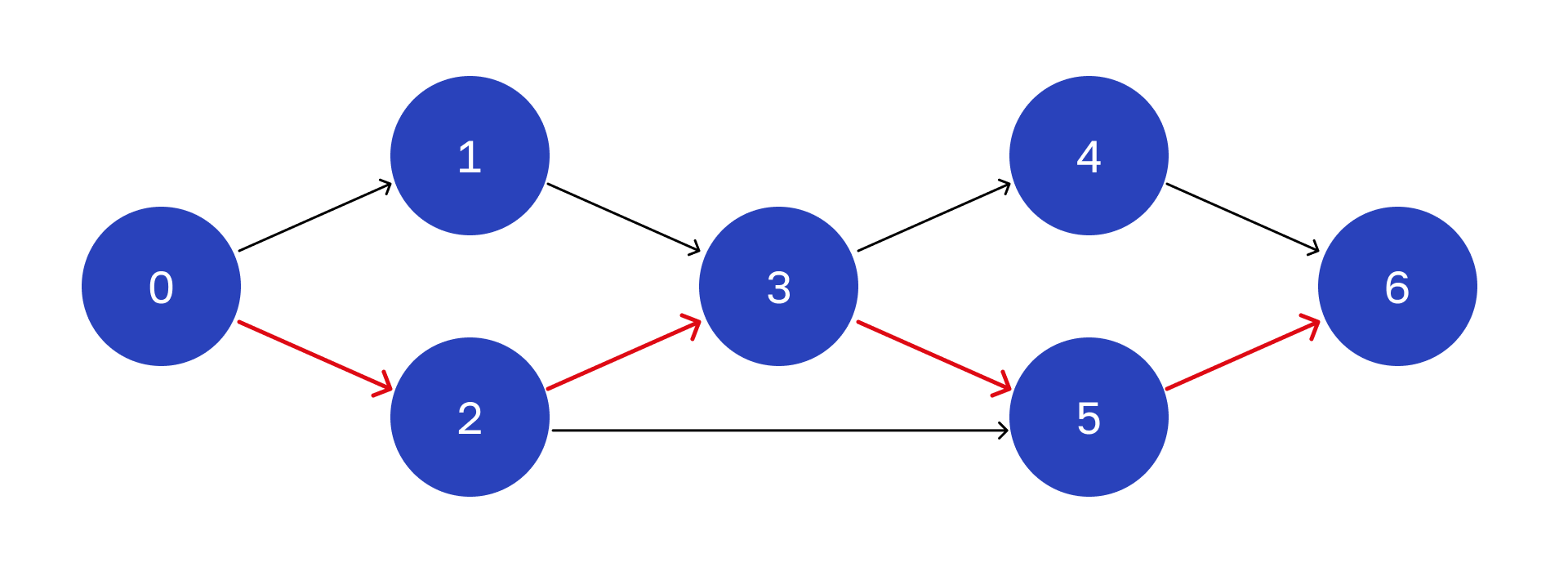
Что это нам дает? Нет смысла бороться за ускорение операций, которые не входят в критический путь. Это не приведет к уменьшению общего времени. 

А если удастся улучшить время хотя бы в одном месте критического пути, то общее время обработки снизится. Там и нужно ускорять операции.

Но после этого, возможно, критический путь изменится, и у вас возникнет другое узкое место. Понадобится провести новый анализ.

Каких результатов мы добились

У нас сервис, обрабатывающий запрос, включал 13 операций. Критический путь был единственным и содержал 6 операций.

Алгоритм сетевого планирования помог добиться следующего:

• Улучшилась читаемость кода. Считаю, здесь это основное, потому что читаемость кода — непреходящая ценность для каждого разработчика.

• Получили выигрыш во времени почти в 2 раза — и это только за счет распараллеливания.

• Нашли критические операции, которые стоит оптимизировать.

А главное, мы добились этих результатов просто с помощью реорганизации кода. 

Заключение

В бизнес-разработке сейчас царит увлечение готовыми решениями, фреймворками. Но иногда хороший профит может принести и обычная математика. 

Так что мой вам совет: изучайте простейшие алгоритмы — они реально могут помочь в работе.