Преамбула
Собственно, зачем. Когда-то мои поиски качественного описания симплекс-метода заняли уйму времени. Для того, чтобы прочие не страдали, я постараюсь изложить более полную информацию о решении задач данным способом. Кому-то, возможно, эта тема покажется далекой от IT, однако она полезней, чем подумают многие. Скажем даже больше, до наступления эры квантовых компьютеров оптимизация будет играть ключевую роль в работе настоящих программистов. Статья довольно тяжелая, но при надобности можно и потерпеть.
Постановка
Крайне важную нишу в методах оптимизации занимают задачи линейного программирования (ЛП). Они заключаются в минимизации (или максимизации) целевого линейного функционала на многомерном пространстве при наличии ограничений, заданных в виде линейных неравенств. Формально каноническая задача ЛП выглядит следующим образом:
Требуется найти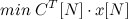 
при заданных ограничениях 
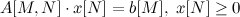. Для ясности: x — вектор переменных, C — вектор коэффициентов (C^T[N]*x[N] и задает линейный функционал). Матрица А является матрицей полного ранга, иначе говоря rang A[M, N] = min(M, N).
Приведем тривиальный пример. Допустим, мы ищем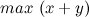 
при условиях: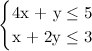 
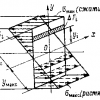
Для лучшего представления прикладываю график множества ограничений:
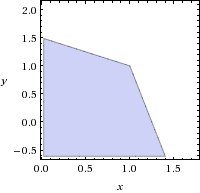
WolframAlpha утверждает, что максимум достигается в точке (1, 1). Попробуем решить сами и тем самым проверить. В нашем случае задача далека от канонической. Для начала заменим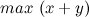 
на эквивалентное 
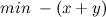. Но что же делать с неравенствами в ограничениях? Для таких случаев вводятся дополнительные переменные и… Voilà! Задача готова.
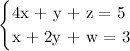
В случае, если ограничение в виде неравенства «больше или равно», вместо +z, очевидно, стоит вставить -z.
Здесь я добавил условия неотрицательности переменных. В этом примере они необязательны для существования максимума, но требуются для применения симплекс-метода. Если переменная x может принимать отрицательные значения, то её можно заменить на разность неотрицательных y и z.
Итак, теперь мы получили каноническую задачу, где
, 
, 
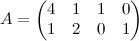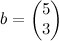
Поиск оптимального решения
Несколько определений и теорем.
- Оптимальным решением назовем такой вектор x, который соответствует
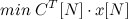. - Точка x называется крайней на выпуклом множестве S (КТ), если невозможно найти две такие точки из S, чтобы x располагалась на отрезке их соединяющем. Возвращаясь к нашей задаче, демонстрирую:
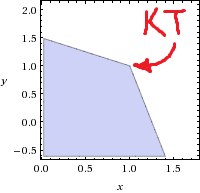
- Вектор x[N] называется опорным, если столбцы матрицы А, соответствующие положительным компонентам x, являются линейно-независимыми. Если количество этих положительных компонент меньше ранга А, то вектор называется вырожденным.
- Удивительный факт, но легко доказывается. Опорный вектор — это тоже самое, что и крайняя точка.
- Если существует оптимальное решение, то оно достигается в опорном векторе и, соответственно, в КТ (что и подтвердил всемогущий Wolfram).
Казалось бы, ну теперь все просто. Можем перебрать все крайние точки (в нашей задаче, если не учитывать неотрицательность переменных, она вообще единственная) и сравнить значения целевых функций, после чего отобрать минимальное. Увы, все будет посложней. Количество опорных векторов может достигать аж, внимание, C(m, n), что при довольно большом n и m близком к n/2 может достигать колоссальных размеров.
И здесь нам на помощь приходит ранее упомянутый метод.
Симплекс-метод
Основная идея симплекс-метода заключается в переходе от одного опорного вектора к другому таким образом, чтобы значение целевой функции не возрастало. То есть, будем двигаться так, чтобы на каждом k-м шаге мы имели:
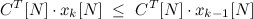
Основной этап
Здесь, вероятно, придется поднапрячься. Допустим, мы построили начальный опорный вектор x. Воспользуемся некоторыми из условий оптимальности. Для того, чтобы x был оптимальным решением задачи ЛП необходимо и достаточно, чтобы существовал y, такой что:
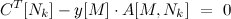
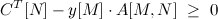
Есть еще условия, но вдаваться в подробности и выписывать доказательство сей теоремы я не стану, дабы не расширять и без того немалую статью — это хорошая тема для отдельного поста.
Появившееся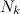 
— это как раз-таки положительные компоненты вектора x на k-м шаге, базисные элементы. Обозначим за 
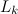те компоненты x, что не входят в 
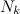. Так как определитель матрицы 
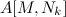не равен нулю (из определения опорного вектора), то можем разрешить уравнение относительно y[M].
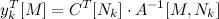
Теперь, если подставим y[M] во второе уравнение, то относительно базисных компонент получим равенства нулю (как в первом), а в строчках, соответствующих небазисным:
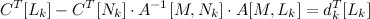
Так видно, что если вместо L будет N, то получим тождественное равенство нулю. Если каждая компонента вектора d неотрицательна, то условие выполнено — мы нашли оптимальное решение. Иначе, следует искать новый опорный вектор, да еще и таким образом, чтобы целевая функция не уменьшалась.
Допустим, мы нашли такой номер j, что компонента d[j]<0. Строим вектор u[N] следующим образом:
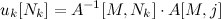
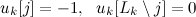
С его помощью мы перейдем к новому опорному вектору. Рассмотрим вектор
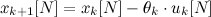, где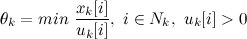 
Если старый опорный вектор не вырожден, то несложно проверить, что
1. Новый опорный вектор попадает в множество ограничений (содержит только неотрицательные компоненты, а также удовлетворяет СЛАУ Ax=b).
2. Новое значение целевой функции не превосходит старого.
Уменьшение целевой функции напрямую зависит от коэффициента θ, поэтому его и выбирают как наибольшее из возможных, а именно вышеуказанным образом.
Внимание. Если вектор u[N] <= 0, то θ можно устремить к бесконечности, что приведет к тому, что минимальное значение целевой функции будет достигаться на -бесконечности. Следовательно, функция не ограничена снизу на допустимом множестве, алгоритм заканчивается.
Но если опорный вектор вырожден (напомню, в этом случае количество нулевых компонент вектора x превышает число небазисных столбцов), действуют следующим образом. Если в векторе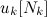 
среди компонент, соответствующих нулевым компонентам x не нашлось положительных, находим θ по предыдущей формуле. В противном случае, так искать нельзя. И тогда пытаются поменять базис старого опорного вектора: берется столбец из A, соответствующий базисной нулевой компоненте x и меняется на столбец, соответствующий какой-нибудь небазисной компоненте. Если добились того, что новая система векторов линейна-независима, возвращаемся к началу алгоритма, иначе проводим замену снова.
Замечание
Искать обратную матрицу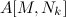 
— задача довольно трудоемкая. Но мы знаем, что 
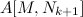отличается от 
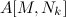лишь одним столбцом, стоящем на i-м месте. Поэтому, новую обратную можем искать из следующего соотношения:
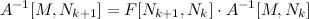, где матрица F отличается от E лишь одним i-м столбцом:
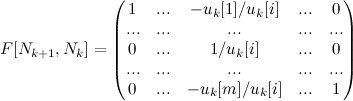
Кстати, это соотношение доказывает существование обратной новой матрицы A, что говорит о том, что новый x является опорным вектором.
Итак, прогоним алгоритм еще раз.
Основной этап:
1. Находим вектор d. Если он неотрицателен, то оптимальное решение найдено — выходим.
2. Строим вектор u. Если все его компоненты не превосходят нуля — функция не ограничена снизу — выходим.
3. Если опорный вектор невырожденный или же среди компонент вектора u, соответствующих базисным нулевым компонентам x не нашлось положительной, то новый опорный вектор ищем по формуле x = x — θu. Иначе, производим смену базиса до тех пор, пока новая система из столбцов A не будет ЛНЗ.
4. Вычисляем обратную матрицу А и возвращаемся к шагу 1.
Построение начального опорного вектора
Для построения НОВ рассмотрим вспомогательную задачу:
, 
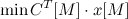
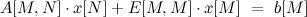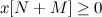
То есть, мы добавляем m новых переменных. Без ограничения общности можем считать b[M] >= 0. Иначе, домножаем нужную строчку на -1. Тогда для вспомогательной задачи на роль начального вектора, очевидно, можно выбрать следующий: x[N]=0, x[M]=b[M].
В примере это будет выглядеть так:
, 
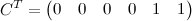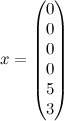
Если решением вспомогательной задачи является такой вектор x, что ∃j∈M: x[j]>0, очевидно, что исходная задача не имеет допустимых точек. Иначе, если он не является вырожденным, его можно использовать в качестве опорного в исходной задаче. В противном случае может оказаться так, что некоторые базисные элементы соответствуют не матрице A, а единичной E. Тогда следует произвести замену базисных столбцов, соответствующих E на столбцы из A.
Заключение
Решать заданный пример симплекс-методом, конечно же, все равно что слонобоем по мухам стрелять. Достаточно домножить первую строку на 1/7 и вычесть вторую, домноженную на -3/7. И сразу станет ясно, где достигается максимум. Однако, этот метод предназначен для примеров, где не так все очевидно.
Подытожив, хочу заметить, что симплекс-метод может также быть полезен, если ограничения нелинейны. В этом случае с его помощью можно решать этапные задачи в методе Зойтендейка, а также в методе условного градиента. Спасибо за внимание.
Список литературы:
Петухов Л.В., Серегин Г.А. «Учебное пособие»; Ленинградский гос. техн. ун-т 1991
Пшеничный Б.Н., Данилин Ю.М. «Численные методы в экстремальных задачах»; Наука, 1975
Автор: The_Freeman
