Сглаживание цифровых сигналов

Введение

Математические модели цифровых сигналов — вектора и матрицы, элементами которых являются числа. Числа могут быть двоичными (бинарный сигнал), десятичными («обычный» сигнал) и так далее. Любой звук, любое изображение и видео могут быть преобразованы в цифровой сигнал¹: звук — в вектор, изображение — в матрицу, а видео — в последовательный набор матриц. Поэтому цифровой сигнал — это, можно сказать, универсальный объект для представления информации.

Задача сглаживания — это, по сути, задача фильтрации сигнала от высокочастотных составляющих (попросту говоря, от шума). Поэтому для разработанного алгоритма сглаживания в первую очередь необходимо определить как сильно ослабляются разные частотные составляющие. Другими словами, необходимо построить амплитудно-частотную характеристику соответствующего фильтра, иначе велика вероятность «нарваться» на артефакты.

Например, при попытке сгладить звуковой сигнал по двум соседним отсчётам весьма вероятно, что в голову придёт формула вроде

       v[i] = (s[i+1] + s[i] + s[i-1])/3. 

Казалось бы, обычное усреднение и мощность шума должна уменьшиться… Да, уровень шума после фильтрации будет меньше, но где гарантия того, что в вышеприведённом алгоритме справедливо следующее утверждение: чем выше частота шума, тем в большей степени он будет ослаблен? Ведь, по логике, немонотонная характеристика (то — убывающая, то — возрастающая) ничем не оправдана… Как построить зависимость ослабления от частоты для конкретного алгоритма? Как подобрать коэффициенты сглаживающего фильтра (в вышеприведённом алгоритме коэффициенты равны по 1/3)? А может быть взять не три слагаемых, а пять? Как найти свой (то есть для конкретной задачи) оптимум?

На эти и некоторые другие вопросы я постараюсь ответить так, чтобы обычный программист смог обосновать свой алгоритм, — надеюсь, не только алгоритм на тему «Сглаживание», так как идеи будут излагаться весьма общие, заставляющие думать самому…

Сигналы

В этом параграфе под сигналом понимается вектор, то есть массив из определённого количества чисел. Например, вектор из четырёх элементов s = (2,5; 5; 0; -5).

Для простоты будут рассматриваться только десятичные вещественные числа.
Одним из наиболее распространённых и понятных сигналов является оцифрованный звук. Размер сигнала зависит от длительности звука и от частоты, с которой делают выборки (от частоты дискретизации). Элементы-числа сигнала зависят от текущей амплитуды звука, измеряемой устройством выборки и хранения.

Как уже было сказано, один из самых простых способов сглаживания, это
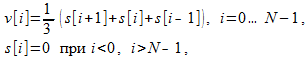(1)
где s — исходный сигнал, v — сглаженный сигнал, N — размер сигнала.

Способ (1) основан на сглаживающем свойстве суммирования, ведь каждому ясно, что средняя величина, вычисляемая как сумма многих случайных чисел, с ростом количества суммируемых чисел становится всё менее и менее похожей на случайную величину ², которая, попросту говоря, и есть шум ³.

Но на чём основан выбор коэффициентов в уравнении (1)? На том, что так вычисляется среднее? Вроде бы да, но… А если взять не три слагаемых, а шестнадцать? А тридцать два?.. Почему всё более отстоящие от центрального элемента s[i] отсчёты должны браться с одинаковым весом? Ведь может оказаться так, что связь между отсчётами будет постепенно ослабевать с ростом расстояния ⁴ между ними?
Если рассмотреть пример произношения слова «арбуз» десять раз подряд и попытаться отследить связь между отсчётами записанного сигнала, то можно обнаружить ослабление зависимости между всё более отстоящими друг от друга отсчётами. Естественно, что если рассмотреть «большие расстояния», то звуки будут повторяться за счёт повтора одного и того же слова и зависимость будет нарастать и снова спадать, и так далее. Но, как правило, «большие расстояния» при сглаживании не рассматривают, так как шумы проявляются в окрестности отдельных звуков, а не слов, фраз и предложений. Шум, действующий на уровне слов или даже фраз — это явно искусственный (звуковые эффекты) или экзотический естественный (эхо). Это — уже «неслучайный» шум, требующий отдельного исследования. Здесь рассматривается «чистый» шум, который, говоря простым языком, раздражающе шумит и нисколько не похож на какой-либо полезный сигнал.

На основании простых рассуждений становится очевидным, что количество слагаемых в (1) (порядок фильтра) должно зависеть от того, насколько сильно зависят друг от друга соседние отсчёты. Например, нет смысла брать фильтр тридцатого порядка, если наблюдается зависимость только лишь десяти отсчётов, следующих друг за другом. На самом деле даже не то, что «нет смысла», а — нельзя, так как если отсчёты практически не связаны, то начнётся чрезмерное сглаживание полезного сигнала («съедение» слогов). Но и фильтр третьего порядка здесь не будет оптимальным по степени использования информации о полезном сигнале, так как, как уже было сказано, наблюдается зависимость порядка десяти соседних отсчётов. Поэтому можно «попытать счастья» с помощью фильтра девятого порядка, естественно, увеличив нагрузку на процессор-вычислитель. Здесь уже требуется определить, скорее всего экспериментально, а стоит ли данная игра свеч?..

Как оценить насколько сильно связаны соседние отсчёты? Вычислить автокорреляционную функцию (АКФ). Желающим можно предложить провести эксперимент по записи разных слов, фраз, повторов фраз и последующему построению АКФ (благо, например, программа Matlab позволяет это сделать, особо не задумываясь над кодом и формулами).

А как выбрать коэффициенты фильтра? В данном случае удобно рассмотреть реакцию фильтра на единичное воздействие, то есть на сигнал вида 1, 0, 0,….

Например, фильтр (1) даст следующий отклик (импульсную характеристику)

        1/3, 1/3, 0, 0, ... ,

откуда мы можем сделать вывод, что после сглаживания длительность сигнала стала равна двум элементам. А если взять фильтр из пяти элементов?.. Правильно, длительность увеличится в четыре раза. Насколько это полезно, определяется конкретной ситуацией (задачей).

Если частота дискретизации сигнала выбрана достаточно большой, то есть, например, восемь соседних отсчётов содержат практически одну и ту же информацию, то имеет смысл использовать фильтр восьмого порядка для большего подавления шума (считается, что даже два соседних отсчёта шума не зависят друг от друга).

Если сигнал звуковой, то он достаточно хорошо описывается набором гармонических сигналов ⁵ («синусоид») и степень ослабления конкретной синусоиды зависит от её частоты. Опять же, при грамотном выборе сглаживающего фильтра никакая из полезных синусоид не должна пропадать полностью, то есть амплитудно-частотная характеристика фильтра в рабочем диапазоне частот не должна содержать глубоких провалов.

Посмотрим на фильтр (1) с другой стороны — с частотной.

Пропустим через рассматриваемый фильтр один однотональный сигнал определённой частоты, естественно, не выходя за пределы теоремы отсчётов. Пусть шаг дискретизации по времени T_d равен единице, то есть отсчёты идут с шагом одна секунда. Возьмём сигнал с частотой f = 1/(3T_d) = 1/3 Гц, то есть

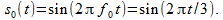
Ограничимся двумя периодами

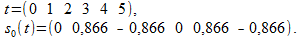
Отклик фильтра (1) будет равен

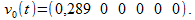
Как ни странно, получили почти ноль… Получается, можно потерять некоторые составляющие полезного сигнала.

Проверим несколько более высокочастотный сигнал (f₁ = 2/5 Гц), то есть

Как видим, форму сигнала не потеряли. В чём же дело?..

Дело в том, что амплитудно-частотная характеристика фильтра (1) не является монотонной в рабочей полосе частот (в полосе от нуля до половины частоты дискретизации) и имеет один нуль на частоте, в три раза меньшей частоты дискретизации. Как это показать?

Попросту говоря, чтобы определить частотную характеристику фильтра, необходимо найти отношение спектра на выходе фильтра к спектру на входе.

Обозначим спектр сигнала s[i] на входе как S( f ), тогда спектр задержанного на один такт T_d сигнала s[i-1] выразится через спектр исходного сигнала как
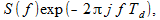(2)
где j — мнимая единица.

Спектр опережённого сигнала s[i+1] выразится как
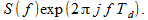(3)

Что означает мнимая единица? И как можно обосновать (2) и (3)?
Если записать известные [1, 2] ряды для синуса, косинуса и экспоненты
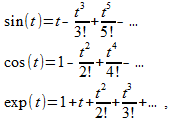(4)
то подобрав число j, такое, что j² = –1, можно последний ряд выразить через два первых
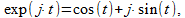(5)
что означает то, что любое комплексное число можно записать через экспоненту с мнимым показателем. Модуль числа (5) равен единице (корень квадратный из суммы квадратов мнимой и реальной частей), поэтому для записи любого комплексного числа в форме (5) его необходимо разделить и умножить на свой модуль
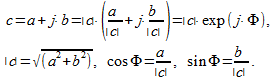(6)

Из (5) и (6) следует, что если в показателе экспоненты можно выделить мнимую единицу, умноженную на некоторое действительное число, то это число является аргументом комплексного числа.

В данном случае рассматриваются сигналы, поэтому модулю комплексного числа соответствует амплитуда гармонического сигнала, а аргументу — фаза. Если, например, взять сигнал вида
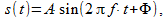(7)
то можно выделить амплитуду A и фазу Ф. Множитель 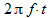— это также фаза, и в некоторых случаях её выносят за скобки. Например, при прохождении сигнала (7) через некоторый фильтр важно знать разность фаз сигналов на входе и выходе, которую вносит фильтр на заданной частоте f.

Если сигнал (7) задержать на величину t₀, то получится тот же самый сигнал, но сдвинутый по фазе на постоянную величину
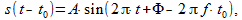(8)
то есть при задержке произвольного сигнала все его частотные составляющие сдвигаются по фазе на величину, зависящую от текущей частоты и величины задержки. Этим можно объяснить формулы (2) и (3). Поэтому при анализе какого-либо алгоритма важна и фазо-частотная характеристика, которая показывает на какое время задерживает фильтр (алгоритм) каждую частотную составляющую входного сигнала. Низкие частоты и высокие в общем случае будут иметь разную задержку в фильтре.

Из (1), (2) и (3) следует, что частотная характеристика фильтра (передаточная функция) будет иметь вид
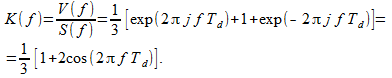(9)

Так как спектр выходного сигнала линейно выражается через спектр входного, то при выводе (9) спектр входного сигнала успешно сокращается. Далее замечаем, что частотная характеристика фильтра (1) — действительная, то есть данный фильтр не вносит фазовых искажений ⁶. Этого мы достигли (скорее всего, неосознанно) за счёт симметричности формулы (1): каждый отсчёт на выходе фильтра равен сумме текущего и двух соседних отсчётов.

Физически такой алгоритм реализуем только при наличии запоминающих устройств, так как в нём используются опережающие отсчёты (для вычисления отсчёта s[i] требуется отсчёт s[i+1]). В настоящее время это не является большой проблемой и, как правило, используют симметричные алгоритмы. Если фазовые искажения окажутся полезными, то — пожалуйста, главное осознанно применять какой-либо алгоритм и смотреть на него с разных сторон: с частотной и временной.

Построить график зависимости (9) от частоты не составляет труда, правда для упрощения вводят нормированную частоту f₀  = f T_d , полезный диапазон изменения которой [0…0,5]. Составляющие сигнала с частотами выше половины частоты дискретизации по теореме отсчётов должны отсутствовать (перед оцифровкой сигнал пропускают через соответствующие фильтры нижних частот). Частота дискретизации показывает количество выдаваемых цифровым устройством отсчётов в секунду. Если, например, один такт T_d равен одной миллисекунде, то за одну секунду должна быть выдана тысяча отсчётов.

Анализируя (9) можно заметить, что на некотором промежутке коэффициент передачи меньше нуля, а амплитуда — это по определению положительная величина… Выход из ситуации — построить модуль передаточной функции, убрав знак минус в фазовую характеристику, которая, всё-таки, не является константой (нулём). Если взять число «минус единица», то его по формуле (5) можно представить как
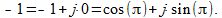(10)
то есть комплексным числом, имеющим модуль «единица» и фазу «180 градусов» («пи»).

Таким образом, трёхточечный симметричный алгоритм (1) для некоторых «высоких» частот вносит сдвиг по фазе на 180 градусов, то есть попросту инвертирует входной сигнал. Этот эффект можно заметить, анализируя рассмотренный выше отклик на нормированную частоту 2/5 Гц.

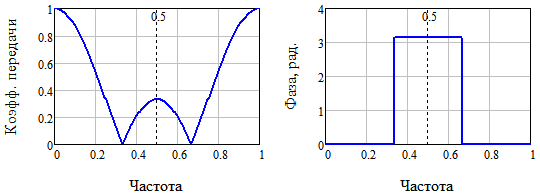
Рис. 1. Амплитудно-частотная и фазо-частотная характеристики трёхточечного симметричного алгоритма сглаживания (1)

Из рис. 1 сразу следует, что сигнал с частотой 1/3 будет данным алгоритмом подавлен, а сигналы, имеющие частоту выше 1/3 будут инвертированы. Таким образом, полезный рабочий диапазон частот можно смело сократить с [0…0,5] до [0…1/3]. Если нас не устраивает быстрое спадание коэффициента передачи, придётся определять другой алгоритм, имеющий более прямоугольную амплитудно-частотную характеристику и при этом — ещё неизвестно какую фазовую…
Если теперь записать алгоритм (1) в более общем виде
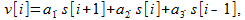(11)

то, основываясь на знании частотной характеристики, можно попытаться подобрать коэффициенты, ставя целью монотонность амплитудно-частотной характеристики (то есть невозрастание модуля в пределах нормированных частот от 0 до 0,5). Для этого как минимум необходимо отсутствие нулей в интервале частот (0…0,5).
Так как у нас нет оснований выделять запаздывающий отсчёт s[i–1] по отношению к опережающему s[i+1], то приравняем коэффициенты a₁ и a₃. После запишем коэффициент передачи
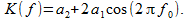(12)

Попытаемся переместить первый нуль на частоту f₀ = 0,5. Для этого должно выполняться равенство a₂ = 2a₁ , то есть вес у боковых отсчётов должен быть в два раза меньше веса центрального. Тогда более оптимальный алгоритм будет выглядеть так
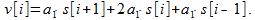(13)

Как в (13) выбрать единственный коэффициент a₁?
Теперь можно взглянуть на алгоритм (13) с временной точки зрения. Импульсная характеристика будет иметь вид
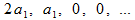(14)

Если мы не хотим изменять энергетику входного сигнала, то коэффициенты следует выбрать так, чтобы сумма квадратов всех отсчётов импульсной характеристики была равна единице. Входной сигнал в виде одного единичного отсчёта, определяющий импульсную характеристику, этому удовлетворяет, а так как любой сигнал можно естественным образом разложить в ряд по единичным отсчётам, то энергия на выходе будет равна энергии на входе.

Таким образом, уравнение

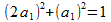
даёт корень
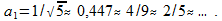(15)

Выбирая разные рациональные приближения иррационального числа (15), можно получать немного разные алгоритмы, отличающиеся в степени потерь энергии сигнала на выходе. Например, выбирая a₁ = 2/5, получим энергию на выходе в 0,8 раз меньше. При a₁ = 4/9 коэффициент будет равен 80/81, что гораздо ближе к единице.

Рациональные аппроксимации полезны при целочисленных реализациях алгоритмов.
Наконец, для алгоритма
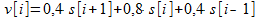(16)
можно построить (рис. 2) частотные характеристики: амплитудную и фазовую.

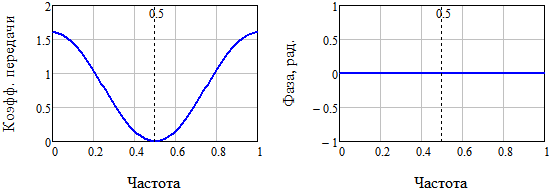
Рис. 2. Амплитудно-частотная и фазо-частотная характеристики трёхточечного симметричного алгоритма сглаживания (16)

Анализ рис. 2 показывает, что фазовые искажения исчезли, а амплитудные стали монотонными в рабочей полосе частот [0…0,5]. То есть в каком-то смысле мы выжали из трёхточечного фильтра «всё». Коэффициент передачи для некоторых частот больше единицы, так как мы хотели сохранить энергетику входного сигнала (у нас получился сглаживающий фильтр с дополнительным усилителем).
Теперь становится очевидно, что простое усреднение далеко не всегда является оптимальным, особенно когда усредняемых отсчётов много.

Изображения

Что касается изображений, то здесь в какой-то мере всё то же самое, что и для сигналов: амплитудные и фазовые искажения, импульсные характеристики, энергия сигнала, — основное отличие заключается в том, что используются матрицы вместо векторов. Также следует учесть, что для изображений нет координаты времени, а есть координата пространства, поэтому есть пространственные частоты дискретизации. Данное отличие скорее формальное, так как на математику алгоритмов оно не влияет вообще.

Рассмотрим теперь «самый простой» алгоритм сглаживания изображения по соседним точкам (рис. 3)
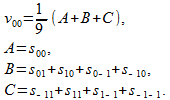(17)

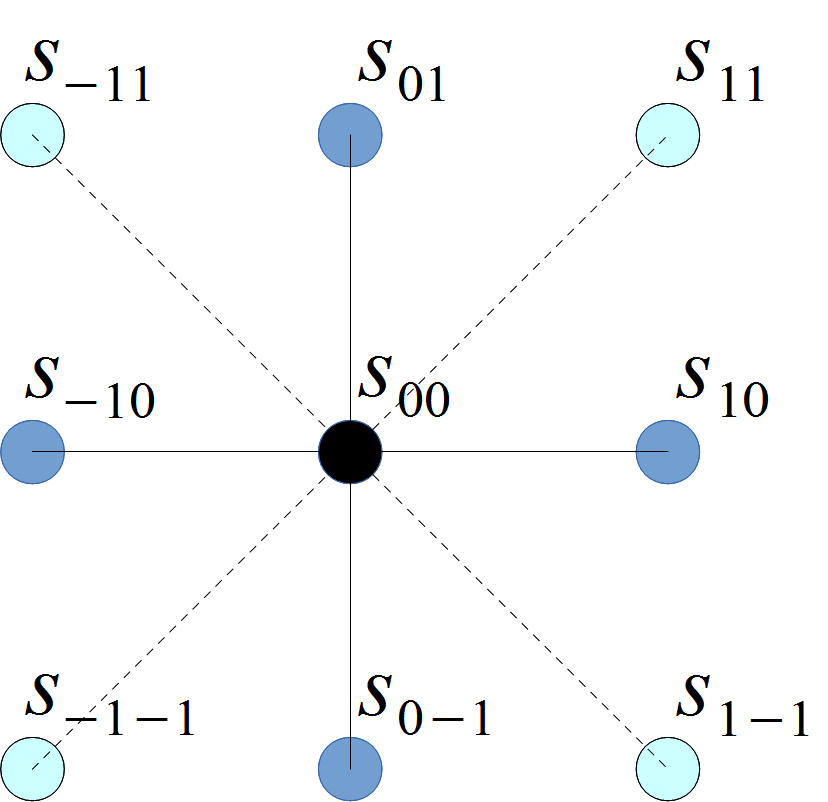
Рис. 3. Схема сглаживания изображения по соседним точкам

В формуле (17) специально выделены три слагаемых A, B и C, так как четыре соответствующих внутренних слагаемых у B и C имеют свои расстояния от центрального отсчёта s₀₀. Здесь естественно предположить, что максимальный вес будет у слагаемого A, затем в порядке убывания — у B и C.

Для изображений спектр и коэффициент передачи будут двумерными, то есть будут зависеть от двух частот: первая частота — по горизонтали, вторая — по вертикали (здесь всё условно, для определённости).
Фильтр (17) имеет следующий коэффициент передачи
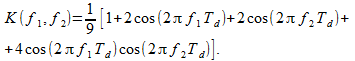(18)

Если взять, например, около тридцати дискретных частот и построить (рис. 4) контурный график модуля частотной характеристики (18), то можно увидеть искажения, аналогичные искажениям на рис. 1. Левому нижнему углу соответствуют самые низкие частоты. Наблюдается провал частотной характеристики на частотах, составляющих 1/3 от частоты дискретизации (частоты дискретизации в данном случае равны 64 по обеим координатам).

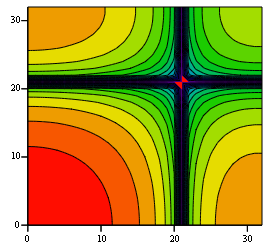
Рис. 4. Амплитудно-частотная характеристика девятиточечного симметричного алгоритма сглаживания (17)

Перетасовывая коэффициенты для отсчётов на рис. 3, можно получить следующий алгоритм сглаживания
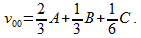(19)

Причём если единичное воздействие поместить в центре изображения, то отклик фильтра (19) будет иметь вид
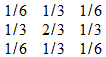(20)

По сути, (20) является импульсной характеристикой фильтра (это девять главных отсчётов, так как остальные равны нулю). Энергия импульсной характеристики (сумма квадратов элементов) равна единице. Частотная характеристика фильтра (19) имеет вид, показанный на рис. 5.

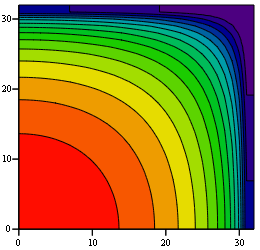
Рис. 5. Амплитудно-частотная характеристика девятиточечного симметричного алгоритма сглаживания (19)

Опять мы видим (сравни рис. 4 и рис. 5) улучшение алгоритма обычного усреднения.

Резюме

При разработке алгоритмов обработки цифровых сигналов (сглаживания и не только) не следует доверять интуитивным алгоритмам вроде простого усреднения.
Более общим подходом является техника весового суммирования (рассматривались только линейные алгоритмы, когда отсчёты только лишь умножаются на константы, а результаты — складываются).
Весовое суммирование, когда более отдалённым от центрального элемента отсчётам ставятся меньшие веса, оправдано как статистически (естественная природа ослабления зависимости с ростом расстояния), так и функционально (возможно строго математически подобрать коэффициенты, обеспечив монотонность амплитудно-частотной характеристики).
Большую роль играют амплитудно-частотные характеристики фильтров, которые определяются коэффициентами весового суммирования. Они позволяют доказать, что заданный фильтр пропускает определённый диапазон частот и заграждает другой. Причём можно определить неравномерность в полосе пропускания, в полосе заграждения и так далее. Чем больше порядок фильтра, тем больше степеней свободы и тем лучше можно подобрать форму амплитудно-частотной характеристики.
Важную роль играют и фазо-частотные характеристики, которые, в основном, определяются степенью симметричности алгоритма. Алгоритмы реального времени, когда в момент прихода первого отсчёта появляется отсчёт на выходе фильтра, не могут обеспечить равномерную фазовую характеристику (константу, чаще всего «нуль»), так как они не могут быть симметричными. Такие алгоритмы вносят задержку во входной сигнал: например, сглаженное изображение может в целом сместиться по обеим координатам. Если изображение сложное (то есть имеет много частотных составляющих), то фазовые искажения его могут заметно исказить, а не просто сместить по координатам, что приближённо справедливо для простых изображений.
Также следует обратить внимание на импульсную характеристику фильтра, соответствующего некоторому алгоритму. Это позволяет взглянуть на работу фильтра напрямую, то есть в масштабе времени для сигнала (или пространственных координат для изображения).
И, наконец, необходим энергетический анализ алгоритма, позволяющий определить потери сигнала на выходе соответствующего фильтра. Данный анализ удобно провести в терминах импульсной характеристики.

Сноски

1. Всегда с потерями, так как частота работы и разрядность цифровых устройств ограничены
2. Стабилизирующее свойство средней величины справедливо при неизменности характеристик генератора случайных чисел, то есть в идеале генератор должен выдавать случайную величину с заданным законом распределения
3. Если, конечно, наблюдаемый шум — это не зашифрованный полезный сигнал, который становится случайным для тех, кто не имеет ключа…
4. Для звукового сигнала расстояние между отсчётами — это некоторый промежуток времени
5. Можно считать, что любой сигнал можно представить в виде суммы синусоид кратных частот, но звуковой по природе обязан «хорошо» раскладываться в ряд по частотам
6. Упрощённо можно сказать и так, подробности смотри ниже

Источники

1. Тригонометрические функции [Электронный ресурс], режим доступа: свободный, ru.wikipedia.org/wiki/%D2%F0%E8%E3%EE%ED%EE%EC%E5%F2%F0%E8%F7%E5%F1%EA%E8%E5_%F4%F3%ED%EA%F6%E8%E8
2. Экспонента [Электронный ресурс], режим доступа: свободный, ru.wikipedia.org/wiki/%DD%EA%F1%EF%EE%ED%E5%ED%F2%E0

Автор: sci_nov

Источник