Введение
При разработке систем распознавания образов часто возникают проблемы при оценке параметров, которые используются в качестве входного вектора. В данной статье я опишу подход, который можно применять при анализе векторов обучающей выборки, с целью обнаружения зависимостей между параметрами, а также сокращения размерности, что позволит в свою очередь сократить затрачиваемые вычислительные ресурсы при анализе данных и повысить репрезентативность обучающей выборки.
Целью данной работы является определение факторов входного вектора критериев обучающей выборки, предназначенных для решения данной задачи.
Проведение анализа
Входные вектора для анализа представляют собой вектор яркостей пикселей на изображении. Будут проанализрованы изображения размером 30 х 30, 50 х 50 и 70 х 70. Соотвественно, длина векторов составляет 900, 2500, 4900 параметров. Часть выборки представлена на этом рисунке
Более подробно об алгоритме факторного анализа можно почитать здесь. В общем виде модель выглядит следующим образом.
Задачу факторного анализа можно сформулировать следующим образом: определить минимальное число k таких факторов F1,…,Fk после учета которых исходная корреляционная матрица “исчерпается”, внедиагональные элементы ее станут близкими к нулю. Другими словами, это значит, что после учета k факторов все остаточные корреляции между исходными признаками должны стать незначимыми.
В основе модели метода главных компонент для выражения исходных признаков через факторы здесь лежит предположение о том, что число факторов равно числу исходных признаков (k=m), а характерные факторы вообще отсутствуют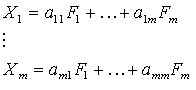 
. Уравнения определяют здесь систему преобразования одних параметров в другие. Поскольку число факторов равно числу исходных параметров, задача искомого преобразования решается однозначно, т.е. факторные нагрузки определяются в этом методе однозначно.
Каждая из переменных Fj называется здесь i-й главной компонентой. Метод главных компонент состоит в построении факторов — главных компонент, каждый из которых представляет линейную комбинацию исходных признаков. Вторая главная компонента F2 строится с таким расчетом, чтобы ее направление было ортогонально направлению F1 и она объясняла как можно большую часть остаточной дисперсии, и т.д. вплоть до n-й главной компоненты Fm. Так как выделение главных компонент происходит в убывающем порядке с точки зрения доли объясняемой ими дисперсии, то признаки, входящие в первую главную компоненту с большими коэффициентами 
оказывают максимальное влияние на дифференциацию изучаемых объектов.
Формально задача об одновременной группировке параметров и выделении существенных факторов заключается в максимизации как по разбиению параметров на множества {A1,…,Ak} так и по выбору факторов {F1,…,Fk} одного из двух критериев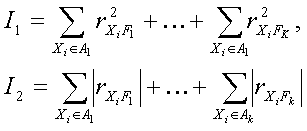 
, где 
коэффициент корреляции между признаком Xi р-й группы и соответствующей ей фактором Fp, где р =1,… ,k. Taким образом, в первом случае максимируется сумма квадратов коэффициентов корреляции признаков каждой группы со своим фактором, а во втором случае — сумма модулей этих коэффициентов.
Характеризуя особенности этого метода, укажем, что факторы F1,…,Fk, здесь не общие для всех признаков; каждый из них соответствует 'своей' группе признаков. Результаты факторного анализа будут успешными, если удается дать содержательную интерпретацию выявленных факторов, исходя из смысла показателей, характеризующих эти факторы.
Удобным инструментарием для проведения факторного анализа является пакет SPSS. При представлении результатов факторного анализа в графическом виде можно получить следующее изображение. Каждым признак имеет цвет фактора, к которому принадлежит.
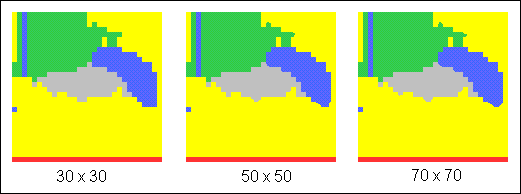
Заключение
Увеличение размерности входной информации дает более сглаженные очертания зон факторов, но участки имеют такое же расположение, следовательно, приблизительно такую же повернутую матрицу компонентов. Если соотнести результат факторного анализа и образцы обучающей выборки, то можно заметить следующее:
— фактор 4. Критерии данной области относятся непосредственно к наблюдаемому объекту;
и 
— факторы 2 и 3 соответственно. Области перехода от наблюдаемого объекта к фону;
— фактор 1. Признаки данной области относятся к фону изображения (покров);
— фактор 5. Возможные артефакты изображения. Некоторые входные образы содержали полосу снизу.
Проинтерпретировав результаты факторного анализа, можно сделать следующие выводы:
- В алгоритме обучения или классификации произвести усиление влияния признаков фактора 4;
- Частично сократить (или уменьшить влияние) признаков фактора 1;
- Дополнить обучающий набор примерами, где более четко отслеживаются признаки факторов 2 и 3;
- Исключить признаки фактора 5 в обучающем наборе.
Дополнительная информация
Автор: sermal
