Почему с помощью обычного полнотекстового поиска сложно искать очень короткие документы и как быть, если хочется это сделать.
Введение
Мы все постоянно сталкиваемся с так называемым полнотекстовым поиском — нахождением документов по поисковой фразе. Самый известный пример — это поиск Google.
Существует немало инструментов для построения полнотекстового поиска документов. Достаточно популярным решением является, например, Elasticsearch. На его основе можно организовать поиск по огромным базам данных с десятками миллионов документов.
Мы в DD Planet разрабатываем сервисы поиска и аналитики по базам данных B2B-закупок и активно используем Elasticsearch. Но когда мы попытались организовать поиск и сопоставление очень коротких документов (наименований товаров), то столкнулись с рядом проблем.
Как работает полнотекстовый поиск
Большинство систем полнотекстового поиска, в том числе и Elasticsearch, основаны на обратном индексе — структуре данных, где для каждого слова из базы документов хранятся все документы, в которых оно встречается. Обратный индекс используется для поиска по текстам.
Пусть у нас есть корпус из базы из трех текстов:
T0="синяя ручка»",
T1="синее дерево",
T2="красное дерево",тогда обратный индекс будет выглядеть следующим образом:
"синий": {0, 1}
"ручка": {0}
"дерево": {1, 2}
"красный": {2}Поиск по одному слову очевиден — это просто список всех документов, соответствующих поисковому слову. При поиске фразы можно производить как пересечение, так объединение результатов поиска по отдельным словам с целью ранжировать результаты по релевантности. Рассмотрим, например, поиск фразы «красная ручка». Поиск по слову «красный» дает результат {2}, по слову «ручка» — {0}. Пересечение пусто, поэтому точно совпадения нет. Если считать частичное совпадение, то получится два документа {0, 2} c степенью соответствия ½. В реальных поисковых системах обычно применяются более сложные методики ранжирования, например, с учетом TF-IDF, однако в результаты выдачи не может попасть документ без текстового совпадения с поисковым запросом.
Проблемы полнотекстового поиска
Если нам необходимо не просто искать внутри данных, а сопоставлять их, находить похожую информацию или те же данные, только написанные по-другому, то мы сталкиваемся со следующими проблемами:
- Контекстная значимость слов.
Вернемся к предыдущему примеру: словосочетания «синяя ручка» и «красное дерево» отличаются от фразы «красная ручка» одинаково одним слово, имеют примерно одну релевантность, однако семантически «красная ручка» намного ближе к «синей ручке», чем к «красному дереву». На мой взгляд, с этим сложнее всего бороться.
Можно применить технику с весами слов в поисковом запросе. Но такое решение переводит одну задачу в другую: непонятно, как определить эти веса адекватно. Самым простым вариантом является, как уже отмечалось, вычисление TF-IDF, но этот подход как минимум не учитывает порядка слов. - Разное написание одинаковых по значению слов.
Другая проблема — сокращения и синонимы в наименованиях товарных позиций, например, не только «лист бумаги А4», а также «А4», «бумага для принтера», «лист А4» и т. д.
Решение проблемы — загрузка в Elasticsearch словарей синонимов. Однако сборка обширных библиотек синонимов если и реальна, то очень трудоемка, особенно в узкоспециализированных областях. - Разное значение одинаковых по написанию слов.
Обратной проблемой является то, что исходя из контекста слова могут иметь разное значение. Например, во фразах «ключ дверной» и «ключ активации Windows» слово «ключ» имеет совершенно разное значение.
NLP как решение проблем
Одним из технологичных способов решить вышеупомянутые задачи является применение NLP подходов. NLP (Natural Language Processing) — общее направление искусственного интеллекта и математической лингвистики, которое изучает проблемы компьютерного анализа и синтеза естественных языков.
NLP использует семантико-синтаксический анализ введенного текста, учитывает естественно-языковые средства. Сейчас существует множество готовых моделей, фреймворков и уже решенных проблем в этой области.
Как определить степень «похожести» фраз
В NLP есть следующая задача — Paraphrase Identification — это изучение двух текстовых объектов (например, предложений) и определения, имеют ли они одинаковое значение (то есть являются парафразами). Пример парафраз: «Завтра кафе работает до 17:00» и «На следующий день кафетерий будет работать до пяти вечера». Почему это нам интересно? С помощью парафразирования мы можем анализировать текстовые описания товаров и выяснять, связаны ли они с одним товаром или нет.
Эта задача хорошо исследована. Существуют большие базы данных парафраз на русском и английском языках. В качестве инструмента для решения этой проблемы мы обратились к библиотеке DeepPavlov.ai [1], мощному фреймворку, разработанному в МФТИ. В нем собраны различные подходы и модели, связанные с обработкой русского языка.
Следующим шагом было получение базы парафраз. Так как наша тематика достаточна специфична (поиск товаров), нам нужна собственная база данных. Мы воспользовались агрегаторами магазинов вида Яндекс.Маркета. Взяли одно название товара с Маркета и другое название этого же товара в интернет-магазине.
Экспериментируя с разными моделями, имеющимися в DeepPavlov, мы поняли — основной вклад в результат дают не настройки модели, а качество наших данных.
Как организовать поиск, когда у нас почти ничего нет
Однако нам нужно не просто определять степени соответствия, а находить наиболее похожие товары. Как это сделать? Можно использовать полный перебор, однако он имеет сложность поиска $inline$O(N)$inline$ и занимает много времени, тогда как обратный индекс Elasticsearch имеет сложность поиска $inline$O(log N)$inline$. Попробуем достичь такой же скорости поиска.
Что мы имеем: множество строк и некоторую функцию, описывающую степень соответствия между этими строками. Будем далее называть эту функцию расстоянием.
Если покопаться в теории, можно наткнуться на следующую математическую структуру: метрическое пространство — это множество, на котором определена функция $inline$d$inline$ такая, что выполняются следующие аксиомы:
- Расстояние равно нулю только при равенстве двух объектов $inline$d(x, y) = 0$inline$, если $inline$x=y$inline$.
- Расстояние симметрично $inline$d(x, y) = d(y, x).$inline$
- Самая сложная из аксиом — неравенство треугольника $inline$d(x,z)≤ d(x,y)+d(y,z).$inline$ Это значит, что сумма расстояний не меньше, чем расстояние между крайними объектами.
Зачем нам нужна такая сложная структура? Она нужна для эффективного решения задач поиска ближайших соседей (Nearest neighbor search) — в нашем случае поиска похожих товаров. Такая задача может быть решена в метрическом пространстве с помощью структуры vantage-point tree, поиск в которой имеет асимптотику поиска $inline$O(log N)$inline$ [2]. Заметим, если бы речь шла о векторах, эта задача решилась намного проще, например, с помощью Kd-деревьев. Однако так как наши объекты более абстрактны, все гораздо сложнее.
Vantage-point tree
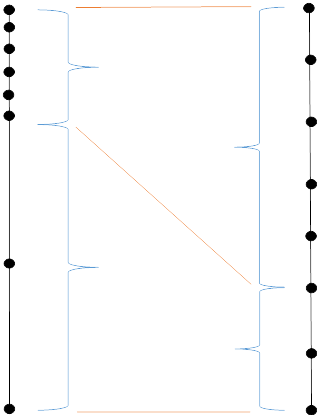
Посмотрим, как работает vantage-point tree [3]. Оно напоминает ball-tree, используемый в векторных пространствах. Его структура представляет собой бинарное дерево. Рассмотрим, как оно строится. Мы берем в качестве вершины некоторый объект из множества (vantage-point) и рисуем вокруг него окружность (изображена на рисунке ниже).
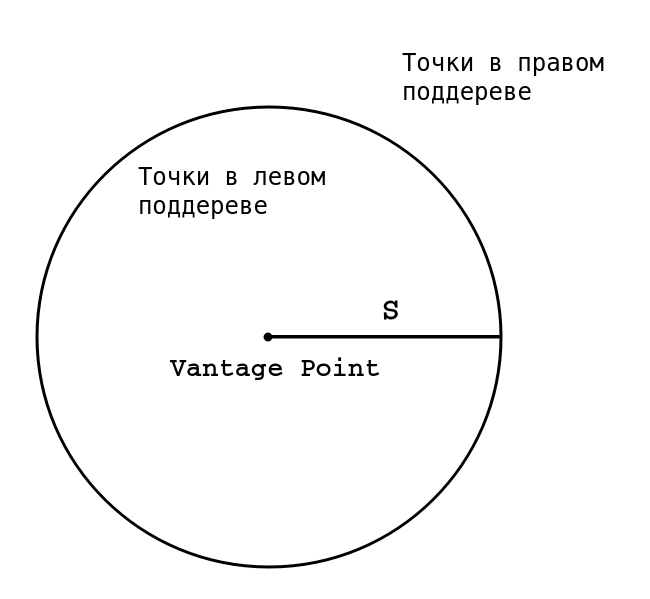
Все объекты, находящиеся внутри окружности (то есть на расстоянии $inline$≤S$inline$ от vantage-point), идут в левую часть дерева. Остальные — в правую часть. Далее процедура повторяется для каждого поддерева. Чтобы дерево было сбалансировано, надо стараться выбирать S так, чтобы исходное множество объектов делилось на примерно равные части. Это несложно сделать, если заранее просчитать все расстояния и найти их медиану.
Предположим, мы хотим найти K ближайших соседей к точке $inline$X$inline$ (отмечена красным крестиком на рисунке). Мы еще не нашли ни одной точки, поэтому в качестве ближайшего кандидата берем вершину дерева (возможно, потом мы удалим эту точку). Запоминаем значение $inline$D$inline$ — текущее расстояние до самого дальнего кандидата. Теперь надо решить, нужно ли нам искать в обоих поддеревьях или достаточно проверить только одно и них.
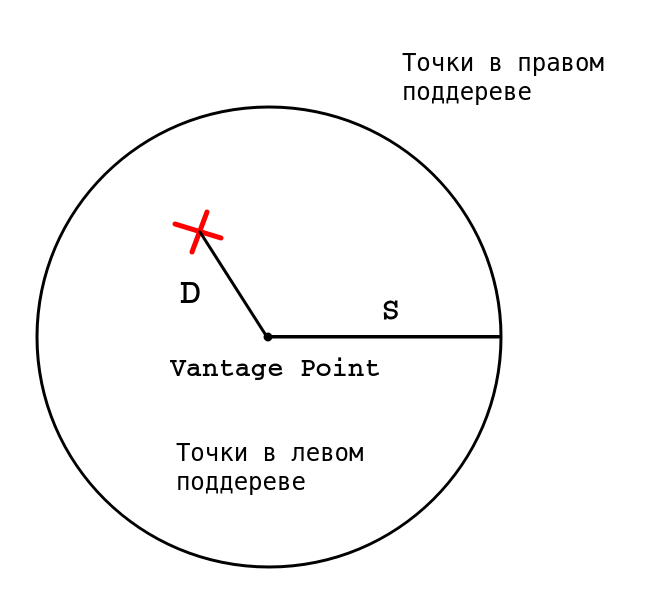
Так как точка $inline$X$inline$ находится внутри нашей окружности, мы должны сначала проверить «внутреннее» поддерево. Находим в этом поддереве синюю точку и обновляем $inline$D$inline$. Надо ли нам проверять «внешнее» поддерево? Мы рассмотрели все точки внутри окружности, но так как $inline$D > T$inline$ (расстояние от X до окружности), за пределами окружности могут существовать более близкие точки. Значит, нам надо проверить «внешнее» поддерево.
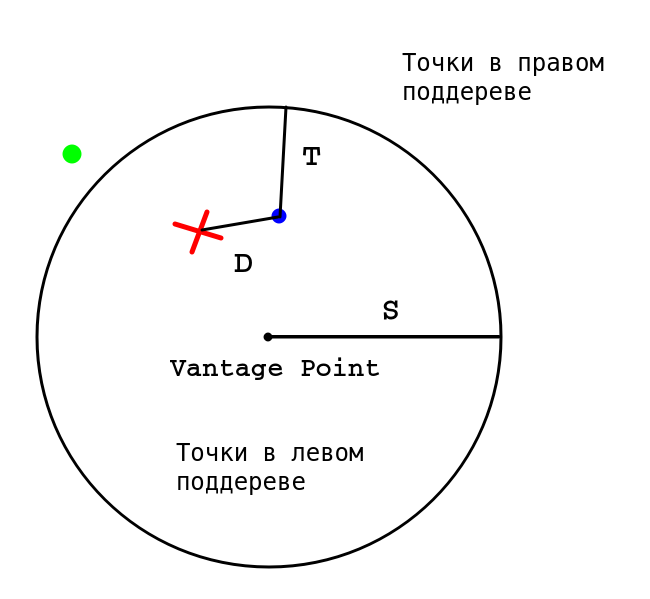
Однако если мы уже собрали K ближайших точек, а $inline$D ≤ T$inline$, то проверять «внешнее» поддерево нет необходимости. Это и обеспечивает выигрыш в производительности по сравнению с полным перебором.
Метрическая функция
Мы решили использовать нашу функцию парафразирования $inline$left(f(x,y)right)$inline$ в качестве расстояния для построения vantage-point tree и столкнулись с рядом проблем:
-
Не выполняется первая аксиома — расстояние между точками равно нулю только при условии, что они равны. Это условие не выполняется уже на обучающей выборке, так как мы полагали, что некоторые фразы означают одно и то же при их разном написании. Для решения проблемы мы добавили к основному расстоянию cosine расстояние по Doc2Vec с небольшим весом — оно будет гарантировано различно для разных объектов.
$$display$$d(x,y)=f(x,y)+ε cdot S_{Doc2Vec}(x cdot y )$$display$$
Однако вопрос подбора весового коэффициента ε остается открытым — с этим надо экспериментировать на реальных данных.
-
Модель несимметрична. Почему? Понять это достаточно сложно, но, скорее всего, проблема в ошибке округления float32. Из-за сложности модели ошибка накапливается в слоях нейронов. Эта проблема легко решается вычислением сначала расстояния от $inline$x$inline$ до $inline$y$inline$, а потом наоборот, и суммированием результата.
$$display$$d(x,y)=f(x,y)+f(y,x)$$display$$
-
Не всегда выполняется неравенство треугольника $inline$d(x,z)≤ d(x,y)+d(y,z)$inline$. Причиной этого являются особенности обучения нашей модели парафразирования. Например, рассмотрим фразы
x="красная машина", y="синяя машина", z="синий микроавтобус"Это наглядный пример, когда $inline$d(x,z) ≥ d(x,y)+d(y,z).$inline$ Из-за этого поисковая выдача иногда получается неупорядоченной. Исправить аналитически это не получается, но компенсировать это может увеличение веса расстояния Doc2Vec — для него неравенство треугольника выполняется всегда.
Выполнив формальные критерии, описанные выше, мы столкнулись на практике с другой проблемой — время поиска росло линейно, а не логарифмически, как мы ожидали. Покопавшись в литературе, мы выяснили: логарифмическая скорость поиска имеет место для примерно равномерного распределения точек в пространстве [2]. А у нас объекты распределены неравномерно — они чаще дальше, чем ближе.
Поэтому нам пришла следующая идея. Посчитаем все возможные пары расстояний и нанесем их на график (на рисунке слева). Если мы растянем верхнюю часть графика, а нижнюю сожмем, то точки будут распределены примерно одинаково (как показано на рисунке справа). Заметим, что порядок в множестве расстояний от такого преобразования не изменится. Можно при необходимости увеличить количество интервалов и получить «идеальное» распределение расстояний.
Итоги
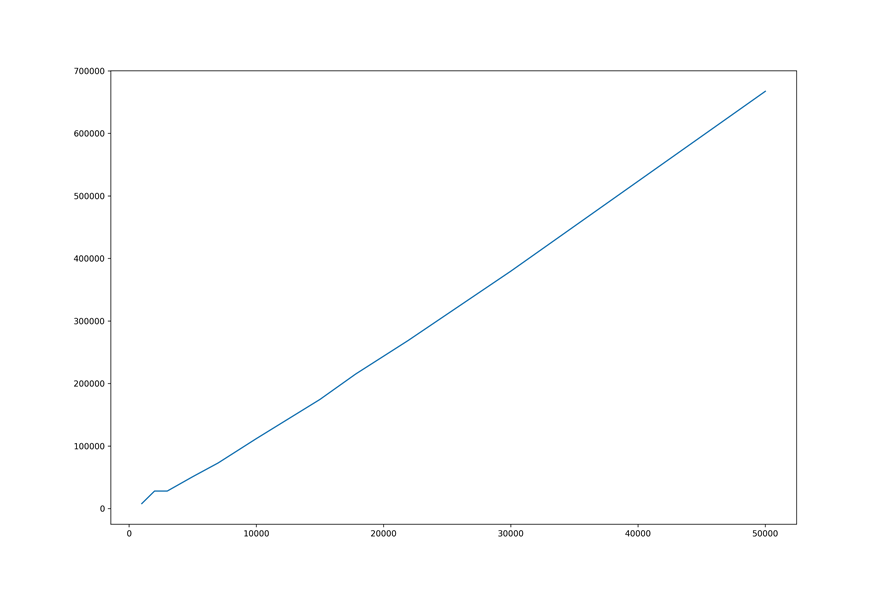
Пока что мы проводили тестирование на небольших базах данных (до миллиона объектов), и там наш поиск работает достаточно хорошо. Время сборки дерева растет практически линейно с небольшим логарифмическим коэффициентом.
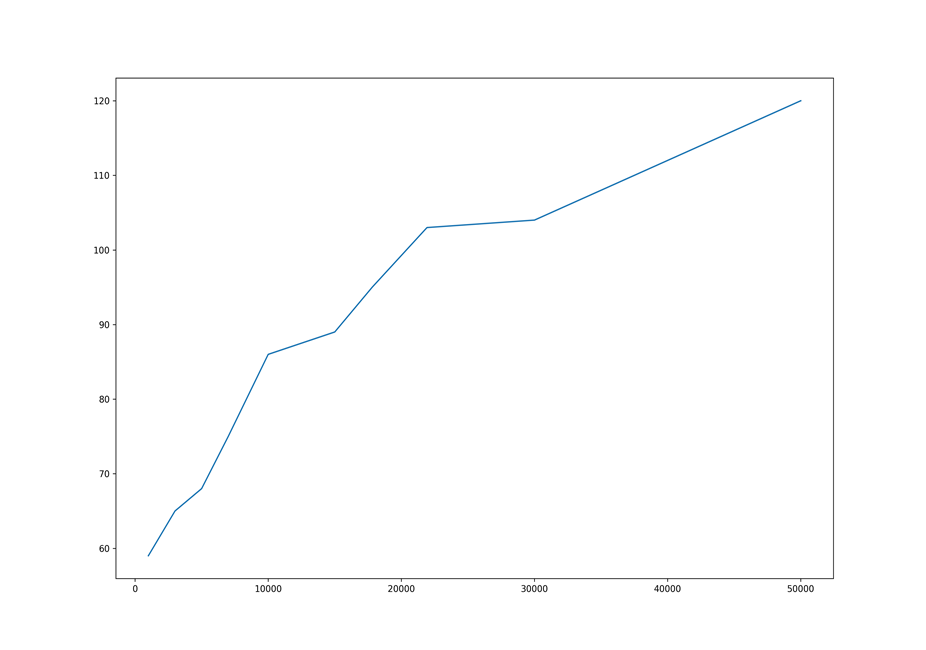
Рост времени поиска близок к логарифмическому. Почему рост времени поиска не всегда равномерен? Дело в том, что работа поиска зависит от распределения точек в пространстве. Возникает интересный вопрос: если бы мы могли управлять распределением точек в пространстве, то какое распределение было бы оптимальным? В литературе по vantage-point tree этот вопрос обычно не обсуждается, но обсуждается смежный вопрос — как оптимально выбрать vantage-point.
Например, в метрическом пространстве нужно брать самую крайнюю точку[2], тогда на границе будет меньше всего точек и поиск станет лучше. Но эта идея реализуема только в пространстве с понятиями лево, право и край. В пространстве без порядка объектов эта идея не работает.
Наше решение не является «серебряной пулей». Мы пробовали его для поиска товаров, и получилось отлично. Если выбрать другую тематику, результаты могут быть совершенно другими.
Сейчас мы работаем над развитием и оптимизацией технологии. Мы хотим создать не просто алгоритмические или математические структуры, а реально работающие поисковые системы. Текущие результаты можно посмотреть на GitHub или попробовать через pip install nlp-text-search.
Литература
[1] http://docs.deeppavlov.ai/en/master/.
[2] Yianilos (1993). Data structures and algorithms for nearest neighbor search in general metric spaces. Fourth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. pp. 311–321. pny93. http://web.cs.iastate.edu/~honavar/nndatastructures.pdf.
[3] http://stevehanov.ca/blog/?id=130
Автор: Басалов Юрий






