Вступление
Эта статья описывает стабильный нерекурсивный адаптивный алгоритм сортировки слиянием под названием quadsort.
Четверной обмен
В основе quadsort лежит четверной обмен. Традиционно большинство алгоритмов сортировки разработаны на основе бинарного обмена, где две переменные сортируются с помощью третьей временной переменной. Обычно это выглядит следующим образом:
if (val[0] > val[1])
{
tmp[0] = val[0];
val[0] = val[1];
val[1] = tmp[0];
}В четверном обмене происходит сортировка с помощью четырёх подменных переменных (своп). На первом этапе четыре переменные частично сортируются в четыре своп-переменные, на втором этапе они полностью сортируются обратно в четыре исходные переменные.
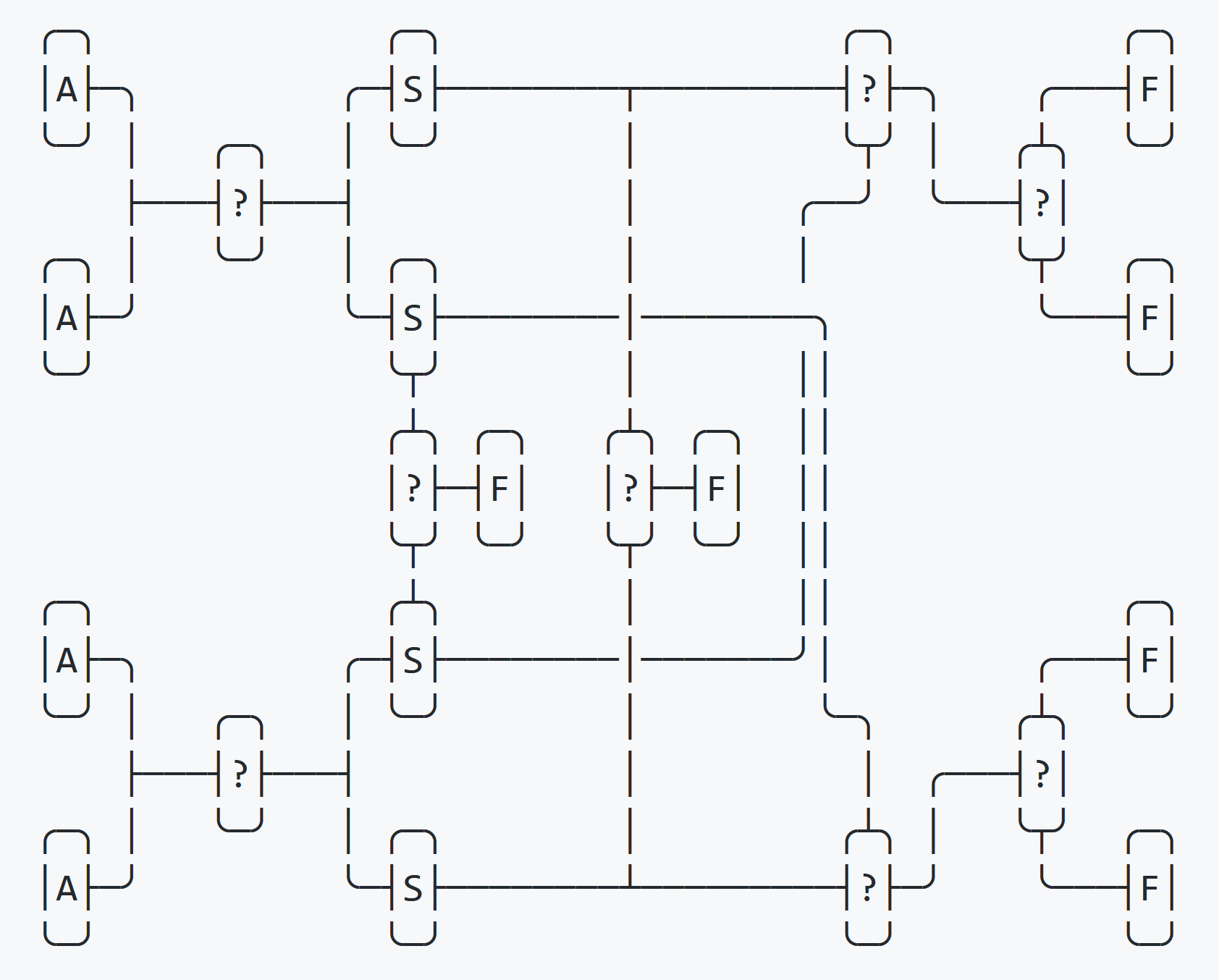
Этот процесс показан на диаграмме выше.
После первого раунда сортировки одна проверка if определяет, отсортированы ли четыре своп-переменные по порядку. Если это так, то обмен завершается немедленно. Затем проверяется, отсортированы ли своп-переменные в обратном порядке. Если это так, то сортировка завершается немедленно. Если обе проверки дают отрицательный результат, то окончательное расположение известно и остаются две проверки для определения окончательного порядка.
Это исключает одно лишнее сравнение для последовательностей, который располагаются по порядку. В то же время создаётся одно дополнительное сравнение для случайных последовательностей. Однако в реальном мире мы редко сравниваем действительно случайные данные. Поэтому когда данные скорее упорядочены, чем беспорядочны, этот сдвиг в вероятности даёт преимущество.
Существует также общее повышение производительности за счёт исключения расточительного свопа. На языке C базовый четверной своп выглядит следующим образом:
if (val[0] > val[1])
{
tmp[0] = val[1];
tmp[1] = val[0];
}
else
{
tmp[0] = val[0];
tmp[1] = val[1];
}
if (val[2] > val[3])
{
tmp[2] = val[3];
tmp[3] = val[2];
}
else
{
tmp[2] = val[2];
tmp[3] = val[3];
}
if (tmp[1] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[1];
val[2] = tmp[2];
val[3] = tmp[3];
}
else if (tmp[0] > tmp[3])
{
val[0] = tmp[2];
val[1] = tmp[3];
val[2] = tmp[0];
val[3] = tmp[1];
}
else
{
if (tmp[0] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[2];
}
else
{
val[0] = tmp[2];
val[1] = tmp[0];
}
if (tmp[1] <= tmp[3])
{
val[2] = tmp[1];
val[3] = tmp[3];
}
else
{
val[2] = tmp[3];
val[3] = tmp[1];
}
}В случае, если массив не может быть идеально разделён на четыре части, хвост из 1-3 элементов сортируется с помощью традиционного бинарного обмена.
Описанный выше четверной обмен реализован в quadsort.
Четверное слияние
На первом этапе четверной обмен предварительно сортирует массив на четырёхэлементные блоки, как описано выше.
На втором этапе используется похожий подход для обнаружения упорядоченных и обратных порядков, но в блоках по 4, 16, 64 или более элементов этот этап обрабатывается как традиционная сортировка слиянием.
Это можно представить следующим образом:
main memory: AAAA BBBB CCCC DDDD
swap memory: ABABABAB CDCDCDCD
main memory: ABCDABCDABCDABCDВ первой строке четверной обмен используется для создания четырёх блоков по четыре отсортированных элемента в каждом. Во второй строке используется четверное слияние для объединения в два блока по восемь отсортированных элементов каждый в своп-памяти. В последней строке блоки объединяются обратно в основную память, и мы остаемся с одни блоком из 16 отсортированных элементов. Ниже приводится визуализация.

Эти операции действительно требуют удвоения памяти для свопа. Подробнее об этом позже.
Пропуск
Ещё одно отличие заключается в том, что из-за возросшей стоимости операций слияния выгодно проверить, находятся ли четыре блока в прямом или обратном порядке.
В случае, если четыре блока упорядочены, операция слияния пропускается, так как является бессмысленной. Однако это требует дополнительной проверки if, и для случайно отсортированных данных эта проверка if становится всё более маловероятной по мере увеличения размера блока. К счастью, частота этой проверки if уменьшается вчетверо каждый цикл, в то время как потенциальная выгода каждый цикл увеличивается вчетверо.
В случае, если четыре блока находятся в обратном порядке, выполняется стабильный своп на месте.
В том случае, если только два из четырёх блоков упорядочены или находятся в обратном порядке, сравнения в самом слиянии излишни и впоследствии опускаются. Данные всё ещё нужно скопировать в своп-память, но это менее вычислительная процедура.
Это позволяет алгоритму quadsort сортировать последовательности в прямом и обратном порядке, используя n сравнений вместо n * log n сравнений.
Проверки границ
Ещё одна проблема с традиционной сортировкой слиянием заключается в том, что она тратит ресурсы на лишние проверки границ. Это выглядит следующим образом:
while (a <= a_max && b <= b_max)
if (a <= b)
[insert a++]
else
[insert b++]
Для оптимизации наш алгоритм сравнивает последний элемент последовательности A с последним элементом последовательности B. Если последний элемент последовательности A меньше последнего элемента последовательности B, то мы знаем, что проверка b < b_max всегда будет ложной, потому что последовательность A первой полностью сливается.
Аналогично, если последний элемент последовательности A больше последнего элемента последовательности B, мы знаем, что проверка a < a_max всегда будет ложной. Это выглядит следующим образом:
if (val[a_max] <= val[b_max])
while (a <= a_max)
{
while (a > b)
[insert b++]
[insert a++]
}
else
while (b <= b_max)
{
while (a <= b)
[insert a++]
[insert b++]
}Слияние хвоста
При сортировке массива из 65 элементов вы в конечном итоге получаете сортированный массив из 64 элементов и сортированный массив из одного элемента в конце. Это не приведёт к дополнительной операции свопа (обмена), если вся последовательность в порядке. В любом случае, для этого программа должна выбрать оптимальный размер массива (64, 256 или 1024).
Другая проблема заключается в том, что неоптимальный размер массив приводит к лишним операциям обмена. Чтобы обойти эти две проблемы, процедура четверного слияния прерывается, когда размер блока достигает 1/8 размера массива, а остальная часть массива сортируется с помощью слияния хвоста. Основное преимущество слияния хвоста заключается в том, что оно позволяет сократить объём свопа quadsort до n/2 без существенного влияния на производительность.
Big O
| Название | Лучший | Средний | Худший | Стабильный | Память |
|---|---|---|---|---|---|
| quadsort | n | n log n | n log n | да | n |
Когда данные уже отсортированы или отсортированных в обратном порядке, quadsort совершает n сравнений.
Кэш
Поскольку quadsort использует n/2 объёма своп-памяти, использование кэша не так идеально, как сортировка на месте. Однако сортировка случайных данных на месте приводит к неоптимальному обмену. Основываясь на моих бенчмарках, quadsort всегда быстрее, чем сортировка на месте, если массив не переполняет кэш L1, который на современных процессорах может достигать 64 КБ.
Wolfsort
Wolfsort — это гибридный алгоритм сортировки radixsort/quadsort, который улучшает производительность при работе со случайными данными. Это в основном доказательство концепции, которое работает только с беззнаковыми 32-и 64-битными целыми числами.
Визуализация
В приведённой ниже визуализации выполняются четыре теста. Первый тест основан на случайном распределении, второй — на распределении по возрастанию, третий — на распределении по убыванию, четвёртый — на распределении по возрастанию со случайным хвостом.
Верхняя половина показывает своп, а нижняя — основную память. Цвета различаются для операций пропуска, свопа, слияния и копирования.
Бенчмарк: quadsort, std::stable_sort, timsort, pdqsort и wolfsort
Следующий бенчмарк был запущен на конфигурации WSL gcc версии 7.4.0 (Ubuntu 7.4.0-1ubuntu1~18.04.1). Исходный код скомпилирован командой g++ -O3 quadsort.cpp. Каждый тест выполнен сто раз, и сообщается только о лучшем запуске.
По оси абсцисс время выполнения.
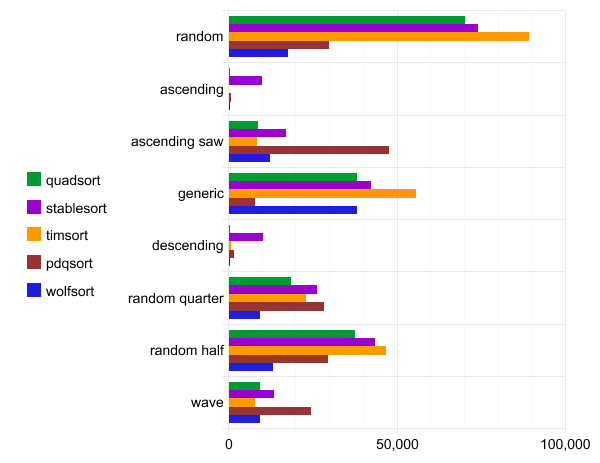
| Название | Элементов | Тип | Лучший | Средний | Сравнений | Порядок |
|---|---|---|---|---|---|---|
| quadsort | 1000000 | i32 | 0.070469 | 0.070635 | случайный порядок | |
| stablesort | 1000000 | i32 | 0.073865 | 0.074078 | случайный порядок | |
| timsort | 1000000 | i32 | 0.089192 | 0.089301 | случайный порядок | |
| pdqsort | 1000000 | i32 | 0.029911 | 0.029948 | случайный порядок | |
| wolfsort | 1000000 | i32 | 0.017359 | 0.017744 | случайный порядок | |
| quadsort | 1000000 | i32 | 0.000485 | 0.000511 | возрастание | |
| stablesort | 1000000 | i32 | 0.010188 | 0.010261 | возрастание | |
| timsort | 1000000 | i32 | 0.000331 | 0.000342 | возрастание | |
| pdqsort | 1000000 | i32 | 0.000863 | 0.000875 | возрастание | |
| wolfsort | 1000000 | i32 | 0.000539 | 0.000579 | возрастание | |
| quadsort | 1000000 | i32 | 0.008901 | 0.008934 | возрастание ступеньками (пилой) | |
| stablesort | 1000000 | i32 | 0.017093 | 0.017275 | возрастание ступеньками (пилой) | |
| timsort | 1000000 | i32 | 0.008615 | 0.008674 | возрастание ступеньками (пилой) | |
| pdqsort | 1000000 | i32 | 0.047785 | 0.047921 | возрастание ступеньками (пилой) | |
| wolfsort | 1000000 | i32 | 0.012490 | 0.012554 | возрастание ступеньками (пилой) | |
| quadsort | 1000000 | i32 | 0.038260 | 0.038343 | нормальный порядок | |
| stablesort | 1000000 | i32 | 0.042292 | 0.042388 | нормальный порядок | |
| timsort | 1000000 | i32 | 0.055855 | 0.055967 | нормальный порядок | |
| pdqsort | 1000000 | i32 | 0.008093 | 0.008168 | нормальный порядок | |
| wolfsort | 1000000 | i32 | 0.038320 | 0.038417 | нормальный порядок | |
| quadsort | 1000000 | i32 | 0.000559 | 0.000576 | убывание | |
| stablesort | 1000000 | i32 | 0.010343 | 0.010438 | убывание | |
| timsort | 1000000 | i32 | 0.000891 | 0.000900 | убывание | |
| pdqsort | 1000000 | i32 | 0.001882 | 0.001897 | убывание | |
| wolfsort | 1000000 | i32 | 0.000604 | 0.000625 | убывание | |
| quadsort | 1000000 | i32 | 0.006174 | 0.006245 | убывание ступеньками | |
| stablesort | 1000000 | i32 | 0.014679 | 0.014767 | убывание ступеньками | |
| timsort | 1000000 | i32 | 0.006419 | 0.006468 | убывание ступеньками | |
| pdqsort | 1000000 | i32 | 0.016603 | 0.016629 | убывание ступеньками | |
| wolfsort | 1000000 | i32 | 0.006264 | 0.006329 | убывание ступеньками | |
| quadsort | 1000000 | i32 | 0.018675 | 0.018729 | случайный хвост | |
| stablesort | 1000000 | i32 | 0.026384 | 0.026508 | случайный хвост | |
| timsort | 1000000 | i32 | 0.023226 | 0.023395 | случайный хвост | |
| pdqsort | 1000000 | i32 | 0.028599 | 0.028674 | случайный хвост | |
| wolfsort | 1000000 | i32 | 0.009517 | 0.009631 | случайный хвост | |
| quadsort | 1000000 | i32 | 0.037593 | 0.037679 | случайная половина | |
| stablesort | 1000000 | i32 | 0.043755 | 0.043899 | случайная половина | |
| timsort | 1000000 | i32 | 0.047008 | 0.047112 | случайная половина | |
| pdqsort | 1000000 | i32 | 0.029800 | 0.029847 | случайная половина | |
| wolfsort | 1000000 | i32 | 0.013238 | 0.013355 | случайная половина | |
| quadsort | 1000000 | i32 | 0.009605 | 0.009673 | распределение волнами | |
| stablesort | 1000000 | i32 | 0.013667 | 0.013785 | распределение волнами | |
| timsort | 1000000 | i32 | 0.007994 | 0.008138 | распределение волнами | |
| pdqsort | 1000000 | i32 | 0.024683 | 0.024727 | распределение волнами | |
| wolfsort | 1000000 | i32 | 0.009642 | 0.009709 | распределение волнами |
Следует отметить, что pdqsort не является стабильной сортировкой, поэтому он быстрее работает с данными в обычном порядке (общий порядок).
Следующий бенчмарк запускался на WSL gcc версии 7.4.0 (Ubuntu 7.4.0-1ubuntu1~18.04.1). Исходный код скомпилирован командой g++ -O3 quadsort.cpp. Каждый тест выполнен сто раз, и сообщается только о лучшем запуске. Он измеряет производительность на массивах размером от 675 до 100 000 элементов.
Ось X приведённого ниже графика — это количество элементов, ось Y — время выполнения.
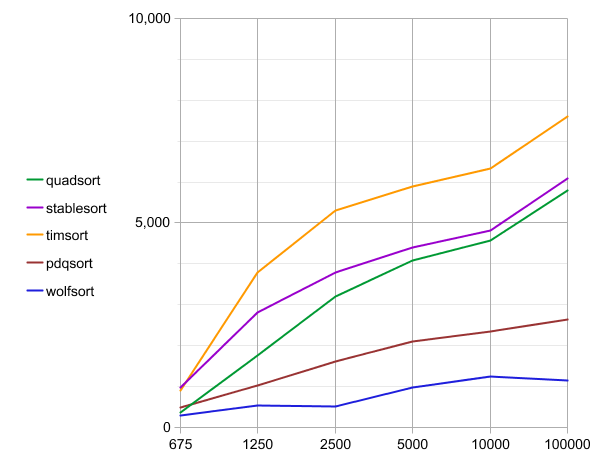
| Название | Элементов | Тип | Лучший | Средний | Сравнений | Порядок |
|---|---|---|---|---|---|---|
| quadsort | 100000 | i32 | 0.005800 | 0.005835 | случайный порядок | |
| stablesort | 100000 | i32 | 0.006092 | 0.006122 | случайный порядок | |
| timsort | 100000 | i32 | 0.007605 | 0.007656 | случайный порядок | |
| pdqsort | 100000 | i32 | 0.002648 | 0.002670 | случайный порядок | |
| wolfsort | 100000 | i32 | 0.001148 | 0.001168 | случайный порядок | |
| quadsort | 10000 | i32 | 0.004568 | 0.004593 | случайный порядок | |
| stablesort | 10000 | i32 | 0.004813 | 0.004923 | случайный порядок | |
| timsort | 10000 | i32 | 0.006326 | 0.006376 | случайный порядок | |
| pdqsort | 10000 | i32 | 0.002345 | 0.002373 | случайный порядок | |
| wolfsort | 10000 | i32 | 0.001256 | 0.001274 | случайный порядок | |
| quadsort | 5000 | i32 | 0.004076 | 0.004086 | случайный порядок | |
| stablesort | 5000 | i32 | 0.004394 | 0.004420 | случайный порядок | |
| timsort | 5000 | i32 | 0.005901 | 0.005938 | случайный порядок | |
| pdqsort | 5000 | i32 | 0.002093 | 0.002107 | случайный порядок | |
| wolfsort | 5000 | i32 | 0.000968 | 0.001086 | случайный порядок | |
| quadsort | 2500 | i32 | 0.003196 | 0.003303 | случайный порядок | |
| stablesort | 2500 | i32 | 0.003801 | 0.003942 | случайный порядок | |
| timsort | 2500 | i32 | 0.005296 | 0.005322 | случайный порядок | |
| pdqsort | 2500 | i32 | 0.001606 | 0.001661 | случайный порядок | |
| wolfsort | 2500 | i32 | 0.000509 | 0.000520 | случайный порядок | |
| quadsort | 1250 | i32 | 0.001767 | 0.001823 | случайный порядок | |
| stablesort | 1250 | i32 | 0.002812 | 0.002887 | случайный порядок | |
| timsort | 1250 | i32 | 0.003789 | 0.003865 | случайный порядок | |
| pdqsort | 1250 | i32 | 0.001036 | 0.001325 | случайный порядок | |
| wolfsort | 1250 | i32 | 0.000534 | 0.000655 | случайный порядок | |
| quadsort | 675 | i32 | 0.000368 | 0.000592 | случайный порядок | |
| stablesort | 675 | i32 | 0.000974 | 0.001160 | случайный порядок | |
| timsort | 675 | i32 | 0.000896 | 0.000948 | случайный порядок | |
| pdqsort | 675 | i32 | 0.000489 | 0.000531 | случайный порядок | |
| wolfsort | 675 | i32 | 0.000283 | 0.000308 | случайный порядок |
Бенчмарк: quadsort и qsort (mergesort)
Следующий бенчмарк запускался на WSL gcc версии 7.4.0 (Ubuntu 7.4.0-1ubuntu1~18.04.1). Исходный код скомпилирован командой g++ -O3 quadsort.cpp. Каждый тест выполнен сто раз, и сообщается только о лучшем запуске.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 (случайный порядок)
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 (случайный порядок)
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 (возрастание)
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 (возрастание)
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 (возрастание ступенями)
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 (возрастание ступенями)
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 (общий порядок)
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 (общий порядок)
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 (убывание)
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 (убывание)
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 (убывание ступенями)
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 (убывание ступенями)
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 (случайный хвост)
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 (случайный хвост)
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 (случайная половина)
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 (случайная половина)
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 (распределение волнами)
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 (распределение волнами)
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 (стабильный)
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 (нестабильный)
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)Показатель MO указывает количество сравнений, выполненных для 1 миллиона элементов.
В приведённом выше бенчмарке quadsort сравнивается с glibc qsort() через тот же интерфейс общего назначения и без каких-либо известных несправедливых преимуществ, таких как инлайнинг.
random order: 635, 202, 47, 229, etc
ascending order: 1, 2, 3, 4, etc
uniform order: 1, 1, 1, 1, etc
descending order: 999, 998, 997, 996, etc
wave order: 100, 1, 102, 2, 103, 3, etc
stable/unstable: 100, 1, 102, 1, 103, 1, etc
random range: time to sort 1000 arrays ranging from size 0 to 999 containing random dataБенчмарк: quadsort и qsort (quicksort)
Этот конкретный тест выполнен с использованием реализации qsort() от Cygwin, которая под капотом использует quicksort. Исходный код скомпилирован командой gcc -O3 quadsort.c. Каждый тест выполнен сто раз, сообщается только о лучшем запуске.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 (случайный порядок)
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 (случайный порядок)
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 (возрастание)
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 (возрастание)
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 (возрастание ступенями)
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 (возрастание ступенями)
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 (общий порядок)
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 (общий порядок)
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 (убывание)
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 (убывание)
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 (убывание ступенями)
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 (убывание ступенями)
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 (случайный хвост)
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 (случайный хвост)
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 (случайная половина)
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 (случайная половина)
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 (распределение волнами)
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 (распределение волнами)
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 (стабильный)
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 (нестабильный)
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)В этом бенчмарке становится ясно, почему quicksort часто предпочтительнее традиционного слияния, он делает меньше сравнений для данных в возрастающем порядке, равномерно распределённых и для данных в убывающем порядке. Однако в большинстве тестов он показал себя хуже, чем quadsort. Quicksort также демонстрирует чрезвычайно низкую скорость сортировки данных, упорядоченных волнами. Тест с данными в случайном порядке показывает, что quadsort более чем в два раза быстрее при сортировке небольших массивов.
Quicksort быстрее в универсальных и стабильных тестах, но только потому, что это нестабильный алгоритм.
Автор: m1rko




