
Из всего зоопарка куч, эта структура, пожалуй, самая необычная. При этом элегантная простота алгоритма вполне под стать его удивительной неординарности.
При сортировке с помощью слабой кучи всегда меньше количество сравнений и обменов, чем если использовать обычную кучу. Так что да, слабая куча сильнее, чем обычная куча.
Статья написана при поддержке компании EDISON.Мы занимаемся созданием встроенного программного обеспечения а также разработкой веб-приложений и сайтов.
Мы очень любим теорию алгоритмов! ;-)
Слабая куча
Обычная куча представляет собой сортирующее дерево, в котором любой родитель больше (или равен) чем любой из его потомков. В слабой куче это требование ослаблено — любой родитель больше (или равен) любого потомка только из своего правого поддерева. В левом поддереве потомки могут быть и меньше и больше родителя, там уж как повезёт.
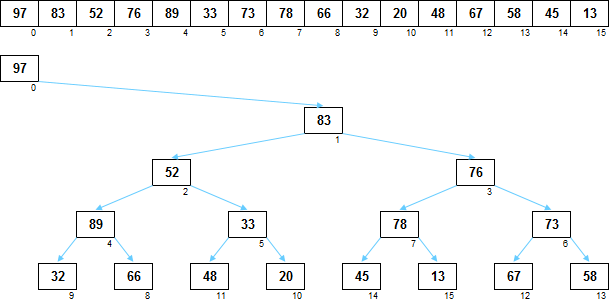
Такой подход позволяет значительно сократить издержки по поддержанию набора данных в состоянии кучи. Ведь нужно обеспечить принцип «потомок не больше родителя» не для всей структуры, а только её половины. При этом слабая куча, не являясь на 100% сортирующим деревом, сортирует не хуже обычной кучи, а в чём-то даже и лучше. Сделал полдела — гуляй смело!
Поскольку в корне кучи, даже слабой, нужен именно максимальный по величине элемент, у корня левого поддерева нет.
Минимизация количества сравнений

Слабую кучу нам подарил специалист по алгоритмам и теории графов Рональд Д. Даттон в 1993 году. Концептуально слабая куча труднее для понимания (но эта трудность заключается скорее не в сложности, а в экстравагантности, придётся ломать через колено шаблоны своего сознания), чем обычная куча, поэтому она не получила особого практического распространения. Тем не менее, когда Даттон изобрёл эту структуру, он не просто хотел поупражняться в отвлечённых абстракциях, но преследовал вполне прагматичную цель.
Есть теоретический нижний предел для оценки минимального количества сравнений (в тех сортировках, в которых эти сравнения широко используются):
log n! = n log n − n / ln 2 + O(log n), где 1 / ln 2 = 1.4426
В сортировке слабой кучей количество сравнений минимизировано и достаточно близко приближено к нижнему пределу.
Это может иметь практическое значение если нужно упорядочить объекты, сравнение которых дорого обходится, например, если речь идёт о сортировке длинных строк.
Жонглируем потомками
«Левый» и «правый» в слабой куче — явление ситуативное. Поддерево может быть для своего родительского узла как левым так и правым потомком — причём, это отношение «левый/правый» для поддерева и родителя может по ходу процесса многократно переключаться с одного значения на противоположное.
Указать для родителя кто у него правый сын, а кто левая дочь, не просто, а очень просто. Для этого нужен дополнительный битовый массив (состоящий только из значений 0/1) для тех узлов, у которых есть потомки.
Вспомним, как по индексу i-го элемента-родителя, мы определяем индексы его левого и правого потомка в обычной куче (индексы в массиве отсчитываем от нуля):
Левый потомок: 2 × i + 1
Правый потомок: 2 × i + 2
В слабой куче у нас есть вишенка на торте — корень, у которого только правое поддерево, поэтому скорректируем эти формулы для индексов потомков, добавив обратный сдвиг в 1 позицию:
Левый потомок: 2 × i
Правый потомок: 2 × i + 1
И, наконец, нужен дополнительный битовый массив (назовём его BIT), в котором для i-го элемента отмечено, был ли обмен местами между его левым и правым поддеревьями. Если значение для элемента равно 0, то значит обмена не было. Если значение равно 1, значит, левый и правый потомок идут в обратном порядке. А формулы при этом вот такие:
Левый потомок: 2 × i + BIT[i]
Правый потомок: 2 × i + 1 − BIT[i]
Вот так это выглядит. Элементы, у которых потомки расположены «наоборот», подсвечены синим. Значения в массиве BIT для них равны 1.
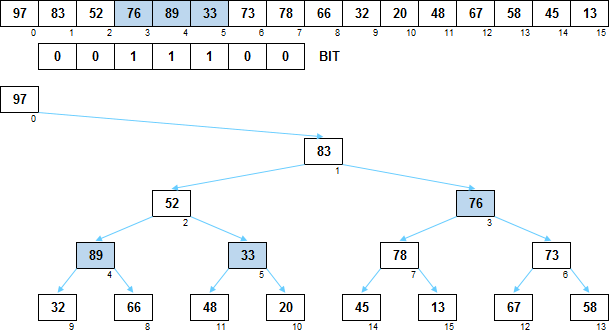
Можете проверить, подставив в формулы потомков родительские значения i и соответствующие им 0/1 из массива BIT — индексы потомков получатся такие как нужно.
Как видите, чтобы для любого родителя поменять местами левое и правое поддерево, в самом массиве группы элементов никуда передвигать не нужно. Переключается только значение 0/1 для родителя в массиве BIT и всё.
Далее — сеанс магии с её последующим разоблачением.
Строим слабую кучу
Обмен местами левого и правого потомков — основной инструмент для преобразования в слабую кучу набора данных из массива.
В процессе формирования первичной слабой кучи нам нужно в обратном порядке (начиная с последнего) перебрать элементы массива и для каждого из них найти вверх по ветке первого (пра)родителя, для которого это будет правое поддерево.
Если элемент является чьим-то правым потомком, то далеко ходить не надо. Его непосредственный родитель и является тем, что нужно:
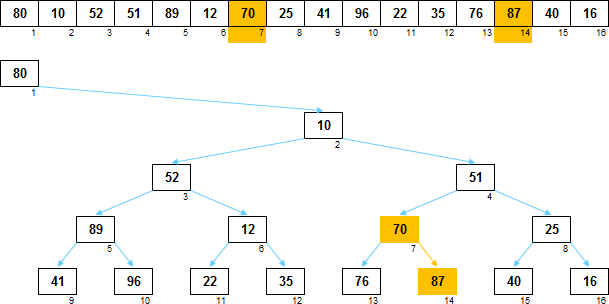
Если элемент является чьим-то левым потомком, то нужно подняться на некоторое количество уровней вверх, прежде чем встретится нужный прародитель, для которого элемент находится в правом поддереве:
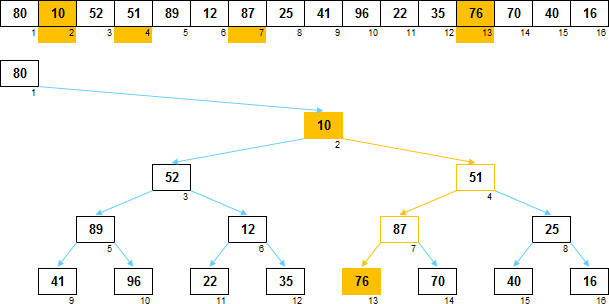
Затем нужно сравнить потомка и найденного где-то вверху прародителя. И если потомок окажется больше прародителя, то необходимо сделать следующее:
- Если у потомка есть свои потомки, то поменять местами его левое и правое поддерева (т.е. переключить 0/1 в массиве BIT для этого элемента).
- Обменять значениями узел-потомок и узел-прародитель.
Взглянем на конкретный пример. Допустим возникла вот такая вот ситуация:
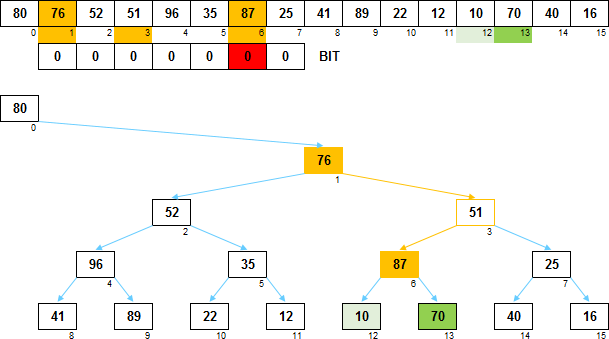
Для элемента массива A[6]=87 найден нужный прародитель A[1]=76.
Прародитель A[1] меньше элемента A[6] (76 < 87).
У элемента A[6] есть левое и правое поддеревья (отмечены оттенками зелёного).
Нужно обменять местами эти поддеревья
(т.е. для элемента A[6] в массиве BIT изменить значение с 0 на 1).
Также необходимо обменять значениями элементы A[6] и A[1].
После того как будут выполнены необходимые действия:
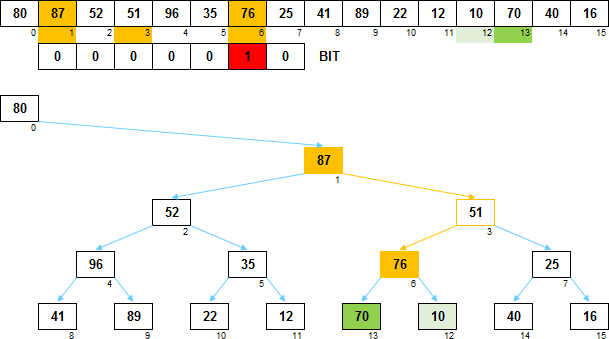
Для элемента A[6] произошёл обмен местами левого и правого поддеревьев
(т.е. в массиве BIT для элемента A[6] значение с 0 изменено на 1).
Также произошёл обмен значениями между A[6] и A[1].
Если пройти по массиву с конца в начало и по пути выполнить эту процедуру для всех элементов, то в итоге получится слабая куча.
Почему этот странный механизм работает — объяснение ближе к концу статьи.
Разбираем слабую кучу
Куча является кучей, если максимальный элемент находится в корне. Используя этот факт, все сортировки кучами работают однотипно. Корень (в котором находится максимум) обменивается значениями с последним элементом неотсортированной части массива — в результате чего неотсортированная часть массива уменьшается, а отсортированная часть массива увеличивается. После этого обмена куча перестаёт быть кучей, так как в её корне уже не находится текущий максимальный элемент. Кучу нужно восстановить, то есть сделать получившееся дерево снова кучей — найти другой максимальный элемент и переместить его в корень.
Как восстанавливается обычная бинарная куча, мы знаем — с помощью просейки. Но как восстановить слабую кучу? Для этого нужно сделать следующее.
Из корня опускаемся вниз по левым потомкам (вплоть до самого нижнего):

Затем поднимаемся по левым потомкам обратно наверх и по пути каждый левый потомок сравниваем с элементом в корне кучи. И если очередной левый потомок больше корня, то делаем то же самое что и на предыдущем этапе: у левого потомка меняем местами поддеревья (если они у него есть) и меняем значениями левый потомок и корень.
В результате мы восстановим слабую кучу — в её корень всплывёт максимальный элемент, который есть в оставшемся дереве.
И опять у нас эта мистическая карусель с поддеревьями, которые сменяют друг друга. Так в чём же секрет успеха? Почему если при обмене узлов значениями менять у нижнего узла местами левых и правых потомков, то в итоге получаем отсортированный массив? Ни за что не догадаетесь, хотя ответ прост в своей гениальности.
Сортировка слабой кучей :: Weak heap sort
Итак, итоговый алгоритм:
- I. Формируем из массива слабую кучу:
- I.1. Перебираем элементы массива слева-направо.
- I.2. Для текущего элемента поднимаемся вверх по родительской ветке до ближайшего «правого» родителя.
- I.3. Сравниваем текущий элемент и ближайшего правого родителя.
- I.4. Если ближайший правый родитель меньше текущего элемента, то:
- I.4.а. Меняем местами (левый ⇔ правый) поддеревья с потомками для узла, в котором находится текущий элемент.
- I.4.б. Меняем значениями ближайший «правый» родитель и узел с текущим элементом.
- II. Из корня кучи текущий максимальный элемент перемещаем в конец неотсортированной части массива, после чего восстанавливаем слабую кучу:
- II.1. В корне кучи находится текущий максимальный элемент для неотсортированной части массива.
- II.2. Меняем местами максимум из корня кучи и последний элемент в неотсортированной части массива. Последний элемент с максимумом перестаёт быть узлом слабой кучи.
- II.3. После этого обмена дерево перестало быть слабой кучей, так как в корне оказался не максимальный элемент. Поэтому делаем просейку:
- II.3.а. Опускаемся из корня кучи по левым потомкам как можно ниже.
- II.3.б. Поднимаемся по левым потомкам обратно к корню кучи, сравнивая каждый левый потомок с корнем.
- II.3.в. Если элемент в корне меньше, чем очередной левый потомок, то:
- II.3.в.1. Меняем местами (левый ⇔ правый) поддеревья с потомками для узла, в котором находится текущий левый потомок.
- II.3.в.2. Меняем значениями корень кучи и узел с текущим левым потомком.
- II.4. В корне слабой кучи снова находится максимальный элемент для оставшейся неотсортированной части массива. Возвращаемся в пункт II.1 и повторяем процесс, пока не будут отсортированы все элементы.
Анимация (индексы массивов в моих анимациях начинаются с единицы):

Код на C++
Внизу в разделе «Ссылки» заинтересовавшиеся смогут ознакомиться с реализацией этой сортировки на C++. Тут приведу только ту часть, которая иллюстрирует сам алгоритм.
#define GETFLAG(r, x) ((r[(x) >> 3] >> ((x) & 7)) & 1)
#define TOGGLEFLAG(r, x) (r[(x) >> 3] ^= 1 << ((x) & 7))
void WeakHeap::WeakHeapMerge(unsigned char *r, int i, int j) {
if (wheap[i] < wheap[j]) {//"Суперродитель" меньше потомка?
//Для потомка переопределяем, порядок его потомков
//(кто "левый", а кто "правый")
TOGGLEFLAG(r, j);
//Меняем значения "суперродителя" и потомка
swap(wheap[i], wheap[j]);
}
}
void WeakHeap::WeakHeapSort() {
int n = Size();
if(n > 1) {
int i, j, x, y, Gparent;
int s = (n + 7) / 8;
unsigned char * r = new unsigned char [s];
//Массив для обозначения, какой у элемента
//потомок "левый", а какой "правый"
for(i = 0; i < n / 8; ++i) r[i] = 0;
//Построение первоначальной слабой кучи
for(i = n - 1; i > 0; --i) {
j = i;
//Поднимаемся на сколько возможно вверх,
//если в качестве "левого" потомка родителя
while ((j & 1) == GETFLAG(r, j >> 1)) j >>= 1;
//И ещё на один уровень вверх как "правый" потомок родителя
Gparent = j >> 1;
//Слияние начального элемента, с которого
//начали восхождение до "суперродителя"
WeakHeapMerge(r, Gparent, i);
}
//Перенос максимума из корня в конец -->
//слабая просейка --> и всё по новой
for(i = n - 1; i >= 2; --i) {
//Максимум отправляем в конец неотсортированной части массива
//Элемент из конца неотсортированной части попадает в корень
swap(wheap[0], wheap[i]);
x = 1;
//Опускаемся жадно вниз по "левым" веткам
while((y = 2 * x + GETFLAG(r, x)) < i) x = y;
//Поднимаемся по "левой" ветке обратно до самого вверха
//попутно по дороге делаем слияние каждого узла с корнем
while(x > 0) {
WeakHeapMerge(r, 0, x);
x >>= 1;
}
}
//Последнее действие - меняем местами корень
//и следующий за ним элемент
swap(wheap[0], wheap[1]);
delete[] r;
}
}Особенно мне нравится как легко и непринуждённо происходит обход бинарного дерева с помощью битовых операций.
Сложность по дополнительной памяти
Вроде как O(n) — требуется дополнительный массив, в котором для узлов с потомками (таковых в массиве примерно половина) зафиксирован порядок левого/правого поддеревьев.
Впрочем, есть мнение, что здесь сложность у сортировки на самом деле O(1)! Для элемента нам нужен всего один дополнительный бит (нолик/единичка), чтобы указать порядок следования потомков. Если сортируем, к примеру, строки, то вполне реализуемо дописывать этот дополнительный бит к самому элементу.
Другой способ превратить O(n) в O(1) — хранить флаги в целом числе. Двоичное разложение числа — набор нулей и единиц, отвечающих за порядок поддеревьев всех элементов массива. i-й элемент массива соответствует i-му биту числа.
Сложность по времени
По времени O(n log n) — то же самое, что и у обычной кучи. При сортировке строк (особенно длинных) слабая куча может оказаться быстрее, чем обычная куча. Но это если сортируем длинные строки. Если сортируем числа, то, по слухам, обычная куча быстрее управляется.
Полная просейка вверх
На этапе формирования первоначальной слабой кучи, по аналогии с обычной кучей, напрашивается вполне очевидная идея поднимать большие элементы настолько высоко, насколько получится. То есть, если мы обменяли значениями нижний узел и его прародитель, то затем вполне логично было бы сразу повторить действия для прародителя — найти для него своего ближайшего правого прародителя и сравнить (и, если необходимо тоже обменять значениями + обмен поддеревьев). И, если получится, поднять крупный элемент в самый корень. Вот так это выглядит на первом этапе (действия на втором этап алгоритма без изменений):

Оценка сложности по времени остаётся той же.
Биномиальная куча
Всё что было до этого момента — обман, иллюзия. Конечно, формально мы там совершаем некие манипуляции с двоичным деревом, меняем узлы значениями, переставляем поддеревья и всё такое. Однако у алгоритма есть двойное дно, в которое мы сейчас заглянем.
Чтобы раскусить эту сортировку, нужно понять, чем на самом деле является слабая куча.
Если взять массив, в котором количество элементов — степень двойки, то построенные на его основе слабая куча и биномиальная куча изоморфны.
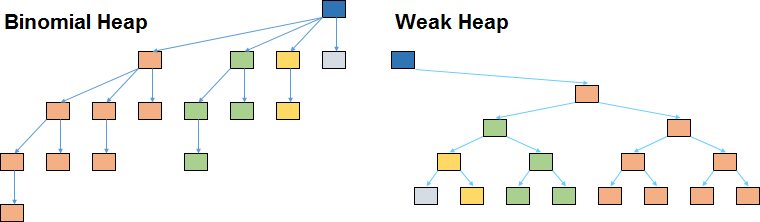
Не смотрите на то, что слабая куча является бинарной, а биномиальная — нет. В слабой куче левое и правое поддеревья разные по сути. Правое поддерево является потомком в классическом понимании, а вот левое поддерево — скорее «братом». Хотя нет. Левое поддерево является даже не «братом», а вектором «братьев» с меньшими количествами узлов.
Однако weak heap и binomial heap не на 100% одно и то же, хотя они и самые ближайшие родственники. Различие очевидно, если взять массив, количество элементов в котором не равно 2n. Биномиальное разложение такого массива даст связный список нескольких идеальных куч (количество узлов в каждой из них — некоторая степень двойки):
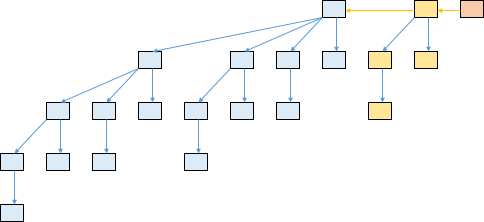
А слабая куча в этом случае будет представлять собой одно неидеальное двоичное дерево:
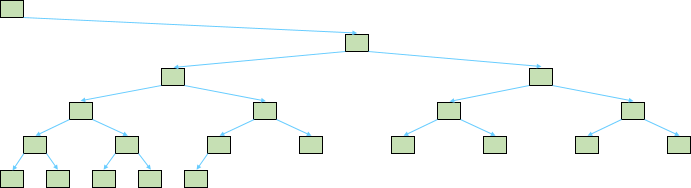
Биномиальная куча и слабая куча — это разнояйцевые близнецы. ДНК один и тот же, хотя по внешности и не скажешь.
Секрет алгоритма
С учётом того, что слабая куча — это криптобиномиальная куча, перетасовка поддеревьев внезапно обретает простое объяснение.
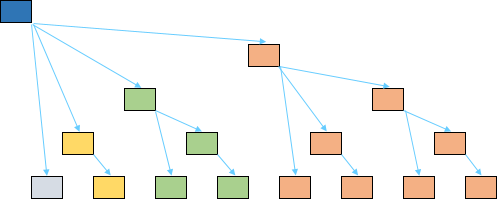
Смахнём со слабой кучи псевдобинарную мишуру и посмотрим на настоящие отношения между узлами в стиле биномиальной кучи. Всё становится ясно.
На самом деле:
- Нет никакой «ослабленности», это полноценное сортирующее (небинарное) дерево, в котором достигается и поддерживается принцип «любой родитель больше любого своего потомка».
- На всех этапах сравниваем потомков не с прародителями, а со своими непосредственными родителями.
- То что выглядит как обмен значениями между потомком и прародителем + обмен местами поддеревьев у потомка — оказывается это обмен самим соотношением (потомок/родитель). Если родительский узел по значению меньше потомка, то родитель сам становится потомком, а потомок — родителем.
Вот честная визуализация:

В следующей серии
Следующая куча, о которой бы хотелось рассказать, моя самая любимая — декартово дерево. Это не только куча, но и по совместительству бинарное дерево поиска. Но тогда сначала в следующей статье необходимо кое-что интересное про BST-деревья разъяснить. А уж потом, через статью, и про декартово поговорим.
Ссылки
![]() Weak Heap, Binomial Heap / Биномиальная куча
Weak Heap, Binomial Heap / Биномиальная куча
![]() Рональд Д. Даттон: Персональная страница, Профиль на сайте UCF
Рональд Д. Даттон: Персональная страница, Профиль на сайте UCF
![]() Weak Heaps and Friends: Recent Developments
Weak Heaps and Friends: Recent Developments
![]() The Weak-Heap Data Structure: Variants and Applications
The Weak-Heap Data Structure: Variants and Applications
![]() On the Performance of WEAK-HEAPSORT
On the Performance of WEAK-HEAPSORT
![]() Adaptive heapsort: Source code
Adaptive heapsort: Source code
![]() Сергей Копелиович — Лекториум — Слабая куча (с 48:32 по 1:16:06)
Сергей Копелиович — Лекториум — Слабая куча (с 48:32 по 1:16:06)
Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировки выбором
- Сортировки кучей: n-нарные пирамиды
- Сортировки кучей: числа Леонардо
- Сортировки кучей: слабая куча
- Сортировки кучей: декартово дерево
- Прочие сортировки кучей: зеркальная куча, мини-куча, просейка снизу-вверх
- Сортировки кучей: юнгова куча
- Сортировки слиянием
- Сортировки распределением
- Гибридные сортировки
В приложение AlgoLab добавлена сегодняшняя сортировка слабой кучей, кто пользуется — обновите excel-файл с макросами.
В комментариях к ячейке с название сортировки можно указать кое-какие настройки. Если прописать siftup=1 то в сортировке будет использована полная просейка вверх на первом этапе (по умолчанию siftup=0).
Если прописать binomial=1 то дерево будет а-ля «биномиальная куча» (по умолчанию binomial=0, то есть просто слабая куча).
Автор: Валерий Макаров


