
Предисловие
Существует такой тип людей, для которых исследования и создание сложных и функциональных систем — высшая степень удовольствия. К такому типу можно отнести и меня. Любой целостный объект, обладающий единством всей своей структуры, материального, социального и абстрактного миров обладает системностью: человек, семья (да и любой социальный институт), биосфера, химические вещества и пр. Системность присутствует даже в неявных вещах.
Очень давно, благодаря энтузиазму моего деда, я научился играть в шахматы. Вообще, шахматы — это одна из самых древних синтетических системных моделей, представленных в оболочке настольной игры. В данной статье будет произведен системный анализ шахмат, как детерминированной (предопределенной) системы, а именно: исследование структуры связанных шахматных фигур, интегративного свойства всех фигур и отдельных «изолированных» структур и уровня доминирования на доске как отдельных фигур, так и отдельного цвета (белых или черных).
Немного о системологии
Дабы не отправлять восприятие неподготовленного читателя в «нокаут», я разберу основные принципы и понятия системологии, которые будут использованы ниже.
- Где структура, там система. Третьего не дано. Один из самых главных принципов теории систем: «Если как минимум два элемента образуют некую взаимосвязь друг с другом, то таким образом порождается прообраз будущей системы». Связь — это фактор появления системности, а структура — это совокупность этих связей и элементов. Здесь важно отметить, что элементом выступает предельно-деленная сущность актуальной реальности, то есть — дальше делить этот элемент либо невозможно, либо бессмысленно.
- Неделимость элементов. Примером вышеописанного элемента в материальном мире выступает любая элементарная частица: лептон, электрон, фотон, гравитон и т.д. В мире социума — человек. Конечно, мы в силах представить человека, как органическую систему, мысленно разобрав его на органы, нервную систему и прочие его составляющие, но в категориях социального мира подобное абсурдно, ибо человек уже является структурной единицей системы. Элементы системы — это структурные единицы любой системы, которая, кстати говоря, также может состоять из множества других под-систем.
- Структурная сложность системы (под- и над-системность). Раз уж мы взяли человека, как пример многоуровневой системы, то давайте рассмотрим его сложность на относительно простой иллюстрации:
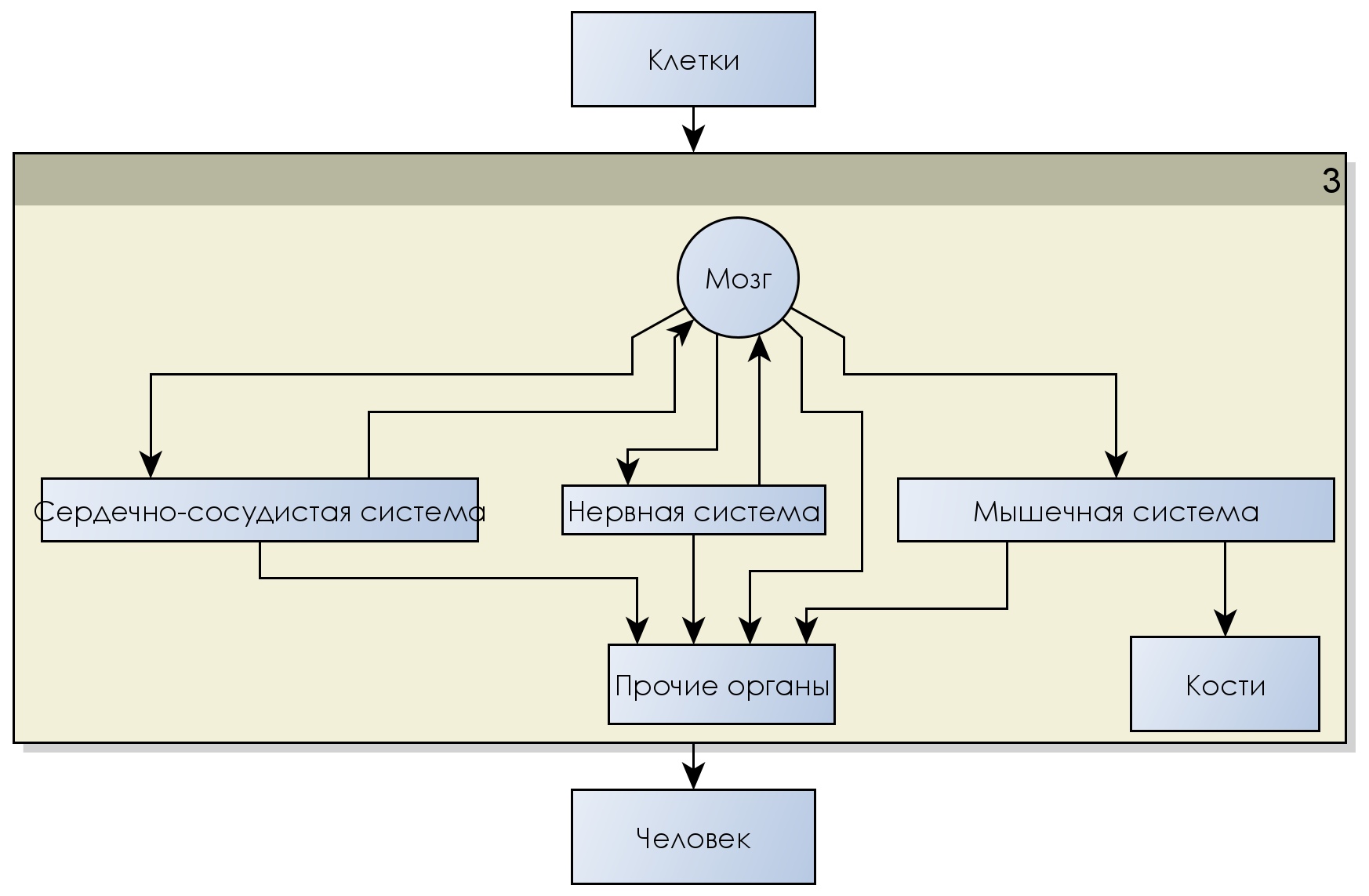
Отчетливо видно, что человеческий организм, который является системой, также содержит в себе огромное количество под-систем, которые можно детализировать до предела клеток, которые есть единицы живых структур (как элементарные частицы и пр.). Конечно, все эти системы связаны и обмениваются различными материями: импульсами и различной энергией (тепловой, кинетической, органической и пр.).
- Интегративное свойствопараметр или эмерджентность. Хорошо. Мы поняли, что между элементами есть связи, что вместо них могут выступать целые системы с системами внутри, что если сущность мы называем элементом, то навешиваем на него ярлык дальнейшей структурной неделимости. Но, самое главное свойство, которое присуще системам — это интегративное свойство, которое является суммой всей деятельности и свойств ее элементов, но не может принадлежать простому элементу. Примеры: «Книга — это в некоторой степени общее свойство всех связанных смыслом страниц, но не принадлежащее страницам по отдельности»; «Физическая сила — совокупность качеств отдельных систем человеческого организма».
Это далеко не все что изучает системология, но остальные принципы будут объясняться по ходу чтения..
Связанные фигуры
В шахматах, при построении любой стратегии необходимо включать в учет в крепкую структуру фигур. Связанная фигурой является защищающей фигурой, поменяв позицию которой (возможно) нарушиться структура. Тут говорить смысла нет, нужно смотреть.

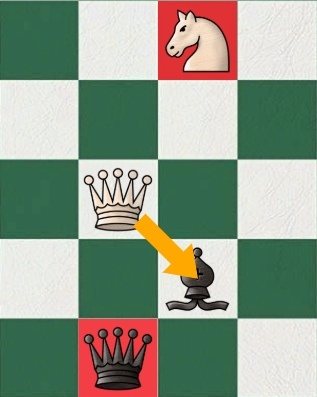
Стрелкой показывается текущий ход.Подсвеченная красным пешка является связанной фигурой, так как защищает пешку выше, от атакующей.
Взглянув на расстановку системно мы можем увидеть два объекта. Первый из них — это правая белая пешка, которая является обособленной и не относящейся ко второму объекту. Второй объект — система. Здесь, давайте подробнее. Внутри системы мы имеем базовую пешечную структуру черных и атакующую эту структуру -пешку белых. Рассмотрим связи в этой системе: черная пешка, подсвеченная красным защищает союзническую пешку выше (связь защиты), а белая пешка нападает на защищаемую пешку (связь нападения). Очевидно, что все шахматные фигуры выступают неделимыми элементами, имеющими различные параметры дальности атаки и хода.
Насколько сложна вся расстановка можно увидеть на диаграмме ниже.
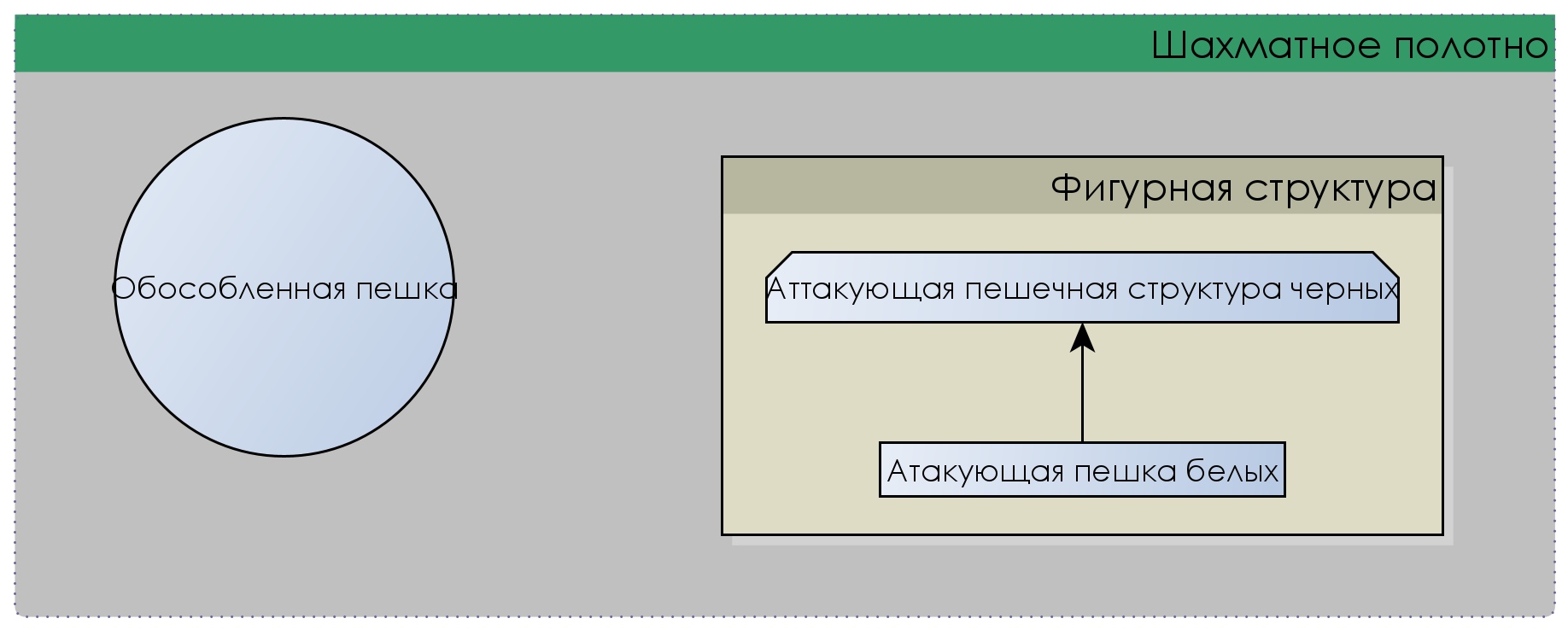
Шахматное полотно выступает над-системой, параметр количества полей которой неограничен (не путать с шахматной доской, ибо она имеет ограниченное количество полей)
Вот еще несколько возможных расстановок, на которых вы можете потренировать системный анализ связанных фигур.

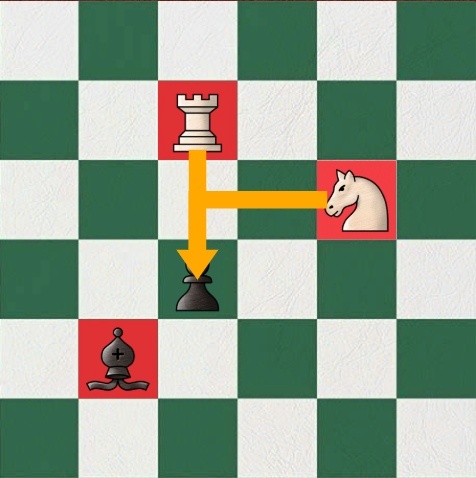
Интегративные параметры
Говорить об интегративных свойствах и параметрах фигурных структур нужно при большом количестве элементов (не забывайте, что мы принимаем фигуры за предельно делимые объекты). В своих наблюдениях я вывел три интегративных параметра в шахматах: параметр охвата территории, параметр атаки и параметр связности.
Интегративный параметр охвата территории. Это суммарный количественный показатель потенциальных полей для атаки и перехода. В начале партии данные параметры обоих систем равны 8 (нацеливание пешек и коней). Важно отметить, что каждое потенциальное поле идет за 1, то есть количество нацеленных фигур на одинаковое поле не имеет значения (на иллюстрации ниже эти поля выделены зеленым). Система фигур с большим параметром охвата территории имеет большее преимущество перед другими системами.

Интегративный параметр атаки. Это модификация вышеописанного параметра. Различие только в учете уникальных атакующих фигур. В начале партии эти параметры атаки систем равны 16 (на иллюстрации ниже зелёным отмечены поля с коэффициентом 1; синим — 2; красным — 3).

Интегративный параметр связности. Думаю, что из названия очевидно, что это количественный показатель связных структур. Подсчет этого параметра происходит последовательно. Допустим, имеем следующую расстановку:
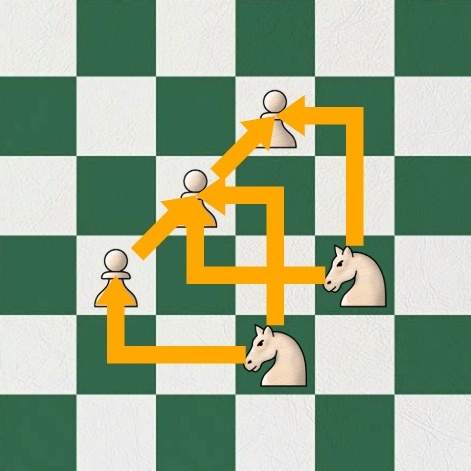
Стрелкой показаны связи защиты, подсчитав которые мы и получим параметр связности (в данном случае он равняется 6).
Заключение
Это не все. На самом деле для практики основ системного подхода шахматы просто идеальная модель — она умеренно абстрактна, обладает глубокой стратегией и неоднородностью элементов. Также, если вы уже неплохо продвинулись в изучении системологии и системном анализе рекомендую переключиться с шахмат на Го, которая обладает в десятки раз глубокой стратегией чем шахматы.
Список используемой литературы
Огнев, А.О. Основы системологии: учеб. пособие / А.О. Огнев. – 2-е изд. –
Тольятти: ТГУ, 2008. – 254 с.
Автор: Михаил Плясунов






