Что такое процедурная генерация?
Процедурная генерация включает в себя множество генеративных алгоритмов, принцип работы которых заключается в создании данных не вручную, а алгоритмически: вместо ручного изготовления того, что мы хотим создать (карты, музыки, рельефа…), пишется алгоритм, который успешно может создавать различные примеры без многократного выполнения того же процесса. Особенно полезен такой подход в видеоиграх, где случайным образом может генерироваться целая карта или уровень (например, карты в Minecraft, Terraria или Factorio, или схемы уровней в большинстве roguelike).
Алгоритм коллапса волновой функции и его области применения
В статье мы исследуем алгоритм коллапса волновой функции (WaveFunctionCollapse, WFC), предложенный Максимом Гуминым (в его Twitter есть коллекция потрясающего контента, созданного при помощи этого алгоритма другими разработчиками!) для процедурной генерации изображений или рельефа при помощи создания изображений, локально схожих с входящим изображением в условиях сетки заданного размера.
В основе алгоритма лежит идея пошагового создания готового изображения с отслеживанием того, какие тайлы «соответствуют» уже частично построенному изображению. Для изучения подробного описания алгоритма рекомендуем обратиться к исходному репозиторию WFC на Github и четвёртому разделу статьи "WaveFunctionCollapse is Constraint Solving in the Wild".
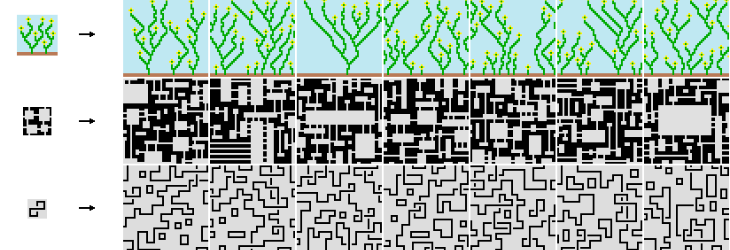
Примеры процедурно сгенерированных из seed изображений
Кроме создания схожих изображений ещё одной областью применения алгоритма WFC является генерация тайловых карт. Генерация тайловых карт будет основной темой статьи, потому что её проще использовать для наглядного объяснения наших идей. Вместо примера изображения можно хранить только тайлы и пары тайлов, которые могут соединяться друг с другом с поворотами. При этом алгоритм можно использовать для создания изображений, похожих на показанное ниже.

Примеры сгенерированного случайным образом рельефа на основе тайлов
Задача и наше решение
Мы занялись задачей генерации тайловой карты на основании настольной игры Carcassonne («Каркассон»), в которой поле генерируется игроками «вручную» (см. анимацию ниже) из тайлов, которые должны сочетаться друг с другом.
Как ни удивительно, концептуально это очень похоже на работу алгоритма WFC по созданию произвольных тайловых карт добавлением новых частей к неполному решению. И поскольку WaveFunctionCollapse можно использовать в качестве генератора тайловых карт, с его помощью можно генерировать и поля «Каркассона»!
Однако в самой игре слишком много разных тайлов, и кодирование всех их соотношений — чересчур объёмная задача для 24-часового хакатона. Поэтому мы решили играть очень упрощённой версией «Каркассона» без замков и рек, только с дорогами, травой и монастырями. Так мы получили 6 возможных тайлов с их поворотами и симметрией. Но даже при таких условиях результат выглядит красиво и походит на реальную игру в «Каркассон»!
Визуализация заполнения алгоритмом поля «Каркассона»

Пример введённых в алгоритм правил
На изображении сверху содержится пример входных правил, добавляемых в алгоритм. Однако нам всё равно нужно контролировать отдельные аспекты внешнего вида поля. Должен ли алгоритм создавать «улицы» из дорог, заполненные монастырями и похожие на город, или поле по большей мере должно состоять из травы с разбросанными по ней деревнями? В исходном алгоритме нет никакой возможности контролировать подобные условия (как и любые другие), но для возможности управления в него можно внести простое улучшение.
Байесовское априорное распределение вероятностей
Как сказано выше, на каждом шаге алгоритм добавляет к полю новый тайл таким образом, чтобы он соответствовал уже размещённым тайлам, но мы не говорили, что произойдёт, если в выбранное место можно поместить несколько разных тайлов (мы также не говорили и о том, как вообще выбирать это место, но в статье мы это рассматривать не будем!). В исходном алгоритме любой подходящий тайл выбирается равномерным случайным образом. Однако в своём решении мы можем предпочитать конкретные тайлы, например, траву, чтобы она встречалась на поле чаще. Это можно реализовать, создав неравномерное «априорное распределение вероятностей» («probability prior») тайлов, при котором трава имеет бОльший шанс на использование, чем дорога, в случае, если можно использовать оба типа тайла. Это напоминает байесовские техники. В упрощённом случае выбора между двумя вариантами, травой и дорогами, мы можем добавлять траву с вероятностью p > 0.5, а не с обычной 0.5, получаемой при равномерной вероятности. Эту задачу легко обобщить, назначив каждому тайлу «значение приоритета» и использовав это значение для задания вероятности как значения, разделенного на сумму значений всех возможных тайлов. На рисунке ниже показаны два подходящих решения с сильно отличающимися значениями коэффициентов, дающие понимание того, насколько чувствительным может быть алгоритм.

Различные решения при разных исходных априорных распределениях вероятностей
Ещё один пример: условные вероятности и группирование
Можно расширить эту идею, и чтобы проиллюстрировать это, мы сгенерируем вместо полей «Каркассона» двухмерные карты руды Minecraft. Разные виды руды в Minecraft обычно встречаются крупными формациями, поэтому наряду с заданием вероятности каждой руды мы сделаем так, чтобы вероятности зависели от уже размещённых на карте соседей. Даже несмотря на то, что в расположении железа рядом с углём нет ничего «запрещённого», рядом с уже размещённым углём больший приоритет отдаётся ещё одному углю.
Хотя на изображении ниже это не учитывается, в игре вероятность также зависит от высоты тайлов, поэтому позиция на изображении тоже может влиять на условия распределения вероятностей тайлов.

Пример тайловой карты руды Minecraft, созданный алгоритмом WFC
Заключение
Процедурная генерация — мощный инструмент, который стоит иметь в запасе. В частности, в генерации миров активно используется WFC, и стоит рассмотреть возможность того, что распределение новых тайлов может быть неравномерным и на него могут влиять другие факторы, например, уже размещённые на карте соседи, новые тайлы и позиция на изображении. Мы создали очень простое приложение, но возможности для развития почти безграничны!
Автор: PatientZero






