Привет, Хаброжители! Цель этой книги — познакомить с квантовыми вычислениями всех, кто знаком с курсом математики средней школы и готов немного потрудиться. В этой книге мы будем знакомиться с кубитами, запутанностью (квантовых состояний), квантовой телепортацией и квантовыми алгоритмами, а также с другими темами, имеющими отношение к квантовым компьютерам. Задача состоит не в том, чтобы дать смутное представление об этих понятиях, а в том, чтобы сделать их кристально ясными.
Квантовые вычисления часто упоминаются в новостях: Китай телепортировал кубит с Земли на спутник; алгоритм Шора поставил под угрозу ныне используемые методы шифрования; квантовое распределение ключей снова сделает шифрование надежным средством защиты; алгоритм Гровера увеличит скорость поиска данных. Но что все это означает в действительности? Как все это работает? Об этом Крис Бернхард и собирается рассказать.
Отрывок. Эйнштейн и локальный реализм
Хорошим примером для объяснения локального реализма может служить гравитация. Закон тяготения Ньютона дает формулу силы притяжения между двумя массами. Если подставить в нее размеры масс, расстояние между ними и гравитационную постоянную, можно получить величину силы притяжения. Закон Ньютона изменил физику. С его помощью, например, можно доказать, что планета вращается вокруг звезды по эллиптической орбите. Однако несмотря на то, что закон описывает величину силы, он ничего не говорит нам о природе этой силы.
Закон тяготения Ньютона можно использовать для расчетов, но он не объясняет, как работает гравитация. Сам Ньютон тоже был этим обеспокоен. Все думали, что должна быть какая-то более глубокая теория, объясняющая действие гравитации. Делалось множество разных предположений, часто с привлечением «эфира», который должен быть неотъемлемой частью Вселенной. И хотя не было единого мнения о механизме работы гравитации, никто не считал гравитацию сверхъестественным действием на расстоянии, и все верили, что можно найти какое-то естественное объяснение. Была вера в то, что сейчас мы называем локальным реализмом.
На смену закону тяготения Ньютона пришла теория гравитации Эйнштейна. Она не только усовершенствовала теорию Ньютона с точки зрения точности предсказания астрономических наблюдений, которые нельзя вывести с помощью теории Ньютона, но также объяснила, как работает гравитация. Она описала искажение пространства-времени. Согласно ей, планета движется в соответствии с формой пространства-времени, в котором она находится. Никаких сверхъестественных действий на расстоянии. Теория Эйнштейна была не только более точной, но также описала, как работает гравитация, и это описание было локальным. Планета движется в соответствии с формой пространства в ее окрестностях.
Копенгагенская интерпретация в квантовой механике повторно ввела идею о сверхъестественном действии на расстоянии. При измерении пары запутанных кубитов их состояние изменяется немедленно, даже если они физически удалены друг от друга. Рассуждения Эйнштейна кажутся вполне естественными. Он только что исключил сверхъестественное действие из теории гравитации и теперь снова столкнулся с ним. В отличие от него, Бор не верил в существование более глубокой теории, способной объяснить механизм этого действия. Эйнштейн был не согласен с ним.
Эйнштейн верил, что сможет доказать ошибочность позиции Бора. В соавторстве с Борисом Подольским (Boris Podolsky) и Натаном Розеном (Nathan Rosen) он написал статью, в которой указывал, что его специальная теория относительности подразумевает невозможность распространения информации быстрее скорости света, но мгновенные действия на расстоянии означают, что информация от Алисы к Бобу может доставляться мгновенно. Эта проблема получила название ЭПР-парадокс, то есть парадокс Эйнштейна—Подольского—Розена.
В наше время ЭПР-парадокс обычно описывается с позиции спина, и именно так мы и сделаем, хотя Эйнштейн с соавторами описывал проблему иначе. Они рассматривали местоположение и импульс двух запутанных частиц. А формулировку с позиции спина предложил Дэвид Бом (David Bohm). Именно формулировка Бома используется в настоящее время, и именно ее использовал Джон Сюарт Белл для вычисления своего важного неравенства. Несмотря на то что Бом сыграл важную роль в описании и формулировании парадокса, его имя обычно опускается.
В предыдущей главе указывалось, что копенгагенская интерпретация не допускает возможности передачи информации быстрее скорости света, и поэтому, хотя ЭПР-парадокс на самом деле не является парадоксом, все еще стоит вопрос о наличии объяснения, устраняющего сверхъестественность действия.
Эйнштейн и скрытые переменные
С классической точки зрения физика является детерминированной — если начальные условия известны с бесконечной точностью, можно предсказать точный результат. Конечно, начальные условия могут быть известны только с некоторой конечной точностью, в том смысле, что измерения всегда имеют некоторую погрешность — небольшую разность между измеренным и истинным значением. С течением времени эта ошибка может увеличиваться до значения, которое уже не позволит получить адекватный прогноз. Эта идея лежит в основе так называемой чувствительной зависимости от начальных условий. Она объясняет, почему прогноз погоды дальше чем на неделю крайне ненадежен. Однако важно помнить, что основополагающая теория детерминирована. Погода выглядит непредсказуемой, но это не связано с какой-то присущей ей случайностью, просто мы не можем выполнить измерения с достаточно высокой точностью.
Другая область, где вероятность вторгается в классическую физику, — законы, касающиеся газов, то есть законы термодинамики, но сама теория снова является детерминированной. Если точно знать скорость и массу каждой молекулы в газе, теоретически можно точно предсказать, что произойдет с каждой молекулой в будущем. На практике же молекул оказывается слишком много, чтобы можно было учесть каждую из них, поэтому мы берем средние значения и рассматриваем газ со статистической точки зрения.
Именно на этот классический детерминистский взгляд ссылался Эйнштейн, когда очень здорово высказался, что Бог не играет в кости со Вселенной. Он чувствовал, что использование вероятности в квантовой механике демонстрирует неполноту теории. Должна существовать более глубокая теория, возможно, включающая новые переменные, которая является детерминированной, но выглядит вероятностной, если не принимать во внимание все эти пока неизвестные переменные. Эти неизвестные переменные стали называть скрытыми переменными.
Классическое объяснение запутанности
Начнем с наших квантовых часов, находящихся в состоянии
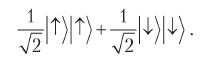
Алиса и Боб задают вопрос: указывает ли стрелка на двенадцать? Квантовая модель утверждает, что они оба получат один и тот же ответ: «да, стрелка указывает на двенадцать» или «нет, стрелка указывает на шесть». Оба ответа равновероятны. На самом деле мы можем провести эксперименты со спинами запутанных электронов. Результаты этих экспериментов будут в точности соответствовать тому, что предсказывает квантовая модель. Но как эти результаты объясняет классическая модель?
Классическая интерпретация описанной ситуации выглядит довольно просто. Электроны имеют определенный спин в любом направлении. Запутанные электроны запутываются в результате некоторого локального воздействия. И снова мы обращаемся к скрытым переменным и более глубокой теории. Мы не знаем точно, что происходит, но есть некоторый локальный процесс, который переводит электроны в одно и то же состояние спина. Когда они запутаны, направление спина выбирается сразу для обоих электронов.
Это можно сравнить с ситуацией, когда у нас есть колода карт, которую мы сначала перемешиваем, затем не глядя извлекаем одну карту, разрезаем ее на две половины и вкладываем в два конверта, все это время не зная, какая карта была извлечена из колоды. Затем мы посылаем конверты Бобу и Алисе, живущим в противоположных концах Вселенной. Ни Алиса, ни Боб не подозревают, какую карту они получили. Это может быть любая карта из пятидесяти двух, но как только Алиса вскроет свой конверт и увидит бубнового валета, она будет точно знать, что Боб тоже получил половинку карты бубнового валета. Нет никакого действия на расстоянии и ничего сверхъестественного.
Чтобы прийти к результатам, полученным Беллом, мы должны измерить наши запутанные кубиты в трех разных направлениях. Теперь вернемся к аналогии запутанных часов и будем задавать три вопроса: указывает ли стрелка на двенадцать, на четыре и на восемь. Теоретическая квантовая модель утверждает, что на каждый вопрос будет получен ответ либо «да, указывает», либо «нет, она указывает в противоположном направлении». Оба ответа на каждый вопрос равновероятны. Но когда Алиса и Боб зададут один и тот же вопрос, они получат один и тот же ответ. Описать это с классической точки зрения можно точно так же, как и раньше.
Существует некоторый локальный процесс, который запутывает часы. Мы не пытаемся описать, как именно это делается, а просто ссылаемся на скрытые переменные — есть какая-то более глубокая теория, которая объясняет все это. Но когда часы запутаны, на три вопроса выбираются вполне определенные ответы. Это можно сравнить с ситуацией, когда имеется три колоды карт с рубашками разного цвета. Мы извлекаем по одной карте из колоды с синей, красной и зеленой рубашкой. Разрезаем каждую пополам и посылаем три половинки Алисе и три половинки Бобу. Если Алиса увидит половинку карты бубнового валета с зеленой рубашкой, она будет точно знать, что Боб получит половинку карты с зеленой рубашкой, которая является бубновым валетом.
В отношении наших квантовых часов классическая теория гласит, что на каждый вопрос имеется определенный ответ, который предопределен еще до того, как будет задан вопрос. Квантовая теория, напротив, гласит, что ответ на вопрос не определен, пока он не задан.
Неравенство Белла
Представьте, что мы сгенерировали поток пар кубитов и послали их Алисе и Бобу. Каждая пара кубитов находится в запутанном состоянии
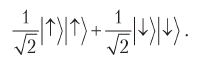
Алиса случайным образом выбирает направление 0°, 120° или 240° для измерения своего кубита. Каждое из этих направлений выбирается случайно, с вероятностью 1/3. Алиса не запоминает выбираемые направления, но записывает получаемый результат, 0 или 1. (Напомню, что 0 соответствует первому базисному вектору, а 1 — второму.) После того как Алиса измерит свой кубит, Боб случайно, с вероятностью 1/3, выбирает одно из тех же трех направлений и измеряет свой кубит. Так же как Алиса, он не запоминает направление измерения, но записывает полученный результат, 0 или 1.
В итоге Алиса и Боб получают по длинной строке из 0 и 1. Затем они сравнивают свои строки, символ за символом. Если первые символы совпадают, они записывают букву A, если не совпадают — букву D. Затем переходят ко второму символу и также записывают A или D, в зависимости от совпадения или несовпадения. Так они сравнивают все символы в своих строках.
В результате получается новая строка, состоящая из букв A и D. Какая доля строки придется на символ A? Белл заметил, что модель квантовой механики и классическая модель дают разные ответы.
Ответ модели квантовой механики
Кубиты находятся в запутанном состоянии
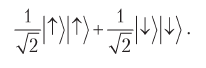
Мы уже видели, что если Алиса и Боб оба выберут одно и то же направление для измерения, они получат один и тот же ответ. Теперь посмотрим, что случится, если они выберут разные базисы.
Начнем со случая, когда Алиса выбирает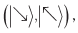 
а Боб выбирает 
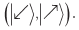Запутанное состояние
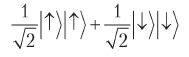
можно записать, используя базис Алисы, как
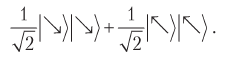
Когда Алиса выполняет свое измерение, происходит переход в состояние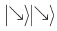 
или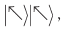 
каждое из которых равновероятно. Если произошел переход в состояние 
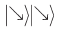, она запишет 0. Если произошел переход в состояние 
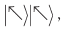она запишет 1.
Теперь измерение должен выполнить Боб. Допустим, что после измерения Алисой кубиты находятся в состоянии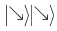 
то есть кубит Боба находится в состоянии 
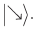Чтобы вычислить результат измерения Бобом, нужно переписать это состояние, использовав базис Боба. (Похожие вычисления мы уже делали в разделе «Алиса, Боб и Ева» главы 3.)
Записав решение с использованием двумерных кетов, получаем:
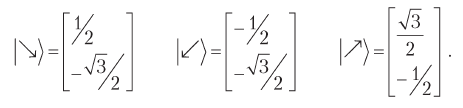
Умножим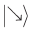 
на матрицу со строками, соответствующими бра из базиса Боба.
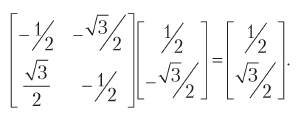
В результате получаем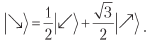 
Выполнив измерение, Боб получит 0 с вероятностью 1/4 и 1 с вероятностью 3/4. То есть когда Алиса получит 0, Боб получит 0 с вероятностью 1/4. Легко проверить другой случай. Если Алиса получит 1, Боб также получит 1 с вероятностью 1/4.
Другие случаи дают аналогичные результаты: если Боб и Алиса производят измерения в разных направлениях, их результаты совпадут в 1/4 случаев и не совпадут в 3/4 случаев.
В итоге в 1/3 случаев они выполняют измерения в одном направлении и всегда получают совпадения; в 2/3 случаев они выполняют измерения в разных направлениях и получают совпадения в 1/4 случаев. Соответственно, доля символов A в строке из A и D составляет
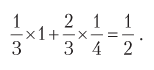
Таким образом, согласно модели квантовой механики, при достаточно большом числе испытаний доля символов A должна составлять половину.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Квантовые вычисления
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Автор: ph_piter
