Все, что вы хотели знать об обратном маятнике

в 19:02, , рубрики: Алгоритмы, обратный маятник, программирование микроконтроллеров, Разработка под Arduino, Разработка робототехники, Электроника для начинающих

Статья служит шпаргалкой для тех, кто хочет сделать свой обратный маятник. Здесь описаны проблемы, из-за которых я все переделывал несколько раз, приведен краткий обзор теории, необходимый для понимания, как стабилизировать систему.

Зачем мне это было нужно?

Коротко: хотел расширить свой ЧПУ станок, но что-то пошло не так…

Полная версия истории
Еще с детства хотелось иметь свой ЧПУ станок, т.к. занимался моделями самолетов, где нужно делать много маленьких повторяющихся деталей. Сначала купил готовый DIY наборчик, а потом решил увеличить. Поигрался два месяца, но все же станок маленький, рабочая область была лишь 18 на 10 см, в нем нет сенсоров позиционирования. Решил купить направляющую побольше, поставить концевые выключатели и установить каретку в середину шаговым мотором. Сделал за пол дня, но нельзя же по прямой к мечте идти — к большому ЧПУ, надо усложнить задачу и поставить маятник на каретку, тогда мне это показалось просто, но пришлось вспомнить институтские годы и ознакомиться с ТАУ.

Неудачные попытки

Проект занял почти два года проб и ошибок, перепроектирования, ожидания деталей и неполно прожитых выходных, чтобы желающие повторить сэкономили себе время и нервы, считаю нужным рассказать о неудачных решениях.

  • гироскоп (MPU6050) вместо энкодера — принципиально ничего против, но датчик должен располагаться на вращающемся стержне, это вносит непредсказуемое воздействие и невозможность прокрутить стержень несколько раз вокруг оси.
  • абсолютный энкодер — если это потенциометр, то шум в измерения вносит даже движение проводов (в основном из-за контактов в arduino), 10-ти битный АЦП — это все же мало; если это более дорогой датчик, то считывание происходит по последовательному интерфейсу, а это вносит задержку в систему особенно в совокупности с шаговым мотором.
  • нежесткость системы — в какой-то момент я брал алюминиевую трубку с грузом на конце, при колебаниях каретки, в ней самой начинались сильные колебания, и тут же было непонятно какую систему мы стабилизуем. Надо стремиться к тому, чтобы физическая система была максимально приближена тому, что смоделировано.
  • трение — этим явлением часто пренебрегают, я старался уменьшить его, используя большие колеса каретки и V-slot профили, в отличие от рельсов с ползунками с маленькими шариками, т.к. трение качения обратно пропорционально радиусу.
  • использование шагового двигателя — много времени потратил, пытаясь пойти этим путем, вводит в заблуждение упрощение формул (фактически мы сразу управляем ускорением основания маятника) и простота конструкции (можно забыть про трение в рельсе, энкодер мотора, если предположить, что шаги мотор не пропускает), но… Чтобы точно управлять скоростью, время между шагами должно исчисляться десятками микросекунд, значит о выводе состояния в консоль можно забыть. Без обратной связи нельзя быть уверенным, что мотор не пропустил шаги и скорость действительно такая, как система думает. Не утверждаю, что это тупиковое решение, если кому-то удастся стабилизировать маятник шаговым мотором, буду рад на это взглянуть.

Свободный маятник

Для полноты картины, смоделируем маятник на свободной каретке без трения.
Все, что вы хотели знать об обратном маятнике - 1
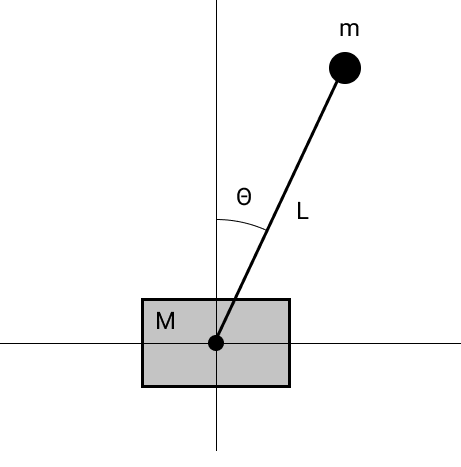
Уравнения движения можно получить дифференцированием лагранжиана по обобщенным координатам. Получим следующие уравнения:

$ begin{cases} Lcdotddottheta + gcdot{sin(theta)} - ddot{x}cdot{cos(th)}=0 \ (m + M)cdotddot{x} + mcdotddot{theta}cdot{L}cdot{cos(theta)} - mcdot{L}dot{theta}^2cdot{sin(theta)}=0 end{cases} $

из которых можно найти, как меняется вектор состояния:

$ begin{cases} dottheta=w\ dot{w}=frac{g cdot{sin(theta)} + bcdot{L}cdot{w^2}cdot{sin(theta)}cdot{cos(theta)}}{Lcdot(1 + bcdot{cos^2(theta))}}\ dot{x}=v\ dot{v}=bcdotfrac{Lcdot{w^2}cdot{sin(theta)} - gcdot{sin(theta)}cdot{cos(theta)}}{1 + bcdot{cos^2(theta)}} end{cases} , b=frac{m}{M + m} $

и смоделировать систему. Код здесь.
Все, что вы хотели знать об обратном маятнике - 4

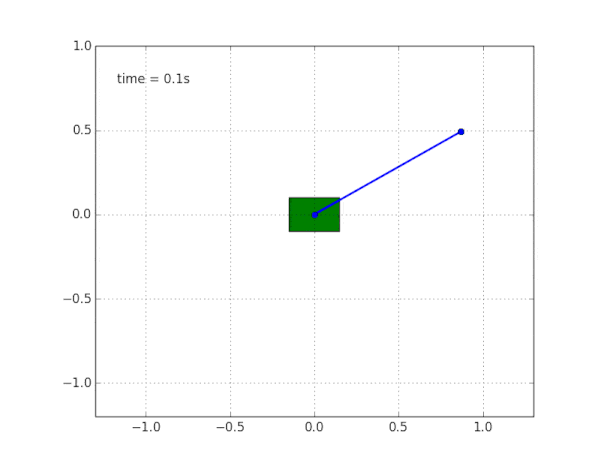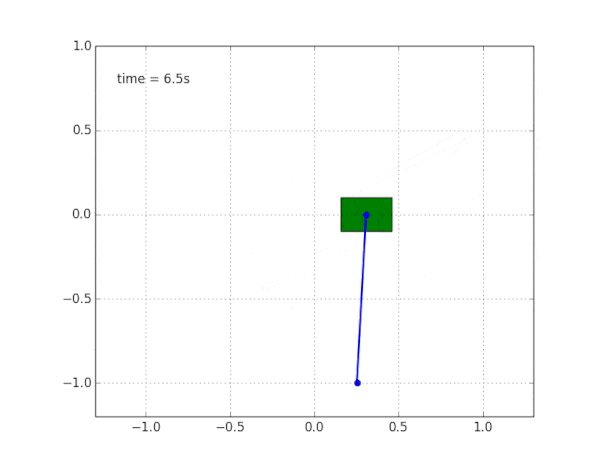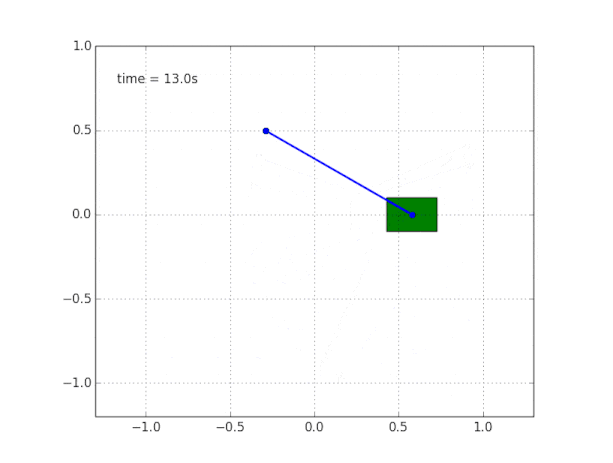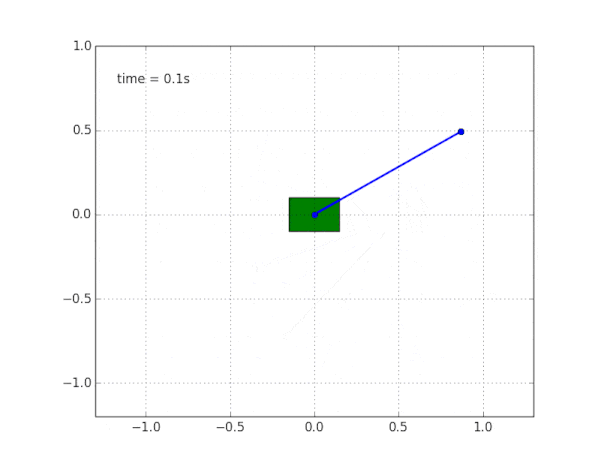
Почему система неустойчива?

Здравый смысл и визуализация нам подсказывают, что маятник сам по себе стоять не будет. Но как в этом убедиться математически?
В общем виде линеаризованная система и решение выглядят следующим образом:

$ dot{mathbf{x}}=Amathbf{x}, mathbf{x}(t)=e^{At}mathbf{x}(0) $

Экспонента в степени матрицы выглядит понятней, если перейти в систему координат из собственных векторов, тогда матрица $А$ будет диагональной($D$), и экспонента будет иметь вид:

$ e^{Dt}=begin{bmatrix} e^{lambda_1t} & 0 & dots & 0 \ 0 & e^{lambda_2t} & dots & 0 \ vdots & vdots & ddots & vdots \ 0 & 0 & dots & e^{lambda_nt} \ end{bmatrix} $

Теперь видно, при наличии собственных значений ($lambda_i$) с положительной действительной частью, соответствующая компонента вектора состояния будет стремиться в бесконечность, и система развалится. Вышесказанное касается непрерывных систем, более подробно про устойчивость рассказывается в этой видео-лекции.
Проверим так ли это, для обратного маятника. Линеаризуем нашу систему около положения равновесия при $theta=0, sin(theta) approx theta, cos(theta) approx 1, w^2 approx 0$:

$ begin{bmatrix} dottheta \ dotomega\ dot{x} \ dot{v} end{bmatrix}=begin{bmatrix} 0 & 1 & 0 & 0 \ frac{g}{L(1 + b)}{theta} & 0 & 0 & 0 \ 0 & 0 & 0 & 1 \ -gfrac{b}{1 + b}theta & 0 & 0 & 0 end{bmatrix} begin{bmatrix} theta \ omega\ x \ v end{bmatrix} $

Ненулевые собственные значения имеют вид $pmsqrt{frac{g}{L(1 + b)}}$, таким образом мы убедились в неустойчивости.

Добавляем обратную связь

Теперь на каретку будет действовать сила $f$, одно из уравнений перепишется в виде: $(m + M)cdotddot{x} + mcdotddot{theta}cdot{L}cdot{cos(theta)} - mcdot{L}dot{theta}^2cdot{sin(theta)}=f$, и линеаризованная система примет вид:

$ begin{bmatrix} dottheta \ dotomega\ dot{x} \ dot{v} end{bmatrix}=begin{bmatrix} 0 & 1 & 0 & 0 \ frac{g}{L(1 + b)}{theta} & 0 & 0 & 0 \ 0 & 0 & 0 & 1 \ -gfrac{b}{1 + b}theta & 0 & 0 & 0 end{bmatrix} begin{bmatrix} theta \ omega\ x \ v end{bmatrix} + begin{bmatrix} 0 \ frac{1}{L}frac{1}{2m + M} \ 0 \ frac{1}{2m + M} end{bmatrix} cdot{f} $

Теперь система ($dot{mathbf{x}}=Amathbf{x} + Bu$) стала управляемой, в этом можно убедиться, проверив, что ранг матрицы $begin{bmatrix} B && AB && A^2B && A^3B end{bmatrix}$ равен размерности вектора состояния, т.е. 4. Для удержания маятника в вертикальном положении я использовал линейно-квадратичный регулятор состояния, т.е. управление (u или f) есть произведение вектора состояния $[theta, dot{theta}, x, dot{x}]$ на вектор параметров, которые находятся один раз минимизацией квадратичного функционала. Код симуляции здесь.
Все, что вы хотели знать об обратном маятнике - 19

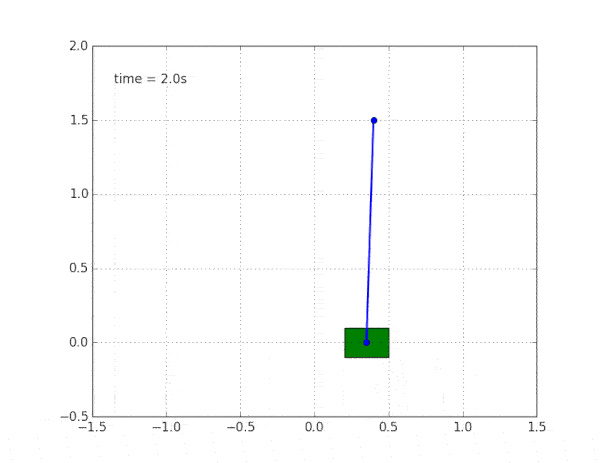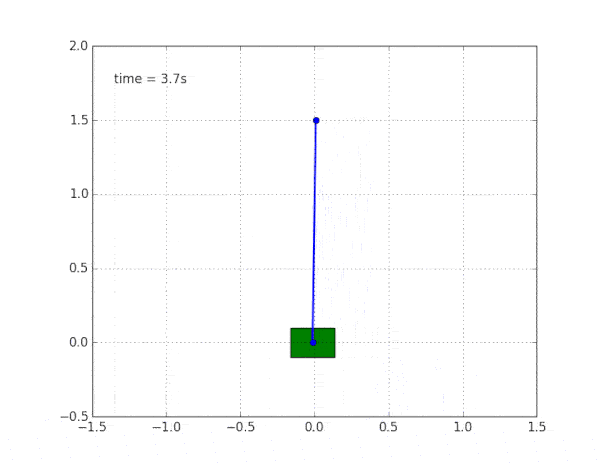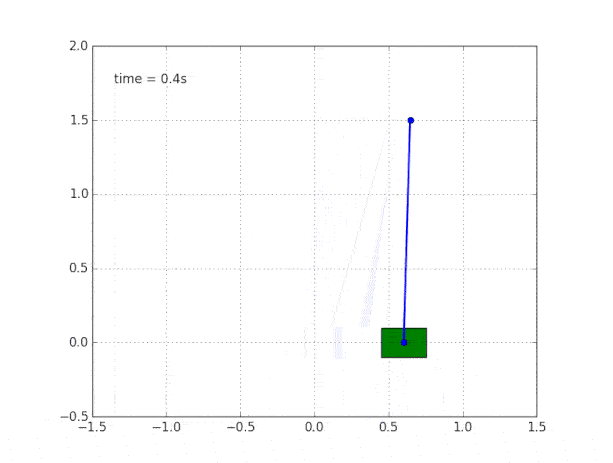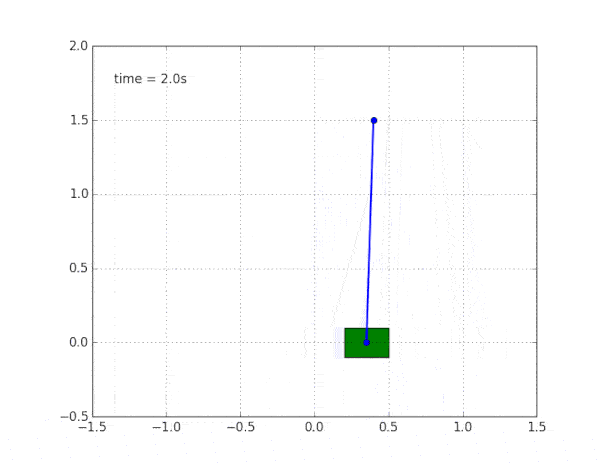
Управление двигателем

Теперь нужно управлять мотором постоянного тока, он содержит много параметров, которых я не знаю, поэтому я принял его за «черный ящик», описываемый следующими уравнениями с учетом трения:

$ begin{cases} dot{x}=v \ dot{v}=-acdot{v} + bcdot{U} + ccdot{sign(v)} end{cases} $

Про вывод уравнений и оценку параметров можно прочитать здесь. Ниже приведу мои графики разгона мотора с кареткой в зависимости от напряжения (в реальности на выходе контроллера ШИМ-сигнал) и подогнанные кривые.
Все, что вы хотели знать об обратном маятнике - 21
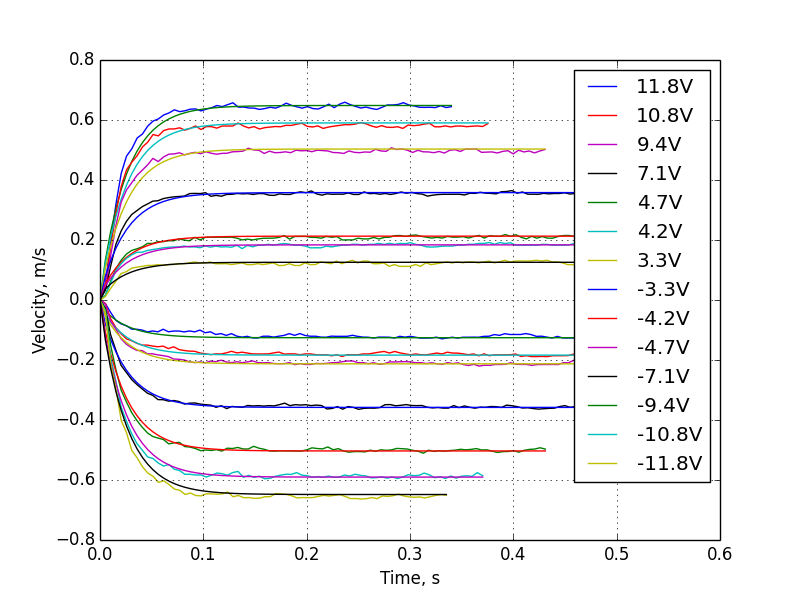
Коэффициенты модели я также нашел перебором, код.
Таким образом, регулятор дает нам требуемое ускорение, а из 2-го уравнения, зная все константы, найдем напряжение.

Собираем реальное устройство

Теперь у нас есть все знания, чтобы собрать и стабилизировать маятник. Я использовал следующее железо:

  • Arduino Mega 2560 — не UNO, потому что для двух энкодеров нужно 4 пина для прерываний
  • Энкодер для маятника — OMRON E6B2-CWZ6C 2500 пульсов на оборот — дает нам угол, вычисляем угловую скорость, разрешение достаточно высокое, поэтому хватило конечных разностей без сглаживания и усреднения
  • Энкодер для мотора — LPD3806-600BM-G5-24C 600 пульсов на оборот — дает положение каретки, вычисляем скорость
  • DC-мотор на 12V с редуктором 5:1
  • Драйвер мотора 10Amp 5V-30V

Таким образом мы явно измеряем угол маятника, положение каретки, вычисляем угловую скорость маятника и скорость каретки — получаем полное состояние, параметры регулятора я нашел этим скриптом. К удивлению все достаточно быстро заработало как есть. Результатом я доволен, стоит и даже стакан держит!

Код для Arduino находится здесь
Что удалось усовершенствовать по сравнению с многими вариантами, которые можно найти на youtube — этот маятник тихий, потому что ШИМ настроен вне слухового диапазона, и используются пластиковые колеса.
Теперь эта задача выглядит, как лабораторная работа: измерить параметры мотора и найти коэффициенты регулятора, попутно разбираясь в происходящем.

Что дальше?

Планирую продуктизовать маятник: сделать раскачивание, избавиться от мотка проводов, сделать shield у удобными разъемами, чтобы не стыдно было подарить в какую-нибудь школу или музей. Если кто-то желает присоединиться, буду рад, есть еще много амбициозных идей.

Ссылки

Спасибо за внимание!

Автор: zjor

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js