В рамках своей научной активности реализовал так называемый Федеративный Фильтр Калмана (Federated Kalman Filter). В этой статье рассказывается о том, что такое «Федеративный ФК», чем он отличается от обобщенного, а также описывается консольное приложение, реализующее данный фильтр и генетические алгоритмы для подбора параметров его математической модели. Приложение было реализовано с использованием TPL (Task Parallel Library), поэтому пост будет интересен не только специалистам по цифровой обработке сигналов.
Введение
На хабре уже писали о том, что такое Фильтр Калмана (ФК), для чего он нужен и как он составляется (концептуально). Ниже некоторые из имеющихся статей.
• Фильтр Калмана
• Фильтр Калмана — !cложно?
• Фильтр Калмана — Введение
• На пороге дополненной реальности: к чему готовиться разработчикам (часть 2 из 3)
• Неортогональная БИНС для малых БПЛА
• Классическая механика: о диффурах «на пальцах»
Также, на хабре есть достаточно много статей о применении разных стохастических алгоритмов оптимизации нелинейных функций многих переменных. Сюда я включаю эволюционные алгоритмы, имитацию отжига, популяционный алгоритм. Ссылки на некоторые из статей ниже.
• Метод имитации отжига
• Что такое генетический алгоритм?
• Генетические алгоритмы. От теории к практике
• Генетические алгоритмы, распознавание изображений
• Генетический алгоритм. Просто о сложном
• Генетические алгоритмы для поиска решений и генерации
• Генетический алгоритм на примере бота Robocode
• Генетические алгоритмы в MATLAB
• Популяционный алгоритм, основанный на поведении косяка рыб
• Концепции практического использования генетических алгоритмов
• Обзор методов эволюции нейронных сетей
• ТАУ-Дарвинизм
• Естественные алгоритмы. Алгоритм поведения роя пчёл
• Естественные алгоритмы. Реализация алгоритма поведения роя пчёл
В одной из своих прошлых статей (ТАУ-Дарвинизм: реализация на Ruby) я представлял вашему вниманию результаты использования генетических алгоритмов (ГА) для подбора параметров математической модели динамической системы. В данной статье представлены результаты использования ГА в более сложной задаче – синтезе модели Фильтра Калмана. В рамках этой задачи я «натравил» генетические алгоритмы на параметры динамики в переходной матрице (она же Transition Matrix) ФК. Также ГА можно было использовать и для подбора значений ковариационных матриц в ФК, но я решил пока этого не делать. Шумы я генерировал сам, потому матрица ковариаций ошибок измерений мне была известна заранее. Матрица ковариаций шумов процесса на практике никогда неизвестна точно, потому я выбрал ее значение исходя из максимальной чувствительности ФК к изменению значений в переходной матрице.
Как бы то ни было, расширить описанную тут задачу на случай оптимизации значений матриц ковариаций будет несложно. Просто нужно будет реализовать еще одну целевую функцию, в которой матрицы ковариаций будут генерироваться по значениям генов особи, а значение переходной матрицы будет задаваться заранее. Таким образом получится разделить на два этапа весь процесс синтеза ФК:
1. Оптимизация параметров математической модели ФК
2. Оптимизация значений ковариационных матриц
Второй этап, как я написал выше, у меня не реализован пока. Однако реализация его в планах имеется.
Постановка задачи
Итак, задача. Пусть мы имеем некую измерительную систему, состоящую из нескольких датчиков (измерительных каналов). В качестве примера возьмем неортогональную БИНС, описанную в еще одной моей статье (Неортогональная БИНС для малых БПЛА). Каждый из датчиков такой системы представляет собой отдельную динамическую систему, и в каждый конкретный момент времени он выдает одно скалярное измерение. Всего измерительных каналов восемь (по числу осей чувствительности акселерометров в блоке), а искомых параметров три (компоненты линейного ускорения измерительного блока).
Что нам известно о датчиках? У нас есть лишь записи сигналов с датчиков в статическом режиме. Т.е. для нас кто-то разместил блок акселерометров где-то в подвале и в течение, скажем, суток записывал значения проекции ускорения свободного падения на оси чувствительности акселерометров. Также пусть нам дали примерное значение матрицы направляющих косинусов датчиков в блоке.
Что от нас требуется? Составить алгоритм «Фильтра Калмановского Типа» (ФКТ), который давал бы оптимальные оценки линейного ускорения измерительного блока. Под оптимумом подразумевается минимум дисперсии ошибок оценивания и минимум их матожидания (минимум смещения «нуля» ошибок).
Примечание: используется название «Фильтр Калмановского Типа», потому что классический ФК подразумевает, что модель его совпадает с моделью реального объекта, а использование иной модели называется уже «Наблюдающим Устройством Идентификации Льюенбергера», относящимся к группе ФКТ.
Для подбора параметров моделей датчиков предлагается использовать генетические алгоритмы. Значения генов будут использоваться в качестве коэффициентов дифференциальных уравнений датчиков (см. «Объект идентификации» в ст. ТАУ-Дарвинизм):
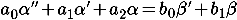
По этим коэффициентам будут строиться дискретные модели датчиков в пространстве-состояний (см. «Математическая модель» в ст. Фильтр Калмана — !cложно?):
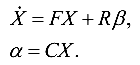
На основе этих моделей будет составляться «частный» фильтр Калмановского типа. Сборка из нескольких таких «частных» фильтров и образует федеративный ФКТ.
Функция приспособленности особи будет выдавать единицу, деленную на среднее значение квадратов ошибок оценивания:
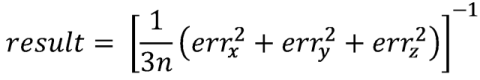
здесь n – количество шагов процесса моделирования фильтра (количество отсчетов в записанных сигналах).
Федеративный фильтр против Обобщенного
Концепцию составления обобщенного ФК (ОФК) я уже описывал (Фильтр Калмана — !cложно?). Подробно останавливаться не буду. Суть сводится к тому, что мы по дифференциальным уравнениям датчиков составляем модели в пространстве состояний. Далее мы должны составить блочно-диагональные матрицы ОФК, стыкуя матрицы моделей датчиков по диагонали. Т.е. такие матрицы
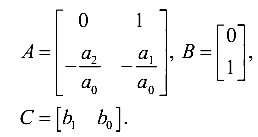
должны нам дать примерно следующее (для переходной матрицы)
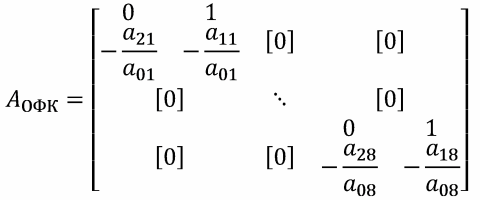
где вторым индексом коэффициентов обозначен номер датчика (измерительного канала).
Следующий важный момент – это вектор состояния ФК. Он, грубо говоря, содержит смещения маятников акселерометров (в рассматриваемой постановке задачи) и скорости их смещения. Нам же нужно вычислить какое ускорение нужно приложить к блоку, чтобы привести акселерометры в вычисленное с помощью ФК состояние. Для этого мы сначала должны вычислить сигналы смоделированных Фильтром Калмана акселерометров
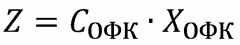
где
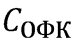 |
– блочно-диагональная матрица, составленная из матриц измерения моделей датчиков |
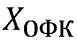 |
— вектор состояний всех датчиков в блоке |
После того, как мы получили вектор сигналов датчиков, нам остается как-то решить переопределенную систему восьми уравнений с тремя неизвестными
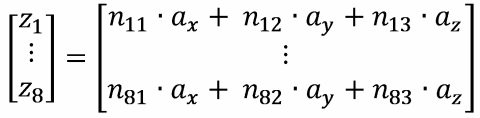
где
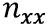 |
– направляющие косинусы осей чувствительности акселерометров |
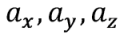 |
— искомые нами ускорения измерительного блока |
И тут внезапно…

Мы можем лишь вычислить псевдо-обратную матрицу, воспользовавшись гауссовско-марковским методом наименьших квадратов:
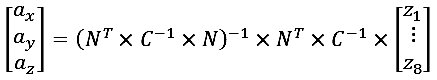
где N – это матрица направляющих косинусов (см. выше коэффициенты n11,n12, ..., n83);
C – матрица ковариаций ошибок измерений (не путать с Cофк).
Что плохого в алгоритме ОФК? В его переходной матрице много нулей, на которые не хочется тратить процессорное время. Как раз эту проблему и решает Федеративный алгоритм Фильтра Калмановского Типа. Суть проста. Мы отказываемся от составления одного фильтра, объединяющего сразу все датчики и реализуем восемь отдельных фильтров для каждого из датчиков. Т.е. вместо одного фильтра 16-го порядка используем 8 фильтров второго порядка. Схематично это можно изобразить следующим образом.
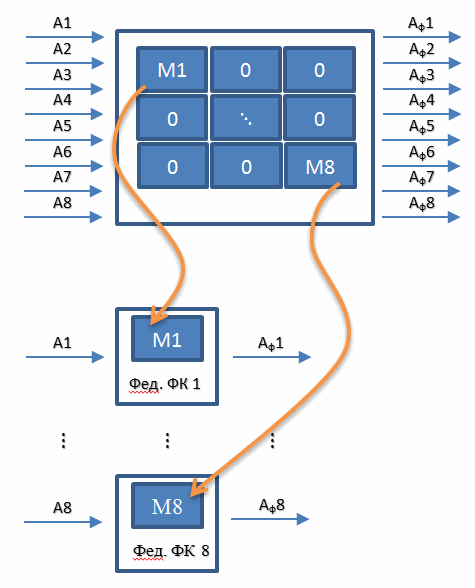
Выходные сигналы этих восьми «частных» фильтров мы также, как и в случае с ОФК подставляем в уравнение гауссовско-марковского МНК и получаем оценки трех компонентов ускорения измерительного блока.
В чем недостаток Федеративных фильтров Калмановского типа? В них в качестве матрицы ковариаций ошибок измерения используется матрица [1x1], содержащая дисперсию ошибки измерения одного единственного датчика. Т.е. вместо ковариационной матрицы используется скаляр, равный дисперсии шумов конкретного датчика. Таким образом, ковариации шумов между измерительными каналами не учитываются. Значит, такой фильтр должен быть менее эффективным в случае реальных, коррелированных между собой, шумов. Это в теории. На практике же ковариации шумов меняются во времени, потому дать гарантию того, что ОФК будет давать «более» оптимальную оценку, чем федеративный, нет возможности. Вполне может оказаться так, что эффективность ОФК будет ненамного выше или вообще равна эффективности федеративного фильтра. Это, кстати, мне еще предстоит исследовать.
Программа синтеза и симуляции
Структура солюшена
Заранее извиняюсь за англицизмы – не смог некоторым терминам из профессионального жаргона найти эквивалент в «великом и могучем». Итак, рассказ о программе начну с укрупненного описания структуры солюшена (извините). Потом опишу логику наиболее интересных на мой взгляд методов. В конце расскажу о том, как я генерировал исходные данные для программы.
Структура солюшена представлена на mind-map (флэшка с мозгами ?) ниже. Пунктирными стрелками показаны связи сборок (references).
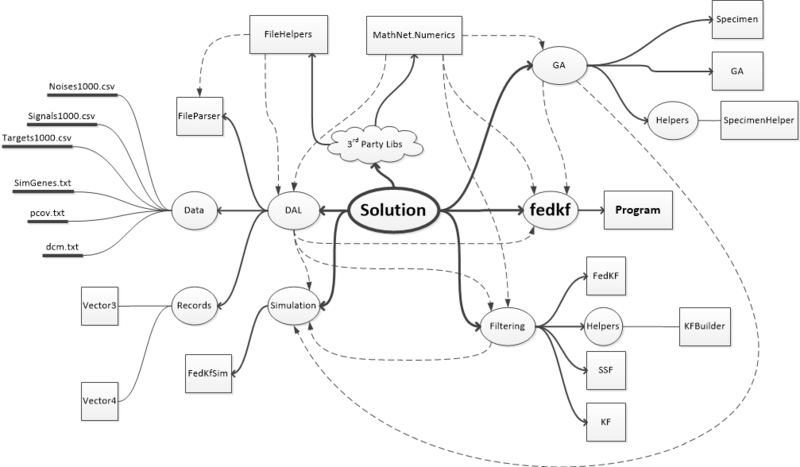
В программе использованы две сторонние библиотеки: Math.Net для матричной алгебры и генерации случайных чисел, а также FileHelpers для загрузки данных из CSV-фалов. Кроме того, реализованный движок генетических алгоритмов основан на сторонней реализации «A Simple C# Genetic Algorithm» (Barry Lapthorn). Правда, от оригинальной реализации осталось немного.
Солюшен содержит один проект консольного приложения и четыре проекта типа Class Library, содержащие основную логику.
Сборка GA, как можно догадаться по названию, содержит реализацию генетических алгоритмов. Она содержит структуру Specimen (структура данных особи) и классы GA и SpecimenHelper. SpecimenHelper является статическим классом и содержит статические методы, упрощающие работу с генами особи (например, GenerateGenes, Crossover, Mutate, Print). Также этот класс содержит экземпляры генераторов случайных чисел ContinuousUniform из библиотеки Math.Net. Этот генератор пришлось использовать, т.к. я выяснил, что стандартный генератор Random из сборок .Net 4.5 генерирует нормально распределенные случайные числа вместо равномерно распределенных. Для генерации генов это достаточно критично.
Класс GA инстанс-ориентирован. Можно создать несколько экземпляров оптимизатора с разными параметрами и функциями приспособленностями. К примеру, можно в одном движке делать подбор параметров математической модели датчиков, а во втором уже подбирать значения матриц ковариаций, при этом через замыкание «подсовывая» в функцию приспособленности самую лучшую на данный момент сборку параметров математической модели.
Сборка Simulation пока содержит только один статический класс FedKfSim. Тот, в свою очередь, содержит параметры симуляции федеративного фильтра, метод-расширение ToFedKf для экземпляра класса Specimen, создающий федеративный фильтр по генам данной особи. Так же этот класс содержит статический метод Simulate, в котором для переданной параметров особи создается федеративный фильтр и запускается процесс симуляции работы этого фильтра.
Сборка Filtering содержит реализации динамической модели в пространстве состояний (класс SSF), частного фильтра Калмановского типа (класс KF) и федеративного фильтра (класс FedKF). Класс SSF помимо инстанс-методов содержит два статических метода, позволяющих сгенерировать дискретную модель пространства состояний по коэффициентам непрерывной передаточной функции (ПФ). Параметры ПФ передаются в нотации MatLab, т.е.
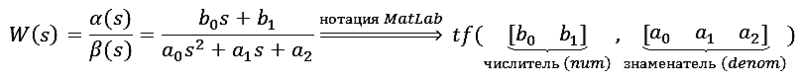
Статический класс KFBuilder в сборке Filtering содержит вспомогательные методы генерации модели пространства состояний и частного ФКТ, используя в качестве исходных данных строковые записи коэффициентов числителя и знаменателя непрерывной ПФ, а также требуемую частоту дискретизации (величину, обратную периоду квантования по времени).
В сборке DAL содержится класс FileParser, используемый для распарсивания текстовых файлов, содержащих матричные данные, а также для загрузки сигналов и шумов из CSV-файлов.
Движок генетических алгоритмов
Для его работы необходимо задать функцию приспособленности (FitnessFunction), размер популяции (PopulationSize), количество поколений (GenerationsCount), количество генов у особи (GenomeSize), вероятность скрещивания (CrossoverRate), вероятность мутации (MutationRate).
Метод Initiation предназначен для генерации начальной популяции особей. Код метода представлен ниже (оставлено лишь самое важное):
private void Initiation()
{
//...
_currGeneration = new List<Specimen>();
var newSpecies = Enumerable.Range(0, PopulationSize).AsParallel().Select(i =>
{
var newSpec = new Specimen
{
Length = this.GenomeSize
};
SpecimenHelper.GenerateGenes(ref newSpec);
var fitness = FitnessFunction(newSpec);
newSpec.Fitness = double.IsNaN(fitness) ? 0 : (double.IsInfinity(fitness) ? 1e5 : fitness);
//...
return newSpec;
}).OrderBy(s => s.Fitness);
_currGeneration = newSpecies.ToList(); // Huge load starts here :)
_fitnessTable = new List<double>();
foreach (var spec in _currGeneration)
{
if (!_fitnessTable.Any())
{
_fitnessTable.Add(spec.Fitness);
}
else
{
_fitnessTable.Add(_fitnessTable.Last() + spec.Fitness);
}
}
TotalFitness = _currGeneration.Sum(spec => spec.Fitness);
//...
}
Важный момент здесь – использование параллельного LINQ. Вначале создается массив индексов от 0 до размера популяции. Для этого перечислимого экземпляра создается параллельный запрос (.AsParallel()), к которому уже присоединяется select-запрос, в теле которого будет генерироваться экземпляр особи и вычисляться значение ее приспособленности. В конце присоединяется упорядочивающий запрос (.OrderBy(…)). Все это были запросы и выполнится этот блок кода быстро. Актуализация значений будет производиться в следующей строчке:
_currGeneration = newSpecies.ToList(); // Huge load starts here :)
о чем и говорит комментарий. При этом вычисления будут производиться параллельно с использованием пулла потоков, поэтому в теле select-запроса нельзя помещать код записи значений в какую-либо общую переменную (к примеру, в общий массив). Такой код сильно замедлит работу параллельного запроса (с этим мы еще столкнемся).
По сгенерированным особям вычисляется таблица приспособленности особей, которая нужна будет для алгоритма «Колесо Рулетки» выборки особей для скрещивания. Как видно из кода, каждое текущее (последнее) значение в таблице является суммой предыдущего значения и текущей приспособленности. Таким способом таблица заполняется отрезками разной длины – чем больше приспособленность тем больше длина отрезка (см. рисунок ниже).

Благодаря этому можно используя равномерно распределенную случайную величину в пределах от нуля до суммы всех приспособленностей «честно выбирать» особи для скрещивания так, чтобы наиболее приспособленные особи выбирались чаще, но и «лузеры» тоже имели шанс на скрещивание. Если же генератор случайных чисел будет выдавать нормально распределенные величины (как в случае с Random в .Net 4.5), то выбираться чаще всего будут особи из середины таблицы приспособленностей. Вот почему выше я и написал, что использование ContinuousUniform из пакета Math.Net было в моем случае критичным моментом.
Следующий метод, о котором хочется рассказать – это метод Selection.
private void Selection()
{
var tempGenerationContainer = new ConcurrentBag<Specimen>();
//...
for (int i = 0; i < this.PopulationSize / 2.5; i++)
{
int pidx1 = this.PopulationSize - i - 1;
int pidx2 = pidx1;
while (pidx1 == pidx2 || _currGeneration[pidx1].IsSimilar(_currGeneration[pidx2]))
{
pidx2 = RouletteSelection();
}
//...
var children = Rnd.NextDouble() < this.CrossoverRate ? parent1.Crossover(parent2) : new List<Specimen> { _currGeneration[pidx1], _currGeneration[pidx2] };
foreach (var ch in children.AsParallel())
{
if (double.IsNaN(ch.Fitness))
{
var fitness = FitnessFunction(ch);
var newChild = new Specimen
{
Genes = ch.Genes,
Length = ch.Length,
Fitness = double.IsNaN(fitness) ? 0 : (double.IsInfinity(fitness) ? 1e5 : fitness)
};
tempGenerationContainer.Add(newChild);
}
else
{
tempGenerationContainer.Add(ch);
}
}
}
_currGeneration = tempGenerationContainer.OrderByDescending(s => s.Fitness).Take(this.PopulationSize).Reverse().ToList();
//...
}
В этом методе производится селекция. Я не стал здесь выбирать обоих родителей с помощью колеса рулетки. Первый из родителей выбирается по порядку из чуть менее, чем половины наиболее приспособленных особей. Второй из родителей уже выбирается случайно. Причем если второй родитель по генам близок к первому, то случайная выборка повторяется, пока не будет получен достаточно отличающийся по генам родитель. Далее случайным образом запускается процедура скрещивания, которая выдает две особи со смешенными генами и еще одну, значения генов которой выбираются как среднее от значений генов родителей.
TODO: наверное, надо заменить вычисление среднего, вычислением случайного числа в диапазоне между значениями генов родителей.
После скрещивания у новых особей fitness будет иметь значение double.NaN. Актуализация значений приспособленности новых особей делается опять же параллельно
foreach (var ch in children.AsParallel())
{
if (double.IsNaN(ch.Fitness))
{
var fitness = FitnessFunction(ch);
var newChild = new Specimen
{
//...
};
tempGenerationContainer.Add(newChild);
}
//...
}
Последний метод движка ГА, о котором стоит рассказать, это метод RouletteSelection.
private int RouletteSelection()
{
double randomFitness = Rnd.NextDouble() * TotalFitness;
int idx = -1;
int first = 0;
int last = this.PopulationSize - 1;
int mid = (last - first) / 2;
while (idx == -1 && first <= last)
{
if (randomFitness < _fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > _fitnessTable[mid])
{
first = mid;
}
else if (randomFitness == _fitnessTable[mid])
{
return mid;
}
mid = (first + last) / 2;
// lies between i and i+1
if ((last - first) == 1)
{
idx = last;
}
}
return idx;
}
В этом методе с помощью метода половинного деления идет поиск отрезка в таблице приспособленностей, в который попадает случайно выбранное значение. Повторюсь, случайное число выбирается в диапазоне от нуля до суммы всех приспособленностей. Чем больше приспособленность конкретной особи, тем больше вероятность того, что случайно выбранное значение приспособленности попадет в соответствующий данной особи отрезок таблицы. Таким способом нужный индекс находится довольно быстро.
Симулятор Федеративного ФКТ
Как написано ранее, симулятор федеративного фильтра реализуется классом FedKfSim. Главным методом в нем является метод Simulate.
public static double Simulate(Specimen spec)
{
var fkf = spec.ToFedKf();
var meas = new double[4];
...
var err = 0.0;
int lng = Math.Min(Signals.RowCount, MaxSimLength);
var results = new Vector3[lng];
results[0] = new Vector3 { X = 0.0, Y = 0.0, Z = 0.0 };
for (int i = 0; i < lng; i++)
{
var sigRow = Signals.Row(i);
var noiseRow = Noises.Row(i);
var targRow = Targets.Row(i);
meas[0] = sigRow[0] + noiseRow[0];
meas[1] = sigRow[1] + noiseRow[1];
meas[2] = sigRow[2] + noiseRow[2];
meas[3] = sigRow[3] + noiseRow[3];
var res = fkf.Step(meas, inps.ToColumnWiseArray()); // inps в текущей реализации ФК не используются
var errs = new double[] { res[0, 0] - targRow[0], res[1, 0] - targRow[1], res[2, 0] - targRow[2] };
err += (errs[0] * errs[0]) + (errs[1] * errs[1]) + (errs[2] * errs[2])/3.0;
results[i] = new Vector3 { X = res[0, 0], Y = res[1, 0], Z = res[2, 0] };
...
}
...
return 1/err*lng;
}
В этом методе запускается итерационный процесс. На каждом шаге делается выборка чистых значений сигналов датчиков, шумов и референсных значений (ускорений блока без шумов). Чистые сигналы суммируются с шумами, и эта смесь подается на вход методу Step федеративного фильтра. Еще туда же подается оценка ускорений блока с прошлого шага, но в текущей реализации частного ФКТ эти значения не используются. Метод Step федеративного фильтра выдает массив значений – оценки ускорений блока. Разница между ними и значениями референса и будет текущей ошибкой оценивания. В конце текущего шага вычисляется средний квадрат ошибок оценивания, и полученное значение прибавляется к сумме ошибок. По окончании итераций вычисляется среднее значение ошибки по всем шагам процесса. На выход подается число, обратное к средней ошибке.
Исполняемое приложение
Последовательность работы приложения такова. Сначала делается проверка аргументов консоли. Если список аргументов не пустой, то производится попытка выполнения одной из допустимых команд.
switch (cmd)
{
case "simulate":
case "simulation":
InitializeSimulator();
FedKfSim.PrintSimResults = true;
var spec = new Specimen();
SpecimenHelper.SetGenes(ref spec, ReadSimulationGenes());
FedKfSim.Simulate(spec);
break;
case "set":
var settingName = args[1];
var settingValue = args[2];
var config = ConfigurationManager.OpenExeConfiguration(ConfigurationUserLevel.None);
config.AppSettings.Settings[settingName].Value = settingValue;
config.Save(ConfigurationSaveMode.Modified);
ConfigurationManager.RefreshSection("appSettings");
Console.WriteLine("'{0}' set to {1}", settingName, settingValue);
break;
case "print":
Console.WriteLine("Current settings:");
foreach (var name in ConfigurationManager.AppSettings.AllKeys.AsParallel())
{
var value = ConfigurationManager.AppSettings[name];
Console.WriteLine("'{0}' => {1}", name, value);
}
break;
case "help":
case "?":
case "-h":
PrintHelp();
break;
default:
Console.Error.WriteLine(string.Format("nARGUMENT ERRORn'{0}' is unknown command!n", cmd));
PrintHelp();
break;
}
По команде «simulate» производится вычитывание из файлов конфигурации значений генов, для которых нужно сгенерировать федеративный ФКТ. Команда «set» предназначена для изменения одного из значений в главном конфигурационном файле приложения. По команде «print» в консоль выводятся значения всех настроек из главного конфигурационного файла. Команда «help» выводит в консоль базовую документацию.
При запуске приложения без аргументов производится вычитывание из файла конфигурации основных параметров работы движка ГА, а также значения матриц, сигналов, шумов и референсов из файлов данных. После загрузки всех нужных данных и параметров создается экземпляр оптимизатора и запускается эволюционный процесс.
InitializeSimulator();
var genCount = int.Parse(ConfigurationManager.AppSettings["GenerationsCount"]);
var popSize = int.Parse(ConfigurationManager.AppSettings["PopulationSize"]);
var crossOver = double.Parse(ConfigurationManager.AppSettings["CrossoverRate"], FileParser.NumberFormat);
var mutRate = double.Parse(ConfigurationManager.AppSettings["MutationRate"], FileParser.NumberFormat);
var maxGeneVal = double.Parse(ConfigurationManager.AppSettings["MaxGeneValue"], FileParser.NumberFormat);
var minGeneVal = double.Parse(ConfigurationManager.AppSettings["MinGeneValue"], FileParser.NumberFormat);
var genomeLength = int.Parse(ConfigurationManager.AppSettings["GenomeLength"]);
SpecimenHelper.SimilarityThreshold = double.Parse(
ConfigurationManager.AppSettings["SimilarityThreshold"], FileParser.NumberFormat);
var ga = new Ga(genomeLength)
{
FitnessFunction = FedKfSim.Simulate,
Elitism = true,
GenerationsCount = genCount,
PopulationSize = popSize,
CrossoverRate = crossOver,
MutationRate = mutRate
};
FedKfSim.PrintSimResults = false;
ga.Go(maxGeneVal, minGeneVal);
Особое внимание здесь стоит уделить методу ReadSignalsAndNoises.
private static void ReadSignalsAndNoises()
{
var noisesPath = ConfigurationManager.AppSettings["NoisesFilePath"];
var signalsPath = ConfigurationManager.AppSettings["SignalsFilePath"];
var targetsPath = ConfigurationManager.AppSettings["TargetsFilePath"];
FedKfSim.Noises = new DenseMatrix(FileParser.Read4ColonFile(noisesPath));
FedKfSim.Signals = new DenseMatrix(FileParser.Read4ColonFile(signalsPath));
FedKfSim.Targets = new DenseMatrix(FileParser.Read3ColonFile(targetsPath));
var measCov = new DenseMatrix(4);
double c00 = 0, c01 = 0, c02 = 0, c03 = 0, c11 = 0, c12 = 0, c13 = 0, c22 = 0, c23 = 0, c33 = 0;
Vector<double> v1 = new DenseVector(1);
Vector<double> v2 = new DenseVector(1);
Vector<double> v3 = new DenseVector(1);
Vector<double> v4 = new DenseVector(1);
var s1 = new DescriptiveStatistics(new double[1]);
var s2 = new DescriptiveStatistics(new double[1]);
var s3 = new DescriptiveStatistics(new double[1]);
var s4 = new DescriptiveStatistics(new double[1]);
var t00 = Task.Run(() =>
{
v1 = FedKfSim.Noises.Column(0);
s1 = new DescriptiveStatistics(v1);
c00 = s1.Variance;
});
var t11 = Task.Run(() =>
{
v2 = FedKfSim.Noises.Column(1);
s2 = new DescriptiveStatistics(v2);
c11 = s2.Variance;
});
var t22 = Task.Run(() =>
{
v3 = FedKfSim.Noises.Column(2);
s3 = new DescriptiveStatistics(v3);
c22 = s3.Variance;
});
var t33 = Task.Run(() =>
{
v4 = FedKfSim.Noises.Column(3);
s4 = new DescriptiveStatistics(v4);
c33 = s4.Variance;
});
Task.WaitAll(new[] { t00, t11, t22, t33 });
var t01 = Task.Run(() => c01 = CalcVariance(v1, s1.Mean, v2, s2.Mean, FedKfSim.Noises.RowCount));
var t02 = Task.Run(() => c02 = CalcVariance(v1, s1.Mean, v3, s3.Mean, FedKfSim.Noises.RowCount));
var t03 = Task.Run(() => c03 = CalcVariance(v1, s1.Mean, v4, s4.Mean, FedKfSim.Noises.RowCount));
var t12 = Task.Run(() => c12 = CalcVariance(v2, s2.Mean, v3, s3.Mean, FedKfSim.Noises.RowCount));
var t13 = Task.Run(() => c13 = CalcVariance(v2, s2.Mean, v4, s4.Mean, FedKfSim.Noises.RowCount));
var t23 = Task.Run(() => c23 = CalcVariance(v3, s3.Mean, v4, s4.Mean, FedKfSim.Noises.RowCount));
Task.WaitAll(new[] { t01, t02, t03, t12, t13, t23 });
measCov[0, 0] = c00; measCov[0, 1] = c01; measCov[0, 2] = c02; measCov[0, 3] = c03;
measCov[1, 0] = c01; measCov[1, 1] = c11; measCov[1, 2] = c12; measCov[1, 3] = c13;
measCov[2, 0] = c02; measCov[2, 1] = c12; measCov[2, 2] = c22; measCov[2, 3] = c23;
measCov[3, 0] = c03; measCov[3, 1] = c13; measCov[3, 2] = c23; measCov[3, 3] = c33;
FedKfSim.SensorsOutputCovariances = measCov;
}
В нем для хранения значений ковариаций используется несколько отдельных переменных типа double. Как я написал выше, если бы я использовал один массив, то параллельные задачи (Task) выполнялись бы медленно. Собственно на этом я и накололся с изначальной реализацией данного метода. Я задавал внутри каждой задачи индексы, по которым следовало прописывать полученное значение ковариации в общем массиве. И с этой точки зрения код был, вроде бы, безопасен. Но выполнялся он крайне медленно. После замены массива отдельными переменными вычисление матрицы ковариаций значительно ускорилось.
Итак, что делается в этом методе? Для каждого уникального сочетания двух рядов шумов создается отдельная асинхронная задача. В этих задачах вычисляется взаимная вариация двух случайных процессов.
private static double CalcVariance(IEnumerable<double> v1, double mean1, IEnumerable<double> v2, double mean2, int length)
{
var zipped = v1.Take(length).Zip(v2.Take(length), (i1, i2) => new[] { i1, i2 });
var sum = zipped.AsParallel().Sum(z => (z[0] - mean1) * (z[1] - mean2));
return sum / (length - 1);
}
Формула аналогична формуле вычисления дисперсии. Только вместо квадрата отклонений от среднего одного случайного ряда используется произведение отклонений от средних значений двух отдельных рядов.
Исходные данные
Исходными данными для программы являются числовые ряды с шумами, сигналами датчиков и истинными значениями компонентов ускорения блока, а также параметры фильтра: матрица направляющих косинусов (взята из моего дипломного проекта, соответствует конфигурации избыточного блока, описанного в одной из моих прошлых статей), матрица ковариаций шумов процесса (задавалась эмпирическим путем).
Референсные значения ускорений блока были заданы в виде комбинации двух синусоид. Эти значения через матрицу направляющих косинусов блока были пересчитаны в сигналы датчиков. Шумы датчиков генерировались гибридным способом. Я взял запись сигнала реального датчика, находившегося во время записи в покое. Удалив из этого сигнала постоянную составляющую, я получил шумы датчика в статике (для отладки алгоритмов этого достаточно). Кстати говоря, шумы эти оказались очень близки к белым с нормальным распределением. Эти шумы я разрезал на короткие выборки из 1000 значений, отмасштабировал их интенсивности для приведения дисперсий к диапазону [0.05..0.15]. Таким образом, можно говорить, что я использовал реальные шумы в своих исследованиях.
Результаты
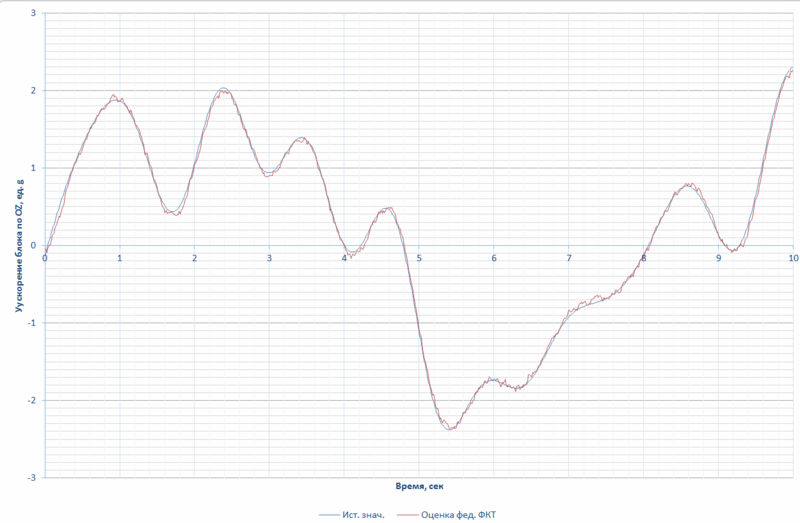
Сгенерированный федеративный фильтр уменьшил среднюю дисперсию шумов почти в два раза (т.е. уменьшил среднеквадратическую ошибку примерно в 1,38 раза). Можно было добиться еще более значительного уменьшения дисперсии ошибок увеличением инерционности, но тогда бы увеличилось динамическое запаздывание. На мой взгляд с помощью ГА был сгенерирован вполне работоспособный фильтр шумов.
Заключение
Свободного времени у меня не так много, поэтому при имплементации основного функционала было не до перфекционизма. Местами есть бреши в безопасности кода (в основном это касается валидации аргументов), местами не соблюдены общие рекомендации «C# Code Style Guide». Наверняка найдутся блоки кода с неоптимальной производительностью. Но несмотря на все ее недостатки, она работает достаточно хорошо. Я тестировал ее на ЦП Intel Core i3, и процесс оптимизации был довольно быстрым. К тому же благодаря использованию TPL ресурсы процессора использовались довольно эффективно. Реализованные алгоритмы потребляли практически все свободное время процессора, но благодаря нормальному приоритету асинхронных задач TPL остальные пользовательские программы работали без серьезных блокировок. Я запускал в консоли реализованную программу и переключался на работу в Visual Studio 2012 со встроенным решарпером, периодически переключался в Outlook и MS Word, отлаживал рабочий проект параллельно в браузерах IE и Chrome, серьезных тормозов при этом не наблюдая. В общем, это был хороший опыт использования библиотеки асинхронного программирования TPL, был сразу получен хороший результат без каких-либо серьезных трудностей.
Спасибо за внимание! Надеюсь статья и код будут Вам полезны.
Исходники на гитхаб: github.com/homoluden/fedkf-ga
Автор: HomoLuden






