В общем случае преобразование изображения в ASCII-графику представляет собой довольно трудоемкую задачу, однако существуют алгоритмы, позволяющие автоматизировать данный процесс. В данной статье рассматривается подход, предложенный исследователями Paul D. O’Grady и Scott T. Rickard в работе «Automatic ASCII Art Conversion of Binary Images Using Non-Negative Constraints». Описанный ими метод предполагает представление процесса преобразования изображения как задачи оптимизации и решение этой задачи при помощи неотрицательного матричного разложения. Ниже приведены описание рассматриваемого алгоритма, а также его реализация:
Описание алгоритма
Исходное изображение разбивается на блоки размером $inline$Mtimes N$inline$, где $inline$M$inline$ и $inline$N$inline$ — ширина и высота одного символа в пикселях. Если ширинавысота изображения не кратна шириневысоте символа, то картинка обрезается или дополняется белыми областями нужного размера.

Каждый из $inline$K$inline$ блоков, полученных после разбиения, представляется в виде вектора длиной $inline$R=M*N$inline$, значениями которого являются интенсивности цвета пикселей изображения (значения от 0 до 255, где белому пикселю соответствует значение 0, а черному — 255). Полученные векторы следует нормировать, используя норму $inline$l_2$inline$:
$$display$$v_i= frac{v_i}{sqrt{sum^R_{k=1}{v^2_k}}}$$display$$
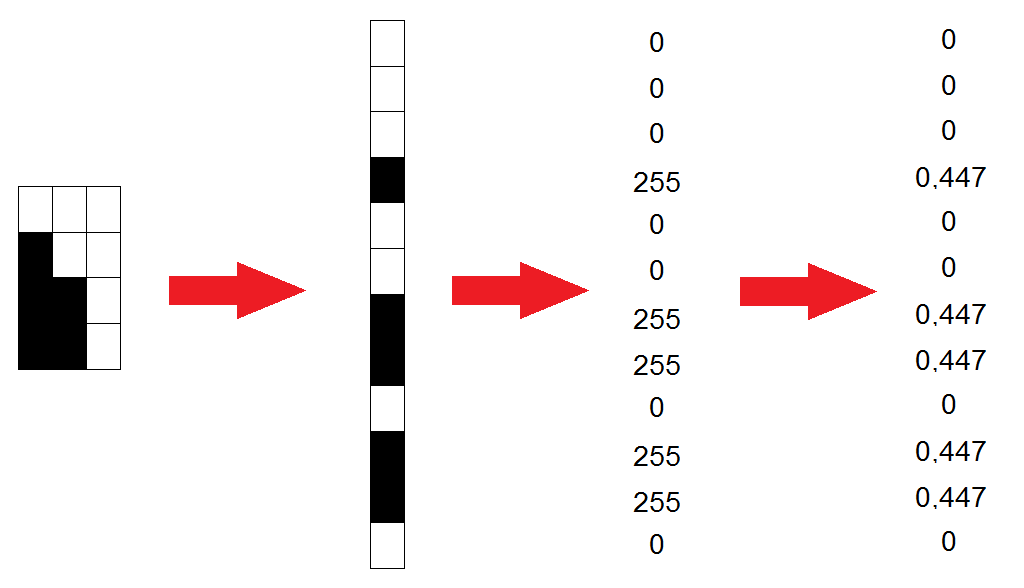
Нормированные векторы переписываются в виде столбцов, образуя таким образом матрицу $inline$V$inline$ размером $inline$Rtimes K$inline$.
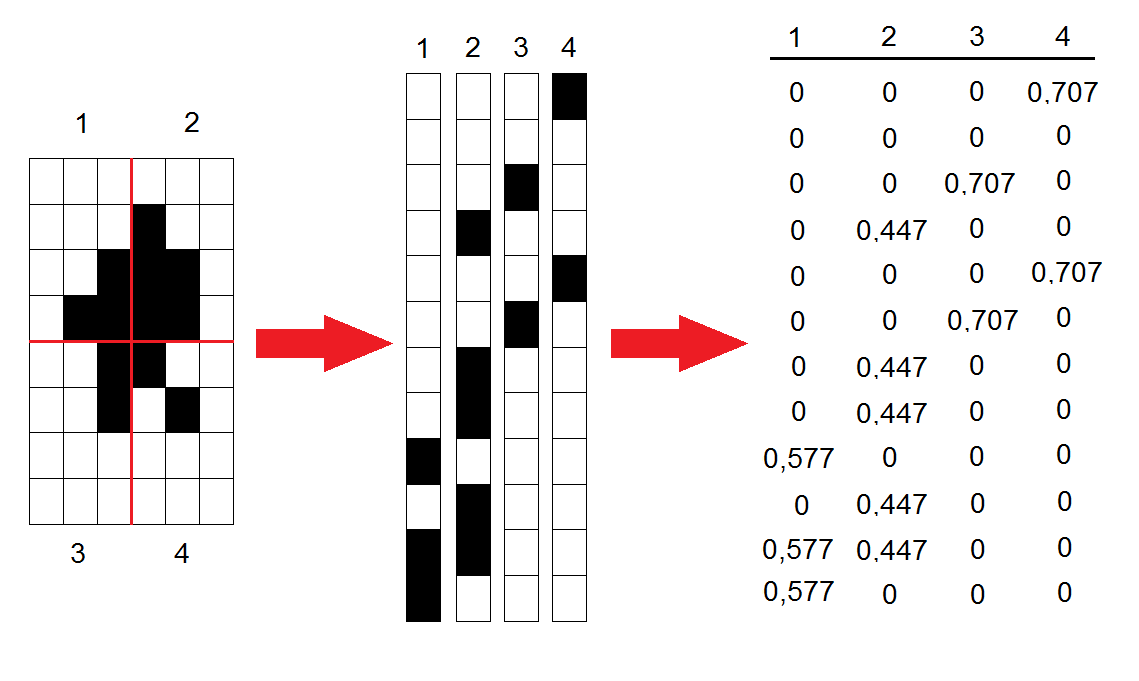
Полученную матрицу $inline$V$inline$ нужно представить в виде произведения матриц $inline$W$inline$ и $inline$H$inline$, все элементы которых неотрицательны:
$$display$$V_{R times K}=W_{Rtimes L} H_{L times K}$$display$$
Матрица $inline$W$inline$ известна заранее: она строится аналогично матрице $inline$V$inline$, но вместо участков исходной картинки используются изображения всех символов, используемых при генерации ASCII-графики. Если применяемый набор включает в себя $inline$L$inline$ символов, то матрица $inline$W$inline$ будет иметь размер $inline$Rtimes L$inline$.
Остается лишь подобрать матрицу $inline$H$inline$ таким образом, чтобы минимизировать значение некоторой целевой функции, характеризующей разницу между $inline$V$inline$ и произведением $inline$WH$inline$. В качестве такой функции используется следующая зависимость:
$$display$$D(V,W,H,beta)=sum_{ik}bigg({v_ikfrac{v_{ik}^{beta-1}-[WH]^{beta-1}_{ik}}{beta(beta-1)}}+[WH]^{beta-1}_{ik}frac{[WH]_{ik}-v_{ik}}{beta}bigg)$$display$$
Данное выражение по сути объединяет в себе несколько целевых функций: при $inline$beta = 2$inline$ оно преобразуется в квадрат евклидова расстояния (Squared Euclidean Distance), при $inline$beta rightarrow 1$inline$ приближается к расстоянию Кульбака-Лейблера (Kullback-Leibler Divergence), а при $inline$beta rightarrow 0$inline$ — к расстоянию Итакуры-Сайто (Itakura-Saito Divergence).
Непосредственно подбор матрицы $inline$H$inline$ производится следующим образом: $inline$H$inline$ инициализируется случайными значениями от 0 до 1, после чего ее значения итеративно обновляются согласно следующему правилу (количество итераций задается заранее):
$$display$$h_{jk}=h_{jk}frac{sum^R_{i=1}{w_{ij}frac{v_{ik}}{[WH]^{2-beta}_{ik}}}}{sum^R_{i=1}{w_{ij}[WH]^{beta-1}_{ik}}}$$display$$
Каждое значение $inline$h_{ij}$inline$ соответствует степени схожести $inline$i$inline$-го символа из используемого набора с $inline$j$inline$-м участком изображения.

Таким образом, чтобы определить, каким символом следует заменить $inline$j$inline$-й участок, достаточно найти максимальное значение в $inline$j$inline$-м столбце матрицы $inline$H$inline$. Номер строки, в котором располагается данное значение, и будет номером искомого символа в наборе. Кроме того, можно ввести некоторое пороговое значение $inline$epsilon$inline$, и если найденное максимальное значение меньше этого порога, то участок изображения заменяется пробелом. Использование пробела может положительно сказаться на виде результирующего изображения по сравнению с использованием символа с низкой степенью схожести.
Реализация
Реализация алгоритма выполнена на языке C#. Для генерации ASCII-графики используются 95 символов (от 0x20 до 0x7E) размером 11x23 пикселей; применяемый шрифт — Courier. Ниже представлен исходный код функции преобразования исходного изображения в ASCII-графику:
public static char[,] ConvertImage(
Bitmap image,
double beta,
double threshold,
ushort iterationsCount,
ushort threadsNumber,
Action<int> ProgressUpdated)
{
int charNumHor = (int)Math.Round((double)image.Width / glyphWidth);
int charNumVert = (int)Math.Round((double)image.Height / glyphHeight);
int totalCharactersNumber = charNumVert * charNumHor;
int glyphSetSize = wNorm.ColumnCount;
Matrix<double> v = SplitImage(image, charNumVert, charNumHor);
Matrix<double> h = Matrix<double>.Build.Random(
glyphSetSize,
totalCharactersNumber,
new ContinuousUniform());
int progress = 0;
ushort step = (ushort)(iterationsCount / 10);
for (ushort i = 0; i < iterationsCount; i++)
{
UpdateH(v, wNorm, h, beta, threadsNumber);
if((i + 1) % step == 0)
{
progress += 10;
if(progress < 100)
{
ProgressUpdated(progress);
}
}
}
var result = GetAsciiRepresentation(h, charNumVert, charNumHor, threshold);
ProgressUpdated(100);
return result;
}
Рассмотрим каждый ее шаг по отдельности:
1) Вычислим, какое количество символов можно уместить по ширине и по высоте изображения:
int charNumHor = (int)Math.Round((double)image.Width / glyphWidth);
int charNumVert = (int)Math.Round((double)image.Height / glyphHeight);
Используя рассчитанные значения, разобьем исходное изображение на блоки необходимого размера. Для каждого блока запишем значения интенсивности цвета пикселей в соответствующий столбец матрицы $inline$V$inline$ (при необходимости расширим исходное изображение, добавив в матрицу нулевые значения, соответствующие белым пикселям), после чего нормализуем все столбцы:
private static Matrix<double> SplitImage(
Bitmap image,
int charNumVert,
int charNumHor)
{
Matrix<double> result = Matrix<double>.Build.Dense(
glyphHeight * glyphWidth,
charNumHor * charNumVert);
for (int y = 0; y < charNumVert; y++)
{
for (int x = 0; x < charNumHor; x++)
{
for (int j = 0; j < glyphHeight; j++)
{
for (int i = 0; i < glyphWidth; i++)
{
byte color = 0;
if ((x * glyphWidth + i < image.Width) &&
(y * glyphHeight + j < image.Height))
{
color = (byte)(255 - image.GetPixel(
x * glyphWidth + i,
y * glyphHeight + j).R);
}
result[glyphWidth * j + i, charNumHor * y + x] = color;
}
}
}
}
result = result.NormalizeColumns(2.0);
return result;
}
2) Заполним матрицу $inline$H$inline$ случайными значениями от 0 до 1:
Matrix<double> h = Matrix<double>.Build.Random(
glyphSetSize,
totalCharactersNumber,
new ContinuousUniform());
Применим к ее элементам правило обновления заданное количество раз:
for (ushort i = 0; i < iterationsCount; i++)
{
UpdateH(v, wNorm, h, beta, threadsNumber);
if((i + 1) % step == 0)
{
progress += 10;
if(progress < 100)
{
ProgressUpdated(progress);
}
}
}
Непосредственно обновление элементов матрицы реализовано следующим образом (к сожалению, проблемы, связанные с делением на ноль, решаются при помощи некоторых костылей):
private static void UpdateH(
Matrix<double> v,
Matrix<double> w,
Matrix<double> h,
double beta,
ushort threadsNumber)
{
const double epsilon = 1e-6;
Matrix<double> vApprox = w.Multiply(h);
Parallel.For(
0,
h.RowCount,
new ParallelOptions() { MaxDegreeOfParallelism = threadsNumber },
j =>
{
for (int k = 0; k < h.ColumnCount; k++)
{
double numerator = 0.0;
double denominator = 0.0;
for (int i = 0; i < w.RowCount; i++)
{
if (Math.Abs(vApprox[i, k]) > epsilon)
{
numerator +=
w[i, j] * v[i, k] / Math.Pow(vApprox[i, k], 2.0 - beta);
denominator +=
w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0);
}
else
{
numerator += w[i, j] * v[i, k];
if (beta - 1.0 > 0.0)
{
denominator +=
w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0);
}
else
{
denominator += w[i, j];
}
}
}
if (Math.Abs(denominator) > epsilon)
{
h[j, k] = h[j, k] * numerator / denominator;
}
else
{
h[j, k] = h[j, k] * numerator;
}
}
});
}
3) Последний шаг состоит в выборе для каждого участка изображения подходящего символа путем нахождения максимальных значений в столбцах матрицы $inline$H$inline$:
private static char[,] GetAsciiRepresentation(
Matrix<double> h,
int charNumVert,
int charNumHor,
double threshold)
{
char[,] result = new char[charNumVert, charNumHor];
for (int j = 0; j < h.ColumnCount; j++)
{
double max = 0.0;
int maxIndex = 0;
for (int i = 0; i < h.RowCount; i++)
{
if (max < h[i, j])
{
max = h[i, j];
maxIndex = i;
}
}
result[j / charNumHor, j % charNumHor] =
(max >= threshold) ? (char)(firstGlyphCode + maxIndex) : ' ';
}
return result;
}
Полученное изображение записывается в html-файл. Полный исходный код программы можно найти тут.
Примеры сгенерированных изображений
Ниже представлены примеры изображений, сгенерированных при различных значениях параметра $inline$beta$inline$ и количествах итераций. Исходное изображение имело размер 407x500 пикселей, соответственно результирующие изображения имели размер 37x22 символов.
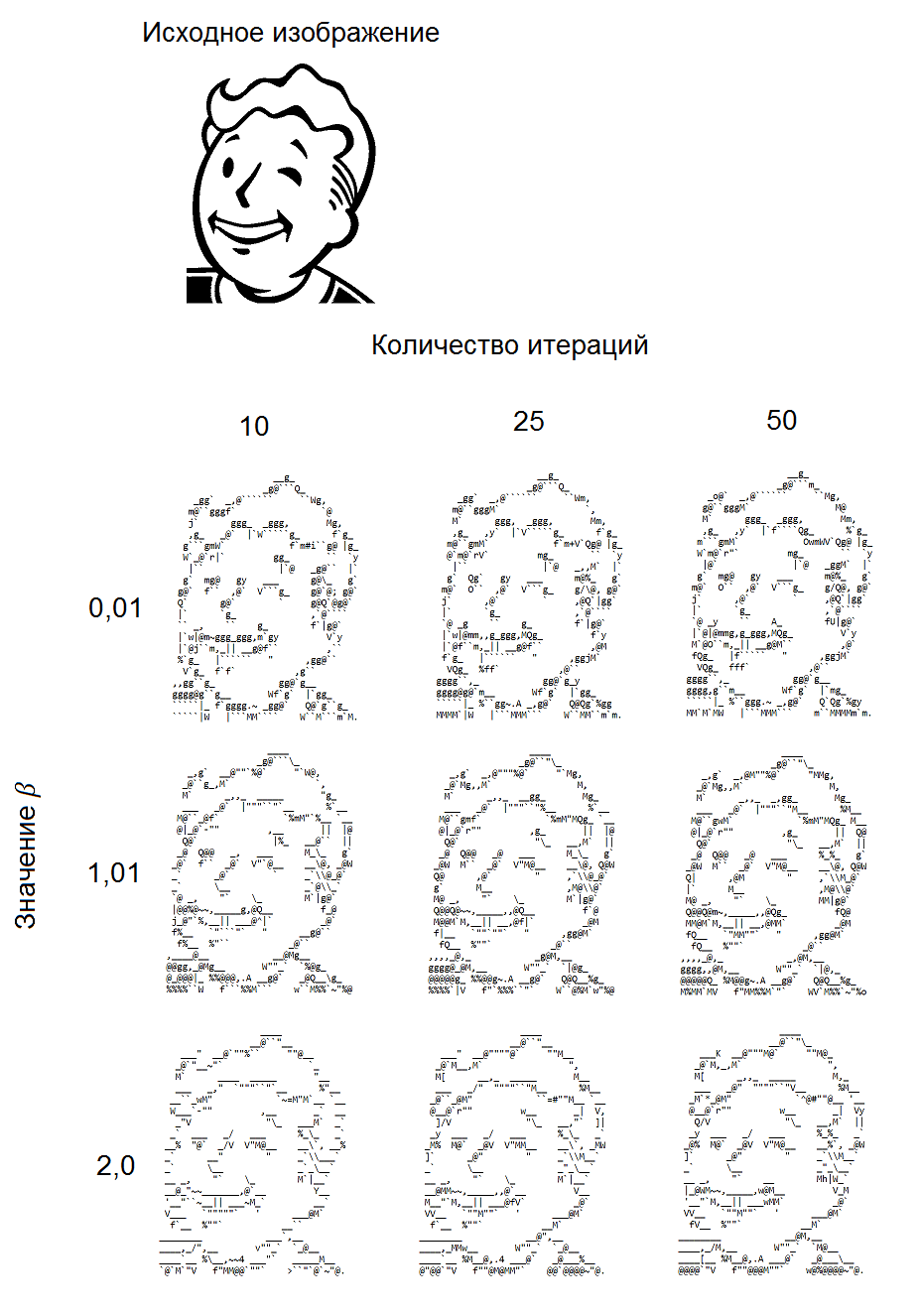
Заключение
В рассматриваемом алгоритме можно выделить следующие недостатки:
- Долгая обработка изображений: в зависимости от размера картинки и количества итераций ее обработка может занимать от нескольких десятков секунд до нескольких десятков минут.
- Низкое качество обработки детализированных изображений. Например, попытка преобразования изображения человеческого лица дает следующий результат:

В то же время уменьшение количества деталей за счет увеличения яркости и контрастности изображения позволяет значительно улучшить вид результирующего изображения:

В целом несмотря на перечисленные недостатки можно сделать вывод о том, что алгоритм дает удовлетворительные результаты.
Автор: Muttnik