Несколько дней назад случилась конференция Hydra. Ребята из JUG.ru Group пригласили спикеров мечты (Лесли Лэмпорт! Клифф Клик! Мартин Клеппманн!) и посвятили два дня распределённым системам и вычислениям. Контур был одним из трёх партнёров конференции. Мы общались на стенде, рассказывали про наши распределённые хранилки, играли в бинго, решали задачки.
Это пост с разбором задач на стенде Контура от автора их текста. Кто был на Гидре — это ваш повод вспомнить приятные впечатления, кто не был — шанс размять big O-нотацией.
Были даже участники, которые разобрали флипчарт на слайды, чтобы записать своё решение. Я не шучу — они сдали на проверку вот такую пачку бумаги:

Всего было три задачи:
- о выборе реплик по весам для балансировки нагрузки
- о сортировке результатов запроса к in-memory базе данных
- о передаче состояния в распределённой системе с кольцевой топологией
Задача 1. ClusterClient
Нужно было предложить алгоритм эффективного выбора K из N взвешенных реплик распределённой системы:
Your team is tasked with developing a client library for a massively distributed cluster of N nodes. The library would keep track of various metadata associated with nodes (e.g., their latencies, 4xx/5xx response rates, etc.) and assign floating point weights W1..WN to them. In order to support the concurrent execution strategy, the library should be able to pick K of N nodes randomly—a chance of being selected should be proportional to a node’s weight.
Propose an algorithm to select nodes efficiently. Estimate its computational complexity using big O notation.
Потому что в таком виде с ними боролись участники конференции и потому что английский был официальным языком Гидры. Выглядели задачки так:
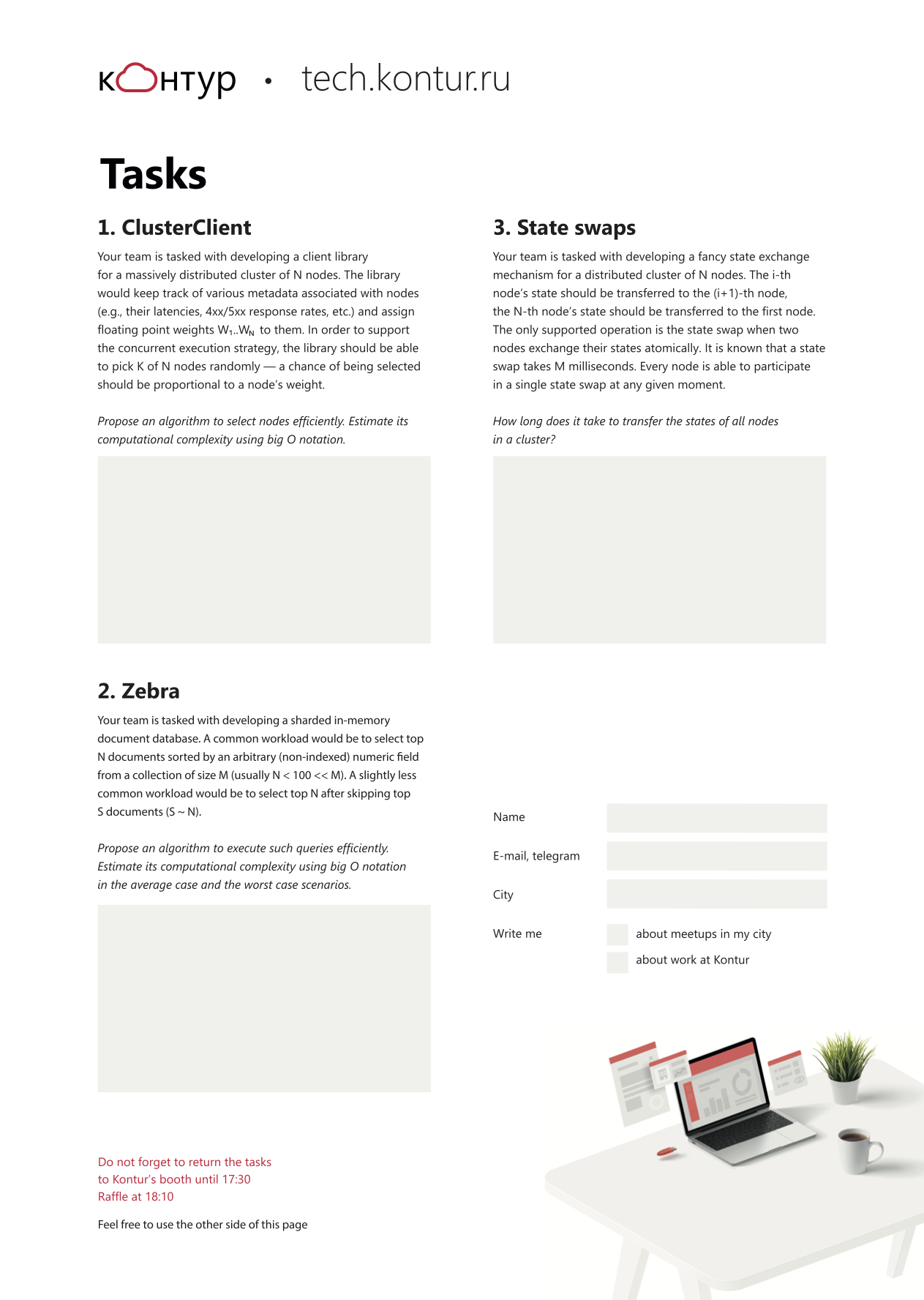
Возьмите бумагу и карандаш, подумайте, не торопитесь сразу открывать спойлеры :)
Начало в 5:53, всего 4 минуты:
А вот как питчили своё решение те самые ребята с флипчартом:
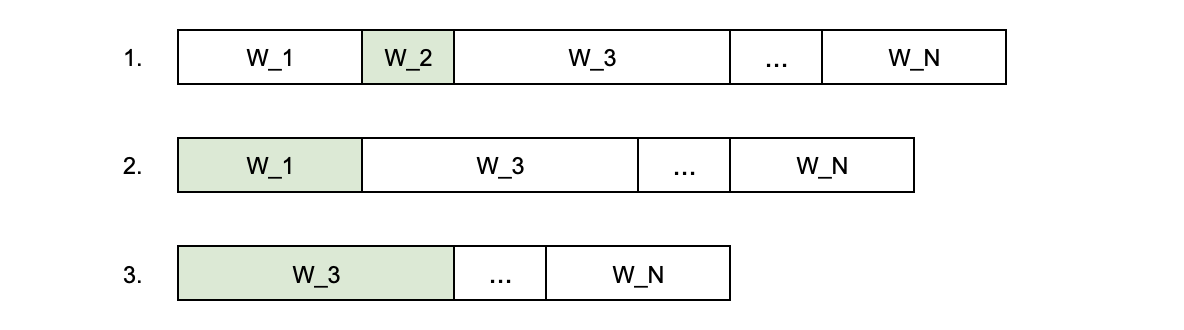
На поверхности лежит такое решение: просуммировать веса всех реплик, сгенерировать случайное число от 0 до суммы всех весов, затем выбрать такую i-реплику, что сумма весов реплик от 0 до (i-1)-ой меньше случайного числа, а сумма весов реплик от 0 до i-ой — больше него. Так получится выбрать одну реплику, а чтобы выбрать следующую, нужно повторить всю процедуру, не рассматривая выбранную реплику. С таким алгоритмом сложность выбора одной реплики — O(N), сложность выбора K реплик — O(N·K) ~ O(N2).
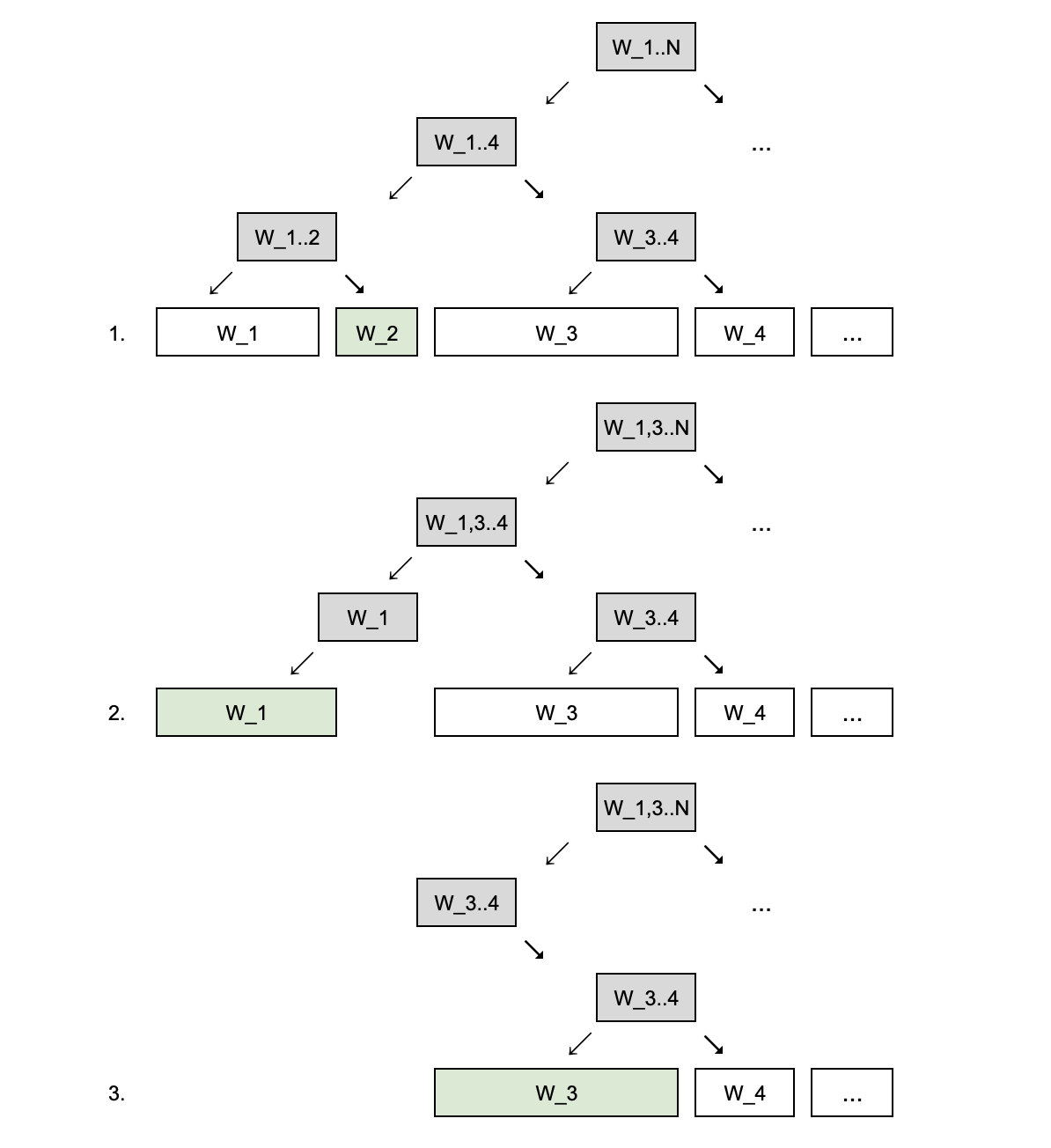
Квадратичная сложность — это плохо, однако её можно улучшить. Для этого построим дерево отрезков для сумм весов. Получится дерево глубиной lg N, в листьях которого будут веса реплик, а в остальных узлах — частичные суммы, вплоть до суммы всех весов в корне дерева. Далее генерируем случайное число от 0 до суммы всех весов, находим i-ую реплику, удаляем её из дерева и повторяем процедуру для поиска оставшихся реплик. С таким алгоритмом сложность построения дерева — О(N), сложность поиска i-ой реплики и удаления её из дерева — O(lg N), сложность выбора K реплик — O(N + K lg N) ~ O(N lg N).
Линейно-логарифмическая сложность приятнее квадратичной, особенно для больших K.
Именно этот алгоритм реализован в коде библиотеки ClusterClient из проекта «Восток». (Там дерево строится за O(N lg N), но на итоговую сложность алгоритма это не влияет.)
Задача 2. Zebra
Нужно было предложить алгоритм эффективной сортировки документов в памяти по произвольному неиндексированному полю:
Your team is tasked with developing a sharded in-memory document database. A common workload would be to select top N documents sorted by an arbitrary (non-indexed) numeric field from a collection of size M (usually N < 100 << M). A slightly less common workload would be to select top N after skipping top S documents (S ~ N).
Propose an algorithm to execute such queries efficiently. Estimate its computational complexity using big O notation in the average case and the worst case scenarios.
Начало в 34:50, всего 6 минут:
Решение на поверхности: отсортировать все документы (например, с помощью quicksort), затем взять N+S документов. В таком случае сложность сортировки в среднем — O(M lg M), в худшем — O(M2).
Очевидно, что сортировать все M документов, чтобы затем взять только небольшую часть от них — неэффективно. Чтобы не сортировать все документы, подойдёт алгоритм quickselect, который выберет N+S нужных документов (их можно будет отсортировать любым алгоритмом). В этом случае сложность в среднем уменьшится до O(M), а худший случай останется тем же.
Однако, можно сделать ещё эффективнее — воспользоваться алгоритмом binary heap streaming. В этом случае первые N+S документов складываются в min- или max-heap (в зависимости от направления сортировки), а затем каждый следующий документ сравнивается с корнем дерева, где содержится минимальный или максимальный на текущий момент документ, и при необходимости добавляется в дерево. В этом случае сложность в худшем случае, когда придётся постоянно перестраивать дерево — O(N lg N), сложность в среднем — O(N), как и при использовании quickselect.
Однако heap streaming оказывается эффективнее за счёт того, что на практике большую часть документов получается отбросить, не перестраивая кучу, после единственного сравнения с её корневым элементом. Такая сортировка реализована в документной in-memory базе данных Zebra, разработанной и используемой в Контуре.
Задача 3. State swaps
Нужно было предложить самый эффективный алгоритм для сдвига состояний:
Your team is tasked with developing a fancy state exchange mechanism for a distributed cluster of N nodes. The i-th node’s state should be transferred to the (i+1)-th node, the N-th node’s state should be transferred to the first node. The only supported operation is the state swap when two nodes exchange their states atomically. It is known that a state swap takes M milliseconds. Every node is able to participate in a single state swap at any given moment.
How long does it take to transfer the states of all nodes in a cluster?
Решение на поверхности: обменять состояния первого и второго элемента, затем первого и третьего, затем первого и четвёртого и так далее. После каждого обмена состояние одного элемента будет оказываться на нужной позиции. Придётся сделать O(N) перестановок и потратить O(N·M) времени.
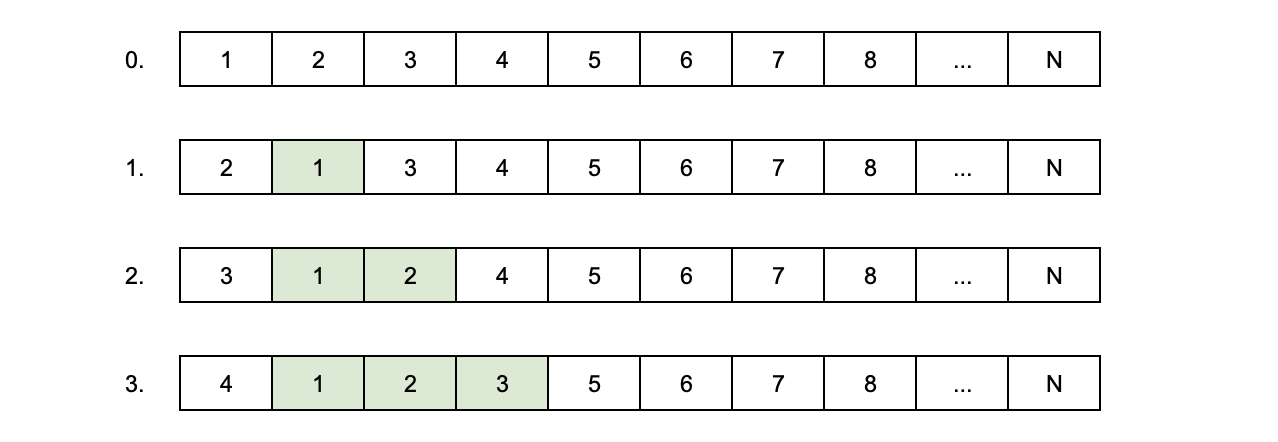
Линейное время — это долго, поэтому можно обменивать состояния элементов попарно: первого со вторым, третьего с четвёртым и так далее. После каждого обмена состояния каждого второго элемента будет оказываться на нужной позиции. Придётся сделать O(lg N) перестановок и потратить O(M lg N) времени.
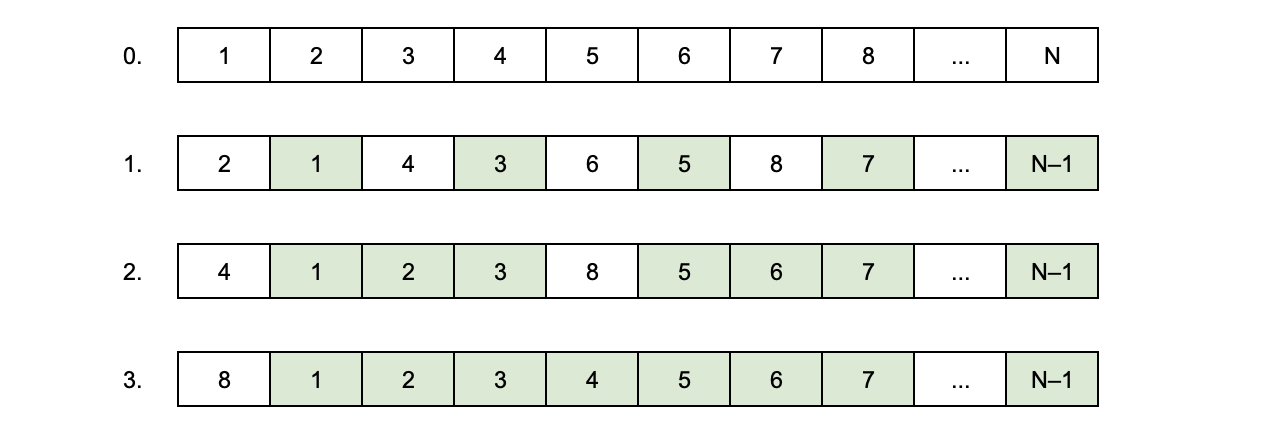
Однако, можно сделать сдвиг ещё эффективнее — не за линейное, а за константное время. Для этого на первом шаге нужно обменять состояние первого элемента с последним, второго с предпоследним и так далее. Состояние последнего элемента окажется на нужной позиции. А теперь нужно обменять состояние второго элемента с последним, третьего с предпоследним и так далее. После этого раунда обменов состояния всех элементов окажутся на нужной позиции. Всего будет сделано O(2M) ~ O(1) перестановок.
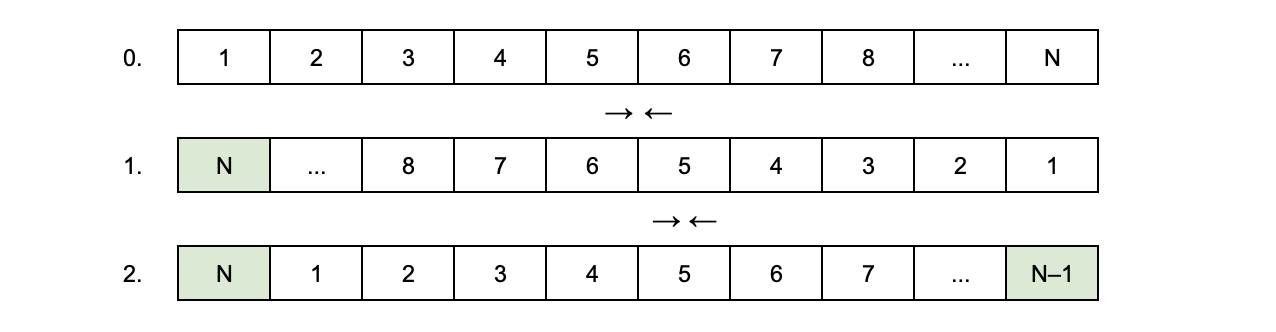
Такое решение совершенно не удивит математика, который ещё помнит, что поворот — это композиция двух осевых симметрий. Кстати, оно тривиально обобщается для сдвига не на одну, а на K < N позиций. (Напишите в комментариях, как именно.)
Понравились задачки? Знаете другие решения? Делитесь в комментариях.
А вот несколько полезных ссылок напоследок:
- узнайте больше об инфраструктурной разработке в Контуре
- посмотрите записи внутренних летучек с докладами о распределённых системах
- посмотрите цикл видеолекций «Необычные алгоритмы для обычных людей»
- подпишитесь на наш канал в Телеграме
Автор: Игорь Луканин