Привет. В этом посте мы продолжим экспериментировать с ограниченной машиной Больцмана. В предыдущем посте о регуляризации в РБМ мы увидели как можно получить более локальные фичи, которые обладают большей обобщающей способностью. Но мы не оценили их робастность по сравнению с более простыми и быстрыми алгоритмами. Для этого эксперимента мы обратимся к линейному методу главных компонент (вы можете ознакомиться с этим методом и глянуть реализацию на c# в моем первом посте). Желающим ознакомиться с первоисточником по теории сжатия размерности с использованием РБМ рекомендую глянуть статьи Джеффри Хинтона тут и тут. Мы же продолжим тестирование на множестве печатных больших букв: обучим РБМ, построим главные компоненты, сгенерируем сжатые представления данных, а из них восстановим первоначальные изображения, и затем оценим разницу между оригинальными изображениями и восстановленными.
Линейные главные компоненты
Подразумевается что вы знакомы с методом главных компонент, если нет, то вам сюда. Для этого эксперимента я использую множество изображений 29 на 29 пикселей, на которых изображены большие буквы английского алфавита четырех разных шрифтов и трех стилей, а так же эти же изображения с шумами, итого 4056 изображений. Тестовое множество состоит из того же набора букв, но с большим количеством шумов — 3432 штук. Итак приступим, на языке R код выглядит совсем просто: m.pca <- eigen(cov(m)). Важность главных компонент можно оценить по их главным значениям, сперва их нормализировав суммой этих значений. В итоге получатся следующие графики. На первом показано какой процент вариативности описывает каждый главный компонент, на втором изображена сумма объясненной вариации на каждом шаге.
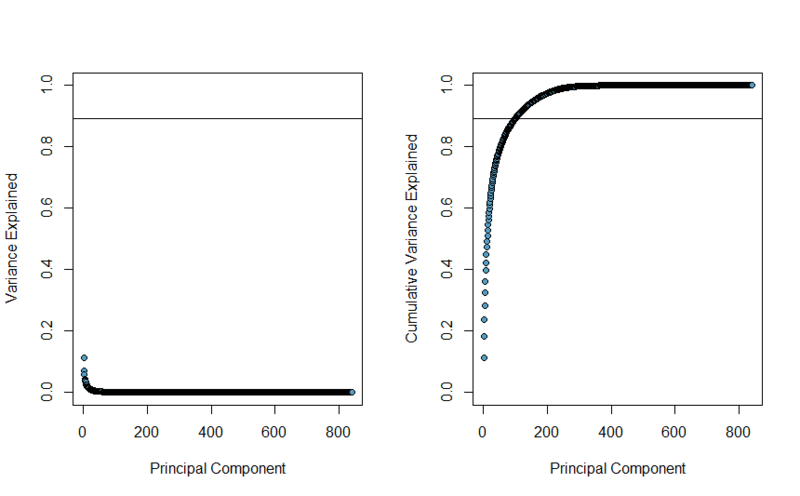
В РБМ мы будем использовать 100 скрытых состояний, так что для честности мы выберем первые 100 главных компонент, которые объясняют 89.36% вариативности, этот уровень изображен линией на графиках приведенных выше.
Каждый главный компонент можно интерпретировать как изображение 29 на 29 пикселей, которое детектирует некоторые особенности множества данных. Можно провести аналогию с весами скрытых нейронов ограниченной машины Больцмана, и визуализировать так же как мы это делали в предыдущих постах. Напомню, что на втором изображении черный цвет соответствует нулевому значению, увеличение красной составляющей — увеличение значения в положительную сторону, синей, соответственно — в отрицательную.
Порядок главных компонент слева направо, сверху вниз. Фичи получились довольно таки крупные, каждая из них имеет примерно средний размер буквы из обучающего множества. На счет интерпретации речи вообще не идет, ну за исключением нескольких первых компонент.
Restricted Boltzmann machine
Для этого эксперимента я использовал настройки описанные в предыдущем посте для L1 регуляризации, единственное что было изменено это обучающее множество (на описанное выше) и количество итераций стало 5000, это заняло около 14 часов (чую пора переписывать на GPU). К этому моменту ошибка кроссвалидации все еще падала, так что обучение можно было продолжать. В итоге получились следующие веса.
Как видите фичи очень локальные, в основном это примитивы типа небольших пятен и пограничных линий, объединив некоторые из них можно изучить топологические особенности образов из обучающего множества. Из-за их локальности можно строить очень малые рецепторные поля нейронов, т.е. обнулить до 95% весов каждого нейрона, что в разы увеличит скорость работы алгоритма проецирования данных, что действительно важно.
Восстанавливающая способность
Давайте взглянем на некоторые примеры изображений восстановленных с помощью двух моделей. В первом столбце оригинальные изображения, во втором восстановленные с помощью PCA, в третьем с помощью RBM.
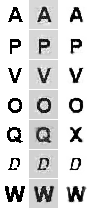
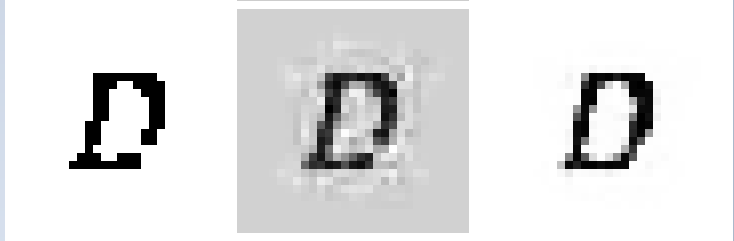
Когда я увидел, что фон в PCA-реконструкциях слишком серый, я попробовал по аналогии с eigenface, делать нормализацию средним значением, но в итоге восстановленные изображения не сильно отличались от приведенных выше. На увеличенном примере видно, что вдоль границ изображение размыто, хотя в случае PCA немного больше.
В качестве оценки расстояния между изображениями мы будем использовать L1-метрику:
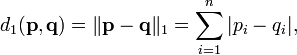
Результат получился следующий, напоминаю что тестовое множество не участвовало ни в построении модели РБМ, ни в вычислении главных компонент:
| PCA | RBM | |
|---|---|---|
| Train set | 29.134736802449488 | 21.79797897303671 |
| Test set | 49.231927648058118 | 29.970740205433025 |
Как видите результат в обоих случаях на стороне RBM.
Заключение
В РБМ несколько путей для улучшения качества. Во-первых я остановил обучение на 5000 итерации, хотя можно было бы продолжать обучение скажем до тех пор пока ошибка кроссвалидации не начнет расти. Во-вторых можно продолжать играться с параметрами обучения. В-третьих фичи довольно таки локальные, что может повысить скорость работы алгоритма. В-четвертых, легко заметить, что многие фичи в РБМ почти идентичны, что дает нам возможность кластеризовать фичи и объединить кластеры, что бы не вычислять их значение несколько раз, либо обучить РБМ с меньшим количеством скрытых нейронов.
Автор: mephistopheies
