Введение
«Что получится, если мы заменим числа с плавающей запятой на рациональные числа и попытаемся отрендерить изображение?»
Такой вопрос я задал себе после размышлений над твитом исследователя и преподавателя компьютерной графики Моргана Макгвайра. Он рассуждал о том, насколько сильно студенты компьютерных наук удивляются, когда впервые узнают, что для хранения привычных нам чисел с плавающей запятой в современных компьютерах нужно идти на компромиссы. И эти компромиссы делают сложными простые задачи, например, проверку принадлежности точки треугольнику. Проблема, разумеется, заключается в том, что проверка нахождения четырёх точек в одной плоскости (копланарности) с помощью определителя или какого-нибудь векторного умножения (а на самом деле это одно и то же) никогда не даст значение, точно равное нулю, чего требуют эти математические методы. Даже если бы настоящие вычисления нахождения на одной плоскости были бы точны, те же компромиссы с точностью почти с вероятностью в 1,0 дали бы ответ, что сами четыре точки не копланарны.
Это зародило во мне мысль — если допустить, что все входящие данные рендерера (координаты вершин, 3D-преобразования и т.д.) были бы заданы как рациональные числа, то создавали бы все операции, от создания луча, обхода ускоряющей структуры и до пересечения лучей с треугольниками только рациональные числа? Если это было бы так, то мы бы смогли выполнять проверку копланарности совершенно точно! Возможно, вы зададитесь вопросом, почему 3D-сцена, выраженная в рациональных числах должна давать результаты тоже только в рациональных числах…

Простая сцена, трассировка пути в которой выполнена рациональной арифметикой. Здесь используется система чисел «с плавающей чертой дроби», а не числа с плавающей запятой.
Во-первых, рациональное число — это такое число, которое можно выразить как соотношение двух целых чисел, например 1/2 или 355/113. Во-вторых, «обычные операции рендеринга», такие как проверки ограничивающих параллелограммов (bounding box tests), проверки пересечения луча с треугольником, отражения луча и т.д., основаны на векторных и скалярных произведениях, а также скалярном делении (это включает в себя преобразования координат и обращение матриц, кватернионы и т.д.), которые в свою очередь основаны на четырёх основных операциях: сложении, вычитании, умножении и делении. При сложении, вычитании, умножении и делении рациональных чисел тоже получаются рациональные числа. Математик бы сказал, что множество рациональных чисел образует поле, замкнутое под четырьмя основными арифметическими действиями. Для нас это означает, что если придерживаться исключительно рациональных чисел, то можно и в самом деле перейти от входящих данных 3D-сцены к полностью отрендеренному изображению, не покидая при этом мира рациональных чисел.
Исключениями из правила «действия над рациональными числами дают рациональные числа» являются квадратные корни и тригонометрические/трансцедентальные функции. Что касается последних, то я всегда говорю, что если вам пришлось выполнять в геометрических внутренностях своего рендерера тригонометрические вычисления, то скорее всего вы что-то делаете не так (и я показывал, как исправить наиболее стандартные случаи). Что касается квадратных корней, то за исключением конических сечений (сфер, цилиндров и т.д.) и выполнения затенения/ДФОС/раскраски не требуется нормализовать лучи и нормали к поверхностям так часто, как это обычно делается. Уж точно не нужно этого делать для создания луча, его прохождения, пересечения, отражений и т.д. К сожалению, очень часто я вижу, что программисты нормализуют величины без каких-либо причин, кроме «ну не знаю, я делаю так, чтобы подстраховаться». На практике, в той части рендеринга, где выполняется трассировка геометрии, очень редко нужно нормализовать значения, поэтому у меня была надежда, что можно оттрассировать всю сцену, не покидая мир рациональных чисел — это то, что я бы назвал «рациональным рендерингом».
Чтобы применить это на практике, мне нужно создать систему чисел, основанную на рациональных числах, которую мог бы использовать компьютер. Тогда поверх неё я смог бы реализовать обычные алгоритмы трассировки пути, вычислять изображения без потери точности, выполнять проверки копланарности, имеющие точные ответы, и осчастливить всех студентов, изучающих компьютерную графику.
Эта статья — история о двух вечерах исследований реалистичности такой идеи. Я расскажу о множестве аспектов, которые узнал, о том, что я придумал и о нескольких сюрпризах, которые обнаружил в процессе. Статья написана в более-менее хронологическом порядке моей работы. Кроме того, она написана в моём необычно неформальном и очень ненаучном стиле (чем я горжусь). Показанное выше изображение — своего рода спойлер, но дочитайте статью до конца, потому что я расскажу и о хорошем, и о плохом.
Подготовка
Первое, что я сделал — реализовал в Shadertoy ограниченный до минимума трассировщик для сверхпростой сцены, состоящей из плоскости, сферы, параллелограмма и треугольника — строительных блоков реальных рендереров. Затем я скопипастил код в файл C++ и, внеся пару незначительных изменений, скомпилировал его с помощью своего фреймворка piLibs. Так я получил для сравнения трассированное изображение, отрендеренное на ЦП с использованием обычных чисел по стандарту IEEE754 с плавающей запятой. Также я убрал из кода трассировки все нормализации лучей, потому что, как и говорилось выше, ни одна из них на самом деле не нужна. Напомню, что для нормализации требуется квадратный корень, а рациональные числа при его использовании не сохраняются (квадратный корень рационального числа рациональным числом не является). Чуть позже мы увидим, что применять квадратные корни, разумеется, всё равно можно, просто я хотел сделать код как можно более математически чистым, чтобы посмотреть, как далеко я могу зайти с точной арифметикой рациональных чисел без округлений.
Последний подготовительный шаг — я взял все vec3, mat4x4 и прочие базовые классы алгебры/математики, а затем изменил их таким образом, чтобы они использовали «rational» вместо «float». Так как моя структура «rational» перегружает все стандартные операторы (add, sub, mul, div, смену знака, сравнения и т.д.), замена произошла без проблем. Я быстро реализовал оставшиеся обычные операции (abs, sign, mod, fract, floor, sqrt, и т.д.), которых теоретически было достаточно для получения красивых рациональных рендеров.
Тест 1 — наивное решение
Но давайте посмотрим, какой была эта первая реализация. Сначала я всегда пробую самое простое, а потом смотрю на результаты. И простейшим способом реализации рациональных значений было использование двух целых чисел. Как можно понять из названия раздела, это не будет моим окончательным решением, но для первой попытки это было разумное решение. Итак, каждое число x должно было быть представлено как числитель N и знаменатель D, образующие значение N/D. Значение x аппроксимируется наилучшей возможной парой N/D (в пределах заданной битовой глубины), которая наиболее близка к истинному значению x. Я решил, что оба числа обязательно должны быть положительными, а знак числа нужно хранить в отдельном бите, чтобы упростить работу и избавиться от неоднозначностей, хоть это и не очень важно. На этом этапе и числители, и знаменатели имели беззнаковый тип. Но даже при отделении знака N/D имели много избыточности: например, 1/4 и 7/28 обозначают одно и то же число, но имеют совершенно разные битовые представления. Мы коснёмся этого позже, а пока давайте не будем заострять внимание и посмотрим, как выглядят четыре основных арифметических действия в этом рациональном виде.
Во-первых, заметим, что вычитание a — b является просто сложением a и значения, противоположного b, т.е., a + (-b), где -b можно вычислить простой заменой знака b. Аналогично этому, деление a/b — это то же самое, что перемножение a и значения, обратного b. Или, другими словами, a/b = a · (1/b), где (1/b) можно вычислить простой переменой мест числителя bn и знаменателя bd числа b. Итак, вот первое интересное свойство рациональной арифметики — деление и умножение имеют одинаковые затраты, поэтому в отличие от обычного рендеринга с плавающей запятой, в котором деления обычно избегают, откладывают или скрывают под задержками медленных запросов получения текстур, в рациональной арифметике этих операций бояться не нужно.
Перейдём к сложению с умножением: мы знаем, что противоположные и обратные значения вычислить тривиально просто, поэтому получаем:
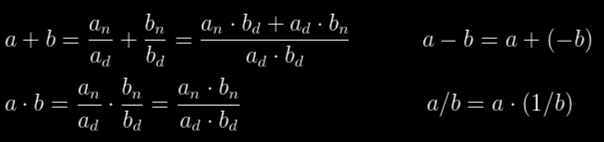
Сохранение знака при умножении выполняется тривиально, это всего лишь xor, потому что два положительных значения дают положительный результат, как и два отрицательных. Сохранение знака для сложения — более сложный процесс и для быстрого решения я реализовал его через три ветвления (сложение тривиально, если знаки a и b совпадают, но когда они не совпадают, то нужно выбрать меньшее число и вычесть его из большего — в статье я не буду больше подробно описывать такие небольшие детали, а просто выложу куда-нибудь исходный код).
Также я пропущу реализацию fract() и floor(); если вы решите попробовать реализовать их самостоятельно, то увидите их простоту и красоту. Внимание также стоит уделить операторам сравнения. Позаботившись о знаках и приняв, что a и b положительны, мы получим
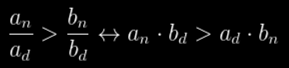
Здесь важно заметить, что даже для сравнения нам требуется пара операций умножения, что может привести к переходу к следующему размеру слова и окажется важным чуть ниже.
Наконец, мы рассмотрим квадратные корни в отдельном разделе, зная о том, что по большей части они нам не нужны (за исключением сферы из этого первого теста).
Этого было достаточно для запуска первого рендера и трассировки тестовой сцены (плоскость+сфера+треугольник+параллелограмм), чтобы посмотреть, что из этого получится. Я щедро использовал для этого первого теста 65-битные рациональные числа, что на самом деле представляет большой объём данных (сравнимый с типом данных «double»): 32 бита занимает числитель, 32 бита — знаменатель, и ещё один бит — знак. Первым идёт изображение, полученное при таком наивном подходе, вторым — изображение, сделанное с использованием чисел с плавающей запятой (эталонное):

«Наивные» 65-битные рациональные числа

Эталон с плавающей запятой
Результат оказался довольно плохим, параллелограмм и треугольник даже не появились на рендере, а сфера и плоскость пола были слишком шумными. Проблема, разумеется, заключалась в том, что каждый раз, когда мои рациональные числа выполняли любую основную арифметическую операцию на любом из алгоритмических этапов рендеринга, числитель и знаменатель бесконтрольно становились всё больше и больше, потому что использовалось целочисленное умножение. Подумайте о следующем: если бы единицами измерения нашего исходного мира были метры, и мы бы привязывали исходную геометрию (вершины и камеру) к миллиметровой точности, то только исходные данные заняли для довольно маленькой сцены 16-битный объём. В то же самое время при стандартном разрешении экрана HD и сглаживании 4X рациональные числа направления луча запросто бы потребовали 12 бит. То есть при первом взаимодействии луча и геометрии самая простая арифметическая операция, использующая оба набора входящих данных, превратила бы результат в числа 28-битной длины — достаточно близко к 32-битному ограничению, которое я задал себе в этой первой реализации. И это ещё до того, как мы выполнили самое первое векторное или скалярное произведение. К моменту завершения скалярного произведения рендереру для представления чисел уже потребовались бы рациональные числа длиной сотни бит. Разумеется, это наихудший случай, но и средний случай был бы близок к этому. Учитывая то, что под числитель и знаменатель я выделил всего 32-битную ёмкость, легко понять, как быстро в этом тесте значения выходят за границы — неудивительно, что за исключением плоскости пола и части сферы почти ничего не видно.
Тест 2 — сокращение на наибольший общий делитель
Затем я улучшил систему, задействовав то свойство, которое вкратце упоминал выше — разные рациональные числа могут обозначать одинаковую величину. И в самом деле, 6/12 — это то же значение, что и 1/2, однако оно использует гораздо больше битов, чем последнее. Поэтому идея заключалась в следующем: если после каждой основной арифметической операции (или после неё) я бы извлекал все общие делители из числителя и знаменатели, и приводил дробь к её простейшему виду, то, возможно, мне удастся держать всё под контролем и дольше продолжать операции с точной арифметикой без потери точности. Возможно, получится делать это достаточно долго, чтобы получить чистые отрендеренные изображения? Я сделаю небольшое отступление, чтобы показать ещё один пример: 588/910 можно упростить до 42/65, потому что 14 является делителем и 588, и 910. Но для хранения 42/65 очевидно нужно меньше битов, чем 588/910. Нахождение наибольшего возможного числа, одновременно делящего два других числа, можно выполнить с помощью алгоритма наибольшего общего делителя (Great Common Divisor, GCD), эффективные реализации которого вы можете найти где угодно (лично я скопировал её прямиком из Википедии и немного ускорил, выполняя этап сканирования битов с помощью внутренних операций x64). Итак, вооружённый алгоритмом НОД, мой класс «rational» должен постоянно упрощать дроби, генерируемые в процессе рендеринга. Это можно было делать двумя способами:
Первый — преобразовывать промежуточный результат операторов сложения и умноения в следующий тип битовых данных (в моём текущем наивном решении это uin64_t), выполнять поиск НОД в этом более объёмном типе данных, а затем снижать результат до исходной битовой длины (32). Второй способ — анализировать, как an, ad, bn и bd сочетаются друг с другом в обоих арифметических операторах и извлекать из них общие делители до выполнения умножения. Второй подход в принципе устранял необходимость использования больших битовых длин. Зная, что возможно их всё равно придётся использовать, я решил выбрать первый способ, потому что его проще реализовать и он позволял мне ускорить свою работу (вечер пролетает очень быстро). Сделав всё это, давайте посмотрим, какой рендер мне удастся создать теперь:

65-битные рациональные числа с сокращением на НОД

Эталон с плавающей запятой
Намного лучше! Пока далеко от идеала, конечно, но выглядит многообещающе. Я заставил появиться параллелограмм и треугольник, а сфера кажется теперь намного объёмнее. Однако в правом верхнем углу появился забавный артефакт, а рациональные числа для многих пикселей всё равно выходят за границы, что приводит ко множеству точек на изображении. Однако стоит заметить, что для некоторых (многих) пикселей я начал получать точные и идеальные результаты! То есть трассировщик нашёл математически точные пересечения точек и расстояний, что и являлось первопричиной того, чтобы попробовать использовать рациональные числа.
Прежде чем переходить к следующему шагу в процессе доказательства применимости рациональных чисел, я хочу ненадолго остановиться и поделиться своими находками относительно НОД и сокращения рациональных чисел.
Первое открытие связано с битовым объёмом рациональных чисел. Даже хотя я всё ещё не могу рендерить красивые изображения и этого добиться важнее, чем волноваться об оптимизации объёмов данных, и хотя в этой ранней реализации по-прежнему использовалось большое количество битов (1+32+32), я уже раздумывал над упоминавшейся ранее тратой битов в виде избыточных дробей. В частности, после добавления этапа с НОД, сочетания битов наподобие 2/4 уже не являются применимыми, потому что они автоматически сокращаются до 1/2 ещё до записи в любой регистр или переменную. То есть в каком-то смысле из всех 264 сочетаний битов, которые могли быть числителем и знаменателем, многие остались незадействованными. А тратить так биты впустую нельзя. Или можно? Сколько же места я на самом деле теряю? Я сделал небольшое отступление, чтобы исследовать этот вопрос.
Отступление — о взаимно простых числах
На иллюстрациях ниже показано использование битов для рациональных чисел в 5/5 битах и 7/7 битах. Горизонтальная и вертикальная оси графиков представляют значения числителя и знаменателя всех возможных рациональных чисел, имеющих числители и знаменатели вплоть до 5 бит (31) и 7 бит (127). Чёрные пиксели — это неиспользуемые сочетания, а белые пиксели — применяемые дроби. Например, вся диагональ чёрная, за исключением пикселя 1/1, потому что все дроби вида n/n сокращаются до 1/1.

Использование битов для 5/5 rational

Использование битов для 7/7 rational
Если посчитать пиксели, как это сделал я, то можно быстро понять, что доля полезных пикселей при увеличении количества бит стремится к 60,8%. Небольшое онлайн-исследование показало мне, что это соотношение оказывается точно равным 6/π2, потому что это также вероятность быть взаимно простыми (не иметь общих делителей) для двух случайных чисел. Вы можете спросить, откуда здесь взялось «пи»? Оказывается, что «шесть на „пи“ в квадрате» — это значение, равное единице, делённой на дзета-функцию Римана, вычисленную в точке 2, 1/ζ(2). Это не очень должно нас удивлять, потому что дзета-функция Римана часто всплывает в задачах с участием простых и взаимно простых чисел.
Как бы то ни было, похоже, что в своём рациональном представлении я впустую трачу примерно 40% сочетаний битов. И хотя это кажется большим числом, я решил смотреть на него так, как будто это на самом деле меньше бита… благодаря чему мог не особо расстраиваться. Учтя это, я решил двигаться дальше, используя другие, совершенно отличные подходы, вместо того, чтобы пытаться локально оптимизировать эту единственную проблему. Однако всё-таки я вкратце узнал о деревьях Штерна-Броко и Калкина-Уилфа, которые могли бы мне позволить полностью использовать все доступные биты, но получаемый с их помощью интервал значений оказывается очень маленьким, поэтому я быстро отказался от этой идеи и двинулся дальше. Думаю, на этом моменте я должен выразить признательность Википедии как постоянному источнику моих знаний.
Вернёмся к анализу того, что мы получили: я могу рендерить изображения с искажениями, но очень сильно завишу от распределения простых чисел в вычислениях. От этих простых чисел зависит, сможет ли алгоритм НОД упростить выражение — как только любое простое число или кратное ему попадает в любое из чисел рендерера (векторы, скаляры, матрицы), оно «загрязняет» все числа, следующие за ним в дальнейших арифметических манипуляциях, и остаётся в них навечно. Поэтому постепенно всё гарантированно начнёт разрастаться, это только вопрос времени. Кроме того, что это неизбежно, это ещё и необходимо, потому что именно взаимно простые делители несут в себе информацию о значении числа. Но в то же самое время большие простые числа очень быстро всё ломают. Так что тут есть конфликт.
Последнее, что стоит заметить — я по-прежнему использовал в два раза больше битов, чем стандартное число с плавающей запятой, так что пока реальных преимуществ здесь нет. Разумеется, я пытался использовать 16/16-битные рациональные числа, что было бы более честным сравнением с истинными требованиями к арифметике с плавающей запятой, но при точности 16/16 написанная мной система с числителем+знаменателем+НОД создавала совершенно неразборчивые изображения.
Тест 3 — нормализация рациональных чисел
Итак, на этом моменте мне необходимо было нечто действительно значительное. Казалось, что для предотвращения выхода чисел за границы нужно начинать урезать числа и терять точность. Весь мой эксперимент начался с идеи исследования точного рендеринга, но к этому моменту я чувствовал, что готов отказаться от этой идеи и продолжить исследовать другие области, хотя бы ради развлечения, и посмотреть, к чему это меня приведёт (исходная идея, стимулирующая к процессу исследования — это именно идея для начала процесса, и после неё вы часто в результате оказываетесь в совершенно неожиданном месте. Или, как сказал однажды Джон Клиз, плохие идеи могут привести к хорошим идеям, процесс творчества необязательно всегда является последовательностью или прогрессией логически верных шагов).
Как бы то ни было, я решил проверить, что бы случилось с рендерами, если бы я каким-то образом защитил числитель и знаменатель от переполнения. Проще всего было бы сдвигать и числитель, и знаменатель при необходимости на достаточное количество битов вправо, пока они снова не окажутся в выделенном им битовом пространстве. По сути, это означает целочисленное деление и числителя, и знаменателя на одну величину, а значит, значение числа остаётся приблизительно неизменным. И здесь я отклонился от исходной цели эксперимента.
В своей первой реализации я смотрел на количество битов, необходимых для числителя и знаменателя, брал максимум для обоих, и сдвигал оба на это количество битов (выполняя при этом округление до ближайшего целого числа). Когда это было реализовано в операторах сложения и умножения, всё начало выглядеть вполне приемлемо:

65-битные рациональные числа с сокращением на НОД и нормализацией

Эталон с плавающей запятой
Так как всё выглядело довольно неплохо, на этом этапе я приступил к решению проблемы большого объёма используемых в текущей реализации битов. Я попробовал использовать вместо 32/32 (65 бит) 16/16 (33 бита), и изображения оказались на удивление хорошими! Я всё ещё видел, что в некоторых рёбрах сферы есть небольшие отверстия, а на рисунке текстуры треугольника есть небольшие разрывы. Но это неплохо для величин, достаточно близких к числам с плавающей запятой. Это придало мне энергии для изучения новых идей.
Тест 4 — плавающая черта дроби
На этом этапе я решил отвлечься и перестать искать оправдания — если я хочу найти что-то интересное для рендеринга в рациональных числах, то они должны занимать 32 бита и не больше. Лучше найти хорошую идею или остановиться, и на этом закончить (это было в начале второго вечера экспериментов).
Сначала я подумал, что стоит придерживаться идей НОД и нормализации, но при этом умнее подходить к хранению и использованию битов. Первое, что пришло мне в голову — даже хотя числитель и знаменатель могут становиться большими, часто этого не происходит. Или, по крайней мере, это происходит не одновременно. Поэтому когда числитель мал, можно позволить знаменателю быть большим, и наоборот. Неиспользуемые биты одного из двух целых значений можно использовать для представления бОльших значений. Затем я осознал, что аналогично этому число с плавающей запятой по сути является форматом с фиксированной запятой, где «фиксированная» запятая сделана переменной. Я могу взять свои рациональные числа и тоже сделать битовое расположение черты дроби переменной. То есть не жёстко задавать дробь как 16/16, а позволить той же 32-битной переменной иногда быть 16/16, а иногда 5/27 или 13/19, по необходимости.
Это стоило проверить. Всё равно несколько строк кода упаковки/распаковки во внутренних сеттерах и геттерах можно написать быстро. Наиболее логичной схемой для меня показалась 1|5|26, то есть:
1 бит: знак
5 битов: позиция черты дроби (B)
26 бита: объединённые данные числителя и знаменателя; числитель — это верхние 26-B бит, знаменатель — нижние B бит,
где черта дроби (B) определяет размер знаменателя. Например, число 7/3 будет записываться как
7/3 = 0 00010 000000000000000000000111 11,
где знак 0 означает положительное значение, черта дроби 2 обозначает знаменатель (число 3), для представления которого нужно 2 бита, а остальная часть битов отходит к числителю.
Те читатели, которые работали со стандартом IEEE754, могут найти это наблюдение знакомым: двоичное представление знаменателя всегда начинается с «1», потому что число черты дроби всегда усекает его до кратчайшего представления. То есть первый бит знаменателя хранить необязательно. В этом случае число «3» можно представить только двоичным значением «1» и значением черты дроби «1»:
7/3 = 0 00001 0000000000000000000000111 1
Этот трюк не только сэкономил мне один драгоценный бит, но и имеет один превосходный побочный эффект: когда значение черты дроби равно нулю, это естественным образом одновременно означает, что знаменатель равен 1 и что для его хранения не нужно места. Это значит, что мое рациональное представление чисел внезапно оказалось полностью совместимым с обычным целочисленным представлением и арифметикой, пока значения чисел не поднимаются выше 226, то есть до достаточно большого порога. Какой прекрасный сюрприз! То есть теоретически я могу использовать точно такой же тип данных, «rational», для выполнения стандартных операций рендеринга и затенения, но также и выполнять всю логику и задачи потока команд в трассировщике пути — мне не нужно больше использовать два типа данных, как это бывает в большинстве рендереров («int» и «float») и выполнять преобразования в одну и другую стороны! Однако время меня поджимало, поэтому я не стал менять все индексы циклов с «int» на «rational». Вечер подходил к концу, а мне ещё предстояло проверить множество вещей для улучшения качества рендеров.
Создав реализацию, я смог проверить её:

32-битные рациональные числа с плавающей чертой дроби (1|5|26)

32-битный эталон с плавающей запятой
О-о-о, неплохо! У меня по-прежнему имеются артефакты в сфере, которые я пока буду считать виной своей плохой реализации квадратного корня, но параллелограмм и треугольник стали по-настоящему чистыми. Количество точно решённых пикселей изображения тоже повысилось. Думаю, благодаря тому, что до переполнения в знаменателе или числителе успевают появиться числа побольше, я увеличил вероятность того, что НОД найдёт общие делители и выполнит сокращение. То есть плавающая черта дроби не только увеличила интервал представляемых чисел и отложила момент нормализаций (с потерями точности), вызванных переполнением, но и сделала следующий шаг в улучшении качества благодаря повышению вероятности сокращений.
На этом этапе я был готов провести более серьёзную проверку (но пока всё ещё экспериментальную — до готовой к эксплуатации системы ещё далеко). Я реализовал трассировщик пути с минимальным набором функций (необязательно физически точный или даже учитывающий физику) и создал сцену с несколькими параллелограммами и двумя источниками освещения, эталонная реализация которой на GPU находится здесь: https://www.shadertoy.com/view/Xd2fzR.
Я снова сконвертировал сцену во фреймворк C++, опять удалил несколько ненужных нормализаций лучей и запустил рендер. Вот что я получил:

32-битные рациональные числа с плавающей чертой дроби

32-битный эталон с плавающей запятой
Ого, вот это действительно неплохо! Хоть и явно заметны протечки света в углах, где соединяются рёбра пола и потолка. Посмотрите на них в приближении:



Возможно, они вызваны проблемой в моей реализации пересечения луча и параллелограмма, которая только выражена в рациональных числах; я бы этому не удивился. А может быть, я упёрся в границы того, на что способны рациональные числа. Как бы то ни было, я вполне доволен. К тому же, у меня есть другие изменения и эксперименты, которые я хотел проверить за оставшееся короткое время:
Некоторые другие эксперименты
Точная арифметика в 64 битах
Замысел точной арифметики нельзя реализовать ни в наивных 64-битных рациональных числах, ни в 32-битных (1|5|26) рациональных числах с плавающей чертой дроби. А будут ли работать 64-битные числа с плавающей чертой дроби?
Я быстренько реализовал рациональные числа 1|6|57 (хоть и пришлось изучить новые внутренние механизмы x64 для сдвига битов). Эти 57 битов числителя/знаменателя позволили трассировать гораздо больший интервал расстояний. Мне и в самом деле удалось трассировать сцену с несколькими треугольниками со всей точной арифметикой (не упомянутую выше сцену с параллелограммами и глобальным освещением, а всего лишь несколько треугольников перед камерой). И меня ждал успех! Однако тест копланарности, который я реализовал для проверки корректности, требовал несколько операций скалярного и векторного произведения, которые заставляли числа начинать ренормализовать себя. Поэтому хоть я и знал, что рендер был точным, я не мог бы «доказать» это экспериментально. Какая ирония. В общем, это означает, что 64 бит было достаточно для нескольких треугольников, но более сложные сцены всё равно развалятся. Однако это заставило меня задуматься над другим вопросом: существует ли какой-нибудь алгоритм, который можно использовать для проверки копланарности, основанный не на абсолютных значениях, а на модульной арифметике? Наверно, в модульной арифметике рациональные числа не должны «взрываться» в размерах? У меня не было времени всё это исследовать, да я и не специалист в теории чисел.
Квадратные корни
В последний (второй) вечер исследований я решил ненадолго остановиться на этой теме и изучить новую информацию. Я хотел реализовать наилучшую возможную для рациональных чисел функцию квадратного корня. Моё текущее наивное решение (плохое) брало целочисленный квадратный корень от числителя (с соответствующим округлением), а затем делало то же самое со знаменателем. Так как квадратный корень дроби — это дробь квадратных корней числителя и знаменателя, в целом этот подход возвращает приличные результаты, не слишком отличающиеся от наилучшего ответа. Но он совершенно точно не возвращает наилучшую рациональную аппроксимацию квадратного корня рационального числа. Он выполняет вместо одного приближения два.
Я попробовал следующее: в конце концов, здесь мы ищем два целых числа x и y, такие, что
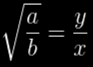
Тогда мы можем переписать это выражение как нахождение решения (нетривиального) следующего диофантова уравнения («диофантово» означает, что нас интересуют только целочисленные решения):
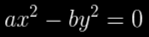
Проведя поиски в Википедии, я обнаружил, что конкретно это уравнение является так называемым «видоизменённым уравнением Пелля» (Modified Pell's equation). Существуют алгоритмы, находящие наименьшие значения x и y для решения этого уравнения. К сожалению, моё внимание быстро сместилось к другой любопытной диофантовой математике, и я не приступил к реализации ни одного из этих алгоритмов.
Более эффективное сокращение
В последние минуты вечера я задумался об исследовании идеи использования многочисленных членов, сочетающихся в сложных геометрических операторах, например, в векторном произведении. Допустим, первым компонентом векторного произведения было
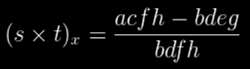
при допущении, что s.y=a/b, t.z=c/d, t.y=e/f, s.z=g/h
Это означало, что теперь я могу попробовать найти общие делители, например, между a и d, или e и h, и использовать их для предварительного сокращения.
У меня была ещё одна идея: если на каком-то этапе станет проблемой скорость рендеринга, то можно полностью отключить этапы поиска НОД и применять только нормализацию. Быстрая проверка показала, что в таком случае изображения рендеров всё равно остаются приемлемыми и хорошо работают с гораздо более высокой скоростью. Однако при этом мы, разумеется, получаем меньшее количество арифметически точных результатов.
В качестве компромисса можно отказаться от реализации процедуры или схемы НОД, и использовать вместо них что-то математически простое, жёстко прописанное в коде и эффективное, определяющее делимость только на 2, 3 и 5. Хоть так мы и не найдём исчерпывающее количество делителей, на практике это бы привело к нахождению большого количества сокращений. Задумайтесь — делимость на 2 встречается в три раза чаще, чем делимость на 7, и в 20 раз чаще, чем делимость на 41!
Заключение
После этого опыта я начал считать, что вполне возможно существование представления чисел, основанного на рациональных числах, похожего на то, что я называю «плавающей чертой дроби». Представление, совместимое с целыми числами и способное выполнять многие операции в точной арифметике для многих задач (при условии, что входящие данные представлены в рациональном виде). Большой потенциал имеет 64-битная версия (1|6|57), хотя и 32-битная версия (1|5|26) уже создаёт интересные рендеринги.
Если бы это был не эксперимент на два вечера, а что-то профессиональное, создаваемое в студии или компании, то в дальнейшем можно было бы сделать следующие шаги:
* Получить гистограмму количества точно и не точно трассированных пикселей (другими словами, частоты выполнения нормализации)
* Попробовать реализовать жёстко заданное сокращение на делители 2, 3 и 5 и измерить процент утерянных точных пикселей
* Показать разницу пикселей между рендерингом с плавающей запятой и рендерингом с плавающей чертой дроби
* Найти изобретательные способы применения неиспользуемых значений битового формата «плавающей черты дроби», например, для обозначения Inf и NaN
* Реализовать обнаружение NaN, Inf, underflow, overflow.
В целом, это было увлекательное исследование. В процессе я обнаружил несколько сюрпризов, придумал одно небольшое изобретение и много узнал об уравнении Пелля, квадратных корнях, НОД, внутренних механизмах x86_64, дзета-функции Римана и некоторых других аспектах. Я очень этим доволен!
Автор: PatientZero






