Зачем нужна низкоуровневая оптимизация на Эльбрусе или как ускорить распознающую систему в полтора раза

Встретив 2019 год и немного отдохнув от разработки новых фич для Smart IDReader, мы вспомнили, что давно ничего не писали об отечественных процессорах. Поэтому мы решили срочно исправиться и показать еще одну распознающую систему на Эльбрусе.

В качестве распознающей системы была рассмотрена система распознавания объектов живописи “в неконтролируемых условиях методом с обучением по одному примеру” [1]. Эта система строит описание изображения на основе особых точек и их дескрипторов, по которому выполняет поиск в индексированной базе картин. Мы проанализировали производительность данной системы и выделили наиболее времязатратную низкоуровневую часть алгоритма, который затем оптимизировали с помощью инструментов платформы Эльбрус.

О какой распознающей системе вообще идет речь?

В настоящее время в большинстве музеев и галерей используются различные инструменты для самостоятельного ознакомления с экспозицией. Наряду с классическими аудиогидами получили широкое распространение мобильные приложения, использующие методы обработки и анализа изображений. Некоторые из таких приложений распознают графические коды экспонатов (штриховые или QR) [2], для других [3-4] входными данными являются фото- или видео- кадры с экспонатом, снятым крупных планом (Smartify, Artbit). Разумеется, «мобильные гиды» последней категории удобнее для пользователя [5], чем решения с ручным вводом номера экспоната или распознаванием QR: номер и код достаточно малы, и их поиск и ввод требует дополнительных действий, не связанных с обзором экспозиции. Именно такую систему мы и будем рассматривать.

Задача распознавания произведений живописи на изображениях была сформулирована следующим образом. Изображение-запрос должно быть отнесено к одному из классов , где – класс изображений -го экспоната, при , – класс прочих изображений, соответствующий значению «неизвестная картина». Для каждого задано изображение-эталон .
Кроме того, мы руководствовались следующими предположениями:

1. Изображение-запрос получено с помощью камеры мобильного устройства неподготовленным пользователем во время экскурсии, следовательно:
   а) оно может содержать визуальные дефекты – блики, расфокусированные области, шум;
   б) ракурс, кадрирование, освещение и цветовой баланс неизвестны (Рис. 1а);
   в) на снимке могут присутствовать посторонние объекты, такие как декорации, картинные рамы, посетители (Рис. 1б).
2. Изображение-эталон представляет собой изображение высокого разрешения с фронтальной проекцией картины или ее цифровую репродукцию. Эталон не содержит посторонних объектов и визуальных дефектов. Эталонами могут служить, например, качественно отсканированные страницы художественных альбомов (Рис. 2).
3. Картина (как на запросе, так и на эталоне) может относиться к любому стилю – реализм,
   импрессионизм, абстракционизм, фрактальная графика и т.д.
4. Количество классов соответствует размеру коллекции и для одной галереи может достигать
   сотен тысяч экспонатов [6].

Рисунок 1 — Примеры изображений-запросов а) картина сфотографирована издали при слабом освещении, б) в кадре посетитель.

Рисунок 2 — Примеры изображений-эталонов для картин а) Клод Моне «De Voorzaan en de Westerhem», б) Сальвадор Дали «La persistència de la memòria»

Основная идея нашего решения этой задачи основана построении специального описания картины по входному изображению, которое затем используется для поиска этой картины в базе описаний эталонных изображений картин высокого разрешения, не подверженных геометрическим искажениям и иным фотодефектам. В качестве такого описания выступают координаты особых точек, найденных с помощью алгоритма YACIPE [7], и их RFD дескрипторы.

Для каждого эталона построим описание, а затем проиндексируем – для каждой точки в описании занесём запись вида в рандомизированное иерархическое кластеризующее поисковое дерево [8], которое позволяет выполнять приближенный поиск ближайших соседей с существенным выигрышем по скорости в сравнении с линейным поиском. В качестве метрики используется расстояние Хэмминга, поскольку мы используем бинарный дескриптор.

Процесс распознавания выглядит следующий образом:

1. На изображении-запросе зона картины предварительно локализуется с использованием предположения о прямоугольности рамы. Поиск зоны осуществляется с помощью быстрого алгоритма поиска четырёхугольников [9] со снятым ограничением на соотношение сторон. Это позволяет предотвратить следующие проблемы:
   – недостаточное описание области картины из-за посторонних объектов в кадре, на которых могут быть особые точки с наилучшими оценками;
   – вычислительные затраты на сопоставление дескрипторов областей, расположенных вне картины;
   – значимое несовпадение масштаба и угла наклона между эталоном в базе и изображением картины, что приводит к некорректному результату сопоставления дескрипторов.

2. Изображение в найденной зоне проективно нормализуется:

   

   где – проективное преобразование.

3. Выполняется построение компактного описания :
   а) изображение приводится к стандартному размеру с сохранением пропорций, чтобы сделать алгоритм более устойчивым к масштабированию;
   б) высокочастотный шум подавляется фильтром Гаусса;
   в) на полученном изображении вычисляются особые точки, их количество искусственно ограничивается до лучших по внутренней оценке YACIPE;
   г) вычисляются цветные RFD-подобные дескрипторы окрестностей найденных особых точек, поскольку в нашей задаче было важно сохранить информацию о цветовых признаках входных изображений. Например, картины на Рис. 3 было бы крайне сложно различить без нее;
   д) таким образом, описание изображения можно представить как: , где – координаты i-й особой точки, а – дескриптор окрестности i-й особой точки.

4. Для каждой записи в индексе производится аппроксимированный поиск ближайших соседей дескриптора . К найденным дескрипторам применяется процедура голосования – дескриптор добавляет голос эталону . Затем отбираются K эталонов-кандидатов с наибольшим количеством голосов.

5. Для каждого из выбранных вариантов с помощью алгоритма RANSAC выполняется поиск проективного преобразования , переводящего, в пределах заданной геометрической погрешности , точки запроса в точки эталона . Пара точек с близкими дескрипторами считается верным сопоставлением, если:

   

6. В качестве окончательного результата выбирается эталон , для которого число верных сопоставлений оказалось максимальным. Если оно меньше определённого порогового значения , результатом будет ответ «неизвестная картина», чтобы избежать ложных срабатываний (например, на картинах, для которых в поисковой базе нет описания эталона).

Рисунок 3 — Claude Monet. Rouen Cathedral, West Facade, Sunlight (слева) and Rouen Cathedral, Portal and Tower Saint-Romain in the Sun (справа).

Одной из основных частей системы является поиск близких дескрипторов с использованием расстояния Хэмминга в качестве метрики. Поскольку оно вычисляется много раз, этот этап становится достаточно вычислительно трудоемким и занимает 65% времени работы системы. Именно поэтому мы оптимизировали именно его.

Совсем небольшое описание архитектуры Эльбрус

Архитектура процессоров Эльбрус использует принцип широкого командного слова (Very Long Instruction Word, VLIW). Это означает, что процессор исполняет команды группами, причем внутри каждой группы отсутствуют зависимости и эти команды исполняются параллельно. Каждая такая группа называется широким командным словом. Формирование широких командных слов выполняет оптимизирующий компилятор, благодаря чему возможен более подробный анализ исходного кода, приводящий к более эффективному распараллеливанию [10].

Особенностью архитектуры Эльбрус являются методы работы с памятью. Помимо наличия кэша, позволяющего оптимизировать время доступа в память, процессоры Эльбрус поддерживают программно-аппаратный метод предварительной подкачки данных. Этот метод позволяет прогнозировать обращения в память и производить подкачку данных в буфер предварительной подкачки данных. Аппаратная часть процессора включает в себя специальное устройство для обращения к массивам (Array Access Unit, AAU), но необходимость подкачки определяется компилятором, который генерирует специальные инструкции для AAU. Использование устройства подкачки является более эффективным, чем помещение элементов массива в кэш, поскольку элементы массивов чаще всего обрабатываются последовательно и редко используются более одного раза [11]. Однако необходимо отметить, что использование буфера предварительной подкачки на Эльбрусе возможно только при работе с выровненными данными. Благодаря этому чтение/запись выровненных данных происходят заметно быстрее, чем соответствующие операции для невыровненных данных.

Кроме того, процессоры Эльбрус поддерживают несколько видов параллелизма помимо параллелизма на уровне команд: SIMD-параллелизм, параллелизм потоков управления, параллелизм задач в многомашинном комплексе. Особый интерес для нас представляет SIMD-параллелизм.

Особенности использования SIMD-расширения процессора Эльбрус

Использование SIMD-расширений может осуществляться в двух режимах: автоматическом и непосредственном. В первом случае распараллеливание операций полностью выполняется компилятором без участия разработчика. Этот режим ограничен, так как оптимизированный код должен полностью повторять поведение исходного кода, в том числе и поведения при переполнении, округлении и т.д. При этом поведение команд SIMD-расширения может отличаться в этих аспектах от команд процессора. Кроме того, алгоритмы, применяющиеся в компиляторах, несовершенны и не всегда способны выполнить эффективное распараллеливание. Однако также разработчики могут обращаться к командам SIMD-расширений непосредственно, используя интринсики. Интринсики – функции, вызовы которых заменяются компилятором на высокоэффективный код для данной платформы, в частности, на команды SIMD-расширения. Процессоры Эльбрус-4С и Эльбрус-8С поддерживают набор интринсиков, для которого размер регистра составляет 64 бита. Он включает в себя операции для преобразования данных, инициализации элементов вектора, арифметических операций, побитовых логических операций, перестановки элементов вектора и др.

При использовании интринсиков на платформе Эльбрус следует уделять особое внимание доступу в память, поскольку в практических задачах, например, задачах обработки изображений, часто требуется невыровненное чтение данных в 64-битный регистр. Такое чтение само по себе неэффективно, так как требует пары команд чтения и последующей команды формирования блока данных, но, что еще важнее, при этом не может использоваться буфер подкачки массивов, повышающий скорость доступа к данным. Однако стоит отметить, что проблема неэффективного доступа к невыровненным данным актуальна для процессоров Эльбрус-4С и Эльбрус-8С, в то время как для более нового Эльбрус-8СВ с 5 версией системы команд она частично решена. Ожидается, что процессорах Эльбрус с 6 версией системы команд она будет решена полностью.

Однако на процессорах Эльбрус-4С и Эльбрус-8С низкоуровневую обработку данных эффективно выполнять с учетом выравнивания. Например, для числовых массивов, она может состоять из нескольких этапов: обработка начальной части (до границы выравнивания на 64-бита одного из массивов), обработка основной части, использующая выровненный доступ к памяти, и обработка оставшихся элементов массива. Поскольку анализ указателей во время компиляции является нетривиальной задачей, можно использовать флаг компилятора –faligned, с которым все операции доступа к памяти выполняются выровненным образом.

Следующая особенность использования интринсиков на платформе Эльбрус связана непосредственно с его VLIW-архитектурой. Благодаря наличию нескольких арифметико-логических устройств (АЛУ), которые работают параллельно и загружаются при формировании широких командных слов, несколько команд могут исполняться одновременно. Всего в процессорах Эльбрус-4С и Эльбрус-8С шесть АЛУ, которые можно задействовать в рамках одной широкой команды, однако каждое АЛУ поддерживает свой набор интринсиков. Простые операции, например, сложение или умножение элементов в 64-битных регистрах, как правило поддерживают два АЛУ. Это означает, что процессор Эльбрус может исполнить по две таких инструкции за один такт. Для этого в исполняемом коде следует использовать развертывание циклов. Оптимизирующий компилятор для платформы Эльбрус поддерживает прагму #pragma unroll(n), которая позволяет выполнить развертывание n итераций цикла.

Пример реализации функции сложения с учетом этих особенностей можно посмотреть в нашей предыдущей статье.

Эксперименты

Ура, текст кончился и наконец-то мы что-то запустим на Эльбрусе!

Сначала рассмотрим отдельно расстояние Хэмминга. Не мудрствуя лукаво, мы сравнивали два битовых вектора случайных данных. Двоичные значения были упакованы в массивы 8-битных целых чисел, причем для простоты мы считали, что длины исходных векторов кратны 8. Как обычно код написан на С++, компилировался lcc 1.21.24 – оптимизирующим эльбрусным компилятором.

Мы написали несколько реализаций расстояния Хэмминга, которые последовательно учитывали особенности процессоров Эльбрус. Они выглядели следующим образом:

1. Используется побитовый XOR между 8-битными целыми числами и таблица предподсчитанных значений. Это базовая реализация без интрисиков и прочих хитростей.
2. Используется XOR между 32-битными целыми числами и интринсик для вычисления числа единиц в 32-битном целом числе — popcnt32. Выравнивания данных по границе в 32-бита не выполнялось.
3. Используется XOR между 64-битными целыми числами и интринсик для вычисления числа единиц в 64-битном целом числе — popcnt64. Выравнивания данных по границе в 64-бита не выполнялось.
4. Используется XOR между 64-битными целыми числами и интринсик для вычисления числа единиц в 64-битном целом числе — popcnt64. Доступ в память осуществляется выровненным образом. Поскольку начальные адреса массивов могут иметь разное выравнивание, при чтении одного из массивов выполняется чтение двух соседних 64-битных блоков и формирование из них необходимого 64-битного блока.
5. Используется XOR между 64-битными целыми числами и интринсик для вычисления числа единиц в 64-битном целом числе — popcnt64. Доступ в память осуществляется выровненным образом. Поскольку начальные адреса массивов могут иметь разное выравнивание, при чтении одного из массивов выполняется чтение двух соседних 64-битных блоков и формирование из них необходимого 64-битного блока. Дополнительно использован флаг компилятора -faligned.
6. Используется XOR между 64-битными целыми числами и интринсик для вычисления числа единиц в 64-битном целом числе — popcnt64. Доступ в память осуществляется выровненным образом. Поскольку начальные адреса массивов могут иметь разное выравнивание, при чтении одного из массивов выполняется чтение двух соседних 64-битных блоков и формирование из них необходимого 64-битного блока. Дополнительно использован флаг компилятора -faligned и прагмы компилятора #pragma unroll(2) (чтобы использовать для вычисления popcnt64 оба доступных АЛУ) и #pragma loop count(1000) (чтобы включить дополнительные цикловые оптимизации).

Результаты замеров времени приведены в таблице 1.

Таблица 1. Время вычисления расстояния Хэмминга между двумя массивами упакованных двоичных чисел длины 10^5 на машине с процессором Эльбрус-4С. Выполнено усреднение времени по 10^5 запускам.

№	Эксперимент	Время, мс
1	таблица предподсчитанных значений	141.18
2	popcnt32, без выравнивания	125.54
3	popcnt64, без выравнивания	58.00
4	popcnt64, выравнивание	17.36
5	popcnt64, выравнивание, -faligned	17.15
6	popcnt64, выравнивание, -faligned, pragma unroll	12.23

Можно видеть, что все рассмотренные оптимизации привели к снижению времени работы в 11,5 раз. При этом стоит отметить, что использование интринсиков при невыровненном доступе в память показало ускорение лишь в 1,13 раза (для popcnt32) и в 2,4 раза (для popcnt64), в то время как учет выравнивания данных привел к использованию буфера подкачки массивов APB, с помощью которого удалось достичь ускорения еще в 3,4 раза (58 мс против 17,15 мс). Несмотря на то, что в рассмотренном примере использование флага -faligned не показало значительного прироста производительности, в более сложных алгоритмах возможна ситуация, когда компилятор не сможет проанализировать исходный код достаточно глубоко, чтобы сгенерировать команды для APB. Учет актуального количества специализированных AЛУ позволил ускорить вычисления еще в 1,4 раза.

Неплохо так получилось! Поскольку мы сравнивали аж 6 вариантов реализации, приведем псевдокод финального, самого быстрого:

Вход: массивы 8-битных целых чисел A и B, массив T, где T[i] содержит число единиц в числе i
Выход: целое число res, равное расстоянию Хэмминга между A и B

offset ← число байтов до границы выравнивания массива A на 64-бита
effective_len ← максимальная длина массива, которую можно обработать блоками по 64-бита
for i from 1 to offset:
  res ← res + T[xor(A[i] , B[i])]

v_a ← 64-битный блок данных, начиная с A[offset+1]
v_b1 ← 64-битный блок данных, включающий элемент B[offset]
v_b2 ← 64-битный блок данных, следующий за v_b1
//включение развертывания цикла и цикловых оптимизаций для всех 64-битных блоков данных
for i from offset to effective_len:
  v_b ← align(v_b1, v_b2) // создание 64-битного блока данных, соответствующего v_a
  res ← res + popcnt64(xor(v_a, v_b))
  v_a ← следующий 64-битный блок данных
  v_b1 ← v_b2
  v_b2 ← следующий 64-битный блок данных

// Обработать оставшиеся элементы массивов

Было бы здорово раз и навсегда ускорить вычисление расстояния Хэмминга в 11,5 раз, однако в жизни все немного сложнее: подобная реализация будет иметь преимущество лишь при достаточно больших длинах массивов. На Рис. 4 представлено сравнение времени подсчета с использованием таблицы предподсчитанных значений и нашей финальной реализации. Можно видеть, что при наша версия начинает выигрывать только начиная с длин, превышающих 400 байт, и это тоже необходимо учитывать при оптимизации на Эльбрусе.

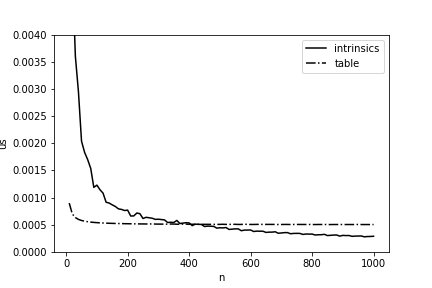
Рисунок 4 — Среднее время (на 1 байт) вычисления расстояния Хэмминга между двумя массивами в зависимости от их длины на Эльбрус-4С.

Ну все, теперь мы готовы к замерам времени работы всей системы. Мы измерили среднее время обработки запроса (без учета загрузки изображения) для 933 запросов. При составлении компактного описания изображения использовался цветной RFD-подобный бинарный дескриптор длиной 5328 бит. Он состоял из 3 конкатенированных 1776-битных серых RFD-дескрипторов, вычисленных для каждого канала участка входного изображения. С одной стороны, такие длинные дескрипторы не радуют высокой скоростью вычисления и сравнения, с другой стороны — позволяют обеспечить достаточно высокое качество работы. Однако есть и хорошие новости — мы можем применить быструю реализацию расстояния Хэмминга для их сравнения! Длины сравниваемых массивов равны 666 байт, что больше порогового значения в 400 байт для Эльбрус-4С.

Результаты замеров приведены в Таблице 2. Можно видеть, что одна только быстрая реализация расстояния Хэмминга дает ускорение обработки запроса в 1,5 раза. Стоит также отметить, что эта оптимизация никак не меняет результаты вычислений, а значит и качество распознавания.

Таблица 2. Среднее время обработки запроса к системе распознавания объектов живописи в неконтролируемых условиях.

Эксперимент	Время запроса, с	Вычисление расстояния Хэмминга заняло	Ускорение, разы
Базовая реализация	2.81	63%	-
Быстрая реализация	1.87	40%	1.5

Заключение

В данной статье мы немного рассказали об устройстве системы распознавания объектов живописи в неконтролируемых условиях и в очередной раз показали как низкоуровневые манипуляции могут значительно повысить ее быстродействие на платформе Эльбрус. Так, предложенная реализация расстояния Хэмминга, работает на порядок (!) быстрее, чем реализация с помощью таблицы предподсчитанных значений при достаточно большой длине входных векторов, а вся система ускорилась в полтора раза! Для достижения такого результата были использованы SIMD-расширения, а также учтены особенности архитектуры и доступа в память процессоров Эльбрус-4С и Эльбрус-8С. Эти результаты показывают, что процессоры Эльбрус содержат значительные ресурсы для эффективной работы, которые не задействуются полностью при отсутствии специально выполненной оптимизации. Однако ожидается, что на более новых процессорах Эльбрус будут усовершенствованы методы доступа в память, что позволит выполнять часть подобных оптимизаций в автоматическом режиме и значительно облегчит жизнь разработчикам.

Литература

[1] Н.С. Скорюкина, А.Н. Миловзоров, Д.В. Полевой, В.В. Арлазаров. Метод распознавания объектов живописи в неконтролируемых условиях с обучением по одному примеру // Труды ИСА РАН. — Спецвыпуск, 2018 г. — с. 5-15.
[2] Pérez-Sanagustín M. et al. Using QR codes to increase user engagement in museum-like spaces //Computers in Human Behavior. – 2016. – Т. 60. – С. 73-85. doi: 10.1016/j.chb.2016.02.012
[3] Антощук С. Г., Годовиченко Н. А. Анализ точечных особенностей изображения в системе «Мобильный виртуальный гид» // Pratsi. – 2013. – №. 1 (40). – С. 67-72.
[4] Andreatta C., Leonardi F. Appearance based paintings recognition for a mobile museum guide //International Conference on Computer Vision Theory and Applications, VISAPP. – 2006.
[5] Leonard Wein. 2014. Visual recognition in museum guide apps: do visitors want it?.. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI '14). ACM, New York, NY, USA, 635-638.
doi: 10.1145/2556288.2557270
[6] Третьяковская галерея, https://www.tretyakovgallery.ru/collection/
[7] Лукоянов А. С., Николаев Д. П., Коноваленко И. А. Модификация алгоритма YAPE для изображений с большим разбросом локального контраста // Информационные технологии и нанотехнологии. – 2018. – С. 1193-1204.
[8] Muja M., Lowe D. G. Fast matching of binary features //Computer and Robot Vision (CRV), 2012 Ninth Conference on. – IEEE, 2012. – С. 404-410.
doi: 10.1109/CRV.2012.60
[9] Skoryukina, N., Nikolaev, D. P., Sheshkus, A., Polevoy, D. (2015, February). Real time rectangular document detection on mobile devices. In Seventh International Conference on Machine Vision (ICMV 2014) (Vol. 9445, p. 94452A). International Society for Optics and Photonics.
doi: 10.1117/12.2181377
[10] Ким А.К., Бычков И.Н. и др. Российские технологии “Эльбрус” для персональных компьютеров, серверов и суперкомпьютеров // Современные информационные технологии и ИТ-образование, М.: Фонд содействия развитию интернет-медиа, ИТ-образования, человеческого потенциала «Лига интернет-медиа», 2014, No 10, с. 39-50.
[11] Ким А.К., Перекатов В.И., Ермаков С.Г. Микропроцессоры и вычислительные комплексы
семейства «Эльбрус». — СПб.: Питер, 2013. — 272 С.

Автор: SmartEngines

Источник