«2048» через несколько недель исполняется 5 лет, а значит, пора написать что-нибудь, посвящённое этой замечательной игре.
Особенно познавательна тема самостоятельной игры искусственного интеллекта в головоломку. Способы реализации есть самые разные и сегодня разберём относительно лёгкий из них. А именно — научим компьютерный разум собирать степени двойки с помощью метода Монте-Карло.
Вдохновением к данному труду послужило обсуждение на stackoverflow, где умные ребята предложили действенные способы компьютерной игры. По всей видимости, наилучшим способом является метод минимакса с альфа-бета отсечением и через пару дней ему будет посвящена следующая публикация.
Казино-способ предложен пользователем stackoverflow ![]() Ronenz в рамках вышеупомянутого обсуждения. Весь следующий раздел — это перевод с его публикации.
Ronenz в рамках вышеупомянутого обсуждения. Весь следующий раздел — это перевод с его публикации.
Метод Монте-Карло
Я заинтересовался идеей ИИ для этой игры, в которой нет жестко запрограммированного интеллекта (то есть отсутствуют эвристики, подсчет очков и т.п.). ИИ должен «знать» только правила игры и «разбираться» в игре. Это отличает его от большинства ИИ (таких, как в этой теме), поскольку игровой процесс, фактически, является грубой силой, управляемой функцией подсчета очков, отражающей человеческое понимание игры.
ИИ алгоритм
Я обнаружил простой, но удивительно хороший игровой алгоритм: чтобы определить следующий ход для данного состояния поля, ИИ разыгрывает в игру в оперативной памяти, делая случайные ходы до тех пор, пока игра не закончится поражением. Это делается несколько раз, при этом отслеживается конечный счет. Затем рассчитывается средний конечный балл с учётом начального хода. В качестве уже реально выбираемого хода выбирается тот начальный ход, который показал наибольший средний результат.
При 100 прогонах (т.е. не в реальной игре, а в расчётной игре в оперативной памяти) для каждого начального ход ИИ добирается до плитки 2048 в 80% случаев и плитки 4096 в 50% случаев. При использовании 10000 прогонов 2048 получается в 100% случаев, 70% — для 4096 и около 1% — для 8192.
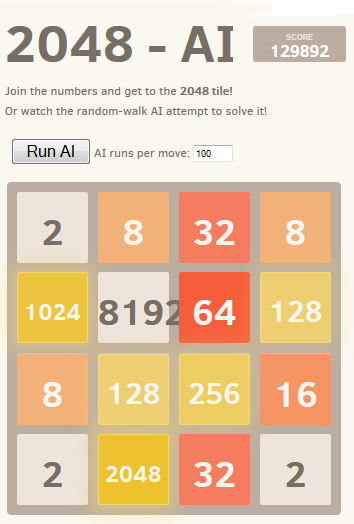
Посмотреть в действии
Лучший достигнутый результат показан на скриншоте:
Интересным фактом для данного алгоритма является то, что хотя игры с произвольно осуществляемыми ходами ожидаемо довольно плохи, тем не менее выбор лучшего (или наименее плохого, если угодно) хода приводит к очень хорошему игровому процессу: типичная игра ИИ методом Монте-Карло может набрать 70000 очков за 3000 ходов, однако игры с произвольной игрой в памяти из любой заданной позиции дают в среднем 340 дополнительных очка примерно за 40 дополнительных ходов перед проигрышем. (Вы можете убедиться в этом сами, запустив ИИ и открыв консоль отладки.)
Данный график иллюстрирует эту концепцию: синяя линия показывает счет игры после каждого хода. Красная линия показывает лучший результат алгоритма, произвольно делающий ходы с данной позиции до конца игры. По сути, красные значения «подтягивают» синие вверх, поскольку они являются наилучшими предложениями алгоритма. Интересно, что красная линия чуть-чуть выше синей линии в каждой точке, но синяя линия сокращает разрыв все больше и больше.
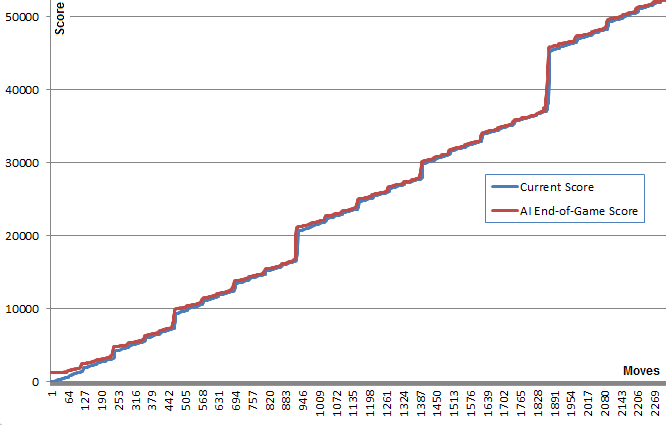
Я нахожу довольно удивительным, что алгоритм на самом деле необязательно предвидит хороший игровой процесс, и тем не менее выбирает ходы, которые его (хороший процесс) производят.
Позже я обнаружил, что этот метод может быть классифицирован как алгоритм поиска по дереву Монте-Карло.
Имплементация и ссылки
Сначала я создал версию на JavaScript, которую можно увидеть в действии здесь. Эта версия способна запустить 100 прогонов за приемлемое время. Откройте консоль для дополнительной информации. (исходники)
Позже, чтобы поиграться, я использовал высокооптимизированную инфраструктуру @nneonneo и реализовал свою версию на C++. Эта версия допускает до 100000 пробежек за ход и даже 1000000, если Вы готовы подождать. Инструкция по сборке прилагается. Всё работает в консоли, а также имеет пульт дистанционного управления для воспроизведения в веб-версии. (исходники)
Результаты
Удивительно, но увеличение количества прогонов кардинально не улучшает игровой процесс. Кажется, что у этой стратегии есть предел в 80000 пунктов с плиткой 4096 и всеми меньшими результатами, очень близкими к достижению плитки 8192. Увеличение количества прогонов со 100 до 100000 увеличивает шансы на достижение этого лимита (с 5% до 40%), но не преодолевает его.
Выполнение 10000 прогонов с временным увеличением до 1000000 вблизи критических позиций позволило преодолеть этот барьер менее чем в 1% случаев с достижением максимального количества набранных очков 129892 и плитки 8192.
Улучшения и оптимизации
После реализации этого алгоритма я попробовал много улучшений, включая использование минимальных или максимальных оценок или комбинации минимальных, максимальных и средних значений. Я также пытался использовать глубину: вместо того, чтобы пытаться выполнить K прогонов за ход, я пробовал K ходов за список ходов заданной длины (например, «вверх, вверх, влево») и выбирал первый ход из списка ходов с лучшим выигрышем.
Позже я реализовал дерево подсчета очков, которое учитывало условную вероятность того, что он сможет выполнить ход после заданного списка ходов.
Однако ни одна из этих идей не показала реального преимущества перед простой первой идеей. Я оставил закомментироанный код для этих идей в исходниках C++.
Я добавил механизм «Глубокий поиск», который временно увеличивал число прогонов до 1000000, когда любой из прогонов сумел случайно достичь следующей наивысшей плитки. Это привело к улучшению по временным показателям.
Мне было бы интересно узнать, есть ли у кого-нибудь другие идеи по улучшению, которые поддерживают независимость ИИ от предметной области?
Варианты и клоны 2048
Ради интереса, я также реализовал AI в виде букмарклета, подключив его к элементам управления игры. Это позволяет ИИ работать как с оригинальной игрой, так и со многими ее вариациями.
Это возможно благодаря доменно-независимой природе ИИ. Некоторые из вариантов довольно оригинальны, такие как гексагональный клон.
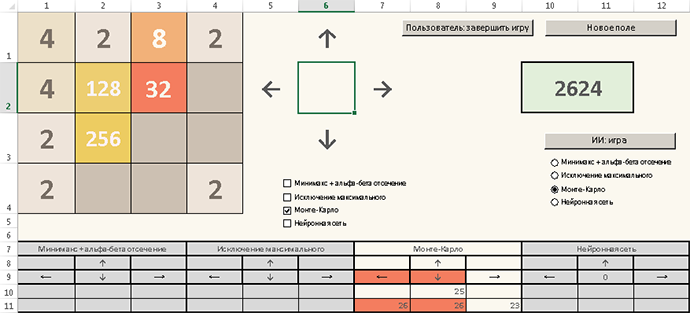
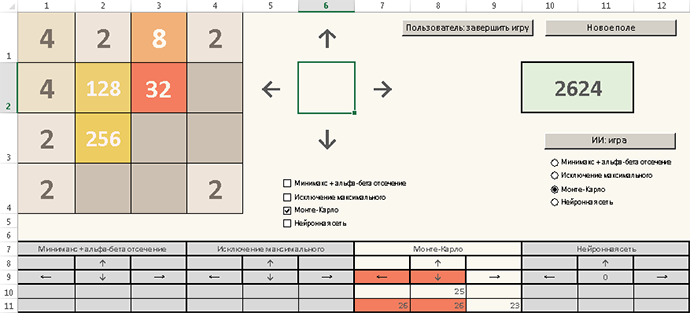
| На этом перевод завершён, но не только ради него затеяна данная публикация. До коликов захотелось самому проверить различные идеи для ИИ в 2048. С этой целью реализовал игру в Excel, написав приложение с макросами. Сама по себя реализация на VBA подвигом не является — погуглив, можно быстро обнаружить с дюжину различных эксцельных поделок. А вот не только состряпать 2048 в виде электронных таблиц, но и реализовать компьютерную самостоятельную игру — этого мне пока на глаза не попадалось. |
2048.xlsm
Само Excel-приложение можно скачать с гугл-диска.
Картинка кликабельна — откроется полноформатное изображение.
Кратко по интерфейсу и функционалу приложения.
Чтобы начать играть, нужно нажать на кнопку "Пользователь: начать игру". При повторных нажатиях на эту кнопку надпись меняется с "Пользователь: начать игру" на "Пользователь: завершить игру" и обратно, то есть в любой момент можно останавливать игру и затем запускать её снова. При остановке игры можно вручную поменять расклад на поле, улучшив или ухудшив свою позицию в целях тестирования или проверки каких-то идей.
Во время непосредственно игры можно делать ходы двумя способами:
- Клавиатурно: просто нажимая клавиши «вверх», «вниз», «влево», «вправо».
- С помощью мыши: щёлкая по клеткам с большими стрелочками, указывающими на нужное направление.
Кнопка "Новое поле" очищает игровое поле и на нём в случайном порядке размещает «двойку» и «четвёрку».
Самое интересное — метод Монте-Карло удалось реализовать, именно в том виде, в каком его предложил чувак со stackoverflow. На каждой позиции компьютер в памяти перебирает случайные ответвления для каждого первого хода («вверх», «вниз», «влево», «вправо») до тех пор пока это не приведёт к проигрышу. Статистически самое выгодное направление подсвечивается красным цветом в специальной таблице внизу. Можно использовать как подсказку, если видите что Ваша собственная игра заходит в тупик и нужно как-то спасаться. ;)
Над таблицей находятся чекбоксы с вариантами анализа. На данный момент решён только Монте-Карло, остальные будут добавлены в ближайшие дни (по итогам чего будут ещё хабрастатьи с обновлением excel-приложения и пояснениями по теории).
Также есть кнопка "ИИ: игра". Щёлкнув по ней, компьютерный помошник сделает один ход в соответствии с методом Монте-Карло или каким-то другим, который выбран в группе переключателей (минимакс и нейронная сеть будут в этом списке работать чуть позже).