
Примерно в течение месяца я решал одну из самых сложных технических проблем моей новой игры Dicey Dungeons — совершенствол ИИ для финального релиза игры. Это была довольно интересная работа, и многое в ней стало для меня новым, поэтому я решил немного о ней написать.
Для начала объясню: я не специалист в теории вычислительных машин, а просто один из тех, кто достаточно изучил программирование, чтобы создавать видеоигры, после чего закончил обучение, ухватив только то, что мне было необходимо. Обычно я могу решать свои задачи самостоятельно, но настоящий программист скорее всего не одобрил бы мои решения.
Я постарался написать статью на достаточно высоком уровне абстракции, чтобы основные идеи были понятны даже непрограммистам. Но я не эксперт в таких вещах, поэтому мои объяснения теории могут быть ошибочными. Напишите мне об этом в комментариях к оригиналу, я с радостью внесу изменения!
Ну, давайте начнём с объяснения задачи!
Задача
На случай, если вы не играли в Dicey Dungeons, вкратце расскажу об игре: это RPG с построением колоды (deckbuilding), в которой у каждого врага есть набор карт вооружений, выполняющих различные действия. Кроме того, они бросают кубики! Затем они помещают эти кубики на вооружение, чтобы нанести урон, или создавать различные статусные эффекты, или лечиться, или защищаться от урона, и тому подобное. Вот простой пример того, как маленькая лягушка использует большой меч и малый щит:

Более сложный пример: у этого Мастера на все руки есть гаечный ключ (spanner), позволяющий сложить два кубика вместе (то есть 3 + 2 дадут 5, а 4 + 5 дадут 6 и 3). Также у него есть молоток (Hammer), который накладывает на игрока эффект «шока», если применить к нему шестёрку, и трубка для стрельбы горохом (Pea Shooter), которая наносит мало урона, но зато у неё есть «обратный отсчёт», то есть она действует несколько ходов.

Ещё одно важное усложнение: в игре есть статусные эффекты, изменяющие возможности противников. Самые важные из них — это шок (Shock), который случайным образом отключает вооружение; шок можно снять, использовав на него дополнительный кубик, и «горение» (Burn), которое поджигает кубики. Пока кубики горят, ими можно пользоваться, но каждое использование будет стоить 2 очка здоровья. Вот, что делает умный Мастер на все руки, когда я накладываю шок и горение на всё его вооружение и кубики:

Разумеется, в игре есть и многое другое, но чтобы получить общее представление, этого достаточно.
Итак, наша задача: как заставить ИИ выбрать лучшее действие для своего хода? Как ему узнать, какой из горящих кубиков потушить, какой кубик использовать для снятия шока, а какой сохранить для важного вооружения?
Как он поступал раньше
Долгое время ИИ в Dicey Dungeons имел всего одно правило: он смотрел на всё вооружение слева направо, определял наилучший кубик, который на него можно было использовать, а затем использовал его. Это работало замечательно, но бывали и исключения. Поэтому я добавил новые правила.
Например, я справлялся с шоком, глядя на всё не подверженное шоку вооружение, и выбирая, какой бы кубик я использовал на нём, когда шок был бы снят, а потом помечал этот кубик как «зарезервированный» на будущее. С горящими кубиками я работал так: проверял, достаточно ли у меня здоровья, чтобы их потушить, и случайным образом выбирал, нужно ли это делать.
Я добавлял правило за правилом для всего, что мог вообразить, и в результате получил ИИ, который вроде бы работал! На самом деле удивительно, насколько хорошо показывало себя это переплетение разных правил — ИИ в Dicey Dungeons может быть и не всегда принимал верное решение, но оно всегда было хотя бы приемлемым. По крайней мере, для игры, всё ещё находящейся в разработке.
Но со временем система постоянного добавления новых правил начала трещать по швам. Люди обнаруживали эксплойты, заставлявшие ИИ вести себя глупо. Например, при правильном подходе можно было обхитрить одного из боссов так, чтобы он ни разу не атаковал игрока. Чем больше правил я добавлял для исправления ситуации, тем более странные вещи начинали твориться — одни правила вступали в противоречие с другими, стали проявляться граничные случаи.
Разумеется один из способов решения заключался в добавлении новых правил, рассмотрении каждой задачи одна за одной и создании новых конструкций if для их обработки. Но думаю, что таким образом я просто отодвигал истинное решение задачи. Ограничение системы заключалось в том, что её волновал только один вопрос: «Каким будет мой следующий ход?». Она никогда не заглядывала вперёд и не пыталась предположить, что может получиться из конкретной умной комбинации.
Поэтому я решил начать заново.
Классическое решение
Попробуйте поискать информацию об ИИ для игр, и скорее всего первым делом вы натолкнётесь на классическое решение — создание алгоритма минимакс. Вот видео о том, как он применяется при разработке ИИ для шахмат:
Реализация минимакса выглядит следующим образом:
Сначала создаём простейшую, абстрактную версию нашей игры, в которой есть вся необходимая информация для конкретного момента времени в игре. Мы назовём это доской. В случае шахмат это текущие позиции всех фигур. В случае Dicey Dungeons это список кубиков, вооружения и статусных эффектов.
Затем мы создаём функцию ценности, измеряющую, насколько хорошо идёт игра для конкретной конфигурации игры, то есть для конкретной доски. Допустим, в шахматах доска, на которой фигуры расположены в своих исходных позициях, оценивается в 0 очков. Доска, на которой вы съели пешку противника, имеет ценность 1 очков, а доска, на которой вы потеряли собственную пешку — ценность -1 очков. А доска, на которой мы поставили противнику мат, будет оцениваться в бесконечное количество очков, или что-то вроде этого!
Затем, из этой абстрактной доски мы симулируем все возможные ходы, которые можем сделать, что даёт нам новые абстрактные доски. Затем мы симулируем совершение всех возможных ходов на этих досках, и так далее, столько шагов, сколько вам захочется. Вот превосходная иллюстрация подобного решения с сайта freecodecamp.org:

Мы создаём граф всех возможных ходов, которые могут совершить оба игрока, и применяем к нему функцию ценности для оценки того, как идёт игра.
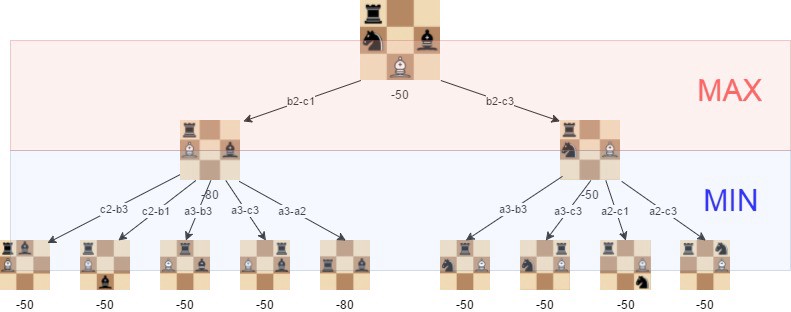
И в этом Dicey Dungeons отличается от минимакса: минимакс пришёл из математической теории игр, он предназначен для нахождения наилучшей серии ходов в мире, где противник стремится максимизировать свой счёт. Алгоритм называется так, потому что он занимается минимизацией потерь игрока, когда противник играет, чтобы максимизировать свой выигрыш.
Но что происходит в Dicey Dungeons? На самом деле меня не волнует, что делает мой противник. Чтобы игра была увлекательной, искусственному интеллекту достаточно делать логичные ходы — определять наилучший способ применения кубиков к вооружению, чтобы бой был честным. Другими словами, мне важен только «макс», без «мини».
То есть, чтобы ИИ Dicey Dungeons совершал хороший ход, мне достаточно создать этот граф возможных ходов и найти доску, имеющую наибольшую оценку, а затем сделать ходы, ведущие к этой точке.
Простой ход противника
Ну, перейдём к примерам! Давайте снова рассмотрим лягушку. Как ей решить, что делать дальше? Как она узнает, что выбранное действие является наилучшим?

По сути, у неё есть всего два варианта. Поместить 1 на широкий меч, а 3 на щит, или сделать наоборот. Она очевидно решает, что лучше положить на меч 3, а не 1. Но почему? Потому что она изучила все возможные результаты:
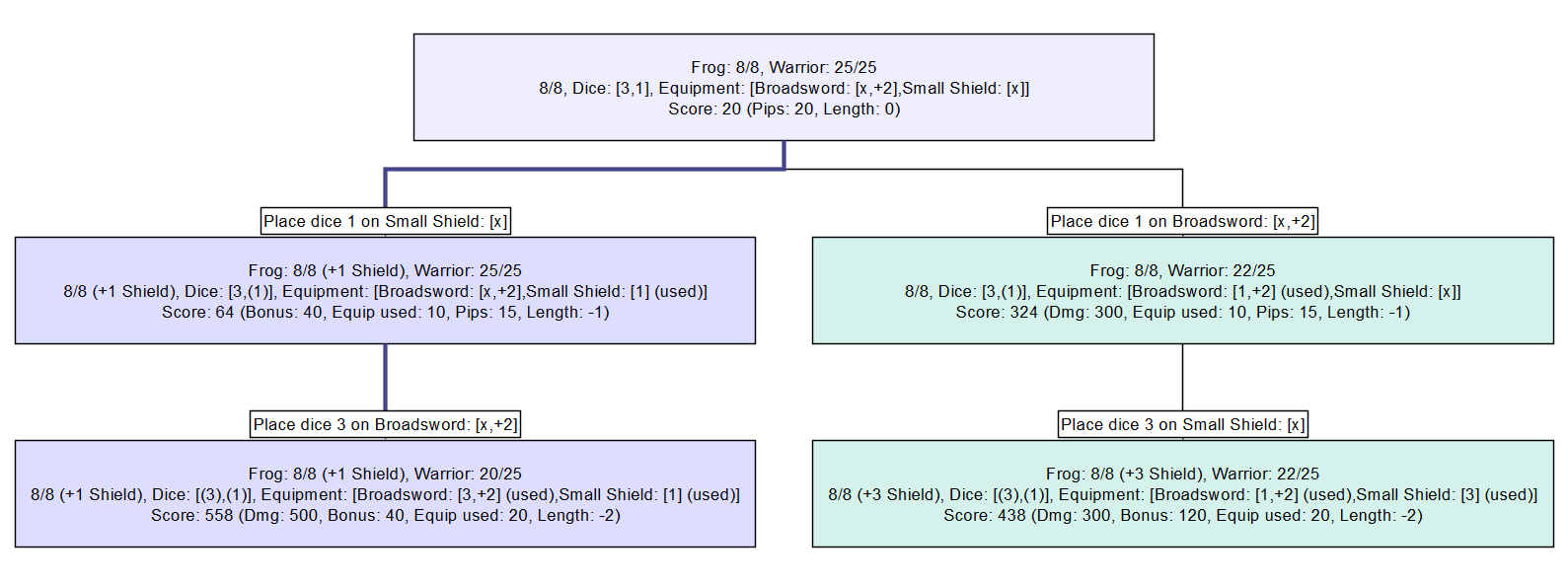
Если положить на меч 1, то мы получим 438 очков. Если положить на него 3, то получим 558 очков. Замечательно! Значит, я получаю больше очков, помещая на меч 3, задача решена.
Откуда берутся эти очки? Система оценки в Dicey Dungeons на данный момент учитывает следующие аспекты:
- Урон: самый важный фактор — 100 очков за каждое очко наносимого урона.
- Яд: важный статусный эффект, который ИИ считает почти столь же важным, как урон — 90 за каждый яд.
- Создание других статусных эффектов: например шока, горения, ослабления и т.д. Каждый из них стоит 50 очков.
- Бонусные статусные эффекты: добавление к самому игроку положительных статусных эффектов, таких как защита и тому подобное, стоит по 40 очков каждое.
- Использование вооружения: использование любого из видов вооружений стоит 10 очков, потому что если ничего другого не удалось, ИИ просто должен пытаться использовать всё.
- Снижение обратного отсчёта: для активации некоторых видов вооружения (например, для Pea Shooter) просто достаточно общей суммы на кубиках. Поэтому ИИ получает по 10 очков за каждое уменьшенное им очко обратного отсчёта.
- Точки на кубиках: ИИ получает 5 очков за каждую неиспользованную точку на кубике, то есть 1 стоит 5 очков, а 6 — 30 очков. Это сделано для того, чтобы ИИ предпочитал не использовать кубики, которые использовать не нужно, благодаря чему его ходы становятся очень похожими на человеческие.
- Длительность: ИИ теряет по 1 очку за ход, поэтому долгие ходы имеют чуть меньшую ценность, чем короткие. Это сделано для того, чтобы при наличии двух ходов, во всём остальном имеющих одинаковую ценность, ИИ выбирал самый короткий.
- Лечение: стоит всего 1 очко за одно восстановленное очко здоровья, потому что хоть я и хочу, чтобы ИИ считал это важным, но не очень следил за здоровьем. Всегда есть дела и поважнее!
- Бонусные очки: их можно добавлять к любому ходу, чтобы заставить ИИ делать что-то, чего бы он в противном случае никогда не совершил. Используется очень умеренно.
И наконец, есть два особых случая — если у атакуемой цели кончается здоровье, то это стоит миллион очков. Если здоровье заканчивается у ИИ, то это стоит минус миллион очков. Это значит, что ИИ никогда случайно себя не убьёт (допустим, погасив кубик при очень низком здоровье), или никогда не пропустит ход, в котором может убить игрока.
Эти числа неидеальны — возьмём, например, текущие открытые issues: 640, 642, 649, но это не очень важно. Даже приблизительно точных чисел достаточно, чтобы стимулировать ИИ поступать более-менее правильно.
Более сложные ходы врага
Случай с лягушкой настолько прост, что даже мой ужасный код может вычислить все варианты всего за 0,017 секунды. Но потом ситуация становится сложнее. Давайте снова взглянем на пример с Мастером на все руки.

Его дерево решений «немного» сложнее:
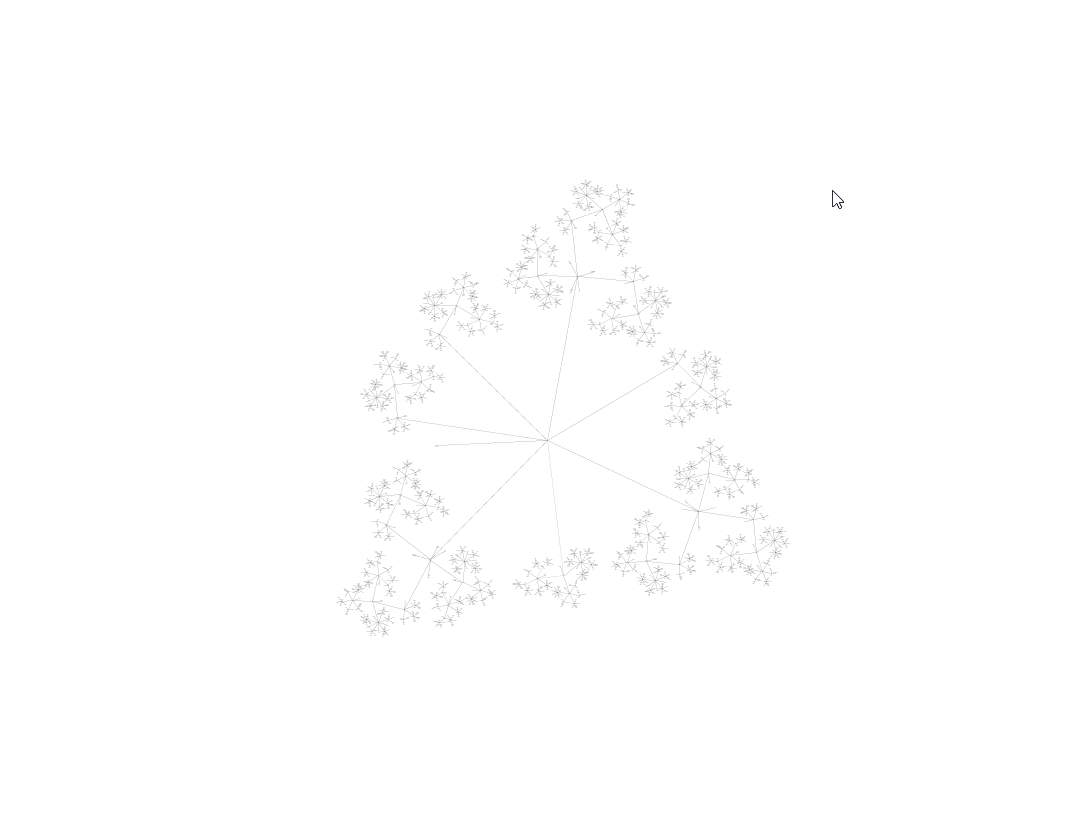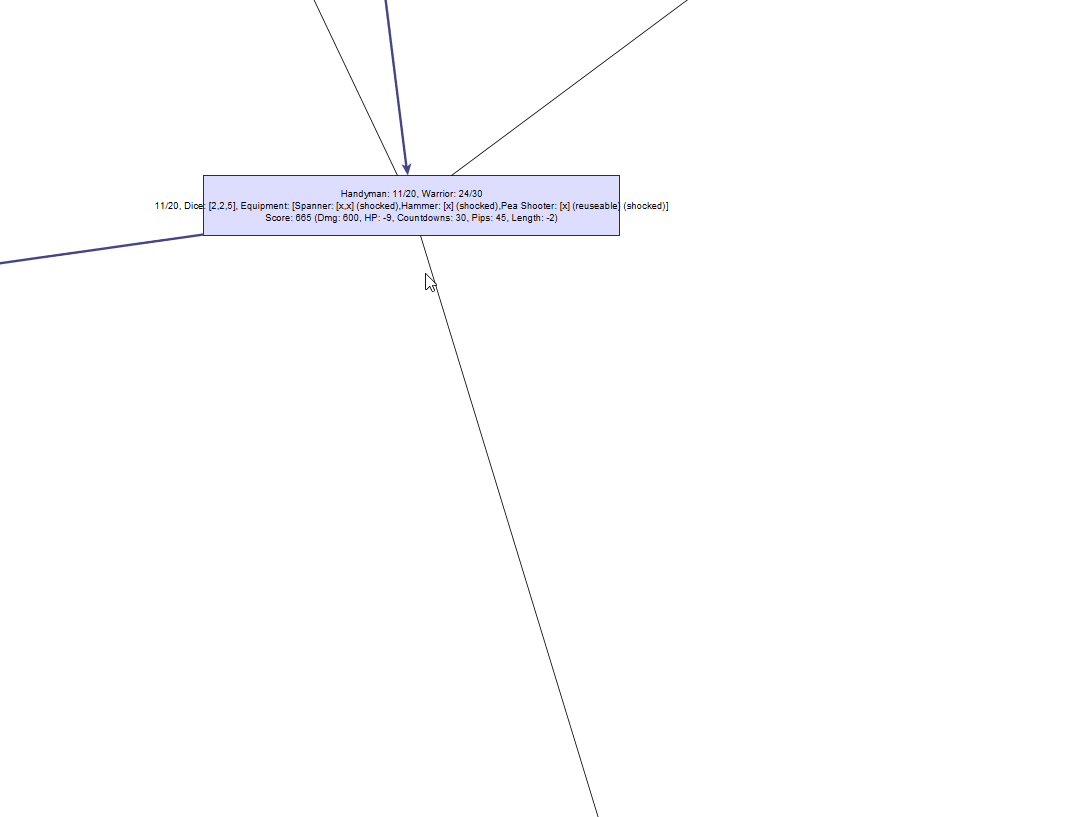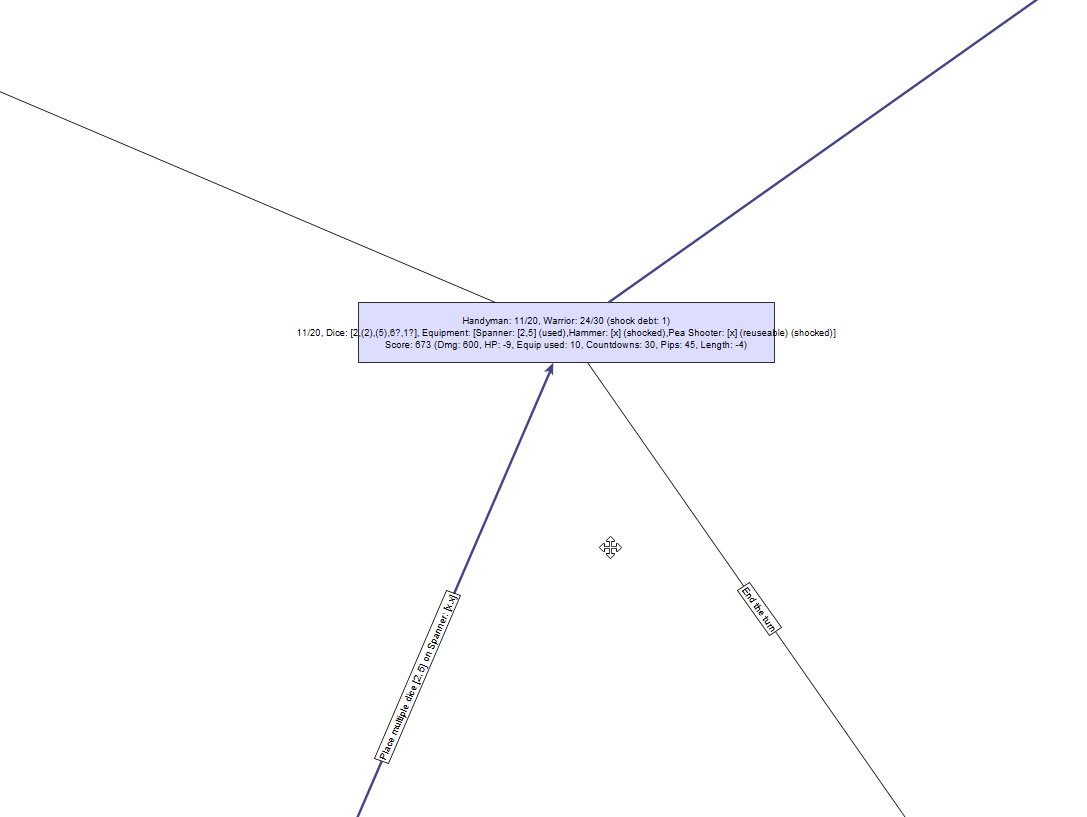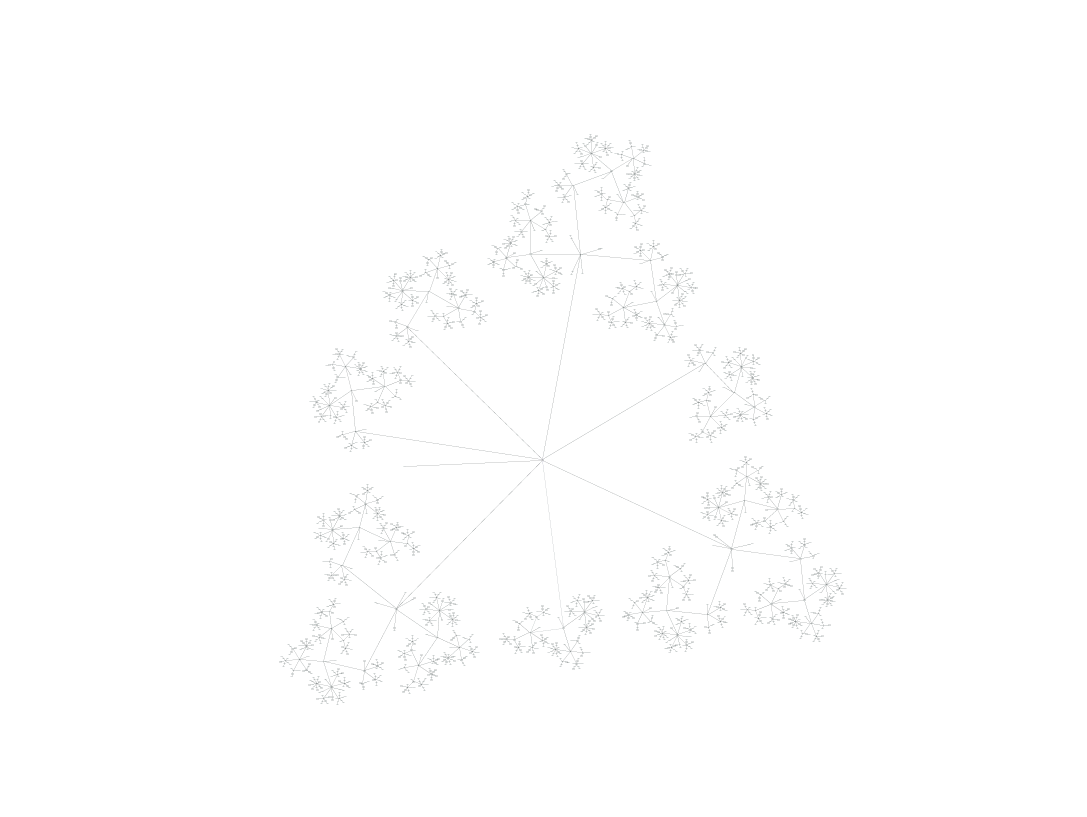
К сожалению, даже в относительно простых случаях довольно быстро происходит взрыв сложности. В данном случае в нашем графе получается 2 670 узлов, которые нужно исследовать, и это занимает намного больше времени, чем в случае с лягушкой — возможно, одну-две секунды.
Во многом это связано с комбинаторной сложностью — например, неважно, какую из двоек мы используем для снятия шока изначально, алгоритм рассматривает это как два отдельных решения, и создаёт для каждого полное дерево ветвящихся решений. В результате мы получаем ветвь, дублирование которой совершенно не нужно. Есть также похожие комбинаторные проблемы при выборе кубиков для погашения, для снятия шока с вооружения и порядка их использования.
Но даже если мы найдём и оптимизируем подобные ненужные ветви (что я в определённой степени и делаю), всегда будет существовать точка, в которой сложность всех возможных перестановок решений ведёт к огромным, медленным деревьям решений, оценка которых займёт бесконечное количество времени. Итак, это первая серьёзная проблема такого подхода. Вот ещё одна:

Отмычка. Разделяет кубик на два.
Этот важный тип вооружения (и подобные ему) вызывает у ИИ проблемы, потому что результат его применения является неопределённым. Если я помещу на него шестёрку, то могу получить пять и один, или четыре и два, а может и две тройки. Я этого не узнаю, пока не сделаю, поэтому очень сложно создать план, который будет это учитывать.
К счастью, в Dicey Dungeons используется отличное решение обеих этих проблем!
Современное решение
Метод Монте-Карло для поиска в дереве (Monte Carlo Tree Search, MCTS) — это вероятностный алгоритм принятия решений. Ниже показано немного странноватое видео, которое, тем не менее, очень хорошо объясняет принцип принятия решений на основе метода Монте-Карло:
По сути, вместо того, чтобы добавлять в граф каждый возможный ход, MCTS проверяет последовательности случайных ходов, а затем отслеживает те из них, которые лучше себя проявили. Благодаря формуле под названием Upper Confidence Bound он волшебным образом может определить, какие ветви дерева решений «наиболее перспективны»:

Кстати, эту формулу я взял из очень полезной статьи про поиск по деревьям методом Монте-Карло. Не спрашивайте меня, как она работает!
Удивительно в MCTS то, что для нахождения наилучшего решения нам обычно не нужно выполнять тупой перебор всего, и мы можем применить такую же абстрактную систему симуляции доски/ходов, как и в минимаксе. То есть мы как бы используем оба алгоритма. Именно такую схему я и использовал в Dicey Dungeons. Сначала она пытается выполнить полное разворачивание дерева решений, что обычно не занимает много времени и приводит к наилучшему результату. Но если дерево кажется слишком большим, то мы откатываемся к использованию MCTS.
У MCTS есть два очень крутых свойства, которые идеально подходят для Dicey Dungeons:
Во-первых, метод идеально работает с неопределённостью. Так как он выполняется снова и снова, собирая данные из каждого прогона, я просто позволяю ему симулировать неопределённые ходы, например, применение отмычки, естественным образом, и спустя множество прогонов метод создаёт достаточно правильный диапазон очков, получаемых в результате этого хода.
Во-вторых, он может дать мне частичное решение. По сути, при работе с MCTS можно выполнять сколько угодно симуляций. Теоретически, если его выполнять бесконечно, он сойдётся к точно таким же результатам, как и минимакс. Однако мне важнее то, что я могу использовать MCTS для получения хорошего решения за ограниченное количество времени обдумывания. Чем больше поисков мы выполняем, тем лучше будет найденное «решение», но в случае Dicey Dungeons часто достаточно всего нескольких сотен поисков, которые занимают малую долю секунды.
Интересные близкие темы
Итак, вот как враги в Dicey Dungeons решают, как вас убить! Я хочу добавить эту систему в ближайшую версию v0.15 игры!
Откуда взялись графы, которые я показывал, в том числе и в twitter:
Я создал их, написав экспортер для GraphML — формата файлов графов с открытыми исходниками, который можно считывать множеством разных инструментов. (Я пользовался отличным yEd, который крайне рекомендую.)
Часть решения этой задачи заключалась в том, чтобы позволить ИИ симулировать ходы, что само по себе является интересной головоломкой. В результате я реализовал систему скриптинга действий. Теперь когда противники используют разные типы вооружений. они выполняют вот такие небольшие скрипты:

Эти небольшие скрипты выполняются hscript — парсером и интерпретатором выражений на основе haxe. Эту часть реализовать было сложно, но усилия себя оправдали: она сделала игру сверхудобной для создания модов. Надеюсь, что после выхода игры люди могут использовать эту систему для разработки собственного вооружения, то есть они смогут добавить в игру практически всё, что способны вообразить. Кроме того, так как ИИ достаточно умён, чтобы оценивать любое передаваемое ему действие, враги смогут разбираться, как пользоваться любым модифицированным вооружением, которое создадут игроки!
Автор: PatientZero





