Я прочитал авторитетную книгу о торговых стратегиях и написал своего торгового робота. К моему удивлению, робот не приносит миллионов, даже торгуя виртуально. Причина очевидна: робот, как гоночный автомобиль, нуждается в «тюнинге», в подборе параметров, адаптированных к конкретному рынку, конкретному периоду времени.
Так как параметров настройки у робота достаточно, перебрать все их возможные комбинации в поисках лучшей, слишком затратная по времени задача. В свое время, решая задачу оптимизации, я не нашел обоснованного выбора алгоритма поиска квазиоптимального вектора параметров торгового робота. Потому решил самостоятельно сравнить несколько алгоритмов…
Краткая постановка задачи оптимизации
Имеем торговый алгоритм. Входные данные — история цен часового интервала за 1 год наблюдений. Выходные данные — P — прибыль либо убыток, скалярная величина.
У торгового алгоритма 4 настраиваемых параметра:
- Mf период “быстрой” скользящей средней,
- Ms период “медленной” скользящей средней
- T — TakeProfit, целевой уровень прибыль по каждой отдельной сделке,
- S — StopLoss, целевой уровень убытка по каждой отдельной сделке.
Каждому из параметров мы задаем диапазон и фиксированный шаг изменения, всего по 20 значений для каждого из параметров.
Таким образом, мы можем искать максимум прибыли (P) для одного параметра на одном массиве входных данных:
- варьируя один параметр, например P = f(Ms), произведя до 20 бэктестов,
- варьируя два параметра, например P = f(Ms, T), произведя до 20 * 20 = 400 бэктестов,
- варьируя три параметра, например P = f(Mf, Ms, T), произведя до 20 * 20 * 20 = 8 000 бэктестов,
- варьируя каждый из параметров, P = f(Mf, Ms, T, S) и произведя до 20^4 = 160 000 бэктестов.
Для большинства торговых алгоритмов, однако, требуется на несколько порядков больше времени для проведения одного теста. Что приводит нас к задаче поиска квазиоптимального вектора параметров без необходимости перебора всего множества возможных их сочетаний.
Тем не менее, трейдинг, и, в частности, алго(ритмический)трейдинг — популярное хобби для многих. Одни самостоятельно программируют торговых роботов, другие идут еще дальше и создают собственные платформы для написания, отладки и бэктестинга торговых стратегий, третьи скачивают / покупают готового электронного “эксперта”. Но даже те, кто не пишут торговые алгоритмы самостоятельно, должны иметь представление о том, как обращаться с этим “черным ящиком”, чтобы извлечь из него прибыль в соответствие с авторской задумкой. Чтобы не быть голословным, дальнейшие свои наблюдения я привожу на примере простой торговой стратегии:
Простой торговый робот
Торговый робот анализирует динамику стоимости золота, в долларах за тройскую унцию, и принимает решение о “покупке” или “продаже” некоторого количества золота. Для простоты примем, что робот всегда торгует одной тройской унцией.
К примеру, на момент покупки, стоимость тройской унции золота составляла 1075.00 USD. На момент последующей продажи (закрытии сделки) цена выросла до 1079.00 USD. Прибыль по этой сделке составила 4 USD.
Если же робот “продал” золото по 1075.00 USD, а впоследствии завершил (закрыл) сделку, “выкупив” золото обратно по цене 1079 USD, прибыль по сделке будет отрицательной величиной — минус 4 USD. Собственно, для нас не имеет значения, каким образом робот продает золото, которым не располагает, чтобы потом “выкупить” его обратно. Брокер / дилинговый центр позволяет трейдеру “покупать” и “продавать” актив тем или иным способом, зарабатывая (или, что чаще, теряя), на разнице курсов.
С входными данными для робота мы определились — это, собственно, временной ряд цен (котировок) золота. Если вы скажете, что мой пример слишком простой, не жизненный — могу вас уверить: большая часть роботов, обращающихся на рынке (да и собственно трейдеров тоже) в своей торговле руководствуются одной лишь статистикой цен на товар, которым торгуют. В любом случае, в задаче параметрической оптимизации торговой стратегии, нет принципиального различия между роботом, торгующего на основании вектора цен и роботом, обращающемуся к терабайтному массиву разносортной рыночной аналитики. Главное, что оба этих робота могут (должны уметь) быть протестированы на исторических данных. Алгоритмы должны быть детерминированы: то есть, на одних и тех же входных данных (модельное время, при необходимости, мы тоже можем принять за параметр), торговый робот должен показывать один и тот же результат.
Более подробно о торговом роботе можно почитать в следующем спойлере:
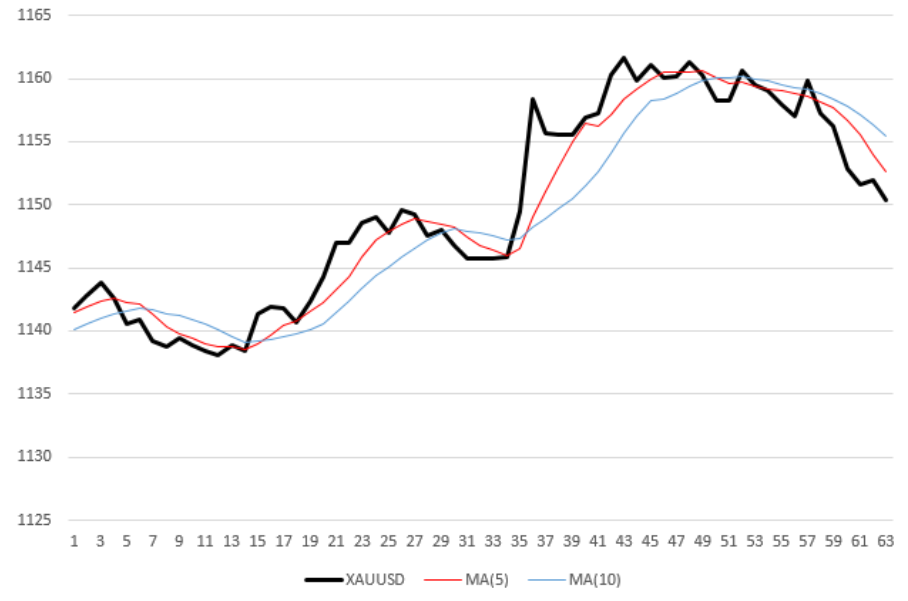
Черная (толстая) кривая на графике — часовые измерения цены XAUUSD. Две тонкие ломаные линии, красная и синяя — усредненные значения цены с периодами усреднения 5 и 10 соответственно. Иначе говоря, скользящие средние (Moving Average, MA) с периодами 5, 10. Например, для того, чтобы рассчитать ординату последней (правой) точки красной кривой, я взял среднее из последних 5 значений цены. Таким образом, каждая скользящая средняя не только “сглажена” относительно ценовой кривой, но и запаздывает относительно нее на половину своего периода.
Правило открытия сделки
Роботу определено простое правило принятие решения о покупке / продаже:
— как только скользящая средняя с коротким периодом (“быстрая” MA) пересекает скользящую среднюю с длинным периодом (“медленную” MA) снизу вверх, робот покупает актив (золото).
Как только “быстрая” MA пересекает “медленную” MA сверху вниз, робот продает актив. На рисунке выше робот совершит 5 сделок: 3 продажи в отметках времени 7, 31 и 50 и две покупки (отметки 16 и 36).
Роботу разрешено открывать неограниченное количество сделок. Например, в какой-то момент робот может располагать несколькими незавершенными покупками и продажами одновременно.
Правило закрытия сделки
Робот закрывает сделку, как только:
- прибыль по сделке превышает указанное в процентах пороговое значение — TakeProfit,
- либо убыток по сделке, в процентах, превышает соответствующее значение — StopLoss.
Предположим, StopLoss равен 0.2%.
Сделка — “продажа” золота по цене 1061.50.
Как только цена золота вырастет до значения 1061.50 + 1061.50 * 0.2% / 100% = 1063.12%, убыток по сделке, очевидно, будет равен 0.2% и робот закроет сделку автоматически.
Все решения о открытии / закрытии сделки робот производит в дискретные моменты времени — на конец каждого часа, после публикации очередной котировки XAUUSD.
Да, робот предельно прост. В то же время, он на 100% соответствует предъявляемым к нему требованиям:
- алгоритм детерминирован: каждый раз, имитируя работу робота на одних и тех же ценовых данных, мы будем получать один и тот же результат,
- имеет достаточное количество настраиваемых параметров, а конкретно: период “быстрой” и период “медленной” скользящей средней (натуральные числа), TakeProfit и StopLoss — положительные вещественные числа,
- изменение каждого из 4 параметров, в общем случае, оказывает нелинейное влияние на характеристики торговли робота, в частности, на его доходность,
- доходность робота на истории цен считается элементарным программным кодом, а сам расчет занимает доли секунды для вектора из тысячи котировок,
- наконец, что, правда, к делу не относится, робот, при всей своей простоте, в реальности проявит себя ничуть не хуже (пусть, вероятно, и не лучше), чем “Грааль”, продаваемый автором в интернет за нескромную сумму.
Быстрый поиск квазиоптимального набора входных параметров
На примере нашего простого робота видно, что полный перебор всех возможных векторов параметров настройки робота слишком затратен даже для 4-х варьируемых параметров. Очевидная альтернатива полному перебору — выбор векторов параметров по определенной стратегии. Рассматриваем лишь часть всех возможных комбинаций в поисках лучшей, в которой ЦФ приближается к наивысшему (либо наименьшему, в зависимости от того, какую ЦФ мы выбрали и какого результата мы добиваемся) значению.
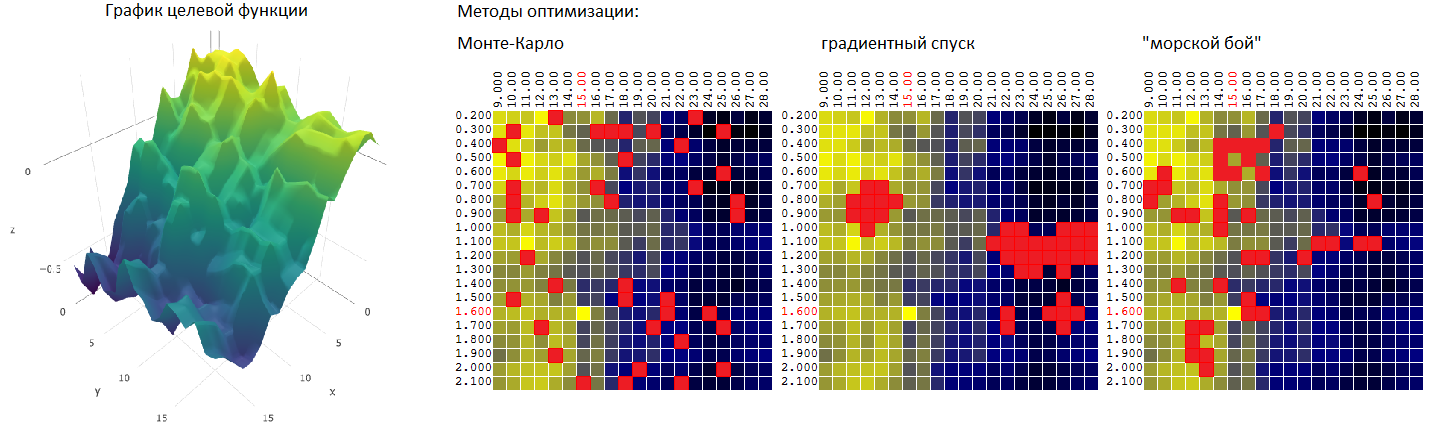
Мы рассмотрим три алгоритма поиска квазиоптимального значения ЦФ. Для каждого алгоритма установим ограничение в 40 тестов (из 400 возможных комбинаций).
Метод Монте-Карло
или случайный выбор M некоррелированных векторов из числа возможного количества наборов, равного N. Метод, вероятно, самый простой из возможных. Будем использовать его как отправную точку для последующего сравнения с остальными методами оптимизации.
Пример 1
график демонстрирует зависимости прибыли (P) нашего торгового робота, торгующего EURUSD, полученной на годовом отрезки истории часовых измерений цены, от значения параметра — период “медленной” скользящей средней (M). Все остальные параметры фиксированы и не подвергаются оптимизации.
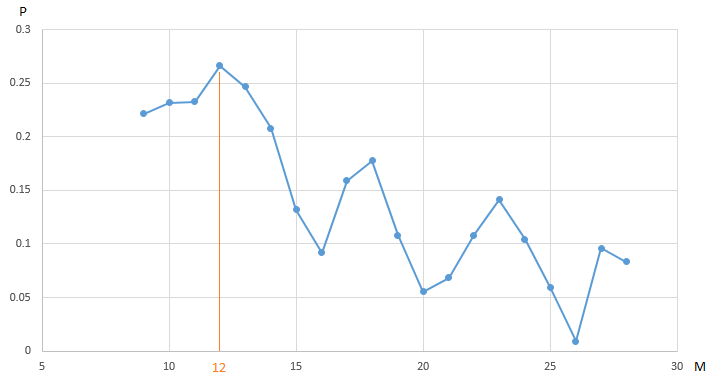
ЦФ (прибыль) достигает максимума 0.27 в точке M = 12. Чтобы гарантированно найти максимальное значение прибыли, нам потребуется провести 20 итераций тестирования. Альтернатива — провести меньшее количество испытаний торгового робота со случайно выбранным значением параметра M на интервале [9, 20]. К примеру, после 5 итераций (20% от общего количества испытаний, мы нашли квазиоптимальный вектор (вектор, очевидно, одномерный) параметров: M = 18 со значением ЦФ (M), равным 0.18:
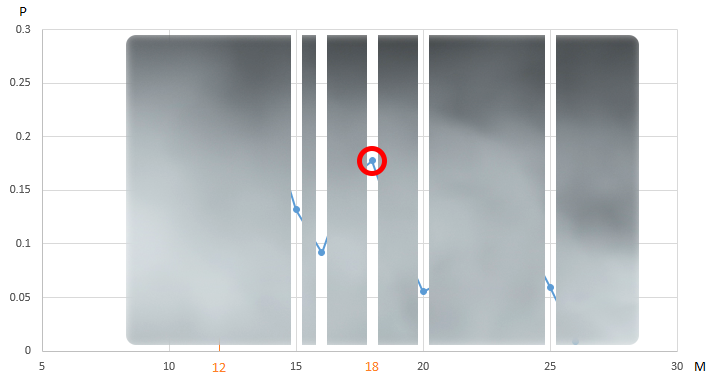
Оставшиеся значения на графике от нашего алгоритма оптимизации скрыл “туман войны”.
Оптимизация одного из четырех параметров нашего торгового робота, при фиксированных значениях остальных параметров, не позволяет нам увидеть всей картины. Возможно, максимум ЦФ, равный 0.27 — не лучшее значение показателя, если варьировать значение других параметров?
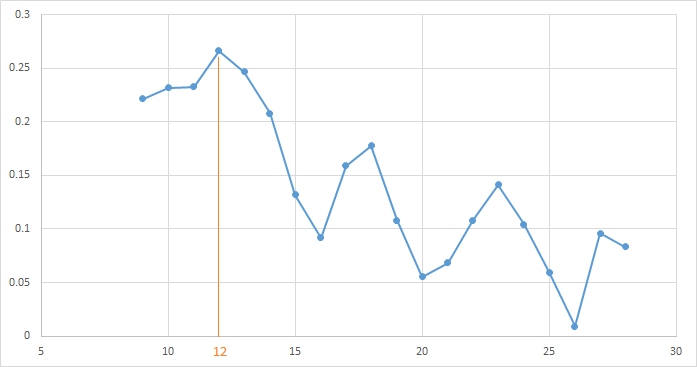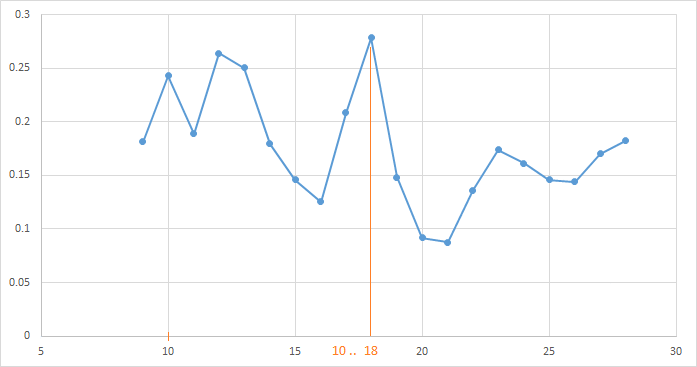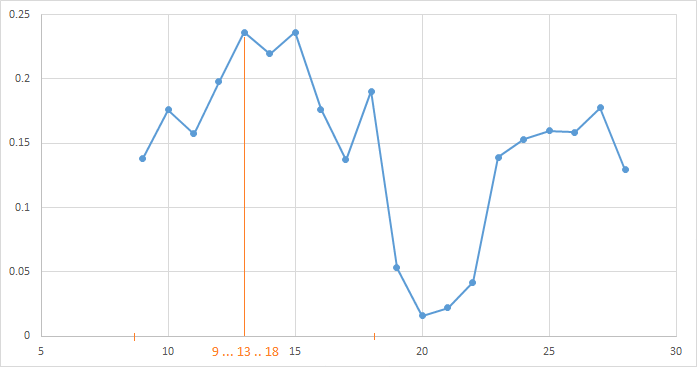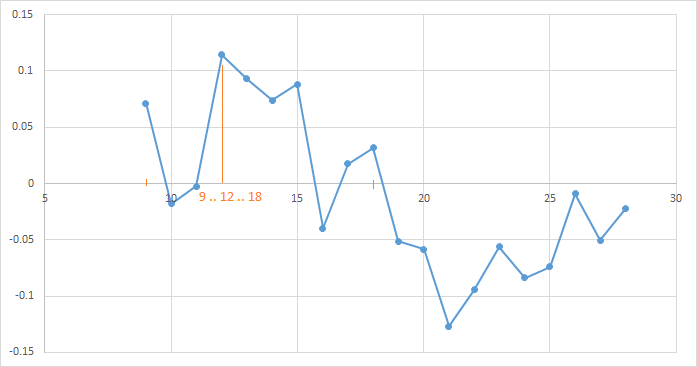
Вот так изменяется зависимость прибыли от периода скользящей средней при различных значениях параметра TakeProfit на интервале [0.2… 0.8].
Метод Монте-Карло: оптимизация двух параметров
Зависимость прибыли торгового робота от двух параметров графически можно изобразить в виде поверхности:
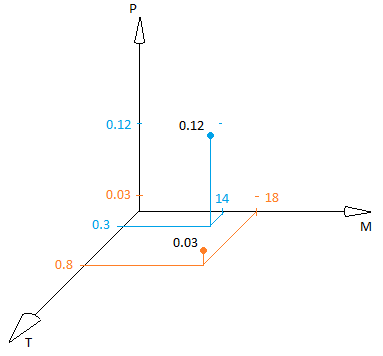
По двум осям отложены значения параметров T (TakeProfit) и M (период скользящей средней), третья ось — значение прибыли.
Для нашего торгового робота, проведя 400 тестов на интервале данных в один год (~6000 часовых котировок евро к доллару США), получим поверхность вида:
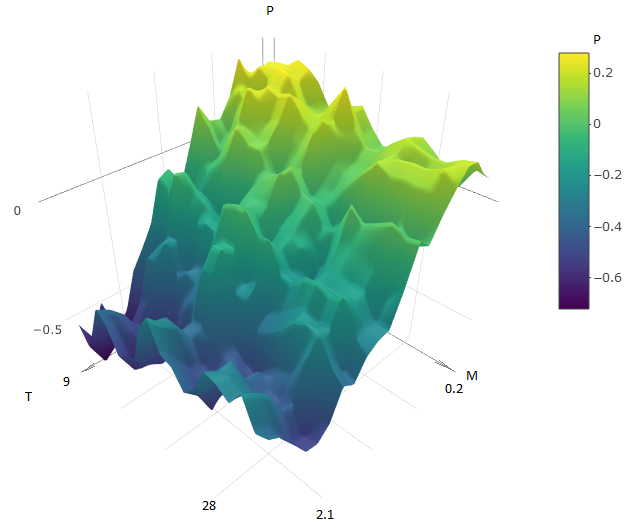
или, на плоскости, где значения ЦФ (прибыль, P) представлены цветом:
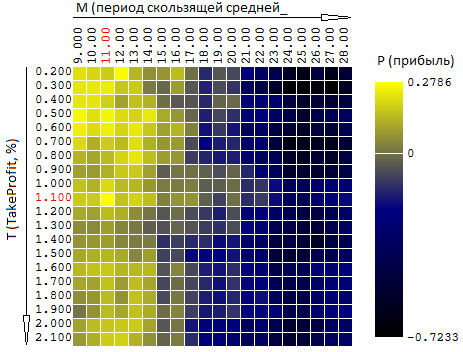
Выбирая произвольные точки на плоскости, в данном примере алгоритм не нашел оптимального значения, но подобрался довольно близко к нему:
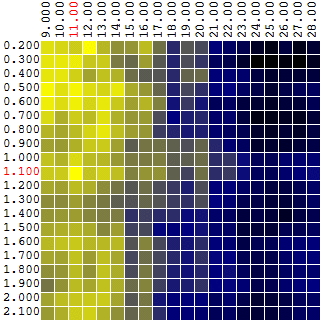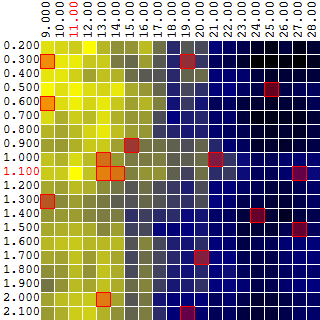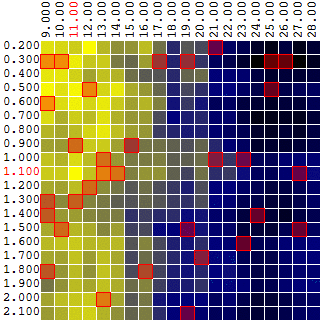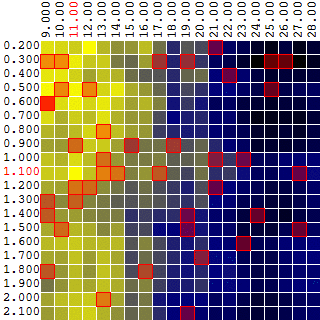
Насколько эффективен метод Монте-Карло в поиске максимума ЦФ? Проведя 1 000 итераций поиска максимума ЦФ на исходных данных из примера выше, я получил следующую статистику:
- среднее значение максимума ЦФ, найденное в ходе 1 000 итераций оптимизации (40 случайных векторов параметров [M, T] из 400 возможных комбинаций), составило 0.231 или 95.7% от глобального максимума ЦФ (0.279).
Очевидно, в сравнении методов параметрической оптимизации торговых роботов одна выборка — не показатель. Но пока достаточно и этой оценки. Переходим к следующему методу — метод градиентного спуска.
Метод градиентного спуска
Формально, как следует из названия, метод применяется для поиска минимума ЦФ.
Согласно методу, мы выбираем стартовый точку с координатами [x0, y0, z0, …]. На примере оптимизации одного параметра это может быть случайно выбранная точка:
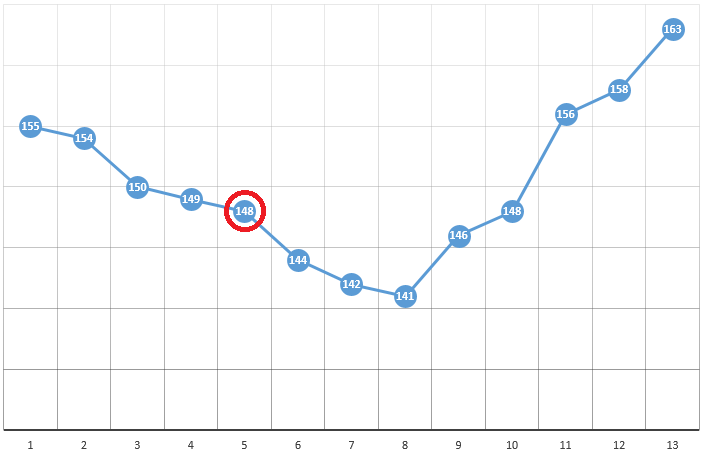
с координатами [5] и значением ЦФ, равным 148. Далее следуют три простых шага:
- проверить значения ЦФ в окрестностях текущей позиции (149 и 144)
- переместиться в точку с наименьшим значением ЦФ
- если такая отсутствует, локальный экстремум найден, алгоритм завершен
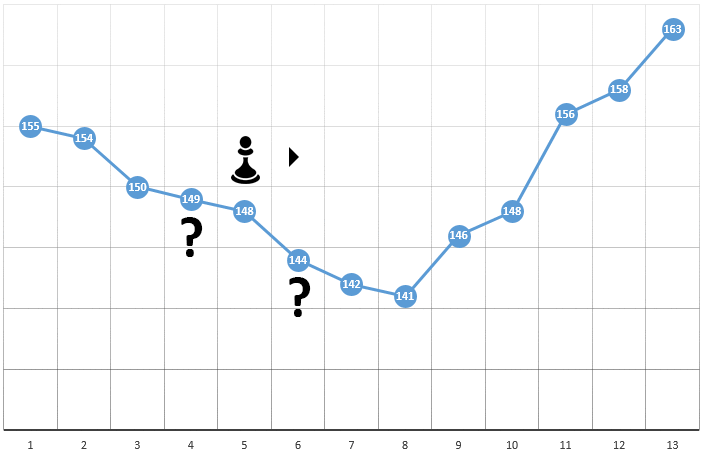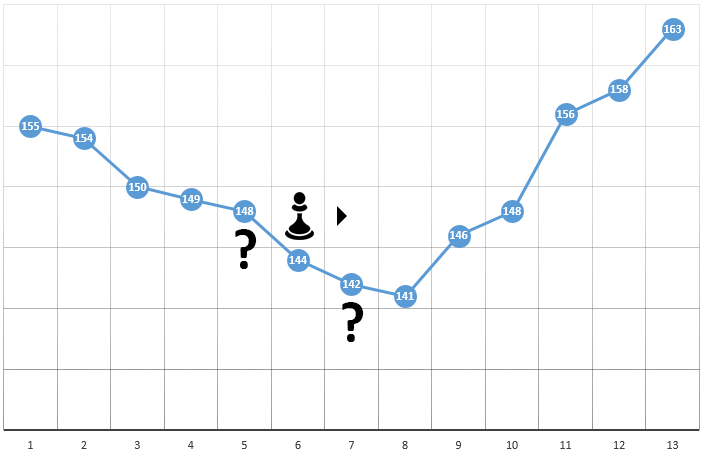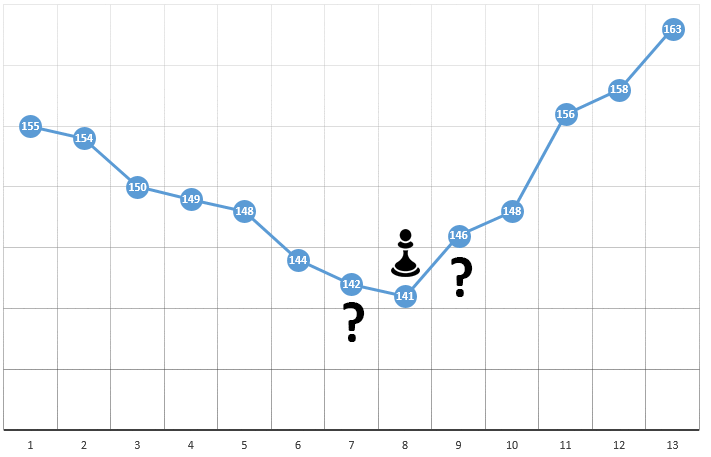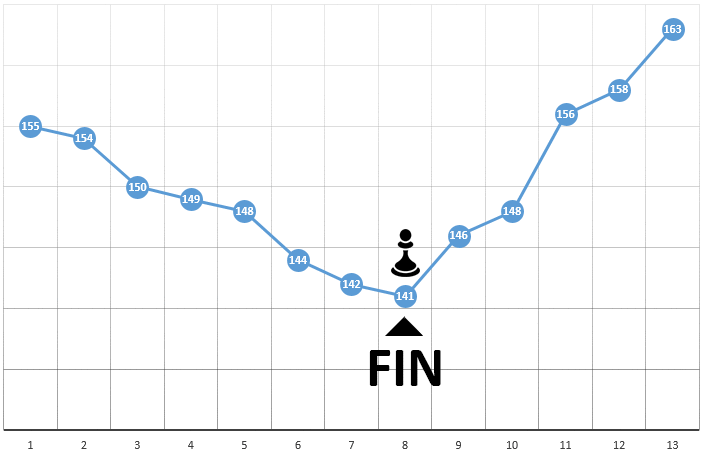
Для оптимизации ЦФ как функции от двух параметров применяем все тот же алгоритм. Если раньше мы вычисляли ЦФ в двух соседних точках ![$[x_{i-1}], [x_{i+1}]$](https://www.pvsm.ru/images/2018/11/16/algoritmy-optimizacii-torgovogo-robota-effektivnyi-sposob-natorgovat-million-zadnim-chislom-12.svg "Алгоритмы оптимизации торгового робота: эффективный способ наторговать миллион задним числом - 12")
, теперь мы проверяем 4 точки:
![$[x_{i-1}, y_i], [x_{i+1},y_i], [x_i, y_{i-1}], [x_i, y_{i+1}].$](https://www.pvsm.ru/images/2018/11/16/algoritmy-optimizacii-torgovogo-robota-effektivnyi-sposob-natorgovat-million-zadnim-chislom-13.svg "Алгоритмы оптимизации торгового робота: эффективный способ наторговать миллион задним числом - 13")
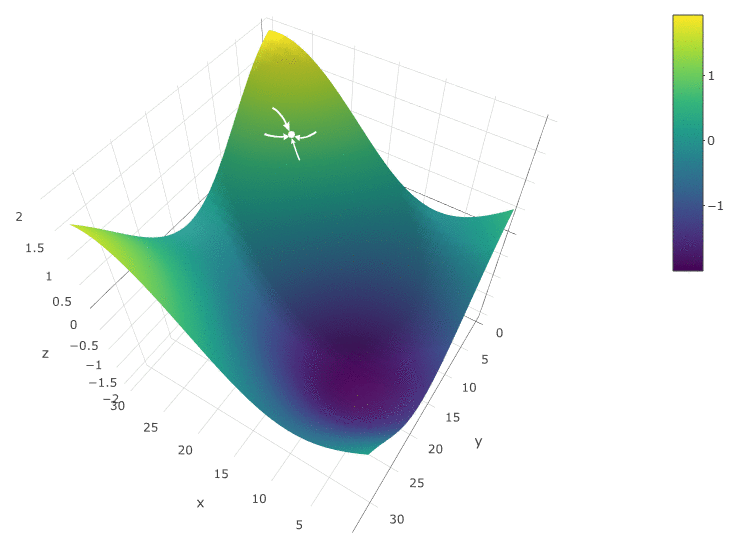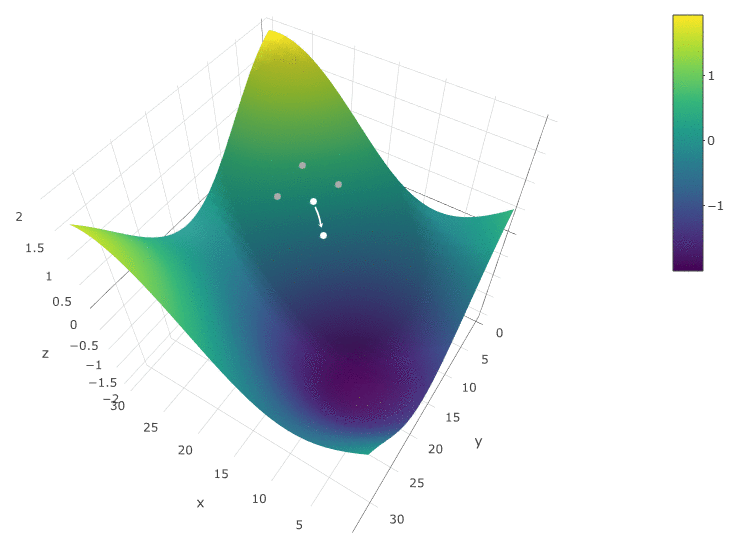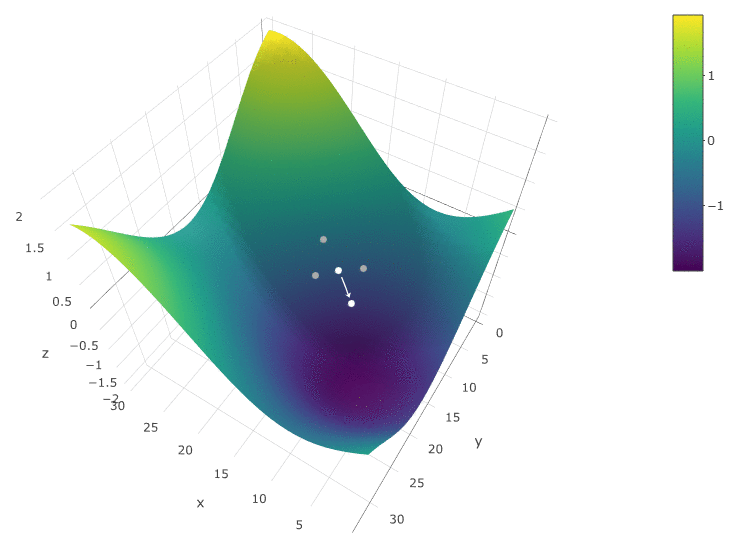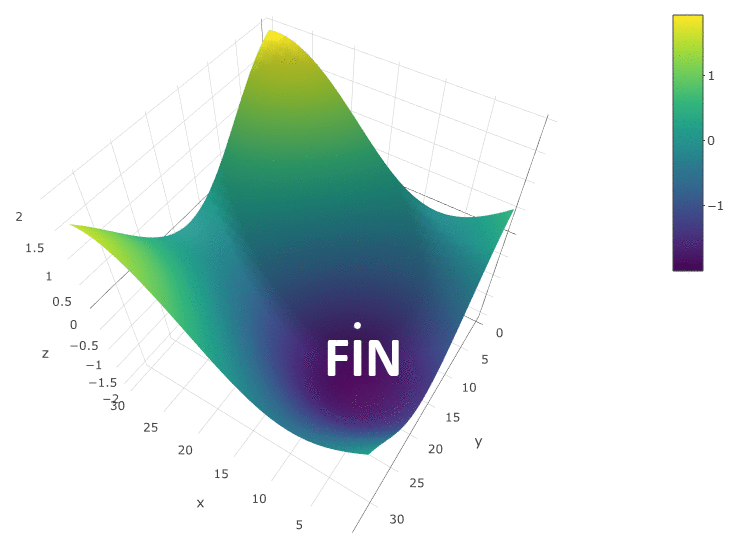
Метод, определенно, хорош, когда у ЦФ на тестируем пространстве всего один экстремум. Если экстремумов несколько, поиск придется неоднократно повторять, чтобы повысить вероятность нахождения глобального экстремума:
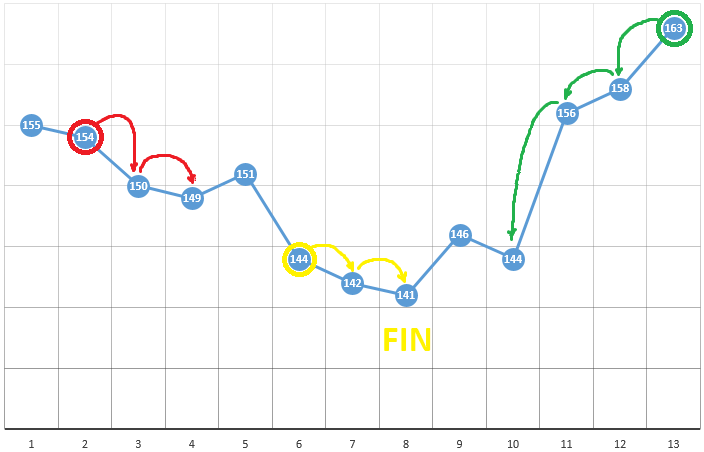
В нашем примере мы ищем максимум ЦФ. Чтобы оставаться в рамках определения алгоритма, мы можем считать, что осуществляем поиск минимума “минус ЦФ”. Все тот же пример, прибыль торгового робота как функция от периода скользящей средней и значения TakeProfit, одна итерация:
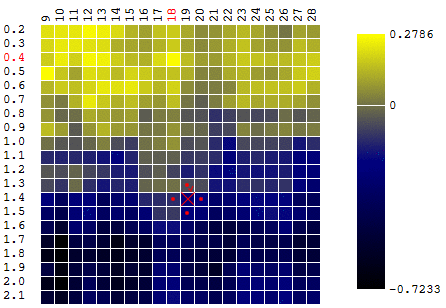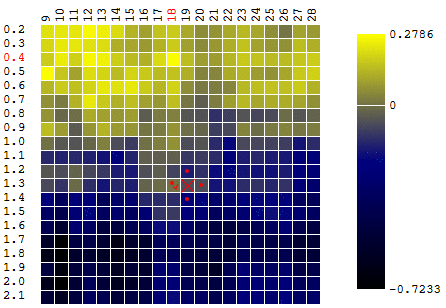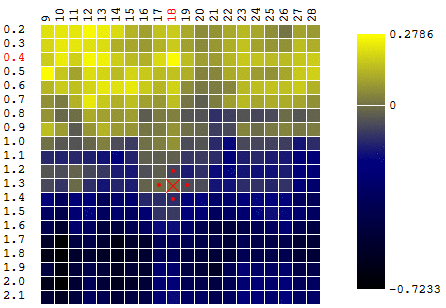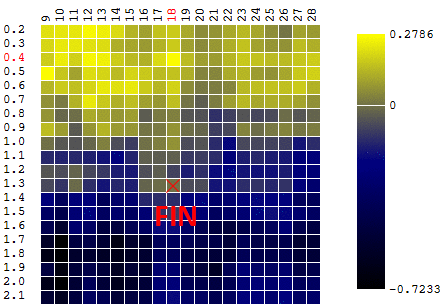
В данном случае был найден локальный экстремум, далекий от глобального максимума ЦФ. Пример нескольких итераций поиска экстремума ЦФ методом градиентного спуска, значение ЦФ рассчитано 40 раз (40 точек из 400 возможных):
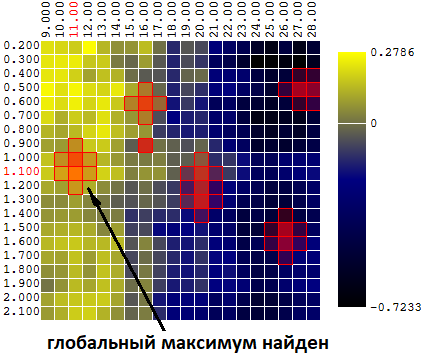
Теперь сравним эффективность поиска глобального максимума ЦФ (прибыли) на наших исходных данных алгоритмами Монте-Карло и градиентного спуска. В каждом случае проводится 40 испытаний (расчетов ЦФ). Произведено по 1 000 итераций оптимизации каждым из методов:
| Монте-Карло | градиентный спуск | |
|---|---|---|
| среднее из полученных квазиоптимальное значение ЦФ | 0.231 | 0.200 |
| полученное значение от максимума ЦФ | 95.7% | 92.1% |
Как видим из таблице, в данном примере метод градиентного спуска хуже справляется со своей задачей — поиска глобального экстремума ЦФ — максимума прибыли. Но не спешим сбрасывать его со счетов.
Параметрическая устойчивость торгового алгоритма
Отыскание координат глобального максимума / минимума ЦФ зачастую не является целью оптимизации. Предположим, на графике встретилась “острая” вершина — глобальный максимум, значение ЦФ в окрестностях которого значительно ниже пикового значения:
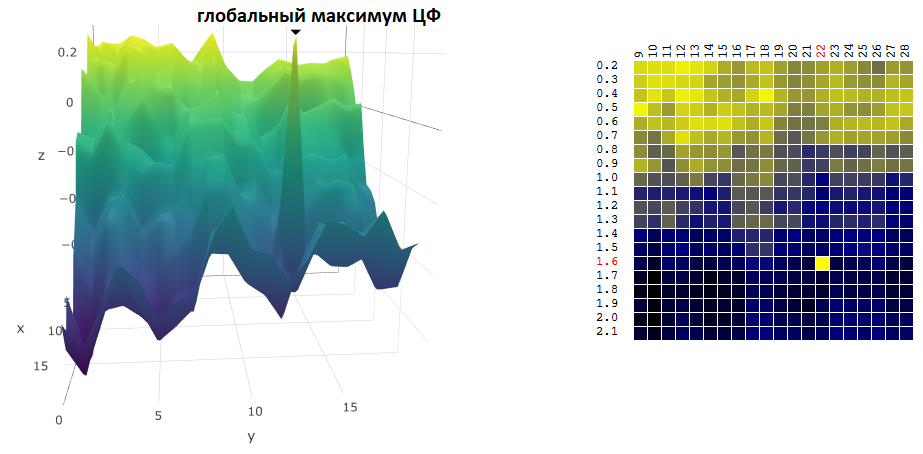
Допустим, мы выбрали настройки торгового робота, соответствующие найденному максимуму ЦФ. Стоит нам незначительно изменить значение хотя бы одного из параметров — период скользящей средней и / или TakeProfit — доходность робота резко упадет (станет отрицательной). Применительно к реальной торговле, можно, как минимум, ожидать, что рынок, на котором предстоит торговать нашему роботу, будет заметно отличаться от того периода истории, на котором мы оптимизировали торговый алгоритм.
Следовательно, при выборе “оптимальных” настроек торгового робота, стоит получить представление о том, насколько робот чувствителен к изменениям настроек в окрестностях найденной точки экстремума ЦФ.
Очевидно, метод градиентного спуска, как правило, дает нам значения ЦФ в окрестностях экстремума. Метод Монте-Карло, скорее, бьет по площадям.
В множественных наставлениях к тестированию автоматических торговых стратегий рекомендуют после завершения оптимизации проверить целевые показатели робота в окрестностях найденного вектора параметров. Но это дополнительные тесты. Вдобавок, что если доходность стратегии упадет при незначительном изменении настроек? Очевидно, придется повторять процесс тестирования.
Нам был бы полезен алгоритм, который, одновременно с поиском экстремума ЦФ позволял бы оценить устойчивость торговой стратегии к изменению настроек в узком диапазоне относительно найденных пиков. Например, искать не непосредственно максимум ЦФ
а средневзвешенное значение, учитывающее соседние значения целевой функции, где вес обратно пропорционален расстоянию до соседнего значения (для оптимизации двух параметров x, y и целевой функции P):
Иначе говоря, при выборе квазиоптимального вектора параметров, алгоритм будет оценивать “сглаженную” целевую функцию:
было
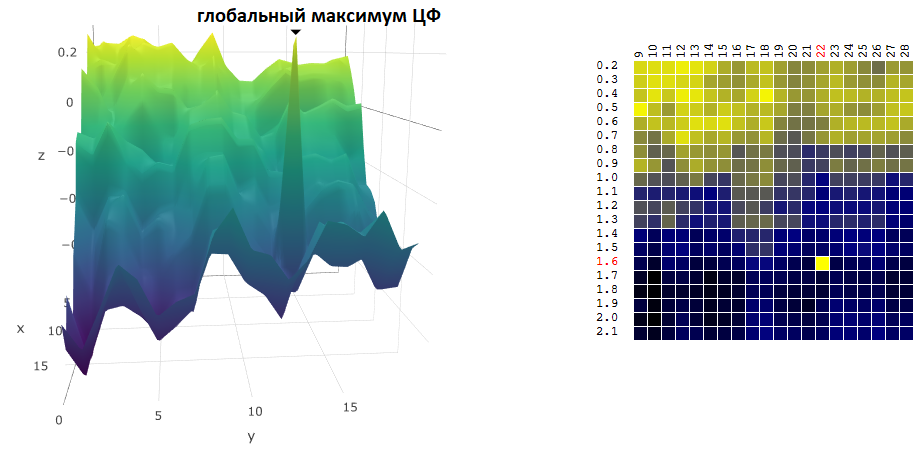
стало
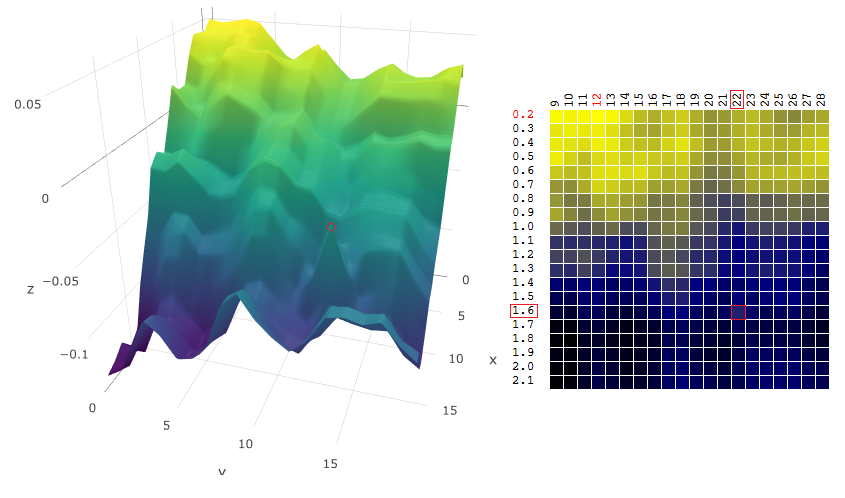
Метод “морской бой”
Пытаясь совместить достоинства обоих методов (Монте-Карло и метод градиентного спуска) я попробовал алгоритм, схожий с алгоритмом игры в “морской бой”:
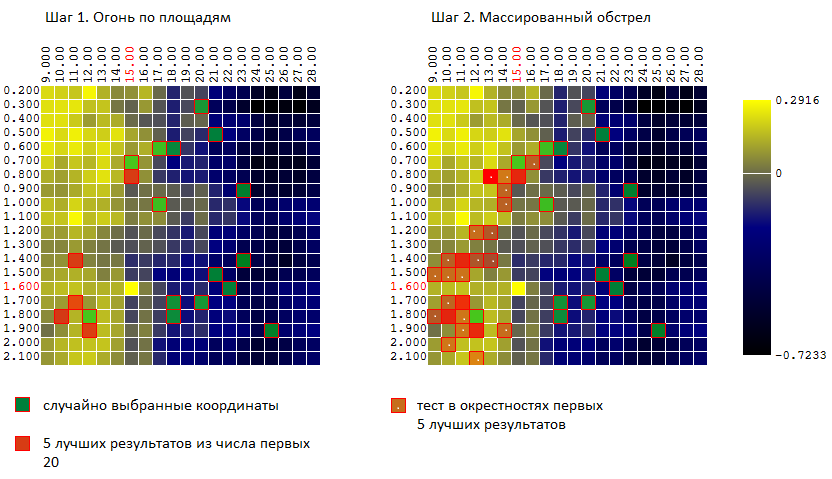
- сначала я наношу несколько “ударов” по всей площади
- затем, в местах “попаданий” открываю массированный огонь.
Иначе говоря, первые N тестов проводятся на случайных некоррелированных векторах входных параметров. Из них отбираются M лучших результатов. В окрестностях этих испытаний (плюс — минут 0..L к каждой из координат) проводится еще K испытаний.
Для нашего примера (400 точек, 40 испытаний всего) имеем:
И снова сравним эффективность теперь уже 3-х алгоритмов оптимизации:
| Монте-Карло | градиентный спуск | “морской бой” | |
|---|---|---|---|
| Среднее значение найденного экстремума ЦФ в процентах от глобального значения. 40 тестов, 1 000 итераций оптимизации |
95.7% | 92.1% | 97.0% |
Результат обнадеживает. Конечно, сравнение проводились на одной конкретной выборке данных: один торговый алгоритм на одном временном ряду стоимости евро по отношению к доллару США. Но, прежде чем сравнить алгоритмы на большем количестве выборок исходных данных, я собираюсь рассказать о еще одном, неожиданно (неоправданно?) популярном алгоритме оптимизации торговых стратегий — генетическом алгоритме (ГА) оптимизации. Однако статья вышла слишком объемной, и ГА придется отложить на следующую публикацию.
Автор: AndreySitaev
