Куча различных способов считывания битов

Возобновляя старую традицию своего блога, я возьму простую задачу, рассмотрю чрезмерно длинный список её альтернативных решений и оценю их достоинства.

Наша простая задача будет заключаться в следующем: мы хотим считать из битового потока данные, закодированные каким-нибудь кодом с переменной длиной бита. Считывание отдельных байтов, машинных слов и т.д. непосредственно поддерживается большинством процессоров и многими языками программирования, но при вводе-выводе с переменной битовой длиной обычно необходимо реализовывать решение самостоятельно.

Это звучит достаточно просто, и в каком-то смысле так и есть. Первый источник проблем заключается в том, что эта операция будет активно использовать кодеки — и да, она будет ограничена вычислениями, а не памятью и вводом-выводом. Поэтому нам нужна не просто рабочая, но и эффективная реализация. И по дороге мы столкнёмся со множеством других сложностей: взаимодействия с буферизацией ввода-вывода, обработка конца буфера, тупиковые ситуации в битовых сдвигах, определённых в C/C++ и в разных архитектурах процессоров, а также другие особенности битовых сдвигов.

В этом посте в основном сосредоточусь на множестве различных способов реализации считывателя; по сути, все рассмотренные здесь техники аналогично применимы и к записывающей части, но я не хочу удваивать количество вариаций алгоритмов. Их и так будет достаточно.

Степени свободы

«Считать переменное количество битов» — это недостаточное описание задачи. Существует множество приемлемых способов упаковки битов в байты, и у всех них есть свои сильные и слабые места, о которых я расскажу позже. Пока же давайте просто остановимся на их различиях.

Для начала нам нужно сделать первый важный выбор — поля будут упаковываться в виде «первым идёт MSB» или «первым идёт LSB» («most significant bit» — наиболее значимый бит и «least significant bit» — наименее значимый бит). То есть если мы вызовем реализуемую функцию getbits и выполним следующий код

a = getbits(4);
b = getbits(3);

для только что открытого битового потока, то мы ожидаем, что оба значения будут получены от одного и того же байта, но как они упорядочены в этом байте? Если упакованы в виде MSB-first, то «a» занимает 4 бита, начиная с MSB, а «b» находится ниже «a», что приводит нас к следующей схеме:

Я нумерую биты так: LSB — это 0 и приближаясь к MSB, значения увеличиваются. Во многих контекстах такой порядок является стандартным. LSB-first представляет собой противоположную ситуацию: первое поле занимает бит 0, а следующие поля содержат увеличивающиеся номера битов:

Оба формата используются в часто встречающихся форматах файлов. Например, в JPEG применяется упаковка битов в битовом потоке в формате MSB-first, а в DEFLATE (zip) используется LSB-first.

Следующий вопрос, который нам нужно решить, заключается в том, что произойдёт, когда значение оказывается растянутым на несколько байтов. Допустим, у нас есть ещё одно значение «c», которое мы хотим закодировать в 5 битах. Что у нас в результате получится? Мы можем слегка отсрочить решение проблемы, объявив, что упаковываем значения в 32-битные или 64-битные слова, а не в байты, но в конце концов нам придётся что-то выбирать. И здесь мы внезапно сталкиваемся со множеством различных вариантов, поэтому я рассмотрю только основных претендентов.

Мы можем воспринимать упаковку битов MSB-first как итерирование по битовому полю «c» от его MSB по направлению к LSB, со вставкой по одному биту за раз. Заполнив один байт, мы приступаем к следующему. Если следовать этим правилам для нашего битового поля c, то в результате в нашем потоке биты окажутся в следующей схеме:

Учтите, что следуя этим правилам, мы в результате придём к тем же двум байтам, которые получили бы, упаковав биты MSB в большой integer и сохранив его в порядке big-endian. Если бы мы вместо этого решили разбить «c» таким образом, чтобы его LSB был в первом байте, а четыре его бита более высшего порядка — во втором байте, то это бы не сработало. Я буду называть такие непротиворечивые правила упаковки битов «естественными» правилами.

Разумеется, у упаковки битов LSB-first существует собственное естественное правило. Оно заключается во вставке нового значения бит за битом, начиная с LSB и вверх, и если мы так сделаем, то в результате получим следующий битовый поток:

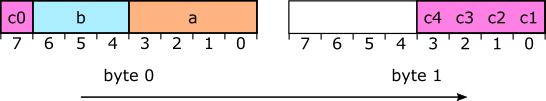
Естественная упаковка LSB-first даёт нам те же байты, что и упаковка LSB-first в большой integer с сохранением его в порядке байтов little-endian. Кроме того, у нас на рисунке возникает очевидная неуклюжесть: логически сопряжённая упаковка поля «c» в несколько байтов выглядит на таком рисунке прерывистой, в то время как рисунок упаковки MSB-first выглядит так, как мы того и ожидаем. Но и в нём возникает проблема: в рисунке MSB-first мы нумеруем биты в увеличивающемся справа налево порядке (стандартном), а байты — в увеличивающемся слева направо порядке (что тоже является стандартным).

Вот, что происходи со схемой битов LSB-first, если мы нарисуем бит 0 (LSB) в каждом байте слева, а бит 7 (MSB) — справа:

Если нарисовать так, то схема будет выглядеть ожидаемым нами способом. Расположение MSB справа кажется странным, если думать о байте как о числе, но гораздо менее странным оказывается, если думать о нём как о массиве из 8 бит (как мы, по сути, и работаем с ним при выполнении побитового ввода-вывода).

По совпадению, в некоторых big-endian-архитектурах (например, в IBM POWER) биты нумеруются следующим образом — бит 0 — это MSB, бит 31 (или 63) — LSB. Создав схему упаковки битов MSB-first на такой машине с битом 0=MSB, и нумеруя наши собственные битовые поля таким образом, чтобы их бит 0 соответствовал MSB, мы получим точно такую же схему (но это будет означать, что что-то немного отличается). Этот стандарт делает порядок битов и байтов согласующимся (что хорошо), но разрушает удобный стандарт соответствия бита k значению 2^k (что не совсем хорошо).

И если мысль о перенумерации битов таким образом, чтобы бит 0 являлся MSB, взрывает вам мозг, то можно оставить нумерацию битов неизменной, но стать бунтарём и рисовать адреса байтов увеличивающимся слева. Или же увеличивать адреса вправо, но стать немного другим бунтарём и записывать байтовый поток в обратном порядке. Если выбрать один из этих вариантов, то мы получим следующую схему:

Я понимаю, что это уже начинает запутывать, и на этом остановлюсь, но здесь нужно сказать о важном: не стоит слишком привязываться к способу получения байтов. Легко обмануться, решив, что один вариант лучше другого просто потому, что он выглядит лучше, но стандарты получения байтов слева направо и битов внутри них справа налево совершенно произвольны, поэтому какой бы вы ни выбрали, у вас в результате всё равно получится что-то странное.

Получается у каждого из стандартов упаковки MSB-first и LSB-first есть свои достоинства и недостатки, и гораздо полезнее будет думать о них как об инструментах с разными областями применения, а не назначать один из них «правильным», а другие «ошибочными». Что касается порядка байтов и необходимости упаковки значений в байты, слова или что-то более крупное, то я крайне рекомендую вам использовать наиболее естественный порядок для вашего стандарта упаковки битов: MSB-first естественным образом соответствует порядку байтов в стиле big-endian, а LSB-first естественно соответствует порядку байтов little-endian. Если только вы не записываете байтовые потоки в обратном порядке (верите или нет, но есть логичные причины поступать и так); в этом случае у нас получается MSB-first в обратном порядке, соответствующий little-endian, и LSB-first в обратном порядке, соответствующий big-endian.

Причина выбора «естественных» порядков заключается в том, что они дают нам в разных реализациях бОльшую свободу. Поток с естественным порядком позволяет использовать множество различных декодеров (и кодеров), у каждого из которых есть свои компромиссы (и свои преимущества в разных случаях). «Неестественные» порядки обычно применяются с одной конкретной реализацией и при декодировании любым другим способом оказываются очень неудобными.

Наш первый getbits (извлечение битов)

Теперь, когда мы в достаточном объёме описали задачу, можем реализовать решение. Особо простая версия возможна, если предположить, что весь битовый поток расположен в памяти последовательно (как массив байтов), и пока полностью игнорировать неприятные проблемы наподобие попадания в конец массива. Давайте просто притворимся, что он бесконечен! (Или достаточно огромен, или имеет по краям заполнение нулями.)

В этом случае мы можем основать реализацию на чисто функциональной функции «извлечения битов», в которой я проиллюстрирую возникающие проблемы и всевозможные функции считывания битов. Давайте начнём с упаковки битов LSB-first:

// Считаем buf[] одним гигантским числом integer little-endian, получаем "width"
// битов, начиная с номера бита "pos" (LSB=бит 0).
uint64_t bit_extract_lsb(const uint8_t *buf, size_t pos, int width) {
    assert(width >= 0 && width <= 64 - 7);

    // Считываем 64-битное число little-endian, начиная с байта,
    // содержащего бит номер "pos" (относительно "buf").
    uint64_t bits = read64LE(&buf[pos / 8]);

    // Смещаем биты внутри первого байта, который
    // мы уже считали.
    // После этого LSB нашего битового поля является LSB битов.
    bits >>= pos % 8;

    // Возвращаем нижние "width" битов, обнуляя остальные с помощью битовой маски.
    return bits & ((1ull << width) - 1);
}

// Переменная состояния, предполагается локальной или
// принадлежащей какому-нибудь объекту.
const uint8_t *bitstream; // Входящий битовый поток
size_t bit_pos; // Текущая позиция в потоке в битах.

uint64_t getbits_extract_lsb(int width) {
    // Считывание битов
    uint64_t result = bit_extract_lsb(bitstream, bit_pos, width);
    // Перемещаем курсор
    bit_pos += width;
    return result;
}

Мы просто воспользовались тем упомянутым выше фактом, что битовый поток LSB-first — это просто большое число little-endian. Сначала мы получаем 64 смежных, упорядоченных в байты битов, начиная с первого байта, содержащего любые из интересующих нас битов, совершаем сдвиг вправо, чтобы избавиться от оставшихся лишних 0-7 битов ниже первого нужного нам бита, а затем возвращаем результат, маской приведённый к нужной ширине.

В зависимости от значения pos, это смещение вправо может стоить нам дополнительных 7 битов. Поэтому хотя мы и считываем полные 64 бита, максимальное количество, которое мы можем считать за один раз с помощью этого кода, равно 64-7=57 битам.

Имея bitextract, мы запросто можем реализовать getbits; мы просто отслеживаем текущую позицию битового потока (в битах), и выполняем его инкремент после считывания.

Соответствующий вариант для MSB-first получается довольно похожим образом, за исключением одной раздражающей проблемы, о которой я расскажу после демонстрации кода:

// Считаем buf[] одним гигантским числом integer big-endian, получаем "width"
// битов, начиная с номера бита "pos" (MSB=бит 0).
uint64_t bit_extract_msb(const uint8_t *buf, size_t pos, int width) {
    assert(width >= 1 && width <= 64 - 7);

    // Считываем 64-битное число big-endian, начиная с байта,
    // содержащего бит номер "pos" (относительно "buf").
    uint64_t bits = read64BE(&buf[pos / 8]);

    // Смещаем биты внутри первого байта, который мы уже считали.
    // После этого MSB нашего битового поля находится в MSB битов.
    bits <<= pos % 8;

    // Возвращаем верхние "width" битов.
    return bits >> (64 - width);
}

uint64_t getbits_extract_msb(int width) {
    // Считываем биты
    uint64_t result = bit_extract_msb(bitstream, bit_pos, width);
    // Перемещаем курсор
    bit_pos += width;
    return result;
}

Этот код работает аналогично предыдущему: считываем 64 смежных, упорядоченных в байты бита (на этот раз big-endian), выполняем сдвиг влево, чтобы выровнять верх нужного нам битового поля с MSB bits (в то время как раньше мы делали сдвиг вправо, чтобы выровнять низ нашего битового поля с LSB bits), а затем делаем сдвиг вправо, чтобы расположить верхние width битов внизу для их возврата, потому что при вызове getbits(3) мы обычно ожидаем увидеть значение от 0 до 7.

Граничные случаи сдвигов

Так в чём же проблема? Эта версия кода не позволяет width быть равной нулю. Проблема в том, что если мы позволим сделать width == 0, то конечный сдвиг попытается сдвинуть вправо 64-битное значение на 64 бита, а в C/C++ это неопределённое поведение! В таком случае мы можем выполнять сдвиг на 0-63 байта.

В некоторых случаях C/C++ оставляет детали неопределёнными для обратной совместимости с машинами, поэтому никто сейчас об этом не беспокоится. Известный пример: отсутствие требования того, чтобы представление знаковых чисел использовало дополнительный код; хотя архитектуры без дополнительного кода существуют, все они сегодня сохранились лишь в музеях.

К сожалению, у нас не один из таких случаев. Вот, что происходит на разных широко распространённых архитектурах CPU, когда величина сдвига находится вне пределов интервала:

• Для 32-битных x86 и x86-64 величины сдвига интепретируются как mod 32 для ширины операндов 32 бит и ниже, и mod 64 для 64-битных операндов. То есть сдвиг вправо 64-битного значения на 64 в результате даст то же, что и сдвиг на 0, т.е. отсутствие операции (no-op).
• В 32-битных ARM (наборы инструкций A32/T32) величины сдвига берутся mod 256. Сдвиг вправо 32-битного значения на 32 (или 64) в результате даст 0, как и сдвиг вправо на 255, но сдвиг вправо на 256 оставит значение нетронутым.
• В 64-битных ARM (A64 ISA) величины сдвига берутся mod 32 для 32-битных сдвигов и mod 64 для 64-битных сдвигов (по сути так же, как и в x86-64).
• RISC-V тоже следует тому же правилу: расстояния 32-битных сдвигов берутся как mod 32, расстояния 64-битных сдвигов — как mod 64.
• В POWER/PowerPC 32-битные сдвиги берут величину сдвига mod 64, а 64-битные сдвиги берут величину сдвига mod 128.

Чтобы ещё более запутать нас, большинство этих наборов инструкций имеют расширения SIMD, а целочисленные инструкции SIMD обладают другим поведением при сдвиге вне пределов интервала, отличающимся от инструкций не-SIMD. Если вкратце, то это один из тех случаев, когда присутствуют архитектурные различия между популярными платформами; для большинства из вас POWER и RISC-V могут показаться немного устаревшими, но, допустим, 32-битные и 64-битные ARM установлены на данный момент в сотнях миллионов устройств.

Следовательно, даже если всё, что делает компилятор с этим сдвигом вправо — это отдаёт соответствующую инструкцию сдвига вправо для целевой архитектуры (а обычно так и происходит), то мы будем видеть на разных архитектурах разное поведение. На ARM A64 и x86-64 результат сдвига на 64 по сути будет no-op, а getbits(0) поэтому будет (обычно) возвращать ненулевое значение, хотя следует ожидать, что возвращаться должен ноль.

Почему же это так важно? Разумеется, жёстко прописанный в коде getbits(0) не является интересным случаем применения; однако иногда нам необходимо выполнить getbits(x) для какой-то переменной x, где x в некоторых случаях может быть нулём. В этом случае было бы здорово, чтобы код просто работал и не требовал каких-то проверок особых случаев.

Если вы хотите, чтобы этот случай работал, то одним из вариантов будет явная проверка на width == 0 и обработка этого особым образом; другим вариантом будет использование выражения без ветвления, работающего с нулевыми ширинами, например, этого кода, применяемого в FSE Йенна Коллета:

    // Возвращаем верхние "width" бит, избегая граничных случаев с width==0.
    return (bits >> 1) >> (63 - width);

Этот конкретный случай проще обрабатывать для битовых потоков LSB-first. И поскольку я упомянул их, давайте поговорим об операции использования маски, которую я применил для изолирования нижних width битов:

    // Возвращаем нижние "width" бит, обнуляя остальные с помощью битовой маски.
    return bits & ((1ull << width) - 1);

Существует аналогичная форма, которая немного менее затратна в архитектурах с трёхоперандной инструкцией and-with-complement (AND-NOT). К ним относятся многие процессоры RISC CPU, а также x86s с BMI1. А именно, мы можем взять маску всех битов-единиц, выполнить сдвиг влево, чтобы добавить внизу width нулей, а затем дополнить всё:

    return bits & ~(~0ull << width);

Если у вас x86 не только с BMI1, но и с поддержкой BMI2, вы также можете использовать инструкцию BZHI, специально созданную для такого случая, если разберётесь с тем, как заставить компилятор отдать её (или использовать ассемблер). Ещё один вариант, который в некоторых случаях будет предпочтительным — просто подготовить небольшую таблицу поиска битовых масок, которая упрощает код до такого:

    return bits & width_to_mask_table[width];

Подготовка таблицы поиска, хранящей результат двух целочисленных операций, может показаться смешным действием, особенно потому что вычисление адреса загружаемого элемента таблицы обычно включает в себя и сдвиг, и сложение — ровно те же самые операции, которые мы бы выполняли, если бы у нас не было таблицы! — но в этом безумии есть свой метод: вычисление требуемого адреса может выполняться как часть доступа к памяти в одной инструкции загрузки, например, на машинах с x86 и ARM, поэтому эти сдвиг и сложение вычисляются в блоке генерации адреса (Address Generation Unit, AGU) как часть конвейера загрузки в ЦП, а не с инструкциями целочисленной арифметики и сдвига. То есть подобное контринтуитивное решение заменить две целочисленные инструкции ALU одной инструкцией загрузки целого числа может привести к значительному ускорению кода с активным битовым вводом-выводом, потому что оно лучше уравновешивает нагрузку между разными операционными блоками.

Ещё одно интересное свойство заключается в том, что версия LSB-first, использующая таблицу поиска масок, выполняет один сдвиг на переменную величину (чтобы сдвинуть уже считанные биты). Это важно, потому что по множеству (часто банальных!) причин во многих микроархитектурах сдвиги целых чисел на переменные величины более затратны, чем сдвиги на постоянные величины времени компилирования. Например, Cell PPU/Xbox 360 Xenon были печально известны тем, что имели сдвиги на переменное расстояние, тормозившие ядро процессора на ужасно долгое время — 12 циклов, а обычные сдвиги были встроены в конвейер и выполнялись за два цикла. На многих микроархитектурах Intel x86 «традиционные» переменные сдвиги x86 (SHR reg, cl и подобные им) в три раза затратнее, чем сдвиги на константу времени компилирования.

Кажется, что это ещё одна причина отказа от варианта MSB-first: рассмотренные выше варианты выполняют два или три сдвига на операцию извлечения битов, два из которых имеют переменное расстояние. Но существует трюк, благодаря которому можно вернуться к операции с одиночным сдвигом, а именно использование вместо обычного сдвига циклического:

// Считаем buf[] одним гигантским числом integer big-endian, получаем "width"
// битов, начиная с номера бита "pos" (MSB=бит 0).
uint64_t bit_extract_rot(const uint8_t *buf, size_t pos, int width) {
    assert(width >= 0 && width <= 64 - 7);

    // Считываем 64-битное число big-endian, начиная с байта,
    // содержащего бит номер "pos" (относительно "buf").
    uint64_t bits = read64BE(&buf[pos >> 3]);

    // Выполняем поворот влево, чтобы выровнять низ нашего битового поля с LSB.
    bits = rotate_left64(bits, (pos & 7) + width);

    // Возвращаем нижние "width" бит.
    // (Здесь с использованием таблицы, но также будут работать и другие
    // способы использования масок в битовом вводе-выводе LSB-first.)
    return bits & width_to_mask_table[width];
}

Здесь поворот влево (вы должны сами выяснить, как наилучшим образом использовать его в вашем компиляторе C) сначала выполняет работу исходного сдвига влево, а затем выполняет поворот на дополнительные «width» бит, чтобы заставить битовое поле перевернуться от наиболее значимых битов значения к наименее значимым, после чего к ним можно применить маску так же, как и в варианте LSB-first.

А, да, и я начал писать деление на 8 как сдвиг право на 3, и mod-8 нашей беззнаковой позиции как двоичное AND с 7. Это эквивалентные замены, и вы можете увидеть такие формы в настоящем коде, поэтому я решил их сюда добавить.

С помощью такой операции маски поворотом мы (в RAD Game Tools) выполняли считывание битов в Cell PPU и Xbox 360, только потому, что на этом ядре сдвиги с переменным расстоянием были так ужасны. Стоит заметить, что у этой версии тоже нет проблем с width == 0; единственная проблема — это зависимость от инструкций поворота, которые существуют (и быстро выполняются) в большинстве архитектур, но обычно к ним неудобно получать доступ из кода на C.

Мы уже обсудили множество различных способов выполнения битового сдвига и маскирования, и в дальнейшем я буду ссылаться на них. Но я ещё не показал вам никакой практической логики битового ввода-вывода: форма извлечения битов — это хорошая стартовая точка, удобная для объяснения концепций, не задумываясь о состоянии, но в реальном коде вы скорее всего не будете использовать её, не в последнюю очередь потому, что она предполагает, что весь битовый поток находится в памяти и его можно легко считать до конца буфера в обычном процессе выполнения!

Итак, мы определились с основной задачей и рассмотрели различные способы выполнения сдвига и использования масок, обнаружив свойственные им сложности. Выбранная мной форма «извлечения битов» основана на примитиве без состояния, с которого удобно было начинать, потому что в нём не использовались инварианты цикла.

Сейчас мы перейдём к стилю с состоянием, который используется в большинстве считывателей битов, которые вы встретите (потому что он оказывается наименее затратным). Также мы перейдём от монолитной функции getbits к чему-то более разбитому на части. Но давайте начнём с начала.

Вариант 1: считывание ввода по одному байту за раз

Наш считыватель-«извлекатель» предполагал, что весь битовый поток заранее находится в памяти. Это не всегда возможно или желательно; давайте исследуем другой предельный случай, а именно считыватель битов, запрашивающий дополнительные биты по одному за раз и только тогда, когда они нужны.

В общем случае наши варианты с состоянием будут получать ввод по несколько байт за раз, и у них будут несколько частично обработанных байтов. Нам нужно хранить эти данные в переменной, которую мы назовём «битовым буфером»:

// Здесь переменные снова считаются состоянием побитового считывателя
// или локальными, а не глобальными переменными.
uint64_t bitbuf = 0;   // значение битов в буфере
int      bitcount = 0; // количество битов в буфере

В процессе обработки ввода мы всегда будем записывать новые биты в этот буфер, когда он заканчивается, или при возможности считывать биты из этого буфера.

Без лишних слов давайте создадим нашу первую реализацию getbits, считывающую по одному байту за раз, и на этот раз начнём с MSB-first:

// Инвариант: в "bitbuf" есть "bitcount" битов, сохранённых с
// MSB сверху вниз; остальные биты в "bitbuf" - это 0.

uint64_t getbits1_msb(int count) {
    assert(count >= 1 && count <= 57);

    // Продолжаем считывать дополнительные байты, пока не буферизируем достаточное количество битов
    // Big endian; наши текущие биты находятся наверху слова,
    // новые биты добавляются снизу.
    while (bitcount < count) {
        bitbuf |= (uint64_t)getbyte() << (56 - bitcount);
        bitcount += 8;
    }

    // Теперь у нас присутствует достаточно битов; наибольшие значимые 
    // "count" биты из "bitbuf" являются нашим результатом.
    uint64_t result = bitbuf >> (64 - count);

    // Теперь удаляем эти биты из буфера
    bitbuf <<= count;
    bitcount -= count;

    return result;
}

Как и раньше, мы можем избавиться от требования count≥1, изменив способ получения битов результата, как объяснено в предыдущей части. Я упоминаю об этом в последний раз; просто учитывайте, что каждый раз, когда я буду показывать какой-нибудь вариант алгоритма, то к нему автоматически применяются предыдущие вариации.

Идея здесь довольно проста: сначала мы проверяем, достаточно ли в буфере битов для немедленного удовлетворения запроса. Если нет, то мы записываем дополнительные байты по одному за раз, пока у нас не будет их достаточно. Здесь подразумевается, что getbyte() в идеале будет использовать некий механизм буферизированного ввода-вывода, который просто сводится к разыменованию и инкременту указателя на критическом пути; если этого можно избежать, он не должен быть вызовом функции или чем-то затратным. Поскольку мы вставляем по 8 бит за раз, то за один вызов мы можем считать максимум 57 бит; это наибольшее количество битов, на которое мы можем пополнить буфер, не рискуя при этом ничего упустить.

После этого мы получаем верхние count битов из буфера, а затем смещаем их. Сохраняемый здесь инвариант заключается в том, что первый несчитанный бит хранится в MSB буфера.

Стоит также заметить, что этот процесс удобно разбивается на три отдельные операции меньшего объёма, которые я назову «пополнение» (refill), «просмотр» (peek) и «потребление» (consume). Фаза «пополнения» гарантирует, что в буфере будет присутствовать минимальное количество бит; «просмотр» возвращает несколько следующих битов в буфере, не отбрасывая их, а «потребление» удаляет биты, не глядя на них. Все они оказываются полезными по отдельности операциями; чтобы показать, как всё это организуется, я покажу эквивалент алгоритма LSB-first, разделённого на меньшие части:

// Инвариант: в "bitbuf" есть "bitcount" битов, сохранённых с
// LSB в снизу вверх; остальные биты в "bitbuf" - это 0.
void refill1_lsb(int count) {
    assert(count >= 0 && count <= 57);
    // Новые байты вставляются в верхний конец.
    while (bitcount < count) {
        bitbuf |= (uint64_t)getbyte() << bitcount;
        bitcount += 8;
    }
}

uint64_t peekbits1_lsb(int count) {
    assert(bit_count >= count);
    return bitbuf & ((1ull << count) - 1);
}

void consume1_lsb(int count) {
    assert(bit_count >= count);
    bitbuf >>= count;
    bitcount -= count;
}

uint64_t getbits1_lsb(int count) {
    refill1_lsb(count);
    uint64_t result = peekbits1_lsb(count);
    consume1_lsb(count);
    return result;
}

Запись getbits в виде сочетания таких трёх меньших примитивов не всегда оптимальна. Например, если мы используем метод поворота для битовых буферов MSB-first, то хотим, чтобы поворот был разделён между фазами peekbits и consume; оптимальная реализация разбивает работу на эти две фазы. Однако разбить код на эти отдельные этапы всё равно полезно, потому что когда вы освоите все эти три фазы как отдельные этапы, то сможете по-разному использовать их вместе.

Смотрим вперёд

Наиболее важная такая транформация — это амортизация пополнения для нескольких операций декодирования. Давайте начнём с простого игрушечного примера: допустим, мы хотим считать три битовых поля, которые мы брали раньше:

    a = getbits(4);
    b = getbits(3);
    c = getbits(5);

Когда getbits реализован так, как выше, этот код будет проверять пополнение (и возможно сам процесс пополнения) до трёх раз. Но это глупо; мы заранее знаем, что будем считывать 4+3+5=12 бит за один раз, поэтому можем получить их все одновременно:

    refill(4+3+5);
    a = getbits_no_refill(4);
    b = getbits_no_refill(3);
    c = getbits_no_refill(5);

где getbits_no_refill — это ещё один вариант getbits, который выполняет peekbits и consume, но, как понятно из названия, без пополнения. И когда мы избавились от цикла пополнения между отдельными вызовами getbits, то у нас остался только прямолинейный целочисленный код, который хорошо оптимизируется компиляторами. Иными словами, случай с фиксированными длинами малозатратен; он становится ещё интереснее, когда мы не знаем, сколько битов мы на самом деле будем потреблять, например, как здесь:

    temp = getbits(5);
    if (temp < 28)
        result = temp;
    else
        result = 28 + (temp - 28)*16 + getbits(4);

Это простой код с переменной длиной, где значения с 0 по 27 передаются в 5 битах, а значения от 28 до 91 передаются в 9 битах. Смысл в том, что в этом случае мы не знаем заранее, сколько битов мы в дальнейшем потребим. Однако мы знаем, что их больше 9 битов, поэтому всё равно можем сделать так, чтобы пополнение происходило только один раз:

    refill(9);
    temp = getbits_no_refill(5);
    if (temp < 28)
        result = temp;
    else
        result = 28 + (temp - 28)*16 + getbits_no_refill(4);

На самом деле, если хотите, можно пуститься во все тяжкие и ещё больше разбить операции, чтобы оба пути выполнения только один раз потребляли (consume) биты. Например, при использовании битового буфера MSB-first, мы можем написать этот маленький декодер так:

    refill(9);
    temp = peekbits(5);
    if (temp < 28) {
        result = temp;
        consume(5);
    } else {
        // "Верхний" и "нижний" код стоят спина к спине,
        // и сочетаются идеально подходящим нам способом! Синергия!
        result = getbits_no_refill(9) - 28*16 + 28;
    }

Подобная микронастройка сильно не рекомендуется за границами очень нагруженных циклов, но как я упоминал выше, некоторые из этих циклов декодера достаточно нагружены, и в этом случае экономия нескольких инструкций в разных местах выливается в серьёзный выигрыш. Особенно важная техника декодирования кодов с переменной длиной (например, кодов Хаффмана) заключается в заглядывании вперёд на определённое количество бит с дальнейшим поиском в таблице на основании результата. В элементе таблицы указано, каким должен быть декодированный символ и сколько символов нужно потребить (т.е. какое число просмотренных битов на самом деле принадлежит символу). Это значительно быстрее, чем считывать код по одному-два бита за раз с проверкой на каждом этапе по дереву Хаффмана (к сожалению, этот метод предлагается во многих учебниках и других вводных текстах.)

Однако здесь есть проблема. Техника заглядывания вперёд и принятия решений о том, сколько бит нужно потребить, достаточно мощна, но мы только что изменили правила: показанная выше реализация getbits стремится считывать лишние байты только при крайней необходимости. Но наш изменённый пример считывателя кода с переменной длиной всегда пополняется, поэтому буфер содержит не менее 9 бит, даже если в конце мы потребим всего 5 бит. В зависимости от того, где происходит пополнение, это может даже привести к считыванию после конца самого потока данных.

Так мы познакомились с методом lookahead. Изменённый считыватель кода начинает получать дополнительные входные данные ещё до того, как будет уверен в их необходимости. Такой подход имеет много плюсов, но компромисс заключается в том, что он может заставить нас выполнить считывание за пределами логического конца битового потока; это подразумевает, что нам обязательно нужно обеспечить правильную обработку такого случая. Да, он может никогда не привести к сбою или считыванию вне пределов потока; но кроме этого он подразумевает принцип работы слоя буферизации ввода или кадрирования.

Если мы хотим выполнять заглядывание вперёд, то нам нужен какой-то способ обработки этого. Основные варианты таковы:

• Мы можем просто плыть по течению и сделать это чьей-то чужой проблемой, потребовав, чтобы все передавали нам правильные данные с дополнительными байтами-заполнителями после конца. Это упрощает нам жизнь, но неудобно для всех остальных.
• Мы можем организовать всё так, чтобы внешний слой кадрирования, передающий байты процедуре getbits, знал, когда заканчивается сам поток данных (благодаря или какому-то управляющему механизму, или явному заданию размера); затем мы можем или завершить выполнение заглядывания вперёд и при приближении к концу переключиться на более внимательный декодер, или заполнить поток каким-то пустым значением после завершения (чаще всего используются нули).
• Мы можем сделать так, чтобы какие бы байты мы ни получали во время lookahead при декодировании валидного потока, они всё равно оставались частью общего байтового потока, который обрабатывается нашим кодом. Например, если мы используем 64-битный битовый буфер, то можем обойти проблему, потребовав наличия сразу после битового потока какого-нибудь 8-байтного заполнителя (допустим, контрольной суммы или чего-то подобного). Поэтому даже если наш битовый буфер залез слишком далеко, то эти данные всё равно в результате будут потреблены декодером, что значительно упрощает логистику.
• В таком случае, любой слой буферизации ввода-вывода, который мы используем, должен позволить нам возвращать некие дополнительные байты, которые мы на самом деле не потребили в буфер. А именно, какие бы байты lookahead у нас ни остались в битовом буфере после завершения декодирования, их необходимо вернуть в буфер для того кода, который будет считывать его дальше. По сути, именно это делает функция стандартной библиотеки C ungetc, только мы не можем вызывать ungetc больше одного раза, а это может нам понадобиться. Поэтому выбор этого пути обрекает нас на внесение изменений в управление буфером ввода-вывода.

Я не буду утешать вас — все эти варианты сложно реализовать, и некоторые из них сложнее остальных: избавление от проблемы вставкой чего-нибудь в конце — самый простой способ; обработка ситуации в каком-то внешнем слое кадрирования — тоже неплохое решение, а переработка всего управления буферизацией ввода-вывода для отмены считывания нескольких байтов поистине ужасна. Но когда не может управлять кадрированием, хороших вариантов решения просто нет. В прошлом я писал посты об удобных техниках, способных помочь в этом контексте; в некоторых реализациях проблемы можно обойти, например, задав bitcount огромное значение сразу после вставки последнего байта из потомка. Но в общем случае, если вы хотите реализовать lookahead, то придётся вложить в него какие-то усилия. Тем не менее, выигрыш обычно стоит того, так что это не игра в рулетку.

Вариант 2: когда нам очень нужно считать 64 бита за раз

Все рассмотренные ранее методы используют различные хитрости, чтобы избежать работы с байтовой гранулярностью. Извлекающий читыватель битов начинает с считывания полных 64 битов, но затем ему приходится выполнять сдвиг на 7 позиций, чтобы отбросить уже потреблённую часть текущего байта, а показанный выше getbits1 вставляет в битовый буфер по одному байту за раз; если в буфере уже есть 57 битов, но для нового байта в нём нет места (потому что в результате получится 65 битов, что больше ширины буфера), поэтому такова максимальная ширина, поддерживаемая методом getbits1. 57 бит — это довольно полезный объём, но если мы будем работать на 32-битной платформе, то аналогичным волшебным числом будет 25 бит (32-7), и это довольно малая величина, которой часто недостаточно.

К счастью, если нам требуется полная ширина, существуют способы реализовать её (как и технике с поворотом и масками битовых буферов для MSB-first, я научился этому в RAD). Думаю, на этом этапе вы уже поняли соотношение между методами для MSB-first и LSB-first, поэтому я покажу решение только для одного варианта. Давайте выберем LSB-first:

// Инвариант: "bitbuf" содержит "bitcount" бит, начиная с
// LSB и вверх; 1 <= bitcount <= 64
uint64_t bitbuf = 0;     // значение битов в буфере
int      bitcount = 0;   // количество битов в буфере
uint64_t lookahead = 0;  // следующие 64 бита
bool     have_lookahead = false;

// Это необходимо сделать, чтобы запустить систему!
void initialize() {
    bitbuf = get_uint64LE();
    bitcount = 64;
    have_lookahead = false;
}

void ensure_lookahead() {
    // берёт слово lookahead, если
    // у нас его ещё нет.
    if (!have_lookahead) {
        lookahead = get_uint64LE();
        have_lookahead = true;
    }
}

uint64_t peekbits2_lsb(int count) {
    assert(bitcount >= 1);
    assert(count >= 0 && count <= 64);

    if (count <= bitcount) { // достаточно битов в buf
        return bitbuf & width_to_mask_table[count];
    } else {
        ensure_lookahead();

        // сочетаем текущий bitbuf с lookahead
        // (биты lookahead поступают в верхнюю часть текущего buf)
        uint64_t next_bits = bitbuf;
        next_bits |= lookahead << bitcount;
        return next_bits & width_to_mask_table[count];
    }
}

void consume2_lsb(int count) {
    assert(bitcount >= 1);
    assert(count >= 0 && count <= 64);

    if (count < bitcount) { // по-прежнему в текущем buf
        // просто сдвигаем биты
        bitbuf >>= count;
        bitcount -= count;
    } else { // всё из текущего buf потреблено
        ensure_lookahead();
         
        // мы полностью перешли на слово lookahead
        int lookahead_consumed = count - bitcount;
        bitbuf = lookahead >> lookahead_consumed;
        bitcount = 64 - lookahead_consumed;
        have_lookahead = false;
    }

    assert(bitcount >= 1);
}

uint64_t getbits2_lsb(int count) {
    uint64_t result = peekbits2_lsb(count);
    consume2_lsb(count);
    return result;
}

Такой подход чуть более сложен, чем рассмотренные нами выше, и требует этапа явной инициализации для правильной работы инвариантов. Также в отличие от предыдущих вариантов, в нём используется несколько дополнительных ветвлений, что делает его не слишком подходящим для машин с чётким конвейером, в том числе и для PC. Кроме того, заметьте, что я снова использую width_to_mask_table, и это не просто для демонстрации: никакие арифметические выражения, которые мы использовали в прошлый раз для вычисления маски заданной ширины, не работают для полного интервала 0-64 допустимой width в распространённых 64-битных архитектурах, кроме IBM POWER. Да и в ней она работает, только если мы будем игнорировать вызов неопределённого поведения, чего, разумеется, допускать нельзя.

Лежащая в основе идея довольно проста: вместо всего одного битового буфера мы отслеживаем два значения. Мы знаем, сколько битов осталось от последнего считанного 64-битного значения, и когда их недостаточно для peekbits, мы получаем следующее 64-битное значение из входного потока (с помощью реализованного внешне get_uint64LE()), чтобы получить биты, которых нам не хватает. Аналогично, consume проверяет, останутся ли биты в текущем входном буфере после потребления width бит. Если нет, то мы переключаемся на биты из значения lookahead (выполняя сдвиг на те из них, которые были потреблены) и сбрасываем флаг have_lookahead, чтобы указать, что бывшее значение lookahead теперь просто является содержимым битового буфера.

В этом коде присутствуют ветвления, чтобы гарантировать отсутствие сдвигов вне допустимого диапазона (которые вызывают неопределённое поведение). Например, посмотрите, как peekbits проверяет count <= bitcount, чтобы распознать случай наличия битов в буфере, а consume использует count < bitcount. Это не случайно: вычисление next_bits в peekbits включает в себя сдвиг вправо на bitcount. Поскольку это происходит только на пути, где bitcount < count ≤ 64, то значит bitcount < 64 и мы в безопасности. В consume ситуация обратная: мы выполняем сдвиг на lookahead_consumed = count - bitcount. Условие, окружающее блок, гарантирует, что lookahead_consumed ≥ 0; в другом направлении, поскольку count не больше 64, а bitcount не меньше 1, у нас получается lookahead_consumed ≤ 64 – 1 = 63. То есть, перефразируя слова Кнута, «опасайтесь багов в представленном выше коде; я всего лишь доказал его правильность, но не проверял его».

Кроме большей ширины битовых полей, эта техника имеет ещё один плюс: заметьте, что она всегда за раз считывает полные 64-битовые uint. Показанный выше вариант 1 считывает байты за раз, но требует цикла пополнения; различные варианты без ветвления, которые мы рассмотрим ниже, неявно полагаются на поддержку целевым процессором быстрых невыровненных считываний. Это единственная из версий, выделяющаяся считыванием одного размера и постоянным выравниванием, что делает её более привлекательной для целевых систем, не поддерживающих быстрые невыровненные считывания, например, для множества старых процессоров RISC.

Как обычно, существует куча других вариаций, которые я не буду показывать. Например, если у нас есть данные, которые мы полностью декодируем в памяти, то нет причин возиться с булевым флагом have_lookahead; можно просто хранить указатель на текущее слово lookahead, и увеличивать этот указатель при потреблении текущего lookahead.

Вариант 3: возврат к извлечению битов

Исходный считыватель битов с извлечением из предыдущей части был довольно затратным. Но если нас устраивает требование того, что весь входной поток одновременно находится в памяти, то мы можем обернуть его в паттерн refill/peek/consume, чтобы получить что-то полезное. У нас всё равно будет битовый считыватель, который заглядывает вперёд (а потому создаёт соответствующие сложности), но такова жизнь. Здесь мы для примера снова используем MSB:

const uint8_t *bitptr; // Указатель на текущий байт
uint64_t       bitbuf = 0; // последние считанные нами 64 бита
int            bitpos = 0; // сколько мы потребили из этих бит

void refill3_msb() {
    assert(bitpos <= 64);

    // Перемещаем указатель на количество полностью потреблённых бит
    bitptr += bitpos >> 3;

    // Пополнение (Refill)
    bitbuf = read64BE(bitptr);

    // Количество битов в текущем байте, которое мы уже потребили
    // (мы уже позаботились о полных байтах; здесь остатки битов,
    // которые не составляют полный байт.)
    bitpos &= 7;
}

uint64_t peekbits3_msb(int count) {
    assert(bitpos + count <= 64);
    assert(count >= 1 && count <= 64 - 7);

    // Избавляемся сдвигом от уже потреблённых битов
    uint64_t remaining = bitbuf << bitpos;

    // Возвращаем верхние "count" бит
    return remaining >> (64 - count);
}

void consume3_msb(int count) {
    bitpos += count;
}

На этот раз мы также отбросили getbits, построенный из вызовов refill / peek / consume, потому что это ещё один паттерн, который уже должен быть вам понятен.

Это довольно приятный вариант. Когда мы разбили логику извлечения битов на отдельные части «refill» и «peek»/«consume», то стало ясно, насколько малы и понятны эти отдельные куски. Кроме того, полностью отсутствует ветвление! Метод ожидает, что невыровненные 64-битные считывания big-endian существуют и достаточно малозатратны (это не проблема для распространённых архитектур x86 и ARM). Кроме того, для реалистичной реализации необходимо добавить обработку случаев конца буфера; см. рассуждения в разделе о «lookahead».

Вариант 4: другой тип lookahead

Теперь давайте реализуем ещё один вариант lookahead без ветвления. Насколько я знаю, этот вариант тоже был открыт с помощью RAD моим коллегой Чарльзом Блумом и мной при работе над Kraken (ОБНОВЛЕНИЕ: как указал в комментариях Yann, основная идея была использована в Xpack Эрика Биггерса ещё задолго до выпуска Kraken. Мне не было это известно, думаю, что и Чарльзу тоже, но это значит, что эта идея точно не пришла нам первым в голову. Однако у нашего варианта есть интересная особенность — подробности см. в моём ответе). Хотя все битовые считыватели без ветвления (в них нет ветвления, если мы игнорируем проверку конца буфера в refill и тому подобное), но этот вариант обладает некоторыми интересными свойствами (часть из них я обсужу позже, потому что пока нам не хватает нужных знаний), которые в таком сочетании я больше нигде не встречал; если кто-то другой опередил нас, то сообщите мне об этом в комментариях, и я обязательно упомяну авторов! Итак, здесь мы снова возвращаемся к LSB-first, потому что я пытаюсь показать вам, насколько взаимозаменяемы LSB-first/MSB-first на этом уровне, невзирая на все холивары.

const uint8_t *bitptr;   // Указатель на следующий байт для вставки в buf
uint64_t bitbuf = 0;     // значение битов в буфере
int      bitcount = 0;   // количество битов в буфере

void refill4_lsb() {
    // Получаем следующие несколько байтов и вставляем их прямо над
    // текущим верхним уровнем.
    bitbuf |= read64LE(bitptr) << bitcount;

    // Перемещаем указатель считывания для следующей итерации
    bitptr += (63 - bitcount) >> 3;

    // Обновляем количество доступных битов
    bitcount |= 56; // now bitcount is in [56,63]
}

uint64_t peekbits4_lsb(int count) {
    assert(count >= 0 && count <= 56);
    assert(count <= bitcount);
    
    return bitbuf & ((1ull << count) - 1);
}

void consume4_lsb(int count) {
    assert(count <= bitcount);

    bitbuf >>= count;
    bitcount -= count;
}

Мы уже видели ранее этапы peek и consume, однако на этот раз максимально допустимая битовая ширина по какой-то причине уменьшилась на единицу и составляет 56 бита.

Причиной является этап refill, работа которого слегка отличается от виденной нами ранее. Считывание 64 бит little-endian и их сдвиг для соответствия верхней части нашего текущего битового буфера вам должны быть уже понятны. Но манипуляции с bitptr / bitcount требуют объяснений.

Проще начать с bitcount. В вариантах, которые мы видели раньше, после refill в буфере обычно оказывалось от 57 до 64 бит. Однако эта версия нацелена на то, чтобы хранить в буфере от 56 до 63 бит (именно поэтому ограничение счётчика снизилось на единицу). Но почему? Вставка целого числа байтов означает, что во время refill bitcount будет увеличен на какую-то величину, кратную 8; это значит, что bitcount & 7 (нижние 3 бита) не изменятся. И если мы выполняем refill, нацеливаясь на [56,63] бит в буфере, то можем вычислить обновлённое количество битов единственной двоичной операцией OR.

Что приводит меня к следующему вопросу: на сколько байт нужно сдвигать указатель? Давайте просто посмотрим на значения в исходном bitcount:

• Если 56 ≤ bitcount ≤ 63, мы уже находимся в нашем целевом интервале и нам не нужно перемещаться на следующий байт.
• Если 48 ≤ bitcount ≤ 55, то мы прибавляем ровно 1 байт (и должны переместить bit_ptr на ту же величину).
• Если 40 ≤ bitcount ≤ 47, то мы прибавляем ровно 2 байта.

и так далее. Это работает с (63 - bitcount) >> 3 байтами, которые мы прибавляем к bitptr.

Для битов в bitbuf над bitcount операция OR может быть выполнена несколько раз. Однако когда такое случается, мы каждый раз применяем OR к одному и тому же значению, поэтому это не меняет результат. Следовательно, когда они в дальнейшем движутся ниже (из-за сдвига вправо в функции consume), с ними бывает всё в порядке; нам не нужно беспокоиться о возможности появления мусора.

Ну ладно, это конечно интересно, но что особенного в этом варианте? Когда его стоит использовать вместо, допустим, описанного выше варианта 3?

Есть одна простая причина: в этом варианте адрес, по которому выполняет загрузку refill, не имеет зависимости от текущего значения bitcount. На самом деле, следующий адрес загрузки становится известен сразу же после завершения предыдущей refill. Это небольшое отличие оказывается довольно большим преимуществом для процессоров с внеочередным выполнением. Среди операций с целыми числами, даже при попадании в кэш L1, операции загрузки отличаются высокими задержками (обычно около 3-5 циклов, в то время как большинство целочисленных операций занимает единственный цикл), а точное значение bitcount в конце итерации какого-нибудь цикла часто становится известным слишком поздно (см. простой код для переменной длины, который я показал выше).

Если адрес загрузки не зависит bitcount, то это значит, что потенциально команда загрузки может быть отправлена сразу же после завершения предыдущей refill; тогда у нас останется достаточно времени для завершения загрузки с возможной перестановкой байтов значения, если порядок следования байтов в load не соответствует целевой ISA (допустим, если мы используем битовый буфер MSB-first на little-endian ЦП). Единственным параметром, зависящим от предыдущего значения bitcount, является сдвиг, то есть обычная операция АЛУ, в общем случае занимающая один цикл.

Если вкратце подвести итог, то эта довольно запутанная версия refill выглядит странно, но обеспечивает гибкое повышение параллелизма на уровне инструкций. Когда я тестировал её в 2016 году в последней на то время версии декодера Kraken-Хаффмана, на настольных ПК повышение скорости составляло около 10% (по сравнению с предыдущей refill без ветвления, которая показана выше).

Автор: PatientZero

Источник