Офлайн А-Б тестирование в ритейле

Это реальная история. События, о которых рассказывается в посте, произошли в одной теплой стране в 21ом веке. На всякий случай имена персонажей были изменены. Из уважения к профессии всё рассказано так, как было на самом деле.

Привет, хабор. В этом посте речь пойдет про пресловутое А/Б тестирование, к сожалению даже в 21ом веке его не избежать. В онлайне уже давно существуют и процветают альтернативные варианты тестирования, в то время, как в офлайне приходится адаптироваться по ситуации. Об одной такой адаптации в массовом офлайн ритейле мы и поговорим, приправив историю опытом взаимодействия с одной топовой консалтинговой конторой, в общем го под кат.

Задача

В прошлом я работал на одном проекте в крупной компании, владеющей сетью продуктовых магазинов, более 500 магазинов. Боюсь, что мне не стоит называть имя компании, будем называть эту организацию Компанией. Суть в том, что магазины бывают разных размеров, могут отличаться размером в десятки раз; магазины могут быть в разных городах, селах и деревнях; магазины могут быть в разных районах города со своей демографией. Тут, в общем, я клоню к тому, что если нужно протестировать какую-либо гипотезу, то в парадигме А/Б тестирования это сделать почти нереально, не нанеся значительного ущерба бизнесу. Давайте все это дело рассматривать на примере пива. Однажды в Компанию приходит консалтинговая Контора, ну знаете эти, из самых самых топ и говорят: "а знаете ли, уважаемые, у вас тут пиво то не правильных марок на витринах, и вообще не в том порядке котором нужно, отгрузите нам пару камазов золота, и мы вам расскажем какие марки вам нужны, и как правильно их раскладывать, по нашим оценкам это принесет вам миллиард канадских долларов в первый год после пилота". Контора то уважаемая, так что сомнений по поводу миллиарда быть не может. Также не могут ставиться под сомнение методы Конторы, так как они не могут врать. Только не нам. В общем автору этих строк спускается задача вида "ну ты там посмотри как они пилот делают, помоги, если нужно будет им что".

Прослушав, небольшую лекцию о том, как работает их методика генерации выкладки товаров на витрину, желание, вдаваться в детали алгоритма, совсем пропало. Я решил сконцентрироваться на измерении качества, что с точки зрения теории значительно интереснее. А так же позволяет Компании не вкладываться в заведомо убыточные проекты. Имея доступ к параллельным вселенным, можно было бы провести А/Б тест, где во вселенной А все идет по старому, а во вселенной Б поменялась выкладка товара. А/Б тестирование является разновидностью контролируемого эксперимента, где пользователи случайно делятся на контрольную и тестовую группы. В тестовую группу делается вмешательство, выжидается какое-то определенное время, измеряется эффект такого вмешательства на целевые показатели, и наконец сравниваются показатели двух групп. Желательно, еще бы минимизировать смещение между контрольной и тестовой группой относительно друг друга. Например, чтобы не было такого, что в группе А присутствуют только города, а в группе Б только села. С сайтами вроде как вопрос о смещении решается легко: показывай пользователям с четным айдишником одну версию, а с нечетным другую версию сайта. В ситуации с сетью магазинов все не так просто, как бы ты не разбивал пользователей или магазины, всегда получается, что группы А и Б не похожи друг на друга. То группа А приходит в магазин днем, а Б вечером. Выравнив время, окажется, что А приходит по выходным чаще, чем Б. Выравнив все такие детали, окажется, что для статистически значимых результатов придется подождать пол года, и отменить все маркетинговые компании. Если бить по городам, то окажется, что Москва присутствует в одной группе и отсутствует в другой. В общем всегда наблюдается смещение одной группы относительно другой. На это все накладываются различные глобальные и локальные для магазинов маркетинговые кампании, праздники и непредвиденные обстоятельства в виде ремонта парковок.

Вы же помните, что Контора из самого топа мировых контор, и естественно у нее есть решение проблемы тестирования. Рассмотрим их методологию, с громким маркетинговым названием — методология тройной разности.

Методология тройной разности

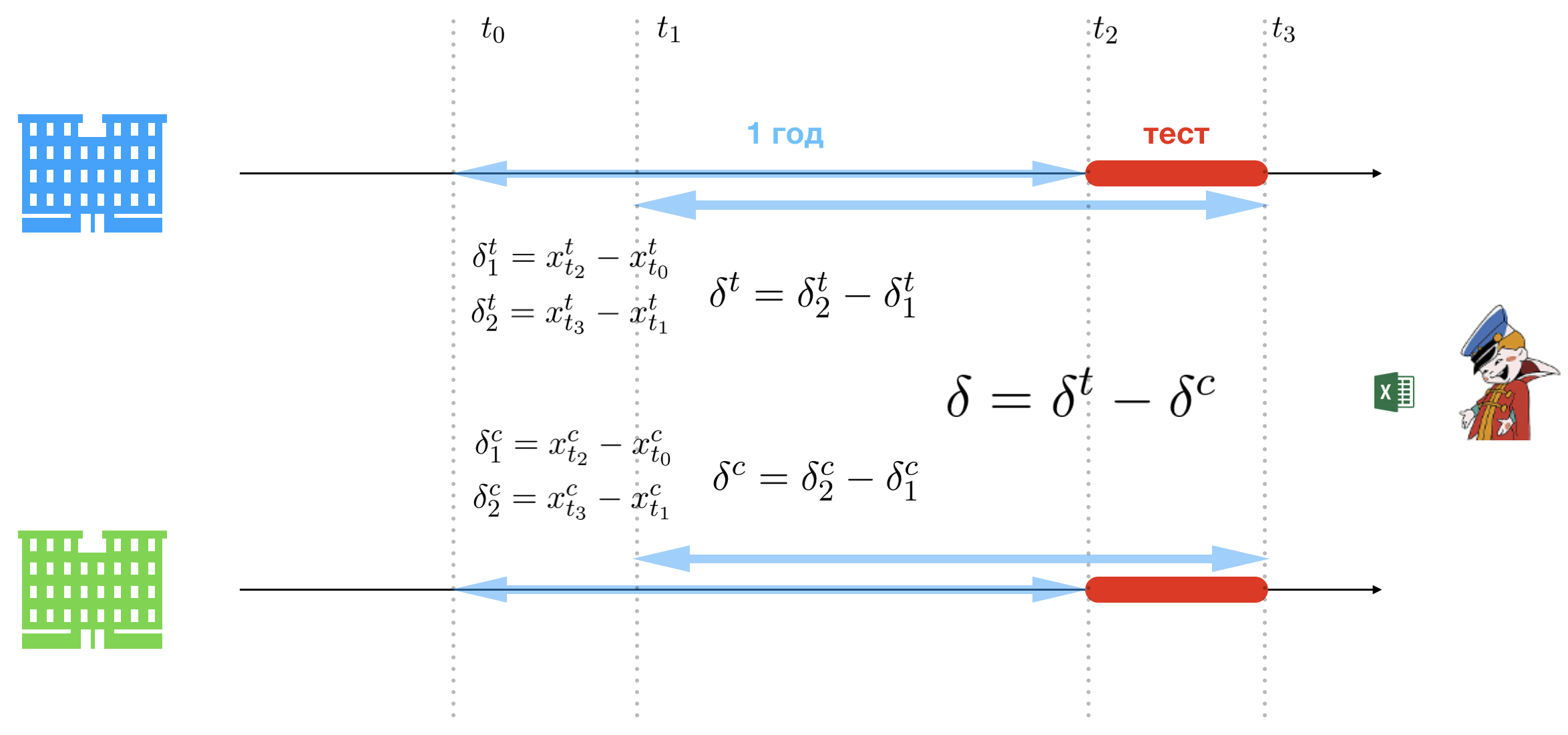
Суть методологии тройной разности в простоте. А чтобы топы Компании не напрягались при прослушивании презентации, эту презентацию будет вести леди недурной наружности. Простота достигается за счет релаксации ограничений накладываемых А/Б тестом. Единственная трудность которая остается на пути Конторы — это выбор контрольной и тестовой группы, но и эту часть процесса мы опустим, так как ничего интересного, кроме большого набора сомнительных предположений. Итак, в результате тщательного анализа существующей сети магазинов Контора выбирает два: один для контрольной группы (зеленый) и один для тестовой группы (синий).

Введем следующие обозначения:

• : дата начала пилота;
• : дата окончания пилота;
• : дата, соответствующая дате начала пилота в прошлом году;
• : дата, соответствующая дате окончания пилота в прошлом году.

Таким образом у нас есть два периода времени:

• : период пилота (период проведения эксперимента);
• : период, соответствующий периоду пилота в прошлом году.

Предлагается сравнить доходы тестового магазина и контрольного на периодах пилота и год назад. Для этого нужно посчитать три группы разностей. Обозначим продажи в день в тестовом магазине за , а — в контрольном. Группа первая, задает базисную линию от которой будет измеряться рост или падение продаж в пилотный период:

• : разница в продажах между началом пилота и той же датой год назад в тестовом магазине;
• : разница в продажах между окончанием пилота и той же датой год назад в тестовом магазине;
• : разница в продажах между началом пилота и той же датой год назад в контрольном магазине;
• : разница в продажах между окончанием пилота и той же датой год назад в контрольном магазине.

Вторая группа разностей, задает рост или падение продаж в пилотный период:

• : разница в продажах между окончанием пилота и началом пилота в тестовом магазине (скорректированная относительно дат год назад);
• : разница в продажах между окончанием пилота и началом пилота в контрольном магазине (скорректированная относительно дат год назад).

И наконец решающая разность, определяет какой магазин отработал лучше в пилотный период:

• 

Ну и решение о внедрении проекта стоимостью камаз золота определяется очень просто, если — значит тестовый магазин продал больше пива, следовательно методика Конторы работает и дает положительный эффект, следовательно нужно внедрять. Все.

А/Б тест с МЛ бейзлайном

Изучив методологию тройной разности и узнав, что начальство уже одобрило такой метод измерения и начало планировать пилот, моя рука больно ударила меня по лицу. Получается контора предлагает нам вложить камаз золота в проект, даже в случае если методология не работает, а разница в продажах была в 1 рубль, по какой-то случайности. Нужно было срочно разработать, что нибудь, что давало бы хоть какую-то уверенность в эффективности нового способа выкладывания пива на полку. Как вы помните, что один из способов провести честный А/Б тест в офлайне — это существование параллельных вселенных, тогда в одной мы можем внедрить методологию выкладки пива, во второй оставить все как есть, подождать некоторое время и сравнить результаты. А что если смоделировать параллельные вселенные машинным обучением?

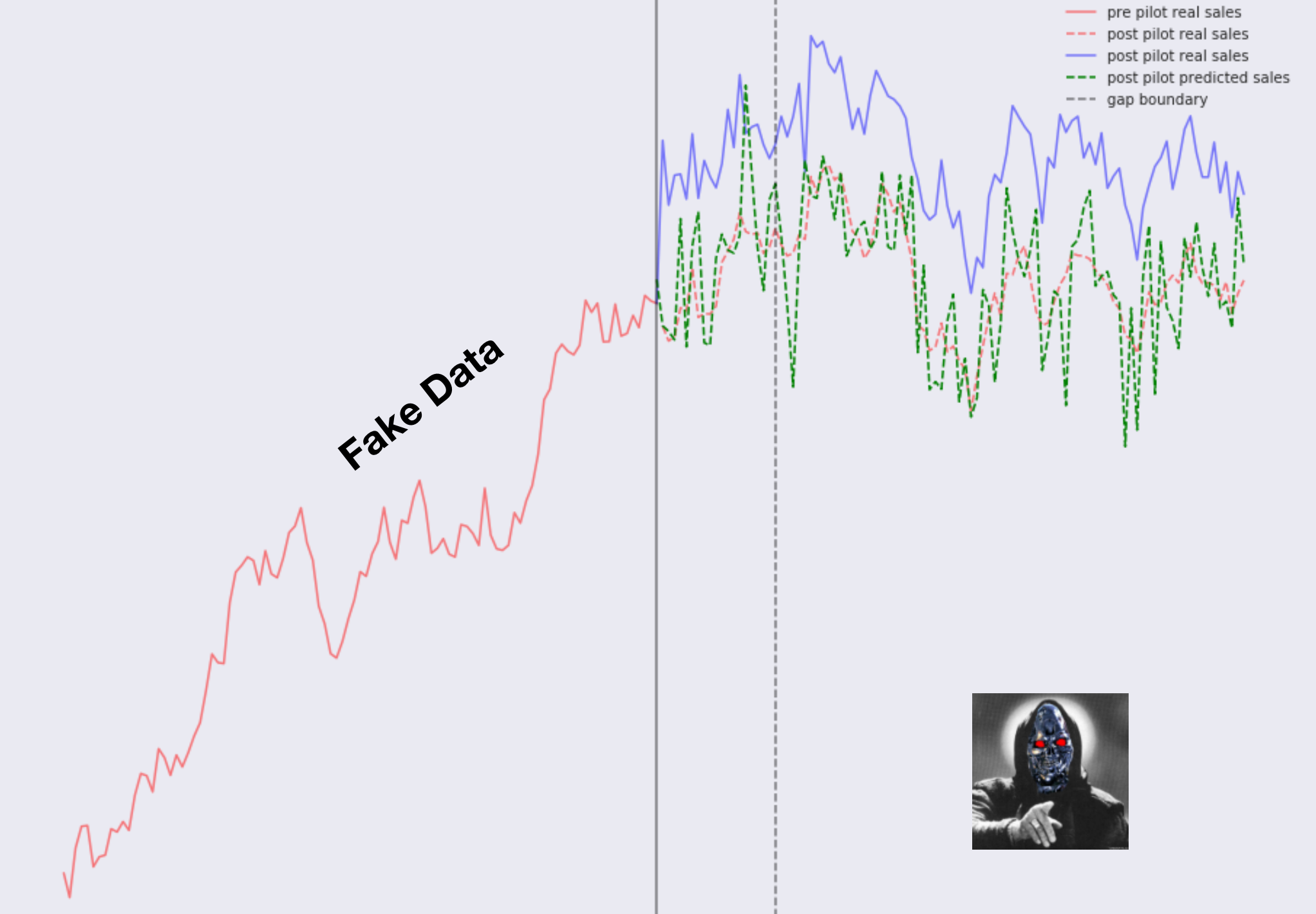
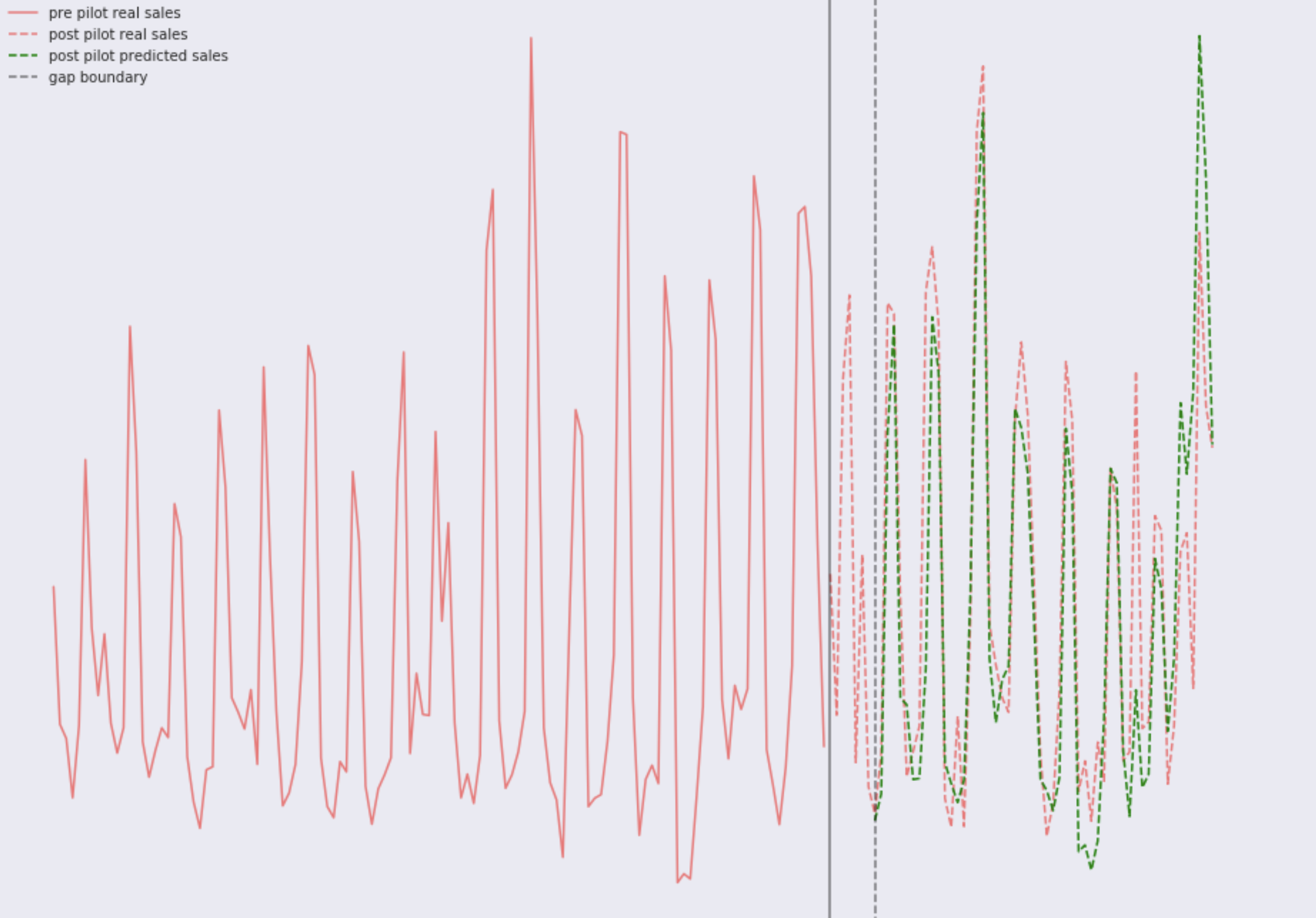
Допустим у нас есть временной ряд дневных продаж на каждый магазин. Серая сплошная линия разделяет периоды до пилота и после пилота. Зона между сплошной серой линией и прерывистой серой линией — это период адаптации покупателей к новой выкладке товаров и новым брендам, в этот период данные о продажах не влияют на результат теста и просто игнорируются. Красная сплошная — это реальные продажи любого магазина в период до пилота. В правой части комбинация тестовых магазинов и контрольных. Зеленая прерывистая линия — это прогноз продаж любого магазина, используя только данные доступные в период до запуска пилота.

• Красная линия — это реальные продажи контрольного магазина в период после запуска пилота. Для магазинов из контрольной группы, в период после старта пилота, мы наблюдаем только прогноз продаж (зеленая прерывистая) и реальные продажи (красная прерывистая).
• Синяя сплошная — это реальные продажи магазина из тестовой группы в период после запуска пилота. В тестовых магазинах мы наблюдаем только прогноз продаж (зеленая прерывистая) и реальные продажи (синяя сплошная).

Зеленая прерывистая линия и есть бейзлайн на машинном обучении.

Если пилот был успешный, т.е. тестовое вмешательство в виде обновленного ассортимента и новой выкладки имеют положительный эффект на дневные продажи, то реальные продажи в тестовых магазинах (синяя сплошная) будут в среднем выше чем реальные продажи в контрольных магазинах (красная прерывистая).

Давайте разберемся, что же значит в среднем. Для этого придется сделать одно предположение, будем считать, что ошибки прогноза модели имеют нормальное распределение:

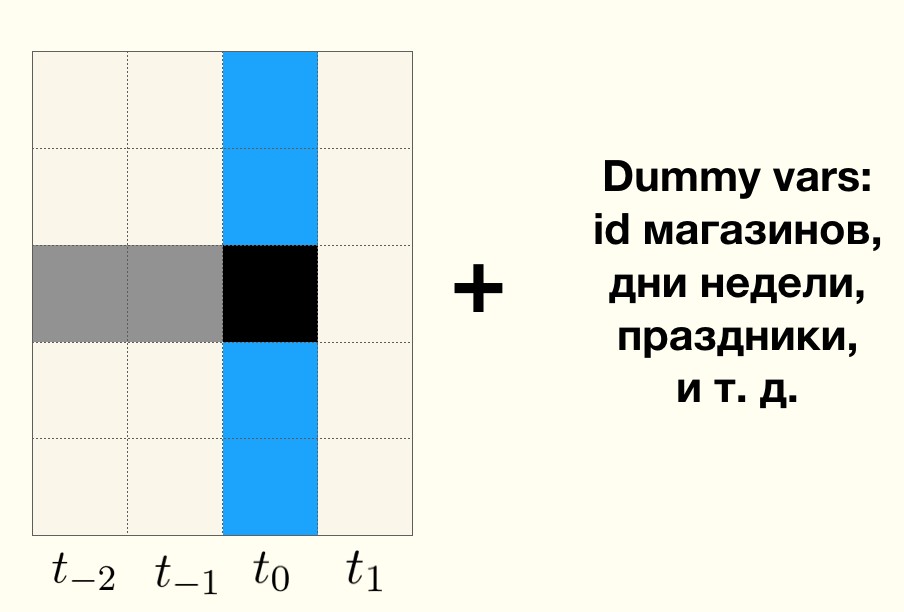Давайте добавим еще одно смелое предположение, допустим продажи в интересующей нас категории сегодня линейно зависят от продаж в смежных категориях сегодня и продаж в интересующей нас категории вчера и в некотором недалеком прошлом, а так же к этому всему можно приписать различные метаданные магазинов, чтобы учесть смещения в демографии и других признаках.

Получается уж очень знакомая модель. Тут стоит отметить, что выбор модели тут не особо существенен, важно, чтобы ошибки имели нормальное распределение, или другое известное, для того, чтобы провести статистический тест на равенство средних значений. При таких постановках задачи, всегда можно провести тест на нормальность на этапе построения модели, и почти на любых моделях распределение будет нормальным, по версии статтеста на нормальность, проверено.

Итак, в качестве прогнозирующей модели я использовал линейную регрессию, хотя это не обязательное требование, а я руководствовался простотой модели и интерпретируемостью. Стоит отметить, что модель прогнозирующая, но я бы назвал ее объясняющей. Так как в мы не прогнозируем будущее, мы ведь используем продажи из смежных категорий в тот же день, что по сути является даталиком. Скорее мы пытаемся объяснить продажи пива сегодня, продажами в магазине в целом. Это создает нам новую проблему — необходимо тщательно отобрать признаки, используемые в модели. Признаки, относящиеся к категориям смежных товаров, можно разбить на три группы:

• группа интересующих нас товаров (пиво светлое, пиво темное, нулевочка, квас, может даже желтый полосатик), часть таких признаков формируют целевую переменную, а часть исключается из модели совсем;
• группы товаров, которые скорее всего кое как скоррелированы с целевой группой, например баянистая история про то, что продажи памперсов и пива имеют высокий положительный коэффициент корреляции;
• группы товаров, который ну уж точно не имеют существенной корреляции с целевыми группами, это такой способ регуляризации еще до построения модели, и тут вот будет большой соблазн добавить все во вторую группу, на всякий случай.

В модель в качестве объясняющих переменных мы добавляем признаки из второй группы. Идея заключается в том, что мы предполагаем, что изменения в продажах во второй группе в целом имеют значительный эффект на первую, а изменения в продажах в первой, не имеют особого эффекта на вторую целиком (вторая значительно больше и вариативнее).

Популярный вопрос в процессе презентации метода был такой: а что если в тестовом/контрольном магазине будет ремонт парковки, тест сломается? Ответ — нет. Парковка повлияет на продажи магазина в целом, а не конкретно на пиво, а продажи пива у нас зависят от продаж в других категориях и соответственно просядут вместе со всеми. Можно для убедительности провести пару симуляций на ретродатке.

Так же стоит отметить, что мы не тестируем выкладку методом А против выкладки методом Б, а тестируем новое поведение против старого. Это значит, что магазины и группа в целом не должны отменять никаких запланированных маркетинговых кампаний, из тех, что раньше применялись. Например если вы в течении последних 6 месяцев, по четным неделям снижали цены на крепкое пиво в 2 раза — продолжайте это делать, если вы это перестанете делать, то поведение будет другим. Воздержаться стоит только от проведения новых экспериментов в выбранных магазинах.

Этап построения модели тоже не обойдется без подводных камней. В тестовую и контрольную группу могут входить совершенно разные магазины, а задача нашей модели выровнить все магазины, так чтобы для любого магазина, случайная ошибка прогноза была центрирована в нуле (или одинаково смещена относительно нуля). Я по начала ожидал, что придется перебирать на валидации всевозможные гиперпараметры, пока не получится нужного результата. Но оказалось, что при достаточном наборе признаков, это достигается с первого раза, что интересно, и дисперсия случайной ошибки тоже не сильно отличалась от магазина к магазину. Вероятно это одно из самых слабых мест метода, так как нет никакой гарантии что такие условия будут выполнены. Обзор литературы тоже не дал никаких результатов, вроде много где применяют бейзлайн на машинном обучении, но нигде нет ничего про теоретические гарантии. В общем после всех таких махинаций мы получаем модель, которая обучается на всех даных целиком, а мы можем делать прогнозы дневных продаж для любого выбранного магазина. Причем нас не особо волнует точность, а лишь бы распределение ошибки для всех магазинов было одинаково смещено (приятнее конечно, если не смещено относительно нуля). А то что дисперсия может быть большой, это уже повлияет только на размер датасета, требуемого для статистической значимости результата теста (имеется в виду, что при заданных априори статистической значимости и статистической мощности теста, количество наблюдений. требуемый для получения таких результатов, зависит от дисперсии).

Вернемся к графику выше с красной, зеленой и синей линиями, и наконец введем понятие в среднем выше или ниже. Для контрольных магазинов мы можем вычесть из реальных дневных продаж (красная прерывистая линия) дневные продажи предсказанные моделью (зеленая прерывистая). В результате мы получим нормальное распределение ошибок с центром в нуле, так в них ничего не менялось и модель будет в среднем совпадать реальностью. Для магазинов из тестовой группы мы также вычитаем из реальных дневных продаж (синяя сплошная линия), дневные продажи модельные продажи (зелена прерывистая), и тоже получаем нормальное распределение. Тогда если ничего не изменилось, то центр будет где-то около нуля; если продажи улучшились, то будет смещено вправо, если ухудшились — то влево. Так это выглядит на симулированных данных.

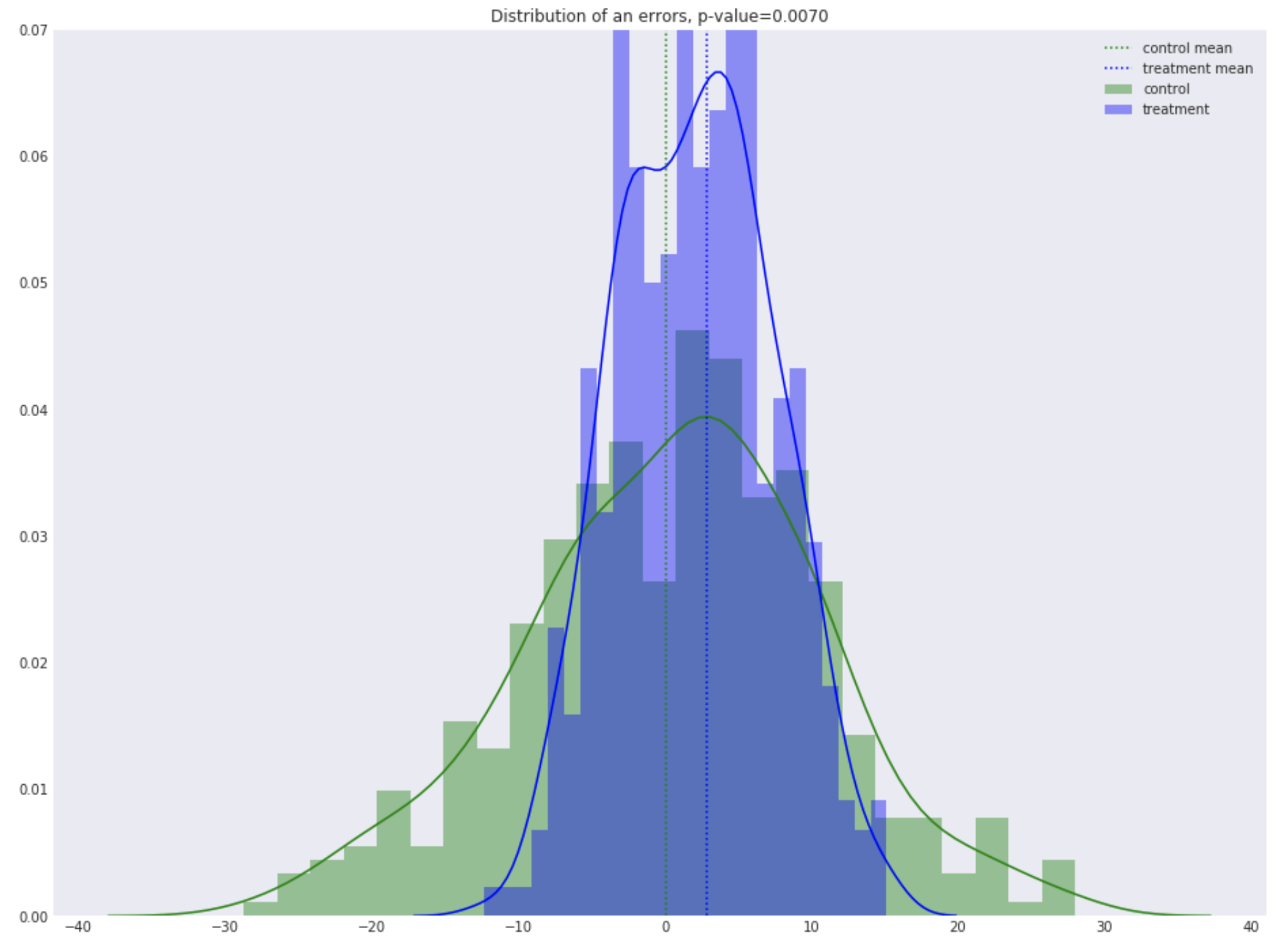
И вот тут-то мы попадаем в условия обычного статистического теста на равенство средних двух распределений, и ничто не мешает нам провести этот тест. Для статтеста нам необходимо знать следующее:

• и : выбираем сами, или если вам повезло и в маркетинге сидят образованные люди, то выбираем вместе с ними;
• дисперсия: берется из ретродатки;
• лифт: нужен чтобы тестировать не просто на равенство, а на то, что прирост продаж в тестовой группе не менее чем на определенное количество условных канадских долларов; мы ведь не хотим внедрять проект стоимостью в камаз золота, но так чтобы он был рентабельный и окупался не за сто лет, не мост в Крым же строим.

Этих данных будет достаточно, чтобы вычислить необходимое количество дней, необходимых для проведения пилота. Еще одним бонусом такого подхода является масштабируемость. В нашем случае тест выдал 60 дней, т.е. нам необходимо 60 дневных наблюдений для тестовой и 60 дневных наблюдений для контрольной групп, чтобы получить статистически значимые результаты теста. Мы можем выбрать по одному магазину в каждую группу и ждать 2 месяца, либо по два в каждую группу и ждать 1 месяц, и так далее. Естественно от добавления в тестовую группу новых магазинов зависит бюджет эксперимента, но это уже ваша задача как выбрать такое равновесие. Рекомендую изучить этот материал, для того, чтобы понять методику вычисления необходимого количества наблюдений.

Реальные данные

Рассмотрим два изображения с реальными продажами, модель обучена на нескольких годах ретроданых. Магазин номер один:

И магазин номер два:

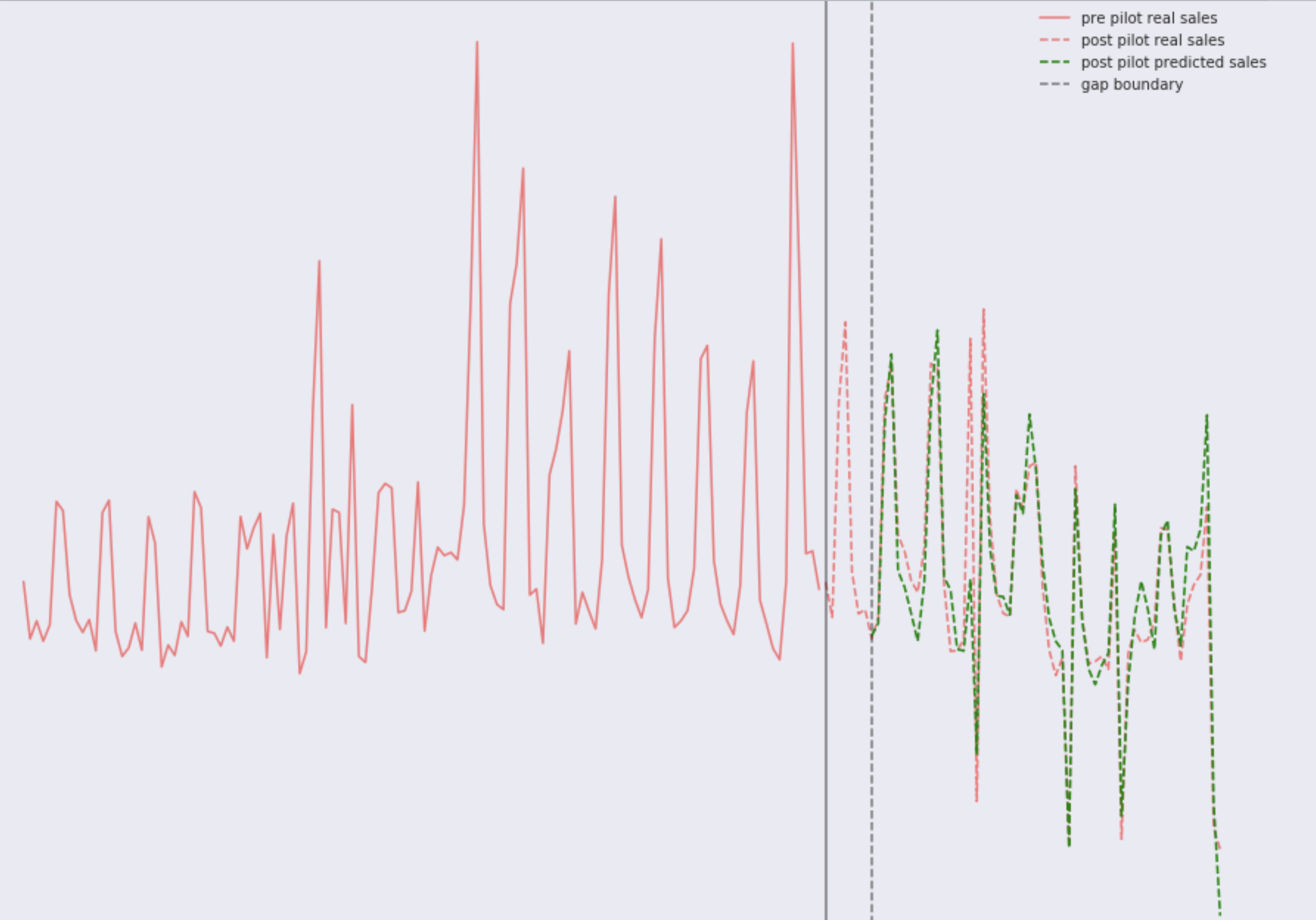
Как видите на глаз все очень даже хорошо. Вы легко заметите недельные паттерны, а так же в одном из магазинов недавно явно что то произошло, динамика изменилась. Если внимательно присмотреться, то видно, что модель в обоих магазинах по несколько раз делает значительную ошибку. В таком случае варианта два:

• вернуться на шаг отбора признаков и найти признак, который объяснит это поведение, вероятно какая то компания;
• применить детектор аномалий и выкинуть их рассмотрения те дни, в которых наблюдается аномальная ошибка; если ошибка будет систематическая, то они естественно не будут считаться аномалиями; так же выкидывание легко объясняется бизнесу, так как нововведение в виде выкладки пива должно иметь систематический характер, а не так, что в один какой то конкретный день, продажи скакнули, а в остальные дни не менялись.

Рассмотрим распределение ошибок для двух контрольных магазинов и одного тестового:

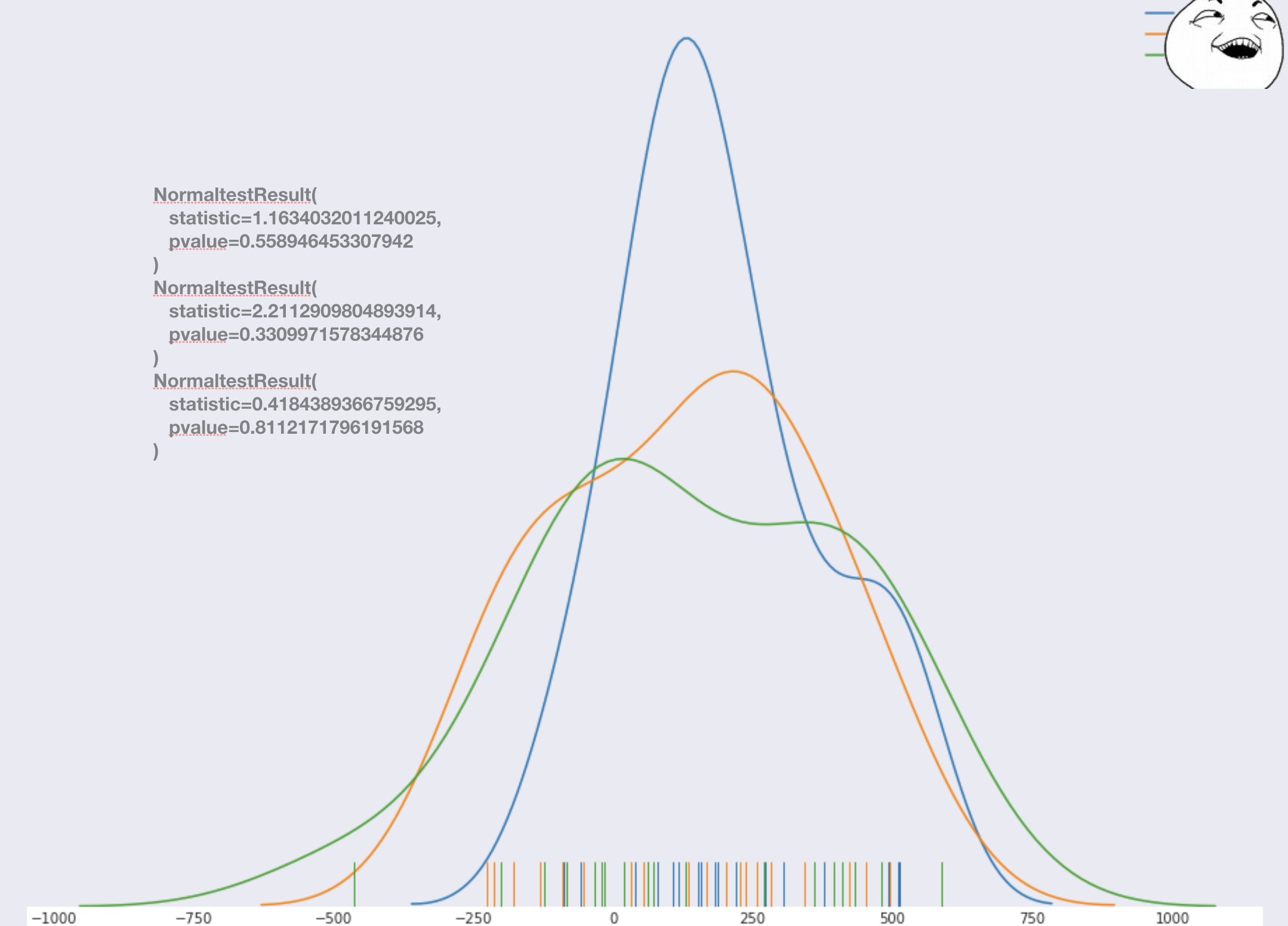
Выглядит нормально. Для убедительности можно провести тест на нормальность, и убедиться что все нормально. Если же какой то тест будет выдавать не нормальные результаты, то либо забить, либо откатываться на пункт выбора признаков. В таком случае, нам же не нужно перезапускать пилот, а только перестроить модель и пересчитать цифры (так что заранее можно подумать о том, чтобы включить чуть больше пилотных дней в тестовый период, чем выдает первая версия модели). В нашем случае все было как нужно.

Далее объединяем все магазины тестовой группы в одну группу и все магазины контрольной в одну группу, чтобы можем делать, так выше мы предположили, что ошибка модели одинаково смещена для любого магазина. Получаем два распределения и проводим статтест.

Как вы могли уже догадаться, по моему скептицизму в самом начале, новая уникальная методика выкладки товара и подбора брендов не имела никакого статистически значимого эффекта на продажи. Что в принципе было ожидаемо, так как я видел методику выбора новых брендов и способа их выкладки. Боюсь, что я не могу рассказывать про эти уникальные методики, но один из фотографов, который ходил к конкурентам фоткать витрины с пивом получил… был в грубой форме выдворен из помещения.

Заключение

Резонный вопрос может возникнуть — а зачем вообще контрольная группа? Она нам нужна только для того, чтобы учесть какие то глобальные изменения, так как пилот может длится 1-2 месяца. Данный метод можно модифицировать для тестирования промо-акций длительностью в неделю, например — распродажа сосисок. Если мы считаем, что за неделю никаких глобальных изменений скорее всего не будет, тогда тестируется тестовая группа против модели, которая и выступает контрольной, а статтест проводится на равенство нулю среднего значения распределения. Проиллюстрируем это следующим образом:

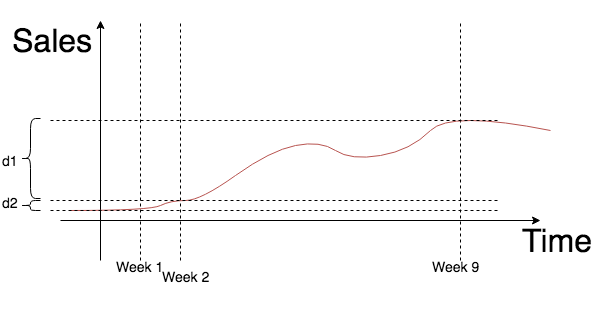
• время по оси абсцисс и продажи по оси ординат;
• показывает рост продаж в первую неделю под эффектом глобального роста экономики, например;
• показывает рост продаж в остальное время под эффектом глобального роста экономики.

Описанный пилот может длиться несколько месяцев, а вот различные промо-акции обычно короткие, около недели. Если мы можем игнорировать ожидаемый , например потому, что ожидаемый лифт сильно выше, то контрольная группа нам не понадобится, и уйдет в ошибку прогноза. Если же мы не можем игнорировать , то нам понадобится контрольная группа, так как мы будем совершать одну и туже ошибку в обеих группах, они будут одинаково смещены, и ошибки нивелируют друг друга.

А что же стало с пилотом? А все ок, идет и процветает, ждут миллиард взамен отданного камаза золота. Одной из последних задач на проекте было как раз внедрение методологии тестирования промо-акций, но как я ушел с проекта уважаемая Контора быстро вернула тест на подобие тройной разницы. Наверное та же участь постигла и этот тест, но я не в курсе.

Кстати, сейчас успешно внедряется в другом ритейле, тестируется оптимизация ассортимента, предложенная еще одной консалтинговой конторой, но не этой Конторой. Результаты оправдали ожидания клиента и конторы, и клиент планирует внедрить новую оптимизацию ассортимента на основе результатов такого теста.

Автор: Павел Нестеров

Источник