Создаем калькулятор с единицами измерений

Как-то раз мне нужно было реализовать калькулятор для складывания и конвертации физических величин. У меня тогда не было ограничений по времени, поэтому я решил проблему на высоком уровне абстракции и, соответственно, под широкий спектр задач. Предлагаю на ваш суд мое решение.

Представьте, что вам нужно написать калькулятор, который умеет не просто считать цифры, а оперировать физическими (измеряемыми) величинами – складывать длину, конвертировать количество чего-то из одной единицы измерения в другую, и т.п. Первым делом, давайте обозначим чуть конкретнее задачу. У нас будут вот такие фичи:

• Калькулятор должен поддерживать условно любую математическую операцию, т.е. понятие операции должно быть своего рода интерфейсом, чтобы при необходимости их можно было добавлять. Но для начального этапа давайте остановимся на следующем перечне:
  • Сложение/вычитание
  • Умножение/деление
• При работе с калькулятором, мы хотим полностью переложить на плечи калькулятора вопросы конвертации единиц измерений. Отсюда следует 2 вещи:
  • До тех пор, пока запрашиваемая операция имеет физический смысл, калькулятор должен сам понимать, как ему конвертировать операнды для выполнения математической операции. К примеру: 10 футов + 5 метров (складываются 2 длины) или 10 ньютонов * 1 дм (если помните физику, то тут результат должен быть в Джоулях).
  • Если же с физической точки зрения запрашиваемая операция бессмысленна, то даже при наличии математического смысла, нужно отказываться от ее выполнения. К примеру, 10 метров + 5 кг с физической точки зрения – полный нонсенс, хотя математически мы еще как-то могли бы сложить 10 и 5.
• Хоть какая-то производительность: на выборках размера 10-100 тыс. выражений калькулятор должен отрабатывать за доли секунды.
• Конкретная задача, под которую я искал решение, требовала сохранять “измеряемые значения” в БД.

Анализ предметной области

В процессе анализа я буду двигаться от общего к частному.

Прежде всего видно, что тут есть своего рода два измерения – физика и математика. Для физики важна размерность каждого из операторов. Ведь 5 метров / 2 секунды это не 5 кг / 2 м2 ибо единицы измерения отличаются. А для математики 5 метров * 100 отличается от 5 км * 0.1, т.к. там разные цифры фигурируют.

Начнем с того, что введем понятие выражения. Пускай это будет нечто, чем будет оперировать калькулятор. Простейшими выражениями могут быть вещи из разряда 5 метров, 45 (просто безразмерная константа) и т.д. Но выражения могут быть и более сложными: 10 метров + 2 см или 5 кг * 45.

Как бы там ни было, любое выражение должно знать (либо уметь находить) 2 своих свойства:

1. абсолютную величину (математика)
2. размерность (физика)

Абсолютную величину можно найти, приведя единицы измерений к их SI базовой единице и посчитав циферки. Для выражения 10 км / 3 часа абсолютная величина будет ~1.39: 10 км / 3 часа = 10000 м / 7200 с = 1.39 м/с. Ну и физическая размерность уже очевидна: м/с.

А для выражения 5 * 2, абсолютная величина 10, физическая размерность нуль (ничего).
За счет операторов (действий) мы из простых выражений можем строить более сложные и сложности этой нет предела.

Физическая размерность

Для нас интуитивно понятно, что 2 км и 2 м2 / 10 см обладают одинаковой размерностью — метры. А как это объяснить компьютеру? Для начала нам потребуются базовые физические измерения. Не будем изобретать велосипед и возьмем SI единицы измерений как базовые:

• длина, м
• масса, кг
• время, с
• … этот список можно продолжать, вводя новые измерения (электрический заряд, температура, и т.д.), но для простоты нашего анализа, давайте остановимся на первых трех.

Тогда размерность любого выражения можно представить в виде вектора размерности. Длинна такого вектора размерности будет равняться количеству известных базовых единиц измерений. Значение напротив каждого из базовых измерений будет показывать степень размерности по этому измерению.

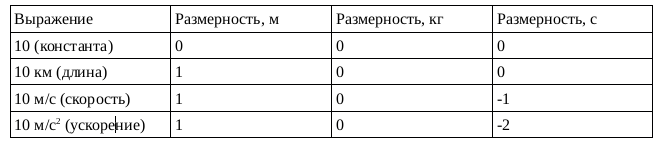
Тогда с позиции физики мы всегда смотрим на размерность (вектор размерности) выражений. Например: 10 км или 1 м – вектор размерности у обоих выражений одинаковый, хоть они и используют две разные единицы измерений.

С математикой (абсолютное значение), надеюсь, сильно объяснять не нужно – просто считаем циферки, как на обычном калькуляторе.

Комплексные единицы измерений

Нам еще нужно научиться раскладывать комплексные (небазовые) единицы измерений на базовые – будет полезно как для физики (а ну-ка, назовите мне вектор размерности 1 Джоуль) так и для математики (какова будет абсолютная величина 8 км).

Представьте, что у нас будет справочная таблица, где ключом будет единица измерений, а значением выражение, которое эту единицу измерений расщепляет на базовые, сохраняя размерность и абсолютное значение оригинальной комплексной единицы измерения.

Соответственно, если единицы измерений нет в справочной таблицы – значит такая единица уже является базовой (неразложимой) а посему – входит в вектор размерности. Давайте назовем такую справочную таблицу таблицей декомпозиции, т.к. она объясняет как можно декомпозировать комплексные единицы измерений в базовые.

Обратите внимание, что декомпозиция может происходить как на физическом уровне (Ньютон декомпозируется исключительно в другие единицы измерений, по абсолютной величине он не меняется), так и математически (километр декомпозируется в свою базовую единицу измерений и “корректируется” численно).

Публичный (высокоуровневый) интерфейс

Вот мы уже нащупали определенные абстракции, которые прячутся за задачей. Теперь давайте придумаем интерфейс, который мы хотим предоставить наружу, и который наш калькулятор обязуется реализовать. В этом месте важно спроектировать интерфейс так, чтобы он был элегантным, легким к пониманию и использованию снаружи.

Безусловно, в центр сцены нужно ставить нашу абстракцию выражение. На вход калькулятору будут даваться какие-то сложные выражения с умножением, суммой и т.д., а на выходе он должен давать эквивалентное выражение, которое уже посчитано и приведено к максимально простой форме.

Интерфейс выражения

Какие методы нам потребуется в этом интерфейсе выражение? Я предлагаю следующие:

• dimension() : Dimension получить вектор размерности нашего выражения. Мы его будем внутренне использовать для валидации физического смысла (мухи можно складывать только с мухами). Будет полезно дать его “наружу” как часть публичного интерфейса, т.к. весьма логично, что кто-то рано или поздно захочет узнать размерность какого-нибудь выражения.
• evaluate() : float Расчитать абсолютное значение выражения, т.е. посчитать “математику”.
• decompose() : MathematicalExpression разложить все комплексные единицы измерения в выражении на их декомпозицию. Нам этот метод будет полезен как для вычисления абсолютного значения, так и для расчета вектора размерности. Но опять же, звучит весьма логично включить эту операцию в наш публичный интерфейс ведь кому-нибудь такая операция может понадобиться за пределами внутренней реализации нашего калькулятора.
• formatQuantity(float $quantity) вписать в наше выражение константы (и подобрать эти константы) так, чтобы численно выражение начало равняться $quantity. Такой метод будет чуть гибче, чем просто конвертация из одной единицы в другую. Вот пример: американцы используют футы и дюймы для человеческого роста. У меня рост 180 см. Я мог бы сконвертировать это в футы (5.905512) либо в дюймы (70.8661457). Но для американского мозга каноничный вид – это выделить полные футы и остаток записать в виде дюймов – 5 дюймов 10.8 дюймов. Тогда снаружи можно представить себе следующий псевдо-код для форматирования/конвертации (может быть на 2-3 строчки больше кода, но гибкость конструкции на порядок выше):

  $quantity = $source_expression->evaluate();
  $european_height = new MathematicalExpression(“1 * meter”);
  $european_height->formatQuantity($quantity);
  print $european_height->toString() . “n”; // 1.8 * meter
  $us_height = new MathemticalExpression(“1 * foot + 1 * inch”);
  $us_height->formatQuantity($quantity);
  print $us_height->toString() . “n”; // 5 * foot + 10.8 * inch

Заметьте, мы можем утверждать, что два выражения равны тогда и только тогда, когда их векторы размерности равны, и когда их абсолютное значение одинаковое. Вот примеры:

• 100 м и 0.1 км равны, т.к. у обоих размерность метра и абсолютная величина равняется 100.
• 100 м и 100 кг не равны, т.к. у них физическая размерность отличается.

Интерфейс размерности

Еще у нас есть понятие вектора размерности. Было бы неплохо ввести некоторый интерфейс для работы с размерностями. Нам будет уместно определить следующие операции на векторах размерности:

• addDimension(Dimension $dimension1, Dimension $dimension2) : Dimension Сложить одну размерность с другой. Банально выполняем векторное сложение/вычитание. Это будет полезно при операциях умножения, когда размерности складываются.
• subtractDimension(Dimension $dimension1, Dimension $dimension2) : Dimension Вычесть одну размерность из другой. Аналогично с предыдущей операцией, только инвертируется знак. Будет полезно, когда обрабатывается операция деления.
• isEqual(Dimension $dimension1, Dimension $dimension2) : bool Сравнить одну размерность с другой. На этом методе будет основываться вся логика валидации физических размерностей. С помощью этой функции мы поймем, имеет ли физический смысл складывать/вычитать два выражения.

Интерфейс оператора

Я уже упомянул, что нам потребуется понятие математической операции. Пришло время рассмотреть его в деталях. Прежде всего, мы уже обусловились, что “рабочая лошадка” нашего калькулятора – это интфрейс выражения. Наш калькулятор безусловно должен уметь полноценно работать с операторами, из этого следует, что интерфейс оператора должен расширять интерфейс выражения. Кстати, это весьма логично! Если 10 м – это выражение, то почему бы 10 м + 20 см не быть выражением?

Это значит, что операторы должны уметь расчитывать свою размерность, расчитывать свое абсолютное значение, и прочий функционал, подразумеваемый интерфейсом MathematicalExpression.

Но операторы явно чуть больше, чем просто выражение. Давайте еще добавим в интерфейс оператора следующие методы:

• operand1() : MathematicalExpression получить первый (левый) операнд
• operand2() : MathematicalExpression получить второй (правый) операнд

Опять же, логично дать возможность кому-то снаружи исследовать левый и правый операнд на случай, если кто-то захочет каким-то образом анализировать уже существующее выражение. Это хороший пример полного интерфейса – я не знаю для чего кому-то может понадобиться левый и правый операнды, но это чертовски звучит как неотъемлемая часть интерфейса оператора.

Распределение обязанностей между слоем приложения и БД

В постановке задачи мы согласились, что будем хранить эти выражения в БД, и что система должна быть производительна на масштабе десяток-сотен тысяч выражений. Это значит, что сортировка по абсолютному значению должна выполняться внутри БД. В противном случае мы будем очень медленны.

Тут буквально три пункта, которые нужно проговорить:

• Логика валидации данных должна быть на уровне приложения. У нас вся валидация сводится к тому, что выражение должно иметь физический смысл, т.е. размерности не противоречат друг другу. Слой приложения не должен записывать в БД выражение, которое не имеет физического смысла. Из этого следует, что на уровне БД нам не нужно заморачиваться по поводу размерности, т.к. любое выражение гарантированно валидное. Это отличная новость, т.к. нам не нужно реализовывать вопросы размерности на уровне БД — а это и меньше работы, и потенциальный прирост производительности, т.к. нужно будет исполнять меньше логики в момент SQL запроса.
• Выражения нужно записывать в БД в своем первозданном (немодифицированном) виде. Этот принцип полезен практически для любой задачи. В нашем конкретном случае важно записывать первозданное выражение на тот случай, если таблица декомпозиции изменится.
• Получается, что БД только ответственна за расчет абсолютного значения. На практике ожидается, что эта функция будет использоваться для ORDER BY либо WHERE частей SQL запроса.

Внутренняя реализация

В этом месте проведем жирную черту. Мы закончили обсуждать интерфейс высокого уровня, который предоставляет наш калькулятор и начинаем двигаться вглубь (дебри) его реализации.

Интерфейс вектора размерности

Тут довольно тривиальная реализация – просто некоторый словарь, где ключом являются базовые размерности, а значение – это степень размерности. Векторное сложение и вычитание реализуются несколькими строчками на любом языке программирования.

Функцию isEqual(Dimension $dimension1, Dimension $dimension2) : bool можно реализовать следующим образом:

1. Вычтем одну размерность из другой.
2. Если полученный вектор состоит исключительно из нулей, значит размерности одинаковые.

Интерфейс выражения

В интерфейс выражения нам еще нужно добавить один “внутренний” метод, который нам облегчит жизнь при реализации метода formatQuantity(). Метод под названием containsDimensionlessMember() будет возвращать bool и указывать на то, может ли это выражение каким-то образом мутироваться, чтобы численно равняться какой-то величине. Т.к. на численное значение влияет лишь константа, поэтому метод так и называется “имеешьЛиТыБезразмерныйЧлен”.

Этот интерфейс будет иметь 2 реализации: под единицу измерения и под константу. Так будет очень удобно – единица измерения диктует размерность и по надобности ее можно/нужно декомпозировать, тогда как константа заведомо безразмерна и только влияет на абсолютное значение результата.

Я здесь просто приведу листинг кода на PHP. Думаю, так будет проще, чем писать словами.

Константа

  /**
   * Determine physical dimension of this mathematical expression.
   *
   * @return array
   *   Dimension array of this mathematical expression
   */
  public function dimension() {
    // Мы безразмерный член в любом выражении.
    return array();
  }

  /**
   * Test whether this mathematical expression includes a dimensionless member.
   *
   * Whether this mathematical expression contains at least 1 dimensionless
   * member.
   *
   * @return bool
   *   Whether this mathematical expression contains at least 1 dimensionless
   *   member
   */
  public function containsDimensionlessMember() {
    return TRUE;
  }

  /**
   * Format a certain amount of quantity within this mathematical expression.
   *
   * @param float $quantity
   *   Quantity to be formatted
   *
   * @return MathematicalExpression
   *   Formatted quantity into this mathematical expression. Sometimes the
   *   mathematical expression itself must mutate in order to format the
   *   quantity. So the returned mathematical expression may not necessarily be
   *   the mathematical expression on which this method was invoked. For
   *   example, the expression "unit" would mutate into "1 * unit" in order to
   *   have a dimensionless member and therefore be able to format the $quantity
   */
  public function formatQuantity($quantity) {
    // Когда нам говорят сверху “Ты должен равняться столько-то”,
    // то мы просто перезаписываем свое значение.
    $this->constant = $quantity;
    return $this;
  }

  /**
   * Numerically evaluate this mathematical expression.
   *
   * @return float
   *   Numerical value of this mathematical expression
   */
  public function evaluate() {
    // Численно мы равны самому себе.
    return $this->constant;
  }

  /**
   * Decompose (simplify) this mathematical expression.
   *
   * @return MathematicalExpression
   *   Decomposed (simplified) version of this mathematical expression
   */
  public function decompose() {
    // Дальше разлагаться некуда, поэтому возвращаем самого себя.
    return $this;
  }

Единица измерений

Для упрощения статьи, давайте оставим за ее рамками вопросы работы со справочной таблицей декомпозиции (той таблицей, где мы храним данные о том, как небазовые единицы измерений можно разложить на базовые). Просто представьте, что в нашем классе “единицы измерений” уже есть свойство, и в него записано декомпозиция. Если же это базовая единица, то это свойство не проинициализировано.

  /**
   * Determine physical dimension of this mathematical expression.
   *
   * @return array
   *   Dimension array of this mathematical expression
   */
  public function dimension() {
    // Если мы комплексная единица, то делегируем размерность в нашу декомпозицию.
    // В противном случае мы базовая единица размерности, о чем мы гордо заявляем
    // в возвращаемом векторе размерности.
    return is_object($this->decomposition) ? $this->decompose()->dimension() : array($this->identifier() => 1);
  }

  /**
   * Test whether this mathematical expression includes a dimensionless member.
   *
   * Whether this mathematical expression contains at least 1 dimensionless
   * member.
   *
   * @return bool
   *   Whether this mathematical expression contains at least 1 dimensionless
   *   member
   */
  public function containsDimensionlessMember() {
     // По определению, мы единица измерений, а следовательно, не являемся
     // безразмерным членом.
    return FALSE;
  }

  /**
   * Format a certain amount of quantity within this mathematical expression.
   *
   * @param float $quantity
   *   Quantity to be formatted
   *
   * @return MathematicalExpression
   *   Formatted quantity into this mathematical expression. Sometimes the
   *   mathematical expression itself must mutate in order to format the
   *   quantity. So the returned mathematical expression may not necessarily be
   *   the mathematical expression on which this method was invoked. For
   *   example, the expression "unit" would mutate into "1 * unit" in order to
   *   have a dimensionless member and therefore be able to format the $quantity
   */
  public function formatQuantity($quantity) {
    // Если от нас просят численно равняться чему-то, мы поступаем хитро.
    // Ведь мы – единица измерений, математика – это не наша прерогатива.
    // Поэтому мы на лету создаем выражение, где умножаем сами себя на единицу.
    // В таком выражении уже есть константа, в которую можно вписать $quantity.
    // Дальше мы просто делегируем вызов в это выражение, которое мы собрали 
    // “на лету”.

    // We expand this unit into "1 * $this" so we get a dimensionless
    // member that can be formatted.
    return (new MathematicalExpression(1 * “ . $this->toString()))->formatQuantity($quantity);
  }

  /**
   * Numerically evaluate this mathematical expression.
   *
   * @return float
   *   Numerical value of this mathematical expression
   */
  public function evaluate() {
    // Если мы уже являемся базовой единицей измерения, то
    // для нас не существует понятия абсолютной величины.
    // Какая абсолютная величина метра? - Заметьте, я сказал “метра”,
    // а не “одного метра”.
    return is_object($this->decomposition) ? $this->decompose()->evaluate() : NULL;
  }

  /**
   * Decompose (simplify) this mathematical expression.
   *
   * @return MathematicalExpression
   *   Decomposed (simplified) version of this mathematical expression
   */
  public function decompose() {
    // Если мы сложенная единица измерений, то делегируем.
    if (is_object($this->decomposition)) {
      return $this->decomposition->decompose();
    }
    // Иначе разлагаться дальше некуда и мы возвращаем сами себя.
    return $this;
  }

Математическая операция

Здесь реализация будет немного сложнее.

Во-первых, давайте обусловимся записывать константы и единицы измерений через знак умножения, т.е. 10 meter на самом деле надо бы записывать в виде 10 * meter. Это очень полезно, т.к. позволяет писать только единицы измерений meter / second так и их комбинации любой сложности: 10 * meter / second или 10 * meter / (2 * second).

В основу мы возьмем бинарное дерево. В ноде дерева будет оператор, а двумя детьми его операнды. Такой конструкцией мы можем строить выражения любой сложности. Выражение 10 * meter + 20 * inch будет выглядеть вот так:

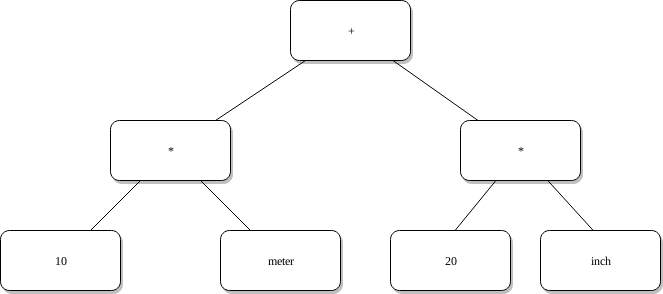
Заметьте, в листьях такого дерева (терминальной ноде) будут либо единицы измерений либо константы, а в остальных нодах – операторы.

По большей части реализация оператора делегирует вызовы в правильном порядке своим двум операндам. Наши 4 оператора отличаются друг от друга только в считанных местах. Поэтому я написал один класс-реализацию и такие считанные места параметризировал через свойство $this->operator, в этом свойстве упакованы следующие параметры:

• Расчет абсолютного значения имея на руках абсолютные значения обоих операндов. Эту часть в реализации я абстрагировал в $this->operator['evaluate callback'].
• Необходимость сравнения размерности – некоторые операторы требуют, чтобы оба их операнда обладали идентичной размерностью (сумма), а другие не выставляют такого требования (умножение). Для этого мы храним простой булиновский флаг в $this->operator['dimension check'].
• Расчет результирующей размерности при известных размерностях обоих операндов – абстрагировано в $this->operator['dimension callback'].
• Самая сложная часть – это логика, отвечающая за форматирование какого-то абсолютного количества (метод formatQuantity()). Она абстрагирована в $this->operator['split quantity callback'], который должен распределить абсолютное значение между первым и вторым операндом так, чтобы хотя бы в одном из них была “красивая” константа.

  /**
   * Determine physical dimension of this mathematical expression.
   *
   * @return array
   *   Dimension array of this mathematical expression
   */
  public function dimension() {
    // Здесь ответ зависит от конкретного оператора.
    // В случае со сложением/вычитанием, размерность не изменится.
    // А вот в случае умножения/деления, изменения будут. Соответственно,
    // нужно делегировать в колбек под каждый из операторов.
    // 
    // Отдельно предлагаю рассмотреть оператор возведения в степень.
    // При этом операторе результат зависит от абсолютного значения второго
    // операнда. Размерность “meter ^ 2” отличается от “meter ^ 3”. Поэтому мы
    // даем полный контекст в dimension callback – размерность и абсолютное 
    // значение обоих операндов, а не просто их размерность.

    $dimension_callback = $this->operator['dimension callback'];
    list($evaluate1, $evaluate2) = $this->evaluateOperands();
    return $dimension_callback($this->operand1->dimension(), $this->operand2->dimension(), $evaluate1, $evaluate2);
  }

  /**
   * Test whether this mathematical expression includes a dimensionless member.
   *
   * Whether this mathematical expression contains at least 1 dimensionless
   * member.
   *
   * @return bool
   *   Whether this mathematical expression contains at least 1 dimensionless
   *   member
   */
  public function containsDimensionlessMember() {
     // Внутри нас есть константа тогда, когда хотя бы у одного из наших
     // операндов есть константа.
    return $this->operand1->containsDimensionlessMember() || $this->operand2->containsDimensionlessMember();
  }

  /**
   * Format a certain amount of quantity within this mathematical expression.
   *
   * @param float $quantity
   *   Quantity to be formatted
   *
   * @return MathematicalExpression
   *   Formatted quantity into this mathematical expression. Sometimes the
   *   mathematical expression itself must mutate in order to format the
   *   quantity. So the returned mathematical expression may not necessarily be
   *   the mathematical expression on which this method was invoked. For
   *   example, the expression "unit" would mutate into "1 * unit" in order to
   *   have a dimensionless member and therefore be able to format the $quantity
   */
  public function formatQuantity($quantity) {
    $contains_dimensionless1 = $this->operand1->containsDimensionlessMember();
    $contains_dimensionless2 = $this->operand2->containsDimensionlessMember();
    list($quantity1, $quantity2) = $this->evaluateOperands();

    // Прежде всего, если константа есть только в одном из 2х операндов, то 
    // задача очень простая – делегировать вызов в тот операнд, который имеет
    // константу. К примеру: (“1 * meter”)->formatQuantity(100); при таком выражении
    // делегировать можно только в единичку, т.к. во 2м операнде (метр) некуда
    // “вписать” величину.
    if ($contains_dimensionless1 xor $contains_dimensionless2) {
      if ($contains_dimensionless1) {
        $this->operand1->formatQuantity($quantity / $quantity2);
      }
      else {
        $this->operand2->formatQuantity($quantity / $quantity1);
      }
    }
    else {
       // В этой ветке обрабатывается случай, когда оба операнда имеют константы.
       // К примеру “1 * foot + 1 * inch”. Тогда нужно выбрать такое соотношение 
       // между первым и вторым операндами, чтобы в первом операнде было какое-то       
       // “красивое” число, а остаток отдать второму операнду на форматирование.
       // Сама логика нахождения такого “красивого” соотношения зависит от 
       // конкретного оператора. Ближе к концу статьи я приведу примеры реализации
       // split quantity функций для некоторых операторов.
      $split_quantity = $this->operator['split quantity callback'];
      list($quantity1, $quantity2) = $split_quantity($quantity, $quantity1, $quantity2, $this->operator);

       // Имея на руках “красивое” количество на каждый из операторов, делегируем.
      $this->operand1->formatQuantity($quantity1);
      $this->operand2->formatQuantity($quantity2);
    }
    return $this;
  }

  /**
   * Numerically evaluate this mathematical expression.
   *
   * @return float
   *   Numerical value of this mathematical expression
   *
   * @throws UnitsMathematicalExpressionDimensionException
   *   Exception is thrown if this mathematical expression has inconsistency in
   *   physical dimensions
   */
  public function evaluate() {
    // Некоторые операторы требуют, чтобы размерности операндов совпадали.
    if ($this->operator['dimension check'] && !units_dimension_equal($this->operand1->dimension(), $this->operand2->dimension())) {
      throw new UnitsMathematicalExpressionDimensionException();
    }
    list($evaluate1, $evaluate2) = $this->evaluateOperands();

     // Имея на руках численное значение обоих операндов, мы делегируем
     // саму математику – там $evaluate1 и $evaluate2 будут сложены/вычтены
     // друг из друга, либо умножены/поделены в зависимости от того, какой
     // у нас оператор в $this->operator.
     $evaluate_callback = $this->operator[‘evaluate callback’];

    return $evaluate_callback($evaluate1, $evaluate2);
  }

  /**
   * Decompose (simplify) this mathematical expression.
   *
   * @return MathematicalExpression
   *   Decomposed (simplified) version of this mathematical expression
   */
  public function decompose() {
     // Банально делегируем декомпозицию на первый и второй операнды
     // и из результата собираем новую операцию с тем же самым оператором.
    return new OperatorMathematicalExpression($this->operator, $this->operand1()->decompose(), $this->operand2()->decompose());
  }

  /**
   * Retrieve operand #1 from this mathematical operator.
   *
   * @return MathematicalExpression
   *   Operand #1 from this mathematical expression
   */
  public function operand1() {
    return $this->operand1;
  }

  /**
   * Retrieve operand #2 from this mathematical operator.
   *
   * @return MathematicalExpression
   *   Operand #2 from this mathematical expression
   */
  public function operand2() {
    return $this->operand2;
  }

  /**
   * Numerically evaluate both operands and return them as an array.
   *
   * @return array
   *   Array of length 2: the 2 operands numerically evaluated
   */
  protected function evaluateOperands() {
    $evaluate1 = $this->operand1->evaluate();
    $evaluate2 = $this->operand2->evaluate();
     // На случай, если один из операндов – это единица измерений, 
     // мы подставляем такое абсолютное значение на место единицы
     // измерений, которое не повлияет на результат.
     // Для суммы, это будет 0. Для умножения – единица.
     // Это как х = х * 1 из математики 6го класса. Таким образом
     // мы добиваемся того, что единицы измерений (которые не
     // обладают математической природой) встраиваются в
     // математический контекст, не искажая его.
    if (is_null($evaluate1)) {
      $evaluate1 = $this->operator['transparent operand1'];
    }
    if (is_null($evaluate2)) {
      $evaluate2 = $this->operator['transparent operand2'];
    }
    return array($evaluate1, $evaluate2);
  }

Такая реализация отлично покрывает нужды суммы, вычитания, умножения и деления. В заключение приведу листинг некоторых колбеков.

Колбеки для суммы

function units_operator_add_evaluate($operand1, $operand2) {
  // Банально суммируем два количества.
  return $operand1 + $operand2;
}

function units_operator_add_dimension($dimension1, $dimension2, $operator1, $operator2) {
  // Т.к. для суммы размерность обоих операндов должна совпадать, то
  // достаточно просто вернуть одну из двух размерностей как результирующую.
  return $dimension1;
}

function units_operator_add_split_quantity($total_quantity, $quantity1, $quantity2, $operator) {
  // Логика для суммы следующая: для операнда, который включает наибольшую единицу
  // измерений (в случае футы + дюймы это будет футы), подобрать целое число. Остаток
  // отдать на форматирование в оператор, который включает меньшую единицу. Т.е. мы
  // подбираем красивое число для главной единицы и “все остальное” записываем во вторую
  // единицу измерений.
  $greatest_quantity = max($quantity1, $quantity2);
  $for_greater_quantity = floor($total_quantity / $greatest_quantity) * $greatest_quantity;
  $for_fewer_quantity = $total_quantity - $for_greater_quantity;
  return $quantity1 > $quantity2 ? array($for_greater_quantity, $for_fewer_quantity) : array($for_fewer_quantity, $for_greater_quantity);
}

Колбеки для умножения

function units_operator_multiply_evaluate($operand1, $operand2) {
  return $operand1 * $operand2;
}

function units_operator_multiply_dimension($dimension1, $dimension2, $operator1, $operator2) {
  // При умножении размерности складываются.
  return units_dimension_add($dimension1, $dimension2);
}

function units_operator_multiply_split_quantity($total_quantity, $quantity1, $quantity2, $operator) {
  // На практике умножение используется в formatQuantity() методе только на самом
  // последнем шаге, когда умножается константа на единицу измерений:
  // 1 * foot + 1 * inch. Вот эти 1 * foot и 1 * inch умножения, о которых я говорю.
  // Поэтому я вставил довольно простую заглушку в этот колбек – отдаем все
  // количество в первый операнд, который на практике всегда оказывается
  // константой.
  return array($total_quantity, $operator['transparent operand2']);
}

Похожим образом выглядят колбеки для остальных операций.

Задания со звездочкой*

В школе в самом конце урока в учебнике были задания со звездочкой – на пятерку с плюсом. В этот раздел я поместил как раз такие дополнительные задания, реализацию которых уже не буду включать в статью.

База данных

Мы проговорили, что БД должна уметь численно просчитывать значение выражений, чтобы их можно было сортировать и фильтровать (покажи список учеников, отсортированных по росту или покажи учеников, выше 3 фута + 5 дюймов). Я пробовал разные способы реализации этой задачи на инструментарии SQL и в конечном итоге пришел к recursive CTE (recursive Common Table Expressions).

Человекоудобный интерфейс

Надо бы реализовать конвертацию наших выражений в строку, удобную для восприятия человеком (такая нотация называется инфиксной). В интерфейс выражения можно добавить метод toInfix(). Но нужна еще и обратная операция – нечто, что сможет распарсить инфиксное выражение в наше бинарное дерево. Эта задача решается довольно тривиально при наличии Википедии и здравомыслящего мозга. Почитайте о парсинге инфиксной и постфиксной нотации. Наличие такого инфиксного парсера значительно облегчает жизнь программисту, т.к. выражения можно собирать простым вызовом units_mathematical_expression_create_from_infix(“10 * meter * kilogram / second”). А не громоздкой конструкцией в несколько строк, где под каждый операнд мы создаем собственный объект и вкладываем один объект в другой для построение конечного бинарного дерева.

Дополнительные операции

Математика не ограничивается только четырьмя операциями. Еще есть степень, корень, факториал. В моей реализации помимо четырех, рассмотренных здесь, так же есть степень.
Более того, некоторые операторы имеют лишь 1 операнд: факториал, к примеру. Значит, мою модель еще можно и нужно делать гибче, если мы хотим поддерживать большее количество операций.

Нелинейные конвертации

И вот задача прям с двумя звездочками**! Вся модель, которую я описал, работает лишь при линейных конвертациях, т.е. при таких единицах измерений, которые конвертируются между собой за счет умножения на какой-либо коэффициент.

Такая схема конвертации очень практична, а потому и очень популярна: в метре 100 сантиметров, в футе – 12 дюймов. Но есть одна загвоздка, и имя той загвоздки градусы Фаренгейта. Честно, затрудняюсь представить как кто-либо мог придумать такую шкалу температур… А потом кто-то мог ее взять как основную для измерения температуры. Но увы, факт давно минувших дней, и нам, потомкам тех мужей, не остается ничего иного, как адаптироваться под ситуацию.

Проблема с Фаренгейтом следующая. Цитата из Википедии:

На шкале Фаренгейта температура таяния льда равна +32 °F, а температура кипения воды — +212 °F (при нормальном атмосферном давлении). При этом один градус Фаренгейта равен 1/180 разности этих температур.

Возможно, из этого определения это не так очевидно, но Фаренгейт не конвертируется линейно в Цельсий. Нет такого коэффициента, умножив на который, мы сконвертируем одно в другое.

А теперь магия, следите внимательно за руками: возьмем 100 метров. Представим их в виде километров: 0.1 км. Умножим оба варианта на 10. Получим 1000 метров и 1 км. Приведем оба варианта к метрам и увидим ожидаемый результат – оба выражения равны между собой.

Повторим трюк с температурой: возьмем 10 C. Представим в виде фаренгейта (50 F). Умножим на 10. Получим 100 C и 500 F. Сконвертируем оба в цельсий: 100 C и 260 C. Каково? Выполняя вроде бы одну и ту же операцию двумя разными способами мы получили очень разные ответы. Это значит, что Цельсий и Фаренгейт используют принципиально отличные шкалы и никакая математика между ними не применима! По крайней мере без какой-либо адаптации этой математики ну или не все 100% этой математики.

Попытайтесь проанализировать что же можно сделать с этой проблемой.

Заключение

Позволю себе последний абзац для того, чтобы обернуться назад и посмотреть на описанное мной решение с точки зрения архитектуры. Вам задача в самом начале показалось сложной? Предложенная архитектура проста к пониманию? Вы заметили, что для ее решения я использовал 3 интерфейса, 3 объекта и под дюжину функций?

Удобно ли расширить такой калькулятор на дополнительные базовые единицы измерений (допустим, валюта: доллары, евро) – запросто! Даже код править не нужно. Можно ли добавить новые математические операции – можно, путем локальных правок в заведомо определенные места.

Удобно ли пользоваться таким калькулятором? Хорошо ли с портативностью (переиспользованием) такой системы? — Вроде бы неплохо, ее можно использовать на чисто программном API уровне, можно прикрутить какой-нибудь юзер интерфейс с кнопочками. Переписать реализацию на другой язык программирования тоже не подразумевает особой сложности.

Архитектура не перегружена абстракциями, каждый актер делает одну точную самодостаточную операцию – это значит, что случайно “не понять” смысл какой-то операции и использовать ее не по назначению затруднительно. Все функции/методы в своей реализации не занимают больше 20 строк кода. Поставить это все на юнит-тестирование банально просто. Архитектуры на подобие этой я и называю элегантными. Они красивы и лаконичны.

Автор: bucefal91

Источник