Обычная аналогия для объяснения градиентного спуска такая: человек застрял в горах во время сильного тумана и должен спуститься вниз. Самый логичный способ — осмотреть поверхность вокруг и медленно проложить путь, следуя вниз по склону.
Такова суть градиентного спуска, но аналогия всегда разваливается, когда мы переходим в многомерное пространство, фактическая геометрия которого нам мало известна. Хотя обычно это не становится проблемой, потому что градиентный спуск, кажется, работает вполне нормально.
Но вот важный вопрос: насколько хорошо градиентный спуск выполняется на реальной Земле?
Определение весов и функции стоимости
В общей модели градиентный спуск подбирает веса для модели, которая минимизирует функцию стоимости. Это обычно некоторое представление ошибок, сделанных моделью по ряду прогнозов. Но здесь мы ничего не предсказываем, следовательно, у нас нет «ошибок», поэтому адаптация к путешествию по земле требует немного расширить контекст обычного машинного обучения.
В нашем алгоритме земного путешествия цель — выйти на уровень моря с любой начальной позиции. То есть мы определим «веса» как широту и долготу, а «функцию стоимости» как текущую высоту над уровнем моря. Иными словами, градиентный спуск должен оптимизировать значения широты и долготы таким образом, чтобы минимизировать высоту над уровня моря. К сожалению, у нас нет математической функции для всей земной поверхности, поэтому рассчитаем значения стоимости по растровому набору данных по высотам от NASA:
import rasterio
# Open the elevation dataset
src = rasterio.open(sys.argv[1])
band = src.read(1)
# Fetch the elevation
def get_elevation(lat, lon):
vals = src.index(lon, lat)
return band[vals]
# Calculate our 'cost function'
def compute_cost(theta):
lat, lon = theta[0], theta[1]
J = get_elevation(lat, lon)
return JГрадиентный спуск учитывает градиент функции стоимости по отношению к каждой переменной, для которой выполняется оптимизация. Он настраивает переменные так, чтобы они уменьшали функцию затрат. Это легко, если ваша функция стоимости — математическая метрика типа средней квадратичной ошибки. Но как мы уже упоминали, наша «функция стоимости» — это поиск в базе данных, поэтому не от чего взять производную.

К счастью, можно аппроксимировать градиент так же, как путешественник в нашей аналогии: оглядываясь вокруг. Градиент эквивалентен наклону, поэтому оценим наклон, взяв точку немного выше текущего местоположения и точку немного ниже его (в каждом измерении) — и разделим их, чтобы получить оценочную производную. Такой вариант должен работать достаточно хорошо:
def gradient_descent(theta, alpha, gamma, num_iters):
J_history = np.zeros(shape=(num_iters, 3))
velocity = [ 0, 0 ]
for i in range(num_iters):
cost = compute_cost(theta)
# Fetch elevations at offsets in each dimension
elev1 = get_elevation(theta[0] + 0.001, theta[1])
elev2 = get_elevation(theta[0] - 0.001, theta[1])
elev3 = get_elevation(theta[0], theta[1] + 0.001)
elev4 = get_elevation(theta[0], theta[1] - 0.001)
J_history[i] = [ cost, theta[0], theta[1] ]
if cost <= 0: return theta, J_history
# Calculate slope
lat_slope = elev1 / elev2 - 1
lon_slope = elev3 / elev4 - 1
# Update variables
theta[0][0] = theta[0][0] - lat_slope
theta[1][0] = theta[1][0] - lon_slope
return theta, J_historyОтлично! Заметьте, что эта функция отличается от большинства реализаций градиентного спуска тем, что в неё не передаются переменные X или Y. Наша функция стоимости не требует вычисления ошибки каких-либо прогнозов, поэтому нам нужны только переменные, которые мы тут оптимизируем. Давай запустим её на горе Олимп в Вашингтоне:
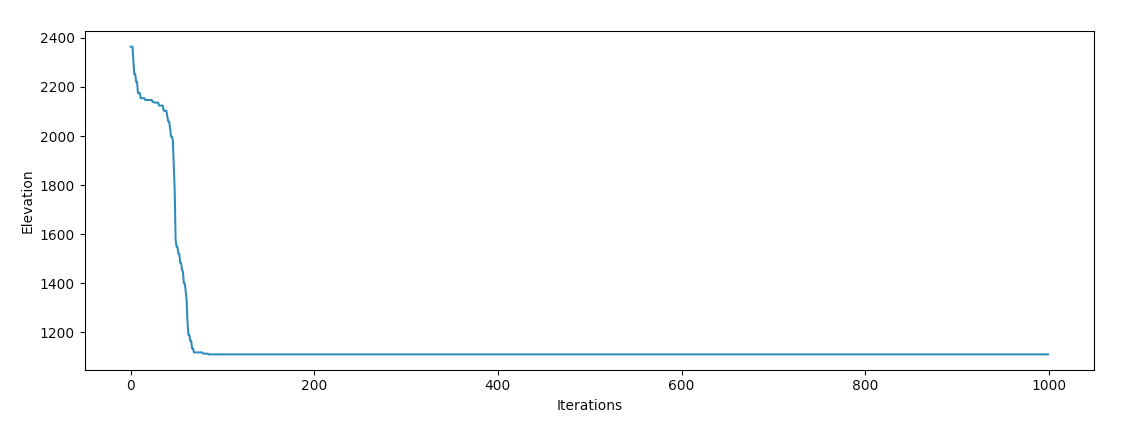
Хм, похоже, он застрял! То же самое происходит при тестировании в большинстве других мест. Оказывается, наша Земля переполнена локальными минимумами, и градиентный спуск испытывает огромные трудности с поиском глобального минимума, если запускается из локальной области даже рядом с океаном.
Оптимизация с инерцией
Стандартный градиентный спуск — не единственный инструмент, поэтому попробуем оптимизацию с инерцией (momentum optimization). Инерция основана на реальной физике, так что её применение к градиентному спуску на реальной геометрии — привлекательная идея. К сожалению, если разместить на вершине Олимпа даже очень большой валун и отпустить, то вряд ли у него хватит инерции докатиться до океана, поэтому придётся использовать здесь некоторые нереалистичные (в физическом смысле) значения gamma:
def gradient_descent(theta, alpha, gamma, num_iters):
J_history = np.zeros(shape=(num_iters, 3))
velocity = [ 0, 0 ]
for i in range(num_iters):
cost = compute_cost(theta)
# Fetch elevations at offsets in each dimension
elev1 = get_elevation(theta[0] + 0.001, theta[1])
elev2 = get_elevation(theta[0] - 0.001, theta[1])
elev3 = get_elevation(theta[0], theta[1] + 0.001)
elev4 = get_elevation(theta[0], theta[1] - 0.001)
J_history[i] = [ cost, theta[0], theta[1] ]
if cost <= 0: return theta, J_history
# Calculate slope
lat_slope = elev1 / elev2 - 1
lon_slope = elev3 / elev4 - 1
# Calculate update with momentum
velocity[0] = gamma * velocity[0] + alpha * lat_slope
velocity[1] = gamma * velocity[1] + alpha * lon_slope
# Update variables
theta[0][0] = theta[0][0] - velocity[0]
theta[1][0] = theta[1][0] - velocity[1]
return theta, J_historyПосле некоторой настройки переменных у градиентного спуска должны увеличиться шансы найти океан:
Успех! Интересно наблюдать за поведением оптимизатора. Кажется, он попал в долину и «перекатывался» с одной на другую сторону во время спуска, что согласуется с нашей интуицией, как должен себя вести в реальном мире объект с чрезвычайно высокой инерцией.
Заключительные мысли
В реальности Земля должна быть очень лёгкой функцией для оптимизации. Поскольку она в основном покрыта океанами, более двух третей возможных входных значений для этой функции возвращают оптимальное значение функции стоимости. Но наша планета страдает от локальных минимумов и невыпуклой географии.
Думаю, из-за этого она предоставляет много интересных возможностей для изучения того, как методы оптимизации машинного обучения работают на осязаемых и понятных локальных геометриях. Похоже, на Олимпе они неплохо справились, так что будем считать обычную аналогию для объяснения градиентного спуска «подтверждённой»!
Если у вас есть мысли по этому поводу, дайте знать в твиттере!
Код проекта здесь.
Автор: m1rko





