Небольшое предисловие
Меня всегда интересовала история появлений научных понятий. Перед изучающим новый предмет сначала встает череда безликих определений. Некоторые из них таковыми и остаются, другие привлекают внимание и со временем вырастают в полноценные объекты «картины мира». В качестве недоступного идеала такого стремления можно привести высказывание Литлвуда о Рамануджане:
каждое натуральное число было его лучшим другом
Мне всегда было интересно не только освоить понятие, но и разобраться, как оно появилось. За каждым определением всегда стоит личность. Интересно понять, какие идеи лежали в основе того или иного понятия и почему новые определения были восприняты и поддержаны другими людьми с таким энтузиазмом, что остались в учебниках.
Далее будет приведено небольшое исследование подобного рода, объектом которого является понятие регулярного выражения.
Нейронные сети МакКаллока-Питса
Как это не удивительно, но основной мотивацией для введения понятия регулярного выражения послужили нейронные сети. Немного об истории осознания этого понятия.
Понятие нейронной сети появилось в результате междисциплинарного взаимодействия. В 1942 году Уолтер Питтс — американский логик, работавший, в основном, в области когнитивной психологии, познакомился с известным физиологом Уорреном МакКаллоком. МакКаллок приехал в Чикаго для работы в местном Университете. У Питтса не было жилья и МакКаллок предложил пожить у него. Следствием зародившихся отношений стала работа «Логическое исчисление идей, относящихся к нервной деятельности».
В работе была предложена модель нервной деятельности человека. Эта модель была основана на абстракции понятия нейрона. Математический объект, полученный в результате такой абстракции, называют нейроном МакКаллока-Питса. Нейрон МакКаллока-Питтса представляет собой формальную модель нервной клетки, состоящей из тела и нескольких отростков, называемых нервными волокнами. В модели МакКаллока-Питтса клетка — это ячейка, снабженная специальным числовым атрибутом, так называемым порогом. Из каждого нейрона выходит ребро, моделирующее нервное волокно и называемое аксоном. Аксон может разветвляться, но обязательно является входом для одного или нескольких других нейронов. Таким образом, кроме исходящего волокна (аксона) нейрон имеет несколько входящих волокон (синапсов).
Некоторые из входов могут быть возбуждающими, другие — тормозящими. Возбуждающие волокна обозначаются обычной стрелкой, а тормозящие — прерывистой стрелкой. Каждый нейрон генерирует сигнал на аксоне только в том случае, если количество возбуждающих входных сигналов превышает порог данного нейрона. Аксоны обозначаются сплошными исходящими стрелками. Тело нейрона обозначается треугольником. Таким образом, нейрон МакКаллока-Питтса можно изобразить следующим образом:
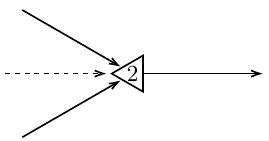
Нейроны объединяются в сети, называемые нейронными сетями МакКаллока-Питтса. Вся сеть функционирует как конечный автомат. Для этого в сети вводится понятие времени. В каждый момент времени выходной сигнал от некоторого нейрона переходит на вход того нейрона, к которому этот нейрон подключен в качестве входа. Таким образом, фиксируя моменты времени, мы получаем состояния нервной сети, а переход из одного состояния в другое происходит при увеличении текущего момента времени.
Аксоны некоторых нейронов в сети могут быть синапсами для этих же нейронов, т.е. нейроны могут образовывать «петли». Наличие петель очень важно для нейронной сети МакКаллока-Питтса. Петли позволяют запоминать сигналы, которые были поданы на вход. Если на вход нейрона был подан сигнал, то можно возбудить аксон, который является входом для этого же нейрона, и, таким образом, с этого момента данный нейрон будет находиться в активном состоянии, самовозбуждаясь с каждым новым моментом времени.
Рассмотрим, например, нейронную сеть МакКаллока-Питтса, которая является простейшим запоминающим устройством. Собственно, запоминающим устройством будет один нейрон с петлей, остальные элементы сети представляют собой «обслуживающие» элементы.
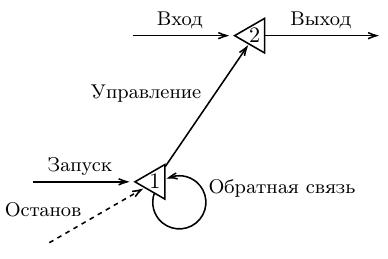
Возбуждение некоторого сигнала на выходе сети будем называть событием. Возникает вопрос: можно ли по данному событию определить его предысторию, т.е. последовательность прохождения сигналов по сети в предыдущие моменты времени так, чтобы дойти до входов в данную сеть? Если принять во внимание, что сети МакКаллока-Питтса были придуманы для моделирования деятельности , то этот вопрос можно переформулировать так: какие внешние факторы привели к тому состоянию ума, в котором в данный ситуации он находится? Оказывается, наличие петель не дает возможности точно определить, когда произошло данное событие, а наличие альтернатив (входов от двух различных нейронов в данный нейрон) не позволяет определить точно, где это событие произошло. МакКаллок и Питтс считали, что именно это ограничение является основой психологического феномена под названием «абстракция».
Регулярные события
Американский математик Стивен Клини изучал события в сетях МакКаллока-Питтса. В работе «Представление событий в нервных сетях и конечных автоматах» Клини предложил изящный способ описания таких событий с помощью языка регулярных выражений. Можно сказать, что всякая сеть МакКаллока-Питтса представима в виде регулярного выражения, описывающего входы этой сети и предыстории входных сигналов, которые привели к тому, что возбудился один из выходных сигналов.
Напомним, что событием в сети МакКаллока-Питтса называется появление сигнала на ее выходе, т.е. на аксоне, который не является синапсом ни для какого нейрона данной сети. Клини изучал вопрос: возбуждение каких входов (т.е. синапсов каких-то нейронов сети, которые не являются аксонами никаких нейронов данной сети) в сеть привело к тому, что на данном выходе появился сигнал? Рассмотрим в качестве примера, сеть, изображенную на рисунке ниже:
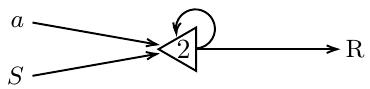
Предположим, что на вход синапса, обозначенного символом a, подается сигнал. Единственный нейрон данной сети имеет порог 2, поэтому аксон этого нейрона будет возбужден только в том случае, если будет активен синапс начала S. В этом случае аксон R активен, но также активно его ответвление, снова входящее в нейрон. Что мы можем сказать в момент времени t о том, какова предыстория появления сигнала R на выходе? Оказывается, только то, что в момент времени t-1 точно был активен аксон a. Также можно предположить, что в момент времени t-2 и ранее аксон a также мог быть возбужден. Мы не можем точно сказать, было ли это в действительности, а если и было, то в какой момент времени аксон a стал активным. Поэтому нашу гипотезу мы выражаем посредством a*. Таким образом, предысторию появления события R можно описать выражением a*a. Очевидно, везде, где в сети встречаются петли, мы не сможем точно сказать о времени появления возбуждающего сигнала на входе.
Существуют также неточности другого рода. Рассмотрим следующую сеть:
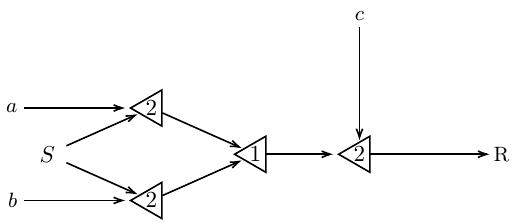
Здесь выходной синапс R возбуждается, если активны аксоны c и синапс предыдущего нейрона. Что мы можем сказать о том, когда будет возбужден этот синапс? Оказывается, только то, что один из аксонов a или b возбужден. Этот факт мы обозначаем посредством выражения a|b. Таким образом, предысторию возникновения события R можно описать как (a|b)c.
В рассмотренных примерах мы получили удобный способ описания событий в сетях МакКаллока-Питтса. Для описания используются три оператора: *, | и оператор конкатенации (присоединения). Оказывается, с помощью этих трех операторов можно описать события в любой сети МакКаллока-Питтса. Событий, которые не описывались бы подобным образом, в сетях МакКаллока-Питтса не существует. Это предмет доказательства т.н. теоремы Клини. События, которые могут быть описаны посредством указанных выше операторов, Клини назвал регулярными (в том смысле, что других событий не имеется). Регулярные события можно описывать выражениями, используя для этого операторы *, | и конкатенации. Такие выражения получили название регулярных выражений. Учитывая, что каждая сеть МакКаллока-Питтса представляет собой конечный автомат, мы получили удобный способ описания автоматных языков с помощью регулярных выражений.
Забытое возвращается
Работа Клини вышла в середине 50-х годов двадцатого века. Как часто случается с научными понятиями, не находящими себе применения, работа была забыта. Так продолжалось бы и до сих пор, но в конце 60-х годов американский программист Кен Томпсон обнаружил, что регулярные выражения удобно использовать для задания шаблонов поиска строк в длинных текстах. Регулярное выражение преобразуется в конечный автомат, которые производит поиск строк, соответствующих шаблонам. Для построения конечного автомата Томпсон придумал специальный алгоритм, который сейчас носит название «построение Томпсона». Томпсон включил механизм поиска по регулярным выражениям в разрабатываемый им текстовый редактор ed и с тех пор регулярные выражения стали de facto стандартом для задания поисковых шаблонов.
История понятия регулярного выражения дает хорошую возможность увидеть, как эволюционируют объекты человеческой мысли, путешествуя от одних областей человеческой деятельности к другим. Эти области могут быть очень далеки друг от друга, и обмен понятиями между этими областями часто выглядит неожиданно. Интересно, что глубокая работа Клини, в которой были введены регулярные выражения, не сделало это понятие известным. Но, по сути, простое утилитарное применение понятия, возвело регулярные выражения на пик славы.
Автор: mefrill






