Здравствуйте, уважаемые читатели!
В процессе разработки приложения под Android, которое предполагает взаимодействие пользователя с графическими примитивами (точками, линиями, эллипсами, прямоугольниками и т.д.), возникла довольно неприятная ситуация: пользователь может задать произвольный многоугольник и сделать его неактивным, однако чтобы в будущем была возможность активировать данный многоугольник и продолжить с ним работь (например, переместить в другое место или добавить/удалить вершины) необходимо для неактивного объекта определить, коснулся ли пользователь данного объекта, т.е. потребовалось решить вопрос о принадлежности точки многоугольнику.
Данная задача широко известна в вычислительной геометрии, однако в русскоязычной литературе практически не описана. Чтобы исправить данное недоразумение предлагаю вашему вниманию результаты моего исследования данной темы.
Введение
В вычислительной геометрии обычно предполагается, что многоугольник простой, т.е. без самопересечений, но проблему рассматривают и для многоугольников сложной формы. Данная задача наиболее часто решается следующими методами:
- методом учёта числа пересечений, который подсчитывает сколько раз луч, выходящий из точки P, пересекает границы многоугольника. Если число пересечений нечётно, то объявляется, что точка лежит внутри многоугольника, если чётно – снаружи.
- методом учёта числа оборотов, который подсчитывает число оборотов, которое делает ориентированная граница многоугольника вокруг данной точки P. В алгебраической топологии это число называется winding number. Точка считается лежащей снаружи многоугольника только в случае, если число оборотов равно нулю, в противном случае точка лежит внутри контура многоугольника.
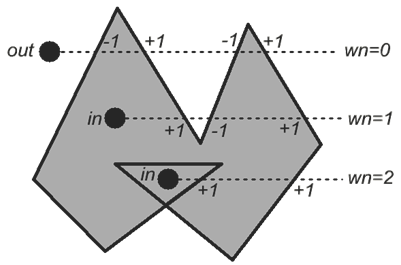
Если многоугольник простой (т.е. не имеет самопересечений), то оба метода дают одинаковый результат для всех точек. Однако если многоугольник имеет сложную форму, то методы могут возвращать разные результаты для некоторых точек. Например, если многоугольник пересекается с собой, тогда при использовании метода учёта пересечений точки в регионе пересечения определяются как точки снаружи. Однако те же самые точки будут считаться лежащими внутри многоугольника при использовании метода учёта числа оборотов (см. рисунок).
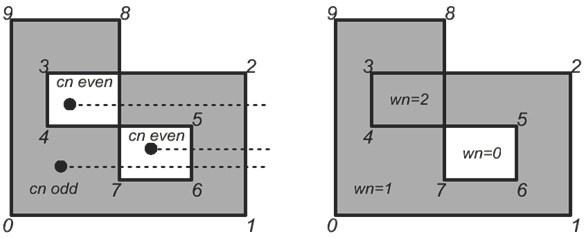
Метод учёта числа пересечений и его оптимизация подробно описаны в данной статье, поэтому давайте рассмотрим второй алгоритм решения задачи.
Метод учёта числа оборотов
Данный метод точно определяет, лежит ли точка внутри сложного многоугольника, сравнивая, как много раз полигон оборачивается вокруг точки. Точка не принадлежит полигону только в том случае, когда число оборотов (winding number) равно нулю.
Пусть непрерывная двумерная кривая C определяется точками C(u) = C(x(u), y(u)), где 0 ≤ u ≤ 1 и C(0) = C(1). Также пусть P – точка, не лежащая на кривой C. Объявим вектор c(P, u) (от точки P до кривой C):
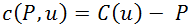
и единичный вектор w(P, u):
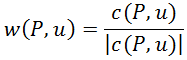 ,
,
который даёт непрерывную функцию W(P): C → S1, отображая точку C(u) кривой C к точке w(P, u) на единичной окружности S1 = {(x, y) | x2 + y2 = 1}. Это отображение может быть представлено в полярных координатах:
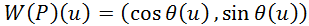 ,
,
где θ(u) – положительный поворот против часовой стрелки в радианах.
Тогда число оборотов wn(P, C) непрерывной кривой C вокруг точки P равно целому числу раз, когда W(P) поворачивает кривую C вокруг единичной окружности S1. Это соответствует гомотопическому классу S1 и может быть вычислено через интеграл:
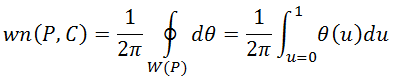
Когда кривая C является полигоном с вершинами V0, V1, …, Vn = V0, интеграл сокращается до знаковой суммы углов, под которыми каждое ребро многоугольника ViVi+1 противолежит к точке P. Таким образом, если θi равно углу между PVi и PVi+1, тогда:
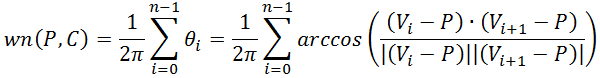 (1)
(1)
На рисунке показано, как графически можно представить знаковую сумму углов.
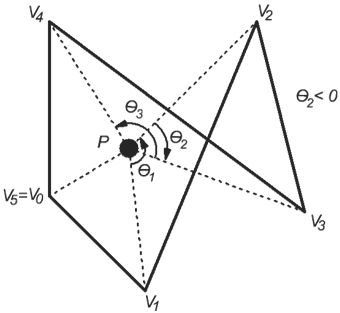
Очевидно, что формула (1) не очень эффективна, поскольку использует требовательную к вычислительным мощностям тригонометрическую функцию арккосинуса. Необходимо заменить эту формулу более эффективной.
Оптимизация метода учёта оборотов
Возьмём любую точку Q на единичной окружности. Тогда, как кривая W(P) оборачивается вокруг S1, она проходит точку Q определённое количество раз. Если считать (+1), когда кривая проходит Q против часовой стрелки, и (-1), когда кривая проходит по часовой стрелке, то накопленная сумма будет общим количество раз, сколько W(P) оборачивается вокруг S1 и равна wn(P, C) – числу оборотов непрерывной кривой C вокруг точки P. Далее, если мы возьмём бесконечный луч R с началом в точке P и проходящей в направлении вектора Q, то пересечение луча R и кривой C соответствует точке, где W(P) проходит Q. Для разработки математического аппарата необходимо различать положительные и отрицательные переходы, где C пересекает R в направлениях справа налево или слева направо. Это можно определить по знаку скалярного произведения вектора нормали к C и направление вектора q = Q, и необходимо вычислить скалярное произведение для каждого ребра полигона. Для горизонтального луча R c началом в точке P, достаточно проверки, находится ли конец ребра выше или ниже луча. Если ребро пересекает прямой луч снизу вверх, то пересечение положительно (+1), но если он пересекает ребро сверху вниз, то пересечение отрицательно (-1). Сумма знаков пересечений даёт число оборотов wn(P, C).
Более того, можно избежать вычисления фактической точки пересечения ребра и луча. Для этого достаточно определить, с какой стороны ребро пересекается лучом. Если восходящее ребро пересекает луч справа от точки P, то P находится левее ребра, т.к. треугольник ViVi+1P ориентирован против часовой стрелки. Если нисходящее ребро пересекает луч слева, то точка P находится правее ребра, поскольку треугольник ViVi+1 ориентирован по часовой стрелке.
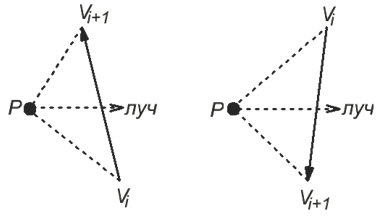
На рисунке слева изображено восходящее ребро, а справа — нисходящее.
В заключение хотелось бы сказать, что метод учёта оборотов требует полного перебора вершин заданного многоугольника и в этом, на мой взгляд, заключается его недостаток. Однако, он с лихвой компенсируется легкостью реализации и наличием всего двух операций умножения на каждой итерации цикла перебора вершин.
Основной источник: GeometryAlgorithms.com
Автор: dmitryustimov





