Автоматное программирование. Часть 3. Диаграмма состояний и переходов. Продолжение

В предыдущей статье речь шла о психологических аспектах описания динамических процессов при помощи диаграммы состояний и переходов (то есть в автоматном стиле) и о том, что диаграмма состояний и переходов даёт лучшее понимание динамического процесса. Сегодня я продолжу рассмотрение диаграммы состояний, олицетворяющей автоматный подход, и способы её воплощения в код. Тема предыдущей статьи органично перетекает в сегодняшний материал, поэтому я рекомендую ознакомится с ней.

Оглавление.

Диаграмма состояний != граф-схема.

Как уже было сказано, диаграмма состояний это альтернативная, более удобная форма записи программных алгоритмов. Более того, диаграмма состояний это естественная форма записи динамического процесса, в то время как алгоритмическая граф-схема это искусственная конструкция, которая уже содержит в себе особенности реализации, которые бывают очевидны и не требуют того, чтобы их указывали отдельно, либо вообще ухудшают понимание, хотя технически верно описывают последовательность требуемых действий.
Но диаграмма состояний это не просто другая графическая нотация записи граф-схемы, она обладает некоторыми отличными особенностями. На рис 1 (б, в) приведены диаграммы состояний одного и того же автомата, соответствующего исходной граф-схеме статье рис. 1 (а).

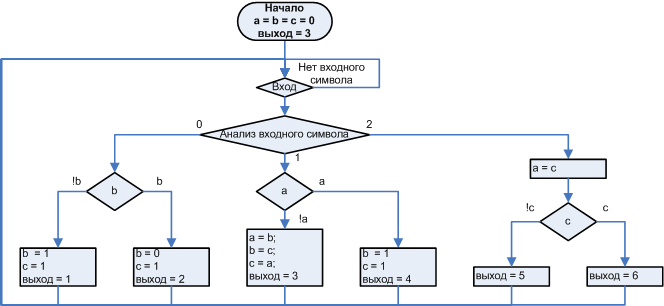
Рисунок 1 а). Исходная граф-схема

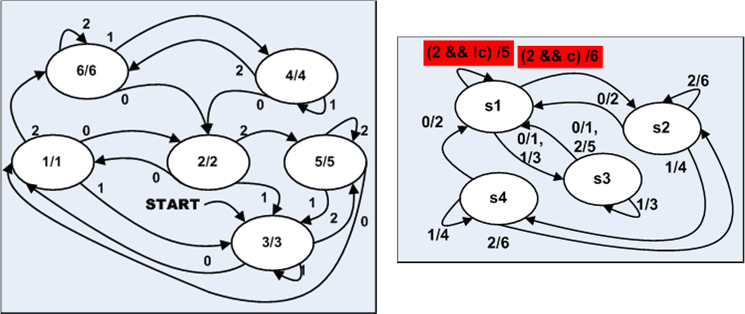
Рисунок 1 б), в). Диаграммы состояний эквивалентных автоматов, реализующих алгоритм
(а).

На рис 1 (в) приведён пример некорректной записи диаграммы состояний и переходов. Некорректность в том, что переходы выделенные красным прямоугольником определяются не только входными событиями, но и дополнительно флагом с, который для этого состояния соответствует одноимённому флагу исходной граф-схемы рис. 1 (а), из-за чего уже нельзя отслеживать состояние процесса, рассматривая только входные символы, нужно каким-то образом учитывать логику изменения флага c. Проблема даже не в самом флаге с, а в том, что логика изменения этого флага не привязана к одному только состоянию s1. Если бы события связанные с изменением этого флага были бы связаны только с s1, такой проблемы не было бы. Выделенные красным цветом переходы зависят от того, каким путём попали в s1, что противоречит определению автомата, согласно которому реакция зависит только от входного символа и текущего состояния. Назовём это принцип автоматности, чтобы ссылаться на него дальше по тексту.

Граф-схему ярко выраженной неавтоматной реализации алгоритма рис. 1 (а) не так просто записать в виде корректной диаграммы состояний, поскольку явно не определены состояния, и соответственно не определены переходы между ними. Для составления диаграммы рис. 1 (б) по алгоритму рис. 1 (а) потребовалось получить эквивалентный автомат. Методика получения эквивалентных автоматов для любой граф-схемы станет предметом рассмотрения в одной из следующих статей, сейчас ограничусь констатацией, что это принципиально можно сделать, потому что любое цифровое устройство, в том числе и любая «неавтоматная» программа, это цифровой автомат, который обладает состояниями в математическом смысле, несмотря на то, что эти состояния явно не описаны. Такие состояния подобны квантовым фотонам в квантовой электродинамике, их можно упрощённо описать: они везде и нигде конкретно, но они существуют и действуют.

В этом примере, в силу случайности, каждая ветвь граф-схемы соответствует одному состоянию. Другими словами, каждый выходной символ получается только в одном состоянии. Однако, будь логика изменения флагов иной, оказалось бы, что один выходной символ получается в нескольких разных состояниях, или если сказать иначе — одна и та же ветвь граф-схемы соответствует нескольким разным состояниям. Это ещё более сложный с точки зрения понимаемости случай.

Поскольку речь зашла о состояниях, возникает совершенно естественный вопрос: «с каким количеством состояний придётся иметь дело?». При автоматной реализации количество состояний мы задаём в известной мере произвольно, исходя из потребностей.

В случае неавтоматного подхода, количество потенциальных состояний эквивалентного автомата составляет величину до:

$$display$$2^text{суммарная_разрядность_всех_переменных_определяющих_поведение, бит. }$$display$$

То есть добавление даже одной переменной определяющей поведение, типа bool удвоит количество «структурных», условно назову их «схемотехнических возможных» состояний. Многие из этих состояний — недостижимые состояния. Все недостижимые состояния исключаются автоматически, специально подобранной логикой действий над переменными определяющими поведение и предполагается, что эти действия, налагаясь одно на другое, дадут требуемый результат. С точки зрения психологии, напомню, это динамический процесс как последовательность разнонаправленных действий дающих в итоге требуемый результат. Как было сказано ранее, очень сложная форма для понимания. Неплохой аналогией отличия между автоматным описанием (диаграмма состояний) и алгоритмическим описанием (граф схема) динамического процесса может быть исследование вместо графика функции графика её производной.

В случае, когда переменных определяющих поведение немного, сложность алгоритмического описания не столь заметна, но с ростом количества таких переменных сложность восприятия алгоритма растёт экспоненциально, и угнетающе действует на психику.

Следует пояснить термин Переменная определяющая поведение. В случае неавтоматной реализации это фактически любая переменная, создающая ветвление алгоритма. В случае автоматной реализации это переменная Внутреннее состояние. В качестве переменной Внутреннее состояние может быть переменная типа перечисление, где перечислены все состояния(=просто int), или даже просто переменная типа bool если всего два состояния. Далее я продемонстрирую разные варианты программных реализаций автоматов.

Как уже было сказано в начале статьи, граф-схема это не только форма записи автомата, но и форма записи обычного алгоритма. То, что операция условного перехода изображается стрелкой перехода, думаю, не вызывает удивления, но как изобразить цикл? Допустим наш автомат перебирает прямоугольную таблицу, то есть общее число комбинаций переменных вертикального и горизонтального циклов составит m * n. значит ли что у результирующего автомата будет столько же состояний, или иными словами как записать в автоматном стиле цикл? Рассмотрим цикл:

for(i = 5; i--; ){}

C точки зрения условия этого цикла значения счётчика 5,4,3,2,1 – одно и то же значение. Да, внутри тела цикла i это параметр, поведение программы отличается при разных значениях этого параметра, но с точки зрения режима работы цикла for, переменная-счётчик может принимать два значения 0 и не 0. Переменная i это так сказать псевдофлаговая переменная.
Возвращаясь к автомату обхода таблицы, отмечу, что этот автомат имеет два состояния и две псевдофлаговые переменные:

• счётчик горизонтального цикла, определяет состояние:
  {0} – Вертикальный цикл,
  {1,…,5,…} – Горизонтальный цикл,
• счётчик вертикального цикла определяет условие окончания работы.

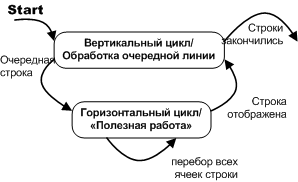
Рисунок 2. Запись вложенных циклов при помощи диаграммы состояний.

Автомат Out_text из примера в «Введении» показанный на рис. 3 представляет интерес с точки зрения событий, вызывающих изменение состояния автомата.

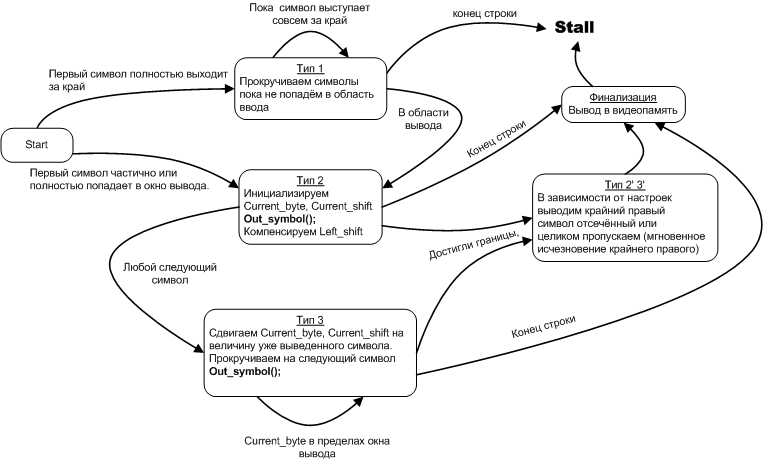
Рисунок 3. «Автомат отображения текстовых блоков», диаграмма состояний.

Единственное событие, которое можно рассматривать как внешнее, — конец строки, все остальные события этого автомата сугубо внутренние, они порождаются работой самого алгоритма. Однако это не нарушает принцип автоматности, рассмотренный выше, потому что все события влияющие на переход из некоторого состояния, порождаются самим этим же состоянием, то есть поведение автомата не зависит от того каким путём мы попали в это состояние.

Автоматно реализованную программу можно изобразить в виде граф-схемы, и она останется автоматно реализованной. На рис. 4. приведён пример граф-схемы соответствующей диаграмме состояний и переходов приведённой в начале статьи

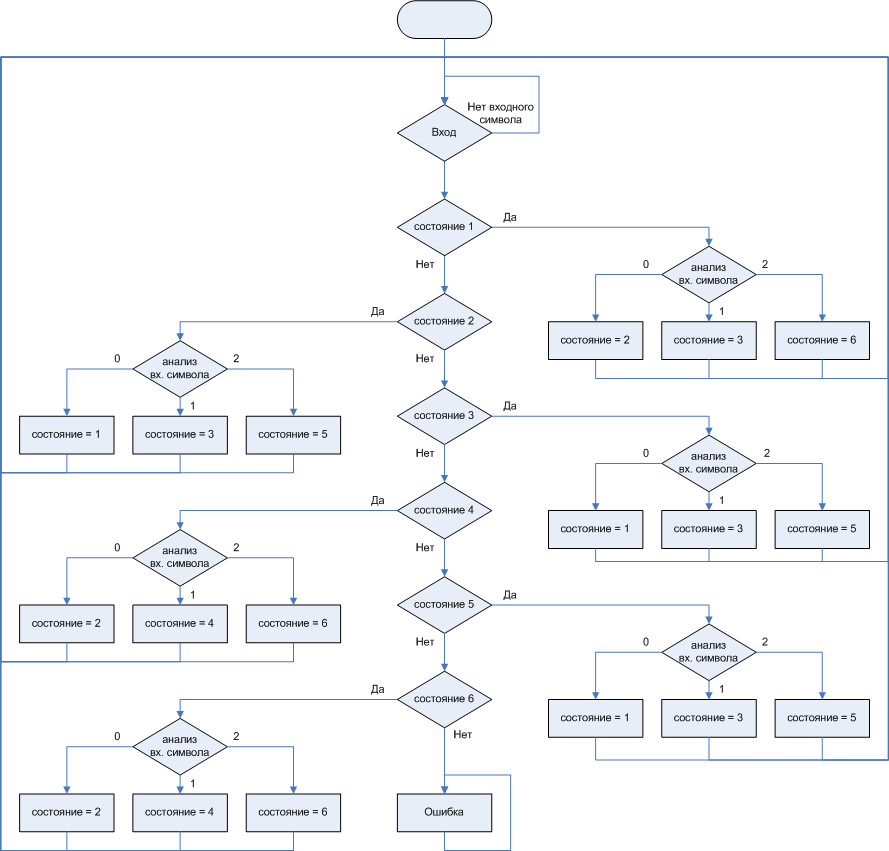
Рисунок 4. Граф-схема, соответствующая автомату, описываемому рис. 1 (б)

Как видно, при записи автоматно-реализованных программ, граф-схема заметно проигрывает диаграмме состояний в отношении компактности.
Теперь рассмотрим, что отличает автоматное программирование от автоматной схемотехники.

Артефакты автоматной схемотехники.

Чтобы лучше понимать о чём идёт речь, введём две категории программных автоматов – символьные и функциональные. Символьные автоматы это автоматы, принимающие последовательность символов на входе, и выдающие последовательность символов на выходе. Это полный аналог классических абстрактных автоматов, автоматов которые собственно и рассматривает дискретная математика. Символьные автоматы используются для распознавания кодов, разбора регулярных выражений, лингвистического анализа, а так же для оптимизации функциональных автоматов, и алгоритмов в целом. Мы затронем способы их реализации далее в сегодняшней статье, и подробно обсудим в одной из следующих статей.
Этим автоматам противопоставляются функциональные программные автоматы, (буду их называть в тексте программаты) — полный аналог прикладных и управляющих программ компьютера или микроконтроллера. Это те же самые модули, подпрограммы, которые управляют периферией микроконтроллера, или выполняют какую-либо полезную работу, или реализуют интерактивную работу с пользователем, но они спроектированы и реализованы автоматно.
В автоматной схемотехнике следующим этапом после разработки абстрактного автомата является структурный синтез, когда абстрактные сигналы и состояния кодируются «живыми» битами, выбираются способы кодирования, строится логическая схема, работающая с уже закодированными битами. Функциональные программные автоматы это программный аналог структурных автоматов.

Если рассматривать функциональные автоматы исключительно с позиций схемотехники, и не видеть в них ничего большего чем структурные автоматы, то такой узкий взгляд скорее мешает. Такой подход, являющийся калькой с автоматной схемотехники даёт шаблон того, как должен быть устроен автоматно спроектированный модуль.

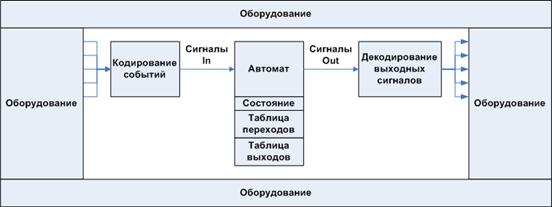
Рисунок 5. Общепринятый шаблон реализаций программных автоматов

Это приводит к тому, что процесс проектирования становится громоздким, включающим в себя не нужные в большинстве случаев формальные шаги, предписываемые этим шаблоном.
Но не превращение реально происходящих процессов в набор формализованных сигналов или использование некоторого «автоматного» API даёт преимущество автоматному программированию. Преимущество даёт запись динамического процесса в категориях диаграммы состояний, это делает программирование более предсказуемым. Грамотное разбиение автомата на операционный и управляющий автоматы, и как часть этого разбиения -правильный, разумный выбор операционного автомата, вот что делает решение эффективным, и в следующей статье будет это будет убедительно показано.

Механическое копирование поведения разработчика схемотехнических автоматов, вот что я имел ввиду под словом артефакты, от которых автоматное программирование избавляется, покидая колыбель автоматной схемотехники, мы ведь имеем дело с программой. Программа чрезвычайно удобный и пластичный материал, и именно пластичность этого материала сделала его столь популярным. Программируя обычным способом, мы избавлены от рутины проектирования цифровых схем. Когда нам нужно выполнить действие, мы проверяем условие и выполняем его, и не требуется писать специальную функцию-триггер. О чём я? Можно написать так:

if(IO_latch->Data_1_received && IO_latch->Permission)
{
  State = 5;
}

а можно и так

typedef bool paTrigger();
typedef void paAction();

struct tLink_Trigger_Action
{

  paTrigger * Trigger;
  paAction * Action;
  int Next_state;

};

bool Trigger_X(){return(IO_latch->Data_1_received && IO_latch->Permission);};

void Action_X(){State = 5;};


tLink_Trigger_Transition Table[States_max][ Triggers_max] = {
/*State_0*/{},
/*State_1*/{ …,{ Trigger_X, Action_X }, … },
/*State_2*/{},
/*State_3*/{},
/*State_4*/{}};

uint Engine (uint Message)
{
  if(State->Trigger())
  {
    State->Action();
    State = State->Next_state;
  }
…
}

, чувствуете разницу?

Единственное что могут возразить сторонники сверхформализма – при обычном программировании меньше учёта, при автоматносхемотехническом способе все биты сосчитаны. На это я отвечу, что если возникает проблема с учётом какого-то параметра, стоит создать подавтомат, который будет заниматься учётом, и освободить основной автомат от рутины. Это совет по практической декомпозиции.

Драматизм ситуации, связанной с программатами, в том то и состоит, что автоматный ментальный шаблон, давая удобный инструмент моделирования и анализа динамических процессов, одновременно тяжёлой дланью доминирует над разработчиками, лишая их простых радостей обычного программирования. Это на мой взгляд одна из самых серьёзных причин того, что технология автоматного программирования не может подняться выше чем экзотическая диковинка.

Как несложно догадаться, естественный путь преодоления этой противоречивой ситуации — взять лучшее от обеих парадигм. В этом случае внутреннее состояние становится не столько указанием как обрабатывать следующее входящее событие, но оно становятся неким режимом работы. Это важно. Состояние скорей следует рассматривать как подпрограмму, в которой алгоритм находится некоторое время. При этом он может обрабатывать входные сигналы, транслировать их в выходные, никуда не переходя. Подразумевается, что в одном состоянии программат выполняет однотипную работу, всё что выходит за рамки однотипности переносится в другое состояние. Переход из состояния в состояние производится не любым сигналом, а только значимыми для этого алгоритма событиями. И эти события мы выбираем сами, исходя из выбранных нами же состояний. И соответственно, каждое состояние-режим может содержать вложенные программаты.

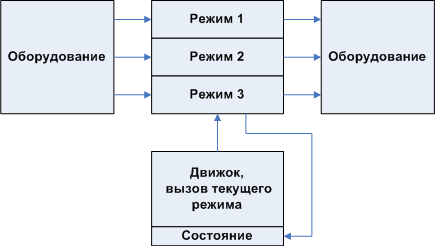
Рисунок 6. Конструктивный шаблон, при котором состояние это режим работы.

Но программат не находится монопольно в функции-режиме до тех пока не совершит переход. Он выполняет короткие итерации, в ходе которых контролирует обстановку. При этом приложение в целом выглядит как:

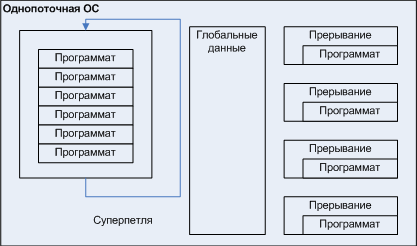
Рисунок 7. Сообщество программатов.

То есть используя программаты, мы приходим к концепции корпоративной многозадачности, только в отличии от классических алгоритмов корпоративной многозадачности, когда обычное с виду приложение само в какой-то момент обращается с какой-либо целью к ОС и таким образом возвращает управление системе, программаты изначально проектируются как программы, которые получают управление только на один шаг, выполняют его и передают управление обратно, до следующей итерации. Отличие корпоративной многозадачности и программатов формально условное, но сам автоматный взгляд на программы подразумевает их итерационный характер, поэтому не возникает таких проблем, что программат «забывает» передавать управление обратно.

Программаты могут без проблем работать и под управлением многопоточных ОС, как это показано на рис. При этом, конечно, их корпоративная многозадачность оказывается вроде как и не нужна, однако само автоматное устройство модуля сохраняет все рассмотренные выше плюсы, связанные с автоматным проектированием.

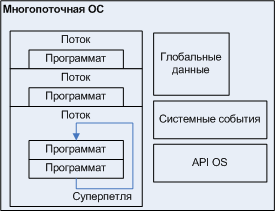
Рисунок 8. Программаты в многопоточной среде.

Поскольку программат может выполнять однократные действия, происходящие при совершении перехода, а может совершать протяжённую деятельность, находясь в одном и том же состоянии — режиме работы, то его диаграмма состояний приобретает черты и автоматов Мили и автоматов Мура. Например автомат парковочный счётчик, описывается диаграммой состояний.

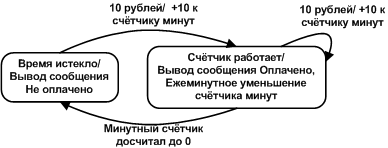
Рисунок 9. Программат «Парковочный счётчик», описание совмещает черты автоматов Мили и Мура.

Пример парковочного счётчика ещё не рассматривался, однако глядя на диаграмму состояний без труда можно понять, о чём идёт речь. Обратите внимание, описание этого счётчика диаграммой состояний гораздо информативней, чем было бы описание этого же автомата сделанное при помощи текста.

С точки зрения теории, я не совершаю ошибки, объединяя в одной диаграмме состояний черты автоматов Мили и автоматов Мура. Когда нужно будет осуществить математические операции над таким автоматом, он может рассматриваться как автомат Мили. Для абстрактных автоматов, при том же функционале автомат Мили может получиться с меньшим числом состояний. Существуют математические методики преобразования автоматов Мили в автоматы Мура и наоборот.

Описанное проливает немного света на то, чем являются программаты, перейдём к способам их реализации.

Способы реализации функциональных программных автоматов.

Начнём с граф-схемы рассматривавшейся ранее, для удобства показанной на рис. 10.

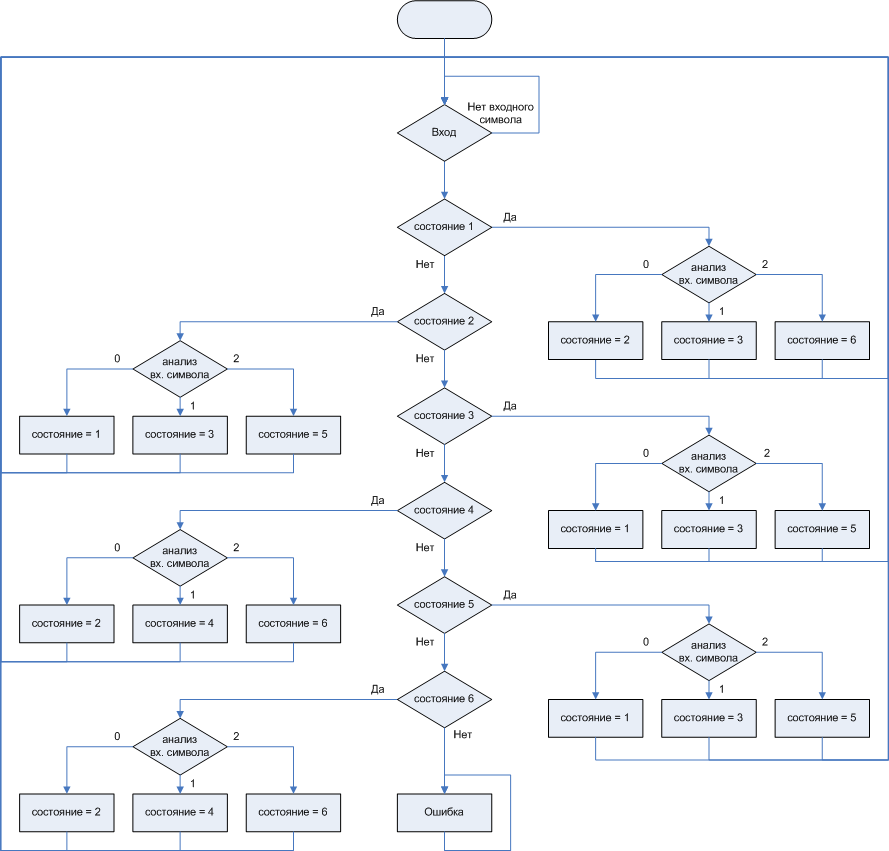
Рисунок 10. Граф-схема, которую требуется реализовать.

Самое очевидное, вытекающее напрямую из граф-схемы решение «в лоб», – использовать для определения состояния конструкцию множественной альтернативы языка Си, оператор switch. При получении очередного входного символа программа определяет текущее состояние, и для каждого состояния проводится анализ входного символа, при этом для каждого входного символа задан не только переход в определённое состояние, но и выходной символ.

#define mStep ((uword) (-2))// см. далее

uint Automaton (uint Input)
{

  static uint State = 3;
  uint Out;
  
  {действия, которые выполняются и без переходов, если требуются };   
  
  switch (State)
  {
    
  ////////////////////////////////////////////  
  case 1:
    
    switch (Input)
    {    
    /////////// 
    case 0:      
      {дополнительные действия, если требуются };   
      State = 2;  
      Out = 2;
      break;      
    /////////// 
    case 1:
      {дополнительные действия, если требуются };   
      State = 3;
      Out = 3;      
      break;      
    /////////// 
    case 2:     
      {дополнительные действия, если требуются };   
      State = 6;
      Out = 6;      
      break;    
    /////////// 
    case mStep:
      break;    
    }
    
    break;
    
  ////////////////////////////////////////////  
  case 2:
    ...
  ////////////////////////////////////////////  
  case 3:
    ...
  ////////////////////////////////////////////  
  case 4:
    ...
  ////////////////////////////////////////////  
  case 5:
    ...
  ////////////////////////////////////////////  
  case 6:
    ...
  default:
   // Error
    
  };

  return(Out);

}

Подобными способами реализованы автоматы в Switch-технология и в IAR visualState.

Поскольку концепция состояний программата трактует их как режимы работы программы, в которых та может некоторое время функционировать, не совершая переходов, но в то же время продолжая свою «мелкую деятельность», то должен быть входной символ, который гарантированно не переводит программат в новое состояние (если только он не перейдёт сам, по внутренним причинам), однако активирует его каждую итерацию. Символ шаг – mStep.

Второй вариант реализации, принципиально отличающийся: сделать обработчик каждого события, как это показано на листинге

uint Message_i0_handler(uint &State)
{

  uint Out;

  switch (State)
  {
    
  ////////////////////////////////////////////  
  case 1:
    {дополнительные действия, если требуются };   
    State = 2;
    Out = 2;      
    break;   
  ////////////////////////////////////////////  
  case 2:
    {дополнительные действия, если требуются };   
    State = 1;
    Out = 1;      
    break;    

  ... 

  };

  return(Out);


}

uint Message_i1_handler(uint &State)
{
  ...
}

uint Message_i2_handler(uint &State)
{
  ...
}

void Message_Step_handler(uint &State)
{

    switch (State)
  {
    
  ////////////////////////////////////////////  
  case 1: 
    {действия, которые выполняются и без переходов, если требуются };   
    break;     
  ////////////////////////////////////////////  
  case 2: 
    {действия, которые выполняются и без переходов, если требуются };   
    break;      
  ////////////////////////////////////////////  
  case 3: 
    {действия, которые выполняются и без переходов, если требуются };   
    break;  

  };

  return(mStep);

}



typedef uint (*paMessage_handler)(uint &State);

paMessage_handler Reactions[3] = { Message_i0_handler_for_s1, Message_i1_handler_for_s1, Message_i2_handler_for_s1};



uint Automaton (uint Input)
{

  Reactions [Input];

}

Рассмотренные выше варианты – базовые варианты, отражающие основные идеи, но они довольно громоздки и медлительны. Однако, они модифицируются безо всяких проблем в сторону уменьшения громоздкости (относительного) и ускорения работы (реального).
Модифицируем код, приведённый на листинге Вариант 2. Разобьём каждый обработчик событий Message_ixx_handler на набор функций, соответствующих каждому состоянию

uint Message_i0_handler_for_s1(uint &State)
{

    {дополнительные действия, если требуются };   
    State = 2;
    Out = 2;      

  return(Out);

}

uint Message_i0_handler_for_s2(uint &State)
{

    {дополнительные действия, если требуются };   
    State = 1;
    Out = 1;      

  return(Out);

}
...

uint Message_Step_handler_for_s1(uint &State)
{
  {действия, которые выполняются и без переходов, если требуются };   
  return(mStep);

}

typedef uint (*paMessage_handler)(uint &State);

paMessage_handler Reactions[6][3] = {

{ Message_i0_handler_for_s1, Message_i1_handler_for_s1, Message_i2_handler_for_s1},
...
{ Message_i0_handler_for_s6, Message_i1_handler_for_s6, Message_i2_handler_for_s6},


};

paMessage_handler Reactions_for_Step [6] = { Message_mStep_handler_for_s1, ..., Message_mStep_handler_for_s6 };


uint Engine(uint Input = mStep)
{

  uint State = 3;
 
  if(Input == mStep)
    
    return(Reactions_for_Step [State] (State));

  else

    return(Reactions[State][Input] (State));

}

При таком варианте хорошо реализуется схема диспетчеризции событий в обработчиках прерываний и их обработки из единого движка.
Схожий способ лежит в основе реализации шаблона boost.statechart.

Основной недостаток предыдущих двух вариантов: они артефакты автоматной схемотехники, то есть программируя таким образом, невозможно сохранить «программистский стиль» программирования, приходится использовать табличный стиль программирования, чрезмерно раздутый.

Рассмотрим что даёт табличный стиль программирования:

• "+" перечислены реакции на все события для каждого из состояний (для необрабатываемых событий стоят заглушки), т.е. имеется полнота описания.
• "-" Но при этом всё настолько громоздко реализуется, что велика суммарная вероятность какой-нибудь опечатки, или оставить не там заглушку. То есть о повышении надёжности речь не идёт, это притом, что автоматное программирование позиционирует себя как более надёжную методику разработки.

Немудрено, что компания IAR пошла по пути графического программирования автоматов visualState, посчитав что текстовый автоматносхемотехнический стиль программирования не для людей.

Гораздо более благодатным в плане возможностей для модификации оказывается вариант приведённый на листинге Вариант 1, если его расширить принятой концепцией состояний-режимов работы.

Пусть обработчик входных сигналов для каждого состояния (внешний switch) вынесен в отдельную функцию (функция-режим).

uint State_1 (uint &State, uint Input)
{

  {действия, которые выполняются и без переходов, если требуются };   

  switch (Input)
  {    
  /////////// 
  case 0:      
    {дополнительные действия, если требуется };   
    State = 2;  
    Out = 2;
    break;      
  /////////// 
  case 1:
    {дополнительные действия, если требуется };   
    State = 3;
    Out = 3;      
    break;      
  /////////// 
  case 2:     
    {дополнительные действия, если требуется };   
    State = 6;
    Out = 6;      
    break;        
  /////////// 
  case mStep:  
    // Ничего не делаем       
};

uint State_2 (uint &State, uint Input){...};

typedef uint (*paState)(uint &State, uint Input);

paState States[6] = {

{ State_1, ..., State_6},

};

uint Engine(uint Input = mStep)
{

  static uint State = 3;
 
  return(States [State] (State, Input));

}

При кажущемся сходстве с вариантом 3, этот больше соответствует концепции программата, как набора сменяющихся режимов. Каждая функция-состояние это функция-режим, которая сама опрашивает всю требуемую ей периферию, или засинхронизованный кадр данных из периферии, и совершает переходы на основании этого, а не только на основании символа Input.

Символ Input при этом может содержать однотипные для всех программатов системные сообщения. Это означает в частности, что сама функция-состояние может быть написана традиционным, максимально привычным способом.

Этот вариант показывает более высокое быстродействие по сравнению с вариантом 1, в силу того, что каждое значение переменной Внутреннее состояние однозначно сопоставлено с функцией, которая обрабатывает это состояние, и вызов функции-состояния сводится к тому, чтобы по индексу получить ячейку таблицы, которая содержит указатель нужной функции. В то же время, при реализации варианта 1, переменная Внутреннее состояние многократно сравнивается со значениями, которые соответствуют номерам-названиям состояний.

Хотя этот вариант более скоростной, количество рутины не сокращается. Главный минус этой реализации в том, что нужно иметь и таблицу состояний, и вести параллельный учёт состояний в заголовочнике и в файле кода, причём не copy/paste, так сказать проблема двойного описания. Однако и эта проблема решается довольно просто. Модифицируем указанный пример. Вместо переменной Внутреннее состояние, которая есть индекс указателя в константной таблице, можно использовать переменную Внутреннее состояние, которая сама и является указателем на функцию-состояние:

typedef uint (*paState)( void * argState, uint Input);

uint State_1 (paState * State, uint Input)
{

  {действия, которые выполняются и без переходов, если требуются };   

  switch (Input)
  {    
  /////////// 
  case 0:      
    {дополнительные действия, если требуется };   
    State = (paState*) State_2;  
    Out = 2;
    break;      
  /////////// 
  case 1:
    {дополнительные действия, если требуется };   
    State = (paState*) State_3;  
    Out = 3;      
    break;      
  /////////// 
  case 2:     
    {дополнительные действия, если требуется };   
    State = (paState*) State_6;  
    Out = 6;      
    break;        
  /////////// 
  case mStep:  
    // Ничего не делаем       


};
uint State_2 (paState *State, uint Input){...};

uint Engine(uint Input = mStep)
{

  static paState *State = (paState*) State_3;
 
  return(State(State, Input));

}

Описанный вариант уже почти не отличается от «естественного» программирования. Это становится ещё очевидней, если представить, что внутри конструкций switch и даже вместо них можно использовать конструкции типа

if(IO_latch->Data_1_received && IO_latch->Permission)
{
  State = 5;
}

От «естественного» программирования этот вариант отличается только тем, что отдельные состояния-режимы вынесены в отдельные функции. Однако, разбиение задачи на простые подзадачи-функции это один из основных приёмов любого программирования. Здесь же речь идёт только о том, что есть конструктивный критерий разбиения программы (отдельное состояние — отдельная функция), позволяющий избежать механистического, наивного дробления исходного кода: эта функция получилась большая, разделим её, например, по диагонали. Я утрирую, но когда нет критерия разбиения, оно будет либо скатываться в крайности (любой чих — отдельная функция), либо будет производиться на основе некоторого внутреннего чувства правильности происходящего, которое тренируется годами и даже тут автоматный способ представления процессов отличная помощь воображению, посколько удачно «структурирует поток сознания» в процессе разработки.

Ярким примером «естественного», но автоматного программирования является автомат tDisplay::Out_text, из «Введения». Этот автомат описывается диаграммой состояний и переходов.

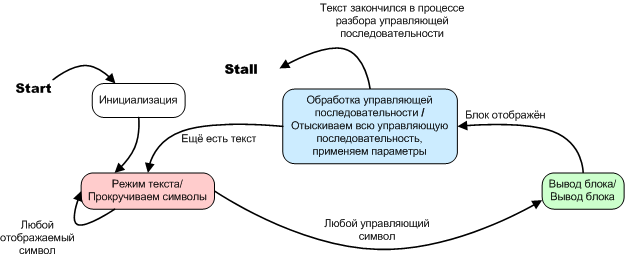
Рисунок 11. Диаграмма состояний и переходов автомата разбиения текста на блоки

Вариант 6. Исходник автомата разбиения текста.

Как видно из этого примера, все состояния вполне можно реализовать в виде одной функции. В этом примере нет необходимости использовать оператор goto, но я добавил его к имеющимся классическими структурными конструкциями — ветвлениями и циклу. Это сама по себе ещё одна структурная конструкция программирования — переход в состояние автомата. Пару слов подробней об этой структурной конструкции.

В общем случае каждое состояние помечено меткой а переходы между состояниями выполняются при помощи структурной конструкции goto Имя_метки_состояния;

Состояние всегда начинается с метки, программа не может попасть внутрь состояния иначе как через его входную точку. Их даже можно заключить в скобки {}, и (!) могут быть вложенные состояния внутри одной функции. Но это уже чересчур. Так обеспечивается соблюдение принципа модульности, даже при работе внутри единственной функции, поэтому ничто не нарушает принципов надёжного программирования допуская использование операторов goto. Все переходы совершаются в полном соответствии с диаграммой состояний. Это позволяет вносить изменения без повышения сложности, всё как бы разложено по полочкам и ничего лишнего.

Единственный минус такого решения – когда автомат начинает свою работу, он будет находиться в нём до тех пор, пока не перейдёт в состояние Stall. Для Дисплея это даже приветствуется, но функциональные программаты в системах реализованных как сообщества автоматов рис 7, бывает, не имеют возможности работать подобным образом. В таком случае каждое состояние следует описывать отдельной функцией, как и в примере Вариант 6, но переход осуществляется макросом:

      

typedef uint (*paState)( void * argState, uint Input);

#define mGoto(argState,argOut){
State = (paState*)argState;
return(argOut);
}

#define mStall_code ( (uword)(-1) )
#define mStall(){
return(mStall_code);
}

//Должен периодически запускаться 
uint Engine(paState *State, uint Input = mStep)
{
  
  return(State(State, Input));

}

Этот несложный API позволяет управлять поведением автомата из функций-состояний этого же автомата.
Такие команды невозможно вызвать для какого–то автомата находясь вне этого автомата, потому что их выполнение заканчивает работу функции.

Использование описанной системы команд выполняется по схеме.

paState *Display_state; 

void tDisplay::Out_text (int arg_x0, int arg_y0,
                         int arg_x1, int arg_y1,
                         int arg_x_shift, int arg_y_shift,
                         unsigned char * argText,
                         TMemo * argDebug)
{

   // Инициализация
          Display_state = (paState*) state__Inside_text_block; 
 
   // Движок
          while(Engine (Display_state, 0) != mStall_code);

          return;
 

}//void tDisplay::Out_text (int arg_x0, int arg_y0,
  

  

////////////////////////////////////////////////////////////////////////////
       ////////////////////////////////////////////////////////////////////////////
       ////////////////////////////////////////////////////////////////////////////
uint state__Inside_text_block(paState * State, uint Input)
{
  
  if(Input == mForce_Out_text_block)

    mGoto(state__Out_text_block, 0);


  while(1)
  {

    switch(*Text_end)
    {

      case '':
      case 'n':
        mGoto(state__Out_text_block, 0);

    }

    Text_end++;

  }
  
}// uint state__Inside_text_block(paState * State, uint Input)

  


////////////////////////////////////////////////////////////////////////////
       ////////////////////////////////////////////////////////////////////////////
       ////////////////////////////////////////////////////////////////////////////
uint state__Out_text_block(paState * State, uint Input)
{

  if(Text != Text_end)
  {

    // Вложенный вызов операционного автомата.
    Out_text_block();

    // После выполнения Execute_script в Line_width фактическое количество выведенных пикселов
    x_rel += Line_width;

  }

  // Сброс буфера произведён
  Text = Text_end;
        
  mGoto(state__Control_processing, 0);


}// uint state__Out_text_block(paState * State, uint Input)



////////////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////////       ////////////////////////////////////////////////////////////////////////////
uint state__Control_processing(paState * State, uint Input)
{

  if(*Text_begin == 0)
  {

    mStall();

  }

         // Обработка esc последовательности

  mGoto(state__Control_processing, 0);

}

При таком варианте реализации движок автомата может запускаться не в теле функции а в отдельном потоке, так сказать «совершать шаги». В случае с дисплеем такая необходимость неочевидна, но представим, что после отображения каждого блока требуется время, чтобы новые данные обработались и после этого передавать следующую порцию. Автоматно это реализуется эффективно даже когда нет многозадачной среды. Этот пример даёт возможность представить сферу полезности автоматной реализации. В этом случае вызов Out_text заряжает процесс, движок которого периодически запускается фоновой суперпетле или в обработчике прерывания, если объём вычислений позволяет это сделать

Описанный простой API очень удобен и весьма функционален. С его помощью можно модифицировать пример 4, и он будет выглядеть следующим образом. Движок тот же что и для варианта 4.

uint State_1 (paState * State, uint Input)
{

  {действия, которые выполняются и без переходов, если требуются };   

  switch (Input)
  {    
  /////////// 
  case 0:      

    {дополнительные действия, если требуется };   
    mGoto(State_2,2);

  /////////// 
  case 1:

    {дополнительные действия, если требуется };   
    mGoto(State_3,3);


  /////////// 
  case 2:     

    {дополнительные действия, если требуется };   
    mGoto(State_6,6);

  /////////// 
  case mStep:  
    // Ничего не делаем.   

  return (0);

};

Этот API удобен в практическом применении, несмотря на простоту охватывает огромную часть потребностей автоматосоставления.

Такой вариант в дальнейшем называется базовая конструктивная реализация. Слово конструктивная означает, что этот способ реализации вытекает непосредственно из практического опыта, как наиболее приемлемая.
В части примеров переменная внутреннее состояние объявлена в теле функции-движка как static, но это условность. На самом деле автомат описывается классом, и эта переменная часть класса-описателя автомата. Условимся называть описатель состояния автомата и рабочие переменные этого автомата термином контекст автомата. Вопрос контекста автомата, того какой конкретно структурой описываются автоматы, имеет много нюансов. Этому вопросу будет посвящена отдельная статья.

Способы реализации символьных программных автоматов.

Напоследок рассмотрим способы реализации простых символьных автоматов. Как было сказано выше, они образуют отдельное семейство, их концепция серьёзно отличается от функциональных автоматов, они являются классическими абстрактными автоматами, и способы реализации двух семейств автоматов отличаются, хотя имеют общие черты. Пусть имеется автомат, на вход которого поступает последовательность символов a,b,c, и который выдаёт 1 в случае, когда обнаруживает указанную последовательность, и 0 во все остальных случаях.
Пусть искомая последовательность bacab. Диаграмма состояний этого автомата изображена на рис. 12

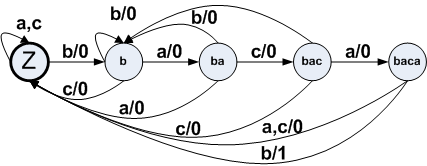
Рисунок 12. Автомат определения входной последовательности bacab.

В одной из следующих статей я покажу алгоритм автоматизированного составления таких автоматов, сейчас же рассмотрим, как максимально эффективно реализовать этот автомат. Проще всего составить двумерный массив

uint FSM[States_amount][Alphabet_size];

в котором каждый вложенный массив соответствует состоянию, а каждый элемент вложенного массива содержит индекс следующего состояния для каждого входного символа. Каждому входному символу, в общем случае сопоставляется индекс от 0 до Размер_алфавита – 1. Этот массив – классическая таблица переходов автомата. Поскольку выходной символ всегда 0, кроме единственного случая «код распознан», то таблицу выходов можно не создавать, но в случае, когда код распознан, в ячейке таблицы вместо следующего состояния, значения 0, 1,2, … будет стоять число 0xff..ff. В этом случае код возврата из движка 1, а индекс следующего состояния 0. Движок таких автоматов описывается простой функцией, без комментариев.

uint FSM[States_amount][Alphabet_size];

uint Engine(uint Input)
{

  static uint State = 0;
 
  State = FSM[State][Index_for(Input)];

  if(State == (uint)(-1))

  {
    State = 0;
    return 1;
  }
  else
  
    return 0;
}


// Использование в прикладной функции
while(!terminate)
{
  if(Engine(Stream++))
    goto Found;
};
Stopped:
// Последовательность не обнаружена, работа остановлена командой

Found:
// Последовательность обнаружена
}

Я привёл основные способы реализации автоматов. Дальнейшее развитие способов реализации связано с соединениями автоматов. Это отдельная большая тема и ей будет посвящён отдельный цикл статей.

Сегодняшний обзор подошёл к концу. В следующей статье речь пойдёт об эффективности – о тех плюсах, которые можно измерить.

Автор: Александр Соловьёв

Источник