Хочу предложить Хабру свою версию нерекурсивного алгоритма генерации всех разбиений целого числа в лексикографическом порядке. Толчком послужила майская заметка. В предлагаемом алгоритме также идея переноса крайне правого элемента.
Причины по которым захотелось предложить свой вариант алгоритма в том, что во всех увиденных мной алгоритмах на каждом шагу есть поиск по массиву. Мне показалось это несколько избыточным. Сам алгоритм будем рассматривать как описание перестановки единичных кубиков (квадратиков) на плоскости (справа налево) и их периодическое рассыпание по горизонтальной оси.
Подробности ниже.
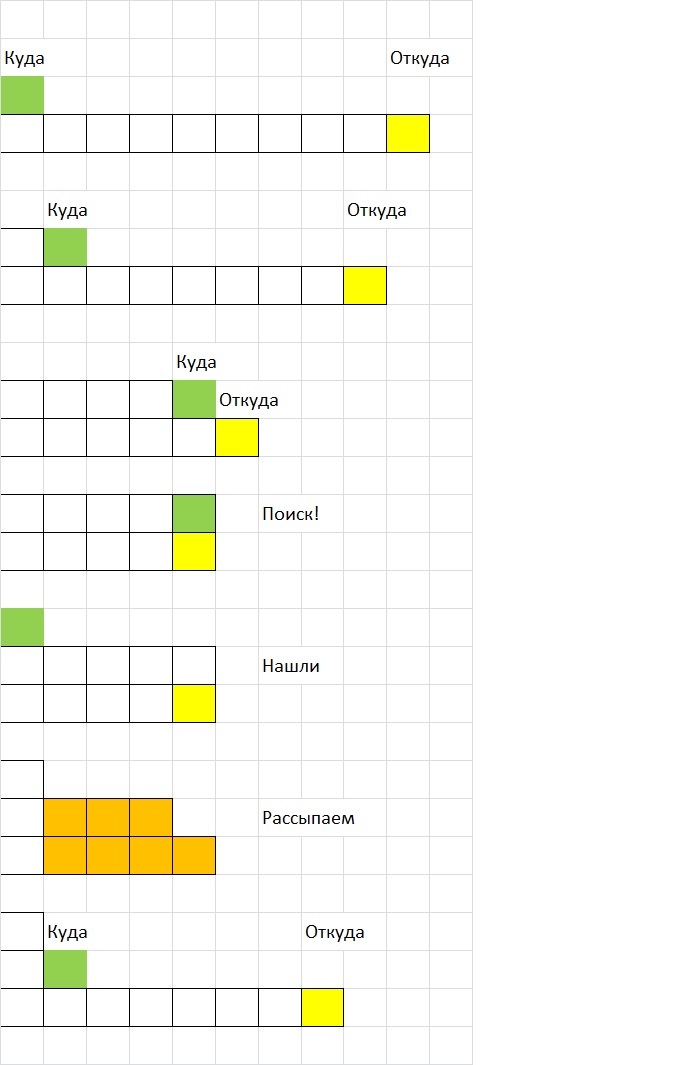
Начало Алгоритма
Имеем массив x_massiv размерности NN из 1 (квадратики все лежат в один ряд по оси X) — индекс это X координата, значение массива x_massiv это количество кубиков. Введем следующие дополнительные переменные:
- координату куда ставить кубик to_x
- координату откуда снимать кубик from_x
- количество кубиков которые надо рассыпать ost и ost1
Первое число в разбиении может быть от 2 до NN, поэтому используем цикл For hh = 2… NN
Оно может повториться в разбиении еще несколько раз, поэтому используем еще один цикл
For JJ = 1… kol_hh (kol_hh = Int(NN / hh) — целая часть) в котором формируем от одного и более элементов. Перед началом основного цикла имеем заполненный прямоугольник (размеры hh на jj). Рассчитываем значения ost,ost1 = NN — hh * jj — остатки которые надо разносить в основном цикле и начальные координаты
- from_x = NN — jj * (hh — 1)
- to_x = jj + 1
Основной цикл
Переставляем кубик из места from_x на место to_x (x_massiv(from_x)-- и x_massiv(to_x)++) проверка на выход из основного цикла по условиям:
- x_massiv(to_x) = hh
- или ost <= 1
- или x_massiv(to_x — 1) = hh And to_x = from_x
Пересчет from_x и to_x в зависимости от независимых условий:
- x_massiv(from_x) >2 условие для рассыпания
x_massiv(from_x) <=2 рассыпать не надо - Близость to_x и from_x
- размер остатка ost1
Все возможные комбинации условий (подробности в исходных кодах). Поиск по массиву нужен не всегда. Считаю это плюсом. При необходимости идет пересчет остатка разбиения ost1.
- Если необходимо, проводится поиск to_x. интервал поиска меньше чем 1..NN. to_x ищется как координата с наименьшем значением, поиск по убыванию (справа налево)
- Если необходимо, проводится рассыпание остатков, правее того места стало где больше 2 кубиков (условия видны из текста vbs скрипта и/или go программы)
конец основного цикла
конец цикла jj
конец цикла hh
Понимаю, что описание достаточно корявое, т.к. это перевод с языка программирования на естественный. Для тех кто знаком с синтаксисом Vb Vbf Vbs возможно проще сразу смотреть скрипт, для остальных — текст на go. Плюс картинка.
У меня массивы ниже начинаются с 1.
Пример алгоритма на vbs
VBS-скрипт (для Win) — запуск лучше делать как открыть в командной строке:
Dim ii , jj , kkk
Dim summ , str_rez, iii
Dim from_x , to_x
Dim ost , ost1 , flag_poisk , flag_razb
Dim kol_razb , kol_poisk
Dim hh , kol_hh
str_rez = inputbox ( "Введите число для разбиений N")
if str_rez <> vbNullString then
if IsNumeric (str_rez) then
NN = cint(str_rez)
else
WScript.Quit
end if
else
WScript.Quit
end if
ReDim x_massiv(NN)
For ii = 1 To NN - 1
x_massiv(ii) = 1
Next
str_rez = vbNullString
For iii = 1 To NN
str_rez = str_rez + "1;"
Next
'''вывод
WScript.Echo str_rez
kol_razb = 1
For hh = 2 To NN ' - 1
kol_hh = Int(NN / hh)
For jj = 1 To kol_hh
''' инициализация
For ii = 1 To jj
x_massiv(ii) = hh
Next
from_x = NN - jj * (hh - 1)
to_x = jj + 1
ost = NN - hh * jj
ost1 = ost
For ii = to_x To from_x
x_massiv(ii) = 1
Next
Do
str_rez = vbNullString
For iii = 1 To from_x
If x_massiv(iii) > 0 Then
str_rez = str_rez + CStr(x_massiv(iii)) + ";"
Else
Exit For
End If
Next
'''вывод
WScript.Echo str_rez
kol_razb = kol_razb + 1
If ost <= 1 Then
Exit Do
End If
''' перенос начинаем переставлять кубики
''' из места from_x на место to_x
x_massiv(from_x) = x_massiv(from_x) - 1
x_massiv(to_x) = x_massiv(to_x) + 1
If x_massiv(to_x) = hh Then
Exit Do
End If
If x_massiv(to_x - 1) = hh And to_x = from_x Then
Exit Do
End If
flag_poisk = False
flag_razb = False
If x_massiv(to_x) > 2 Then
If to_x + 1 = from_x Then
ost1 = x_massiv(from_x)
If ost1 = 0 Then
from_x = from_x - 1
flag_poisk = True
Else
If ost1 = 1 Then
flag_poisk = True
Else
flag_razb = True
ost1 = x_massiv(from_x)
from_x = to_x + ost1
to_x = to_x + 1
End If
End If
Else ''' to_x + 1 != from_x
flag_razb = True
ost1 = ost1 - x_massiv(to_x)
from_x = to_x + ost1
to_x = to_x + 1
End If
Else
If x_massiv(from_x) = 0 Then
from_x = from_x - 1
End If
If to_x + 1 < from_x Then
to_x = to_x + 1
ost1 = ost1 - 2
Else
flag_poisk = True
End If
End If
If flag_poisk Then
kol_poisk = kol_poisk + 1
flag_poisk = False
summ = x_massiv(from_x)
''поиск to_x. интервал меньше чем 1..NN
For kkk = from_x - 1 To jj + 1 Step -1
summ = summ + x_massiv(kkk)
If x_massiv(kkk) < x_massiv(kkk - 1) Then
to_x = kkk
ost1 = summ
flag_poisk = True
Exit For
End If
Next
If Not flag_poisk Then
to_x = jj + 1
ost1 = ost
End If
End If ''' flag_poisk
If flag_razb Then '' рассыпаем
For kkk = to_x To from_x
x_massiv(kkk) = 1
Next
End If
Loop
Next
Next
MsgBox "Разбиений = " + CStr(kol_razb) + vbCrLf + " Поисков =" + CStr(kol_poisk)
Пример алгоритм на golang (как умею, языком только балуюсь)
Запустить можно на golang.org/#:
//разбиение целого числа в лексикографическом порядке
// razbien_int project main.go
package main
import (
"fmt"
)
func main() {
var massiv [100]int32
var NN, HH, kol_HH int32
var ii, jj, kol_poisk, kol_per, kol_rez int32
var from_x, to_x int32 // указатели откуда и куда переносим 1
var ost, ost1, summ int32
var flag_poisk, flag_per byte
NN = 20 // число которое разбиваем <=100
kol_poisk = 0 //кол-во поисков
kol_per = 0 //кол-во рассыпаний переукладок
fmt.Println("NN =", NN)
for ii = 1; ii <= NN; ii++ {
massiv[ii] = 1
}
from_x = NN
/// pr_mass(NN)
fmt.Println(massiv[1:NN]) // печать 1
kol_rez = 1 /// первый результат
for HH = 2; HH <= NN; HH++ { // величина превого элемента в разбиении
kol_HH = NN / HH // максимальное число повторов первого элемента HH
for jj = 1; jj <= kol_HH; jj++ {
// ini 1 заполнение первым элементом
for ii = 1; ii <= jj; ii++ {
massiv[ii] = HH
}
from_x = NN - jj*(HH-1)
to_x = jj + 1
ost = NN - HH*jj
ost1 = ost
// ini 2 заполнение хвоста 1
for ii = to_x; ii <= from_x; ii++ {
massiv[ii] = 1
}
// сформирован массив из первых значений HH и 1
// основной цикл
for {
fmt.Println(massiv[1 : from_x+1]) // печать
///pr_mass(from_x)
kol_rez++
if ost <= 1 {
break
}
massiv[from_x]--
massiv[to_x]++
if massiv[to_x] == HH {
break
}
if massiv[to_x-1] == HH && to_x == from_x {
break
}
flag_poisk = 0
flag_per = 0
if massiv[to_x] > 2 {
if to_x+1 == from_x {
ost1 = massiv[from_x]
if ost1 == 0 {
from_x--
flag_poisk = 1
} else {
if ost1 == 1 {
flag_poisk = 1
} else {
flag_per = 1
ost1 = massiv[from_x]
from_x = to_x + ost1
to_x++
}
}
} else { /// to_x+1 != from_x
flag_per = 1
ost1 = ost1 - massiv[to_x]
from_x = to_x + ost1
to_x++
}
} else { /// <=2
if massiv[from_x] == 0 {
from_x--
}
if to_x+1 < from_x {
to_x++
ost1 = ost1 - 2
} else {
flag_poisk = 1
}
}
if flag_poisk == 1 {
kol_poisk++
flag_poisk = 0
summ = massiv[from_x]
for kkk := from_x - 1; kkk >= jj+1; kkk-- {
summ = summ + massiv[kkk]
if massiv[kkk] < massiv[kkk-1] {
to_x = kkk
ost1 = summ
flag_poisk = 1
break
}
}
if flag_poisk == 0 {
to_x = jj + 1
ost1 = ost
}
}
if flag_per == 1 {
kol_per++ /// рассыпаем
for kkk := to_x; kkk <= from_x; kkk++ {
massiv[kkk] = 1
}
}
}
}
}
fmt.Println("Число разбиений =", kol_rez)
fmt.Println("количество поисков =", kol_poisk)
fmt.Println("количество рассыпаний =", kol_per)
}
Наблюдение
- Доля поисков в общем числе разбиений немногим более одной трети (для чисел менее 30)
- С ростом разбиваемого числа доля поисков снижается до одной четверти (для чисел более 70), за 100 не переходил
- Возможно, снижение числа поисков несколько ускоряет алгоритм, но с другой стороны делает его чуть сложнее
Для тех кто добрался до конца заметки: если рассматривать количество кубиков по оси Y (вертикальной), то их количество будет тоже лексикографическим разбиением числа, но уже в обратном порядке. Это меня удивляет.
Ссылки:
[1] В.Липский. Комбинаторика для программистов. (Москва, издательство Мир, 1988. стр 63)
Автор: SemenovVV






