Первая часть публикации вызвала определённый интерес, пришёл ряд откликов, среди которых есть один, который хочется отметить особо: «жаль, нельзя скачать с гитхаба половину автомата и допилить под свою задачу, все надо делать самостоятельно. Если бы был некий стандарт записи автомата в какой-нибудь xml, позволяющий обмен автоматными алгоритмами, плюс некая «стандартная библиотека», возможно, все бы было иначе […] речь идёт о выдумывании какого-то «обобщенного состояния» и «обобщенного автомата», построении библиотеки таких автоматов с возможностью их комбинировать так же просто, как вызываются функции в языках». Отвечу читателю и всем, кто знаком с темой программных автоматов, но не удовлетворён нынешним положением дел (а оно в целом неудовлетворительное): мы обратимся именно к такой постановке вопроса, после того как будет достаточно очерчен предмет разговора.
Сегодняшняя статья посвящена теоретическим, идейным и психологическим аспектам автоматов. Рассмотрев их, мы снова вернёмся на прагматические позиции, которые были заявлены в начале цикла публикаций.
_________________________________________________________________________________
«Дисплей», рассмотренный в предыдущей статье, это сквозной пример, который словно нитью свяжет весь цикл. Мне не хотелось делать статью, рассчитанную на «подготовленного читателя», но в то же время не хочется давать примеры типа «пусть у нас есть кнопка и светодиод», потому что такие примеры, конечно, дают представление об автоматах, но они не дают никакого представления о преимуществе автоматного подхода.
Для тех, кто наткнулся на неочевидные моменты, просьба скидывать конкретные труднопроходимые места в коменты, прямо в виде коротких цитаток. Тема автоматного проектирования и тема автоматной реализации ещё будут затронуты, и ваши пожелания лягут в основу демонстрационного и поясняющего материала. Так же я слегка поправил первую статью, подробней расписав ход рассуждений при разработке операционного и управляющего автоматов (см, начиная с рисунка 10 а).
Желающим подтянуть матчасть советую ознакомиться с лекциями. Это качественный обзорный и учебный материал, охватывающий многие аспекты математических автоматов.
Автомат vs автомат
Специалисты приводят довольно разветвлённую классификацию автоматов: детерминированные и недетерминированные, конечные и бесконечные, Мили и Мура, синхронные и асинхронные, и т.д. Однако с точки зрения пользователя это всё равно, как если бы человек хотел решить для себя — нужен ли ему личный автомобиль в мегаполисе, а ему рассказывали бы о количестве цилиндров, и инжекторе.
Как популяризатор отмечу, что с точки зрения использования автоматы делятся на две связанные категории:
- автоматы как математическая абстракция, отнесём сюда и способы реализации автоматов.
- автоматы как набор техник и подходов для проектирования цифровых логических устройств (схем и программ), также основанных на математике.
Связь между этими подходами несложно проиллюстрировать:
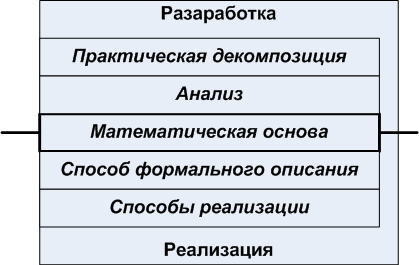
Рисунок 1. Автоматное проектирование и автоматная реализация
Насколько стало понятно из общения с читателями, существует категория формалистов, людей рассматривающих автоматы как:
- сущности, описание которых должно строго укладываться в рамки UML State Diagrams или аналогичных способов описания, то есть иметь набор узлов, заданных в виде отдельных функций, набор сигналов, и формализованную таблицу, определяющую связи между ними.
- понятие автоматно реализованной программы строго ограничивается принадлежностью к одной из техник реализации — boost.statechart, visualState, и т.д.
Очевидно, что такой подход сужает пространство возможностей, которые открываются благодаря автоматно-ориентированной парадигме, и такое отношение к автоматам можно объяснить только лишь нехваткой научно-популярного материала, что поправимо.
То, ради чего хочется использовать автоматы – простота и в то же время глубина проектирования. В предыдущей части было показано, что в основе автоматно-ориентированного проектирования модулей, лежит разбиение задачи на операционный автомат (ОА) и управляющий автомат (УА), причём операционный автомат в свою очередь может быть повторно разбит на операционный автомат нижнего уровня и его управляющий автомат.
Операционный автомат это полуфабрикат, который может оптимально выполнять некоторое действие, но при этом его «не волнует» когда выполнять это действие и с какими параметрами. Операционный автомат может делать это с любыми допустимыми параметрами. Отличный пример операционного автомата АЛУ.
В свою очередь, параметризация и запуск операционного автомата ложится на плечи управляющего автомата.Многоступенчатость разбиения позволяет избежать получения сложного управляющего автомата с не очевидной, хотя и железной логикой, заменив его несколькими простыми управляющими автоматами с максимально понятным функционированием.
Реализация управляющего автомата при этом может быть совсем не автоматной, или быть автоматной, но без таких атрибутов как: состояния закатанные в отдельные функции, таблицы сигналов и соответствующих им переходов. И, наконец, замечу, что любая программа является автоматом, и тем не менее не все программы являются автоматно реализованными.
Но в таком случае, что подразумевать под автоматно реализованной программой?
Реализация: автоматная vs не автоматная.
Главным атрибутом автоматно реализованной программы является:
- наличие явно выделенных и чётко ограниченных состояний. В процессе функционирования программа всегда находится в одном из состояний.
- текущее состояние программы описывается одной единственной переменной, которая называется Внутреннее состояние автомата.
Данное определение, так сказать инвариант, воплощение которого может быть различным. В разделе Способы реализации автоматных программ мы рассмотрим ряд примеров, которые проиллюстрируют сказанное, но в общем суть понятна.
Теперь есть чёткий критерий, по которому мы относим программы к автоматно реализованным программам, но кто-то спросит: в чём прикол автоматной реализации, почему в некоторых случаях она более ценна?
Главное, что отличает автоматно-реализованные алгоритмы от реализованных неавтоматно лежит в сфере нашей психики, а точнее того как мы мыслим. Как метко заметил коллега:
«Человеческий разум устроен так, что ему проще понимать алгоритмы, которым скармливают данные на входе и получают данные на выходе, и результат зависит только от входа, но не от внутреннего состояния. Такие «чистые функции» (назовём их аналитические прим.авт.) проще понимать, тестировать и использовать повторно».
Поведение аналитической функции можно представить в виде некоторой таблицы или графика: есть что-то на входе и есть однозначное соответствие на выходе. Однако цифровые устройства в большинстве таковы, что используя в качестве кирпичиков аналитические функции, в результате мы всё равно получаем программу, поведение которой зависит уже и от внутреннего состояния. То есть, использование аналитических функций не решает проблему «понимаемости», перемещая её на другой уровень!
Чтобы проиллюстрировать термин «понимаемость» и особенности человеческого , предлагаю рассмотреть, как записывается один и тот же абстрактный алгоритм, реализованный автоматно и неавтоматно.
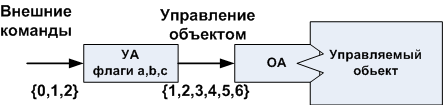
а)
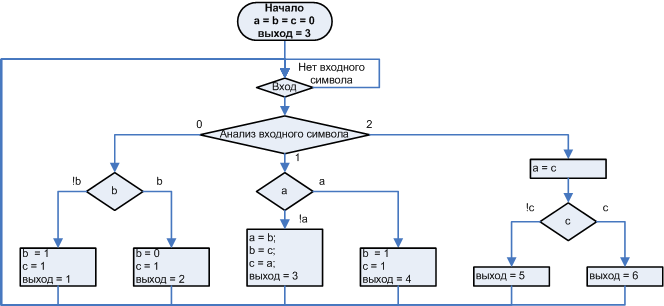
б)
Рисунок 2. Обобщённый пример управляющего устройства (а) и граф-схема описывающая работу этого устройства (б).
Некая программа предназначена для управления неким устройством. Как показано на рис 2 а, непосредственно «железом» управляет не уточняемый ОА, которым управляет УА, алгоритм работы которого изображён на рис. 2 (б). УА обрабатывает внешние команды, условно обозначаемые набором символов {0,1,2}, и транслирует их в набор микроинструкций, управляющих операционным автоматом. Под микроинструкцией я подразумеваю нужный для получения эффекта набор команд. Каждый набор микроинструкций условно обозначен символом {1,2,3,4,5,6}. Флаги {a,b,c} управляющего автомата отслеживают состояние управляемого объекта, и, соответственно, определяют режимы обработки входной команды.
Поскольку это цифровое устройство с памятью, описанный рис 2 алгоритм фактически является автоматом, несмотря на то, что реализация алгоритма неавтоматная. Это приводит к тому, что в нем нет явно выделенных состояний, в результате чего текущее состояние неявно определяется флагами. При этом описание программы граф-схемой само по себе не противоречит автоматному принципу. Существуют техники, позволяющие в некоторых случаях по алгоритму, описанному граф-схемой математически получать соответствующую диаграмму состояний и переходов. Граф-схемой, наконец, можно описать автоматно-реализованную программу, будет и такой пример. Проблема не в граф-схеме, а в неавтоматности реализации. Неавтоматная реализация ухудшает понимаемость и не даёт ключа к анализу динамических систем. Вот, что я имею в виду: это очень простой пример, но здесь нельзя однозначно сказать, какой выходной сигнал будет соответствовать входному сигналу 0, потому что это будет зависеть от состояния флагов, а точнее флага b, которое в свою очередь зависит от того, что было на входе ранее. Точно также непросто с ходу сказать, какая выходная последовательность будет соответствовать входной последовательности: 2,1,0,2,1,0. Для этого нужно фактически выполнить алгоритм.
Для того чтобы дать полное соответствие входных и выходных сигналов, то есть описать функцию в виде таблицы, потребуется произвести тотальное тестирование, да ещё и к тому же результат получится в виде двухсигнальных последовательностей, в которых по очереди перебираются всевозможные входные комбинации.
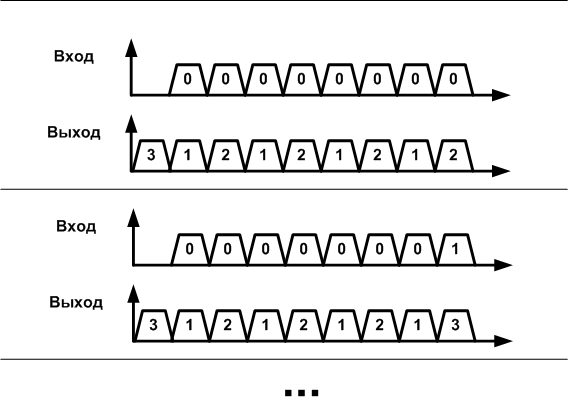
Рисунок 3. Временная диаграмма – способ описания поведения систем с памятью.
Поскольку три бинарных флага позволяют отслеживать не более (но возможно и не менее) 8ми предшествовавших символов, то для алфавита из 3х входных символов, чтобы описать все возможные варианты нам потребуется привести 6561 диаграмм, так называемая мощность произведения множества входных сигналов и множества состояний, которая с ростом числа состояний и размера алфавита входных сигналов растёт геометрически.
Автоматная реализация программы позволяет описать её при помощи диаграммы состояний, а диаграмма состояний и переходов даёт кардинально иной подход к анализу динамических систем с памятью. Построим автомат, который реализует изображённый на рис 2 б алгоритм (я не буду здесь уточнять как, это тема другого разговора), и который описывается диаграммой состояний и переходов изображённой на рис 4. Название состояния на диаграмме совпадает с выходным символом, когда автомат в этом состоянии.
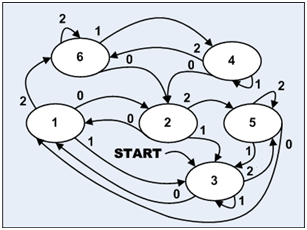
Рисунок 4. Диаграмма состояний и переходов соответствующая изображённому на рис 2 алгоритму.
Пользоваться этой диаграммой очень удобно, поскольку на переходы влияют только входные символы, нет никаких дополнительных условий. Иными словами, чтобы анализировать реакцию на входной символ для реализации рис 2 нужно иметь перед глазами текущее состояние флагов, в каждой итерации новое, а для того чтобы анализировать поведение устройства реализованного как показано на рис 4, не нужно ничего кроме этой диаграммы.
Это важное преимущество автоматного подхода, называемое:
Взгляд на динамические процессы вне временной оси.
Человеческий устроен так, что легче работать с таблицей цифр, чем если ту же таблицу показывать по одной цифре по очереди. В первом случае человек способен выявлять сложные закономерности, во втором едва ли сможет определить какую-либо закономерность, кроме простейших, даже если прокручивать таблицу циклически.
Рассмотрим пример, пусть у нас есть последовательность команд
Set_position(6,0);
Line_to (1,0); Line_to (1,1); Line_to (-1,2); Line_to (4,0);
Line_to (1,-3); Line_to (3,0); Line_to (0,6); Line_to (-11,0);
Line_to (-1,1); Line_to (-2,0); Line_to (3,-2); Line_to (0,-2);
Line_to (1,2); Line_to (2,0); Line_to (-1,-2); Line_to (1,-1);Согласитесь, каждое из действий отличается простотой замысла. Однако, не выполнив всех действий нельзя сказать, что у нас получится. Результат выполнения этого алгоритма приведён, на рис. 5 а
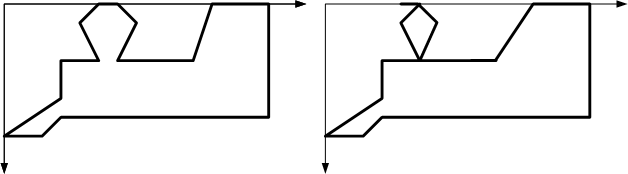
а) б)
Рисунок 5. Результат выполнения последовательности команд (а), и результат выполнения этой же последовательности, если допущена ошибка(б).
В то же время, ошибись я в расчётах, и укажи, например, в первом операторе второй строки вместо (1,-3) значение (2,-3) результат работы был бы иной (5 б), но глядя на текст программы этого нельзя понять. И это простой случай, когда результат можно увидеть сразу после выполнения. Если бы мы видели результат в виде отдельно взятой линии в каждый момент времени, или имели дело не с графикой, а с цифрами, наша ошибка была бы не столь очевидна.
Это непростой для человеческого вид информации, называемый динамический процесс, как последовательность действий (в примере отдельные линии), дающих в результате наложения некоторый предполагаемый результат (в примере рисунок).
Неплохим примером взгляда на динамические процессы вне временной оси является анализ сигналов в частотной области. Рассмотрим сигнал рис 6. В чём-то его можно сравнить с временной диаграммой автомата. Это тоже последовательность действий: сигнал пересёк 0, пошёл вверх, достиг максимума, пошёл вниз, снова пересёк 0.
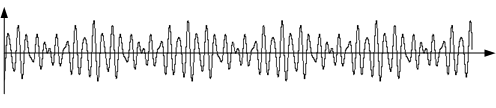
Рисунок 6. График сигнала, аналог временной диаграммы для автоматов.
Очевидно, что это периодический сигнал, можно даже угадать, что он состоит из нескольких синусоид, но нам сложно сказать из каких.
В то же время спектр прямо даёт нам представление о структуре сигнала.
Рисунок 7. Спектр сигнала изображённого на рис 6.
Спектр можно сравнить с автоматной диаграммой вот в каком отношении: он содержит статическое описание того, что лежит в основе процесса, протекающего во времени. И спектр и диаграмма состояний и переходов дают возможность анализировать процесс вне временной оси, охватывая его в целом, а не как последовательность шагов.
Немного математики.
Диаграмма состояний и переходов, как строгая математическая категория даёт возможность углублённого анализа.
Проанализируем описанный диаграммой состояний и переходов рис 5 процесс. Для этого нам потребуется понятие изоморфного автомата. Изоморфные автоматы — математический термин, означающий автоматы, которые фактически являются одним и тем же автоматом, с переименованными состояниями и/или сигналами.
Рисунок 8. Изоморфные автоматы.
Из условий задачи следует, что мы ничего не знаем о процессах, которые моделирует алгоритм рис. 2 б. Тем не менее, анализ приведённой на рис. 4 диаграммы позволяет выделить два очень похожих кластера, переключение между которыми производится в основном сигналом 0.
Построим автомат, изоморфный исходному, но у которого переименованы номера состояний как это показано на рис 9 и очертим на нём указанные кластеры. В кластере с состояниями 4,5,6 в скобках указаны идентичные состояния первого кластера.
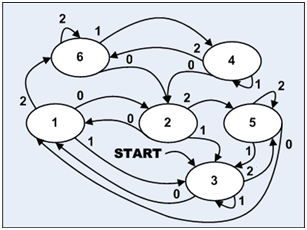
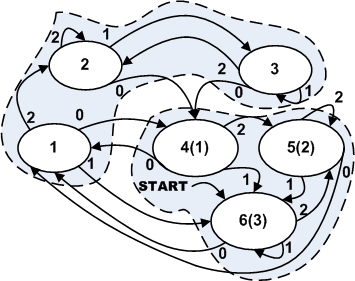
Рисунок 9. Автомат, изоморфный изображённому на рис.4
Декомпозируем (разобьём) исходный автомат на два параллельных автомата, как показано на рис. 10.
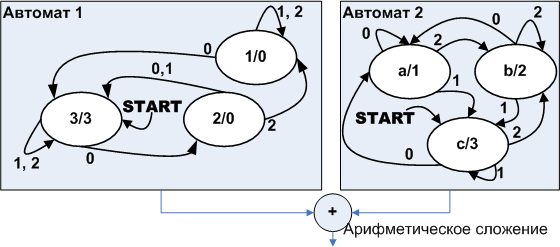
Рисунок 10. Параллельная декомпозиция автомата показанного на рис 9.
Выходной символ каждого из автоматов приведён через слеш после названия состояния. Выходные символы полученных автоматов арифметически складываются, давая на выходе символы от 1 до 6, полностью соответствующие символам на выходе исходного автомата при таких же входных данных. Такое соединение автоматов называется параллельная композиция.
Обратите внимание на Автомат 2. В каком бы состоянии он не находился, входной символ 0, приводит к появлению на выходе символа 1, входной символ 1 к появлению на выходе символа 3, а символ 2 к появлению символа 2. То есть, фактически это комбинационная схема, массив выходных символов, а индекс массива — символ на входе. Изобразим автомат как это показано на рис. 11
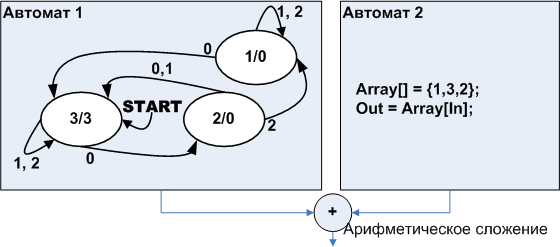
Рисунок 11. Автомат эквивалентный автомату изображённому на рис. 10
Поскольку выходные символы у нас кодировали некий набор микроинструкций, может показаться, что арифметические преобразования здесь неуместны, однако, если посмотреть на проблему глазами математика и представить, что у нас есть массив реализованных микроинструкций, в котором каждая микроинструкция имеет индекс, в этом случае корректность произведённых нами преобразований не вызывает сомнений.
Подчеркну особо, поскольку символы 0,1,2 на входе и символы 1,2,3 на выходе относятся к разным алфавитам, то нельзя просто так взять и подать символ 1 с выхода обратно на вход. Однако, могут быть такие автоматы, в которых входной и выходной символы принадлежат одному алфавиту и в этом случае выходные символы автомата можно подавать на его вход. Это называется композиция с обратной связью. Таким композициям посвящён параграф 4.7 лекций.
Из условия задачи не была известна природа объекта, который моделируется алгоритмом
рис. 2 б, и тем не менее, анализируя и декомпозируя автоматы, мы установили что в основе моделируемого явления лежат на самом деле два независимых процесса, которые вносят свой вклад в конечный результат. И хотя в случае абстрактного примера это ни даёт ничего, кроме интересного наблюдения, в случае конкретной задачи приведённый анализ может раскрыть неочевидные аспекты моделируемого явления, поэтому он интересен не только с точки зрения программирования, но и с инженерной точки зрения. Для инженера понимание процессов лежащих в основе явления может скорректировать взгляд на разрабатываемое устройство и получить оригинальное, бьющее в самую суть техническое решение.
Рассмотренный пример затрагивает ещё одно важное и полезное свойство автоматов, понятие эквивалентных автоматов. Дело в том, что может существовать сколь угодно много автоматов, с разным количеством состояний (т.е. речь идёт не об изоморфных автоматах), которые на одну и ту же входную последовательность дадут одинаковый отклик. Соответственно, если поместить их в «чёрный ящик», то нельзя будет отличить их, подавая на вход разные последовательности и анализируя отклик. Одни автоматы при этом будут более «расточительны» с точки зрения количества внутренних состояний, другие более «экономны». Среди всего множества эквивалентных автоматов будет автомат с минимально возможным количеством состояний, и он называется минимальный автомат. Более того, существуют алгоритмические методики получения из любого автомата эквивалентного ему минимального. Это свойство в частности означает, что при составлении диаграммы состояний и переходов не следует гнаться за минимизацией числа состояний, но следует добиться максимально ясной и полной картины. И хотя часто понимаемость и простота реализации связаны, может оказаться, что нагляднее представить результат в виде пары автоматов как в нашем примере. После этого, при помощи математических алгоритмов можно найти эквивалентный минимальный автомат.
Поскольку у меня нет замысла рассматривать в этой статье теорию автоматов, перечислю вкратце основные математические операции, которые можно выполнять над автоматами: композиция, декомпозиция, минимизация, получение автомата из микропрограммы, получение микропрограммы на основе автомата, алгебраические операции над автоматами (сложение, сравнение автоматов), построение имитирующего автомата и пр. Теоретические обоснования и методики выполнения данных преобразований можно найти, например здесь.
Подведём итог сегодняшней части. Характерная черта неавтоматного программирования, это то, что состояние программы в каждый момент времени описывается не только программным счётчиком, но и некоторым количеством внутренних флагов. Термин состояние при неавтоматном стиле программ это некое не формализуемое понятие, означающее примерно то, что программа выполняет все действия, которые требует ТЗ. И тем не менее, как это было показано выше, даже при неавтоматном стиле программы, математически она – автомат. Она обладает состояниями в математическом смысле, но состояния эти нигде не описаны. Неизвестно сколько их и какие между ними связи. Добавление каждого нового двоичного флага увеличивает количество возможных состояний геометрически. Многие новые состояния при этом будут недостижимыми состояниями, в которые программа не должна попасть никогда ни при каких условиях, но поскольку в этом случае мы не выбираем следующее состояние явно, но оно получается как суперпозиция всех флагов, при неверной логике хоть одного из флагов программа может скакать в запрещённые состояния и нет индикатора, который демонстрировал бы это. Когда мы имеем дело с флагами, которые активно меняются, а путь программы извилист и проходит множество ветвлений, то до тех пор пока не будут протестированы все варианты развилок для всех возможных входных символов, нам остаётся только верить, что после -дцатой итерации программа окажется именно в том состоянии, которое мы ожидаем.
В случае автоматной реализации состояние — математическая категория. В каждый момент времени оно однозначно определено, в частности программным счётчиком. Мы сами задаём тот набор состояний, который нужен для решения задачи управления и для каждого состояния явно выбираем исходя из потребностей какое состояние будет следующим, если придёт команда Х или Y. Если не хватает состояний, можно произвольно увеличивать их количество до требуемого, однозначно прописывая связи между ними.
Я хочу, чтоб меня поняли верно. Реализуя программу автоматно, мы тоже не застрахованы от опечаток или неверного замысла. Неправильно смоделировав устройство, можно задать переход не в то состояние, но это уже не ошибка проектирования ПО, а инженерная ошибка, т.е. это не связано с тем какой путь — автоматный или неавтоматный выбран. При неавтоматной реализации к тем же самым ошибкам моделирования и опечаткам добавляется мощный источник потенциальных логических ошибок название которому: динамический процесс как последовательность действий, дающих в результате наложения некоторый предполагаемый результат.
В следующей части мы вернёмся на твёрдую почву практических алгоритмов, устроив соревнования между двумя реализациями примера «Дисплей», одна из которых разработана автоматно, а другая нет, а так же рассмотрим итерационный процесс на примере модификации автомата для примера «Дисплей».
Список рекомендованной литературы. Если есть потрясающий сюжет про автоматы, пишите мне, я добавлю.
Лекции новичкам, тем кто подзабыл и вообще.
Очень сильные лекции с примерами
Автор: Александр Соловьёв
