Эта статья является продолжением моего введения в алгоритм A*. В ней я показал, как реализуются поиск в ширину, алгоритм Дейкстры, жадный поиск по наилучшему первому совпадению и A*. Я стремился как можно больше упростить объяснение.
Поиск по графам — это семейство схожих алгоритмов. Существует множество вариаций алгоритов и их реализаций. Относитесь к коду этой статьи как к отправной точке, а не окончательной версии алгоритма, подходящей ко всем ситуациям.
1. Реализация на Python
Ниже я объясню бо́льшую часть кода. Файл implementation.py несколько шире. В коде используется Python 3, поэтому если вы используете Python 2, то нужно будет поменять вызов super() и функцию print на аналоги из Python 2.
1.1 Поиск в ширину
Давайте реализуем на Python поиск в ширину. В первой статье показан код на Python для алгоритма поиска, но нам также нужно определить граф, с которым мы будем работать. Вот какие абстракции я использую:
Граф: структура данных, которая может сообщить о соседях каждой из точек (см. этот туториал)
Точки (локации): простое значение (int, string, tuple и т.д.), помечающее точки в графе
Поиск: алгоритм, получающий граф, начальную точку и (необязательно) конечную точку, вычисляющий полезную информацию (посещённый, указатель на родительский элемент, расстояние) для некоторых или всех точек
Очередь: структура данных, используемая алгоритмом поиска для выбора порядка обработки точек.
В первой статье я в основном рассматривал поиск. В этой статье я объясню всё остальное, необходимое для создания полностью рабочей программы. Давайте начнём с графа:
class SimpleGraph:
def __init__(self):
self.edges = {}
def neighbors(self, id):
return self.edges[id]Да, и это всё, что нам нужно! Вы можете спросить: а где же объект узла (Node)? Ответ: я редко использую объект узла. Мне кажется более проще использовать в качестве точек целые числа, строки или кортежи, а затем применять массивы или таблицы хешей, чтобы брать точки в качестве индексов.
Заметьте, что рёбра имеют направление: у нас может быть ребро из A в B, но не быть ребра из B в A. В игровых картах рёбра в основном двунаправленные, но иногда существуют односторонние двери или прыжки с уступов, которые обозначаются как направленные рёбра. Давайте создадим пример графа, где точки будут обозначены буквами A-E.
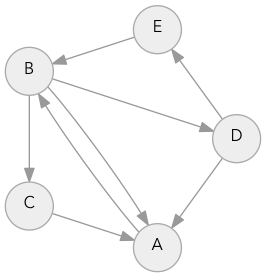
Для каждой точки нужен список точек, в которые она ведёт:
example_graph = SimpleGraph()
example_graph.edges = {
'A': ['B'],
'B': ['A', 'C', 'D'],
'C': ['A'],
'D': ['E', 'A'],
'E': ['B']
}Прежде чем воспользоваться алгоритмом поиска, нам нужно задать очередь:
import collections
class Queue:
def __init__(self):
self.elements = collections.deque()
def empty(self):
return len(self.elements) == 0
def put(self, x):
self.elements.append(x)
def get(self):
return self.elements.popleft()
Этот класс очереди является просто обёрткой встроенного класса collections.deque. В своём коде вы можете использовать непосредственно deque.
Давайте попробуем использовать наш пример графа с этой очередью и кодом поиска в ширину из предыдущей статьи:
from implementation import *
def breadth_first_search_1(graph, start):
# печать того, что мы нашли
frontier = Queue()
frontier.put(start)
visited = {}
visited[start] = True
while not frontier.empty():
current = frontier.get()
print("Visiting %r" % current)
for next in graph.neighbors(current):
if next not in visited:
frontier.put(next)
visited[next] = True
breadth_first_search_1(example_graph, 'A')
Visiting 'A'
Visiting 'B'
Visiting 'C'
Visiting 'D'
Visiting 'E'
Сетки тоже можно выразить как графы. Сейчас я определю новый граф SquareGrid, с кортежем (int, int) точек. Вместо того, чтобы хранить рёбра явным образом, мы будем вычислять их в функции neighbors.
class SquareGrid:
def __init__(self, width, height):
self.width = width
self.height = height
self.walls = []
def in_bounds(self, id):
(x, y) = id
return 0 <= x < self.width and 0 <= y < self.height
def passable(self, id):
return id not in self.walls
def neighbors(self, id):
(x, y) = id
results = [(x+1, y), (x, y-1), (x-1, y), (x, y+1)]
if (x + y) % 2 == 0: results.reverse() # ради эстетики
results = filter(self.in_bounds, results)
results = filter(self.passable, results)
return resultsДавайте проверим его на первой сетке из предыдущей статьи:
from implementation import *
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS # список long, [(21, 0), (21, 2), ...]
draw_grid(g)
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
Чтобы воссоздать пути, нам нужно сохранить точку, из которой мы пришли, поэтому я переименовал visited (True/False) в came_from (точку):
from implementation import *
def breadth_first_search_2(graph, start):
# возвращает "came_from"
frontier = Queue()
frontier.put(start)
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
return came_from
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS
parents = breadth_first_search_2(g, (8, 7))
draw_grid(g, width=2, point_to=parents, start=(8, 7))
→ → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ####↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ####↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ← ####→ ↓ ↓ ↓ ↓ ↓ ↓
→ → ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ← ← ####→ → ↓ ↓ ↓ ↓ ↓
→ ↑ ↑ ####→ ↓ ↓ ↓ ↓ ↓ ↓ ← ####↑ ← ← ← ← ← ####→ → → ↓ ↓ ↓ ↓
↑ ↑ ↑ ####→ → ↓ ↓ ↓ ↓ ← ← ####↑ ↑ ← ← ← ← ##########↓ ↓ ↓ ←
↑ ↑ ↑ ####→ → → ↓ ↓ ← ← ← ####↑ ↑ ↑ ← ← ← ##########↓ ↓ ← ←
↑ ↑ ↑ ####→ → → A ← ← ← ← ####↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####→ → ↑ ↑ ↑ ← ← ← ####↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####→ ↑ ↑ ↑ ↑ ↑ ← ← ####↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ←
→ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ←
→ → → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ←
→ → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ←
→ → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ←
В некоторых реализациях с помощью создания объекта Node используется внутреннее хранилище для хранения came_from и других значений для каждого узла графа. Вместо этого я решил использовать внешнее хранилище, создав единую таблицу хешей для хранения came_from всех узлов графа. Если вы знаете, что точки вашей карты имеют целочисленные индексы, то есть ещё один вариант — использовать для хранения came_from массив.
1.2 Ранний выход
Повторяя код предыдущей статьи, нам нужно просто добавить в основной цикл конструкцию if. Эта проверка необязательна для поиска в ширину и алгоритма Дейкстры, но обязательна для жадного поиска по наилучшему первому совпадению и A*:
from implementation import *
def breadth_first_search_3(graph, start, goal):
frontier = Queue()
frontier.put(start)
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
return came_from
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS
parents = breadth_first_search_3(g, (8, 7), (17, 2))
draw_grid(g, width=2, point_to=parents, start=(8, 7), goal=(17, 2))
. → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← . . . . ####. . . . . . .
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← . . . ####. . . . . . .
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← Z . . . ####. . . . . . .
→ → ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← . . ####. . . . . . .
. ↑ ↑ ####→ ↓ ↓ ↓ ↓ ↓ ↓ ← ####↑ ← ← . . . ####. . . . . . .
. . ↑ ####→ → ↓ ↓ ↓ ↓ ← ← ####↑ ↑ . . . . ##########. . . .
. . . ####→ → → ↓ ↓ ← ← ← ####↑ . . . . . ##########. . . .
. . . ####→ → → A ← ← ← ← ####. . . . . . . . . . . . . . .
. . . ####→ → ↑ ↑ ↑ ← ← ← ####. . . . . . . . . . . . . . .
. . ↓ ####→ ↑ ↑ ↑ ↑ ↑ ← ← ####. . . . . . . . . . . . . . .
. ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ####. . . . . . . . . . . . . . .
→ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
→ → → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
→ → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
. → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
Как мы видим, алгоритм останавливается, когда находит цель Z.
1.3 Алгоритм Дейкстры
Это добавляет сложности алгоритму, потому что мы будем начинать обрабатывать точки в улучшенном порядке, а не просто «первая вошла, первая вышла». Какой принцип мы будем использовать?
- Графу нужно знать стоимость движения.
- Очереди нужно возвращать узлы в другом порядке.
- Поиск должен отслеживать эту стоимость в графе и передавать её в очередь.
1.3.1 Граф с весами
Я собираюсь добавить функцию cost(from_node, to_node), которая сообщает нам стоимость перемещения из точки from_node в её соседа to_node. В этой карте с лесом я решил, что движение будет зависеть только от to_node, но есть и другие типы движения, использующие оба узла. Альтернативой реализации будет слияние её в функцию neighbors.
class GridWithWeights(SquareGrid):
def __init__(self, width, height):
super().__init__(width, height)
self.weights = {}
def cost(self, from_node, to_node):
return self.weights.get(to_node, 1)1.3.2 Очередь с приоритетами
Очередь с приоритетами связывает с каждым элементом число, называемое «приоритетом». При возврате элемента она выбирает элемент с наименьшим числом.
insert: добавляет элемент в очередь
remove: удаляет элемент с наименьшим числом
reprioritize: (необязательно) меняет приоритет имеющегося элемента на более низкое число.
Вот достаточно быстрая очередь с приоритетами, в которой используются двоичная куча, но не поддерживается reprioritize. Для получения правильного порядка мы используем кортеж (приоритет, элемент). При вставке элемента, который уже есть в очереди, у нас получиться дубликат. Я объясню, почему это нас устраивает, в разделе «Оптимизация».
import heapq
class PriorityQueue:
def __init__(self):
self.elements = []
def empty(self):
return len(self.elements) == 0
def put(self, item, priority):
heapq.heappush(self.elements, (priority, item))
def get(self):
return heapq.heappop(self.elements)[1]1.3.3 Поиск
Здесь есть хитрый момент реализации: поскольку мы добавляем стоимость движения, то есть вероятность повторного посещения точки с более хорошим cost_so_far. Это значит, что строка if next not in came_from работать не будет. Вместо этого нам нужно проверить, уменьшилась ли стоимость после последнего посещения. (В исходной версии статьи я не проверял это, но мой код всё равно работал. Я написал заметки об этой ошибке.)
Эта карта с лесом взята из предыдущей статьи.
def dijkstra_search(graph, start, goal):
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put(next, priority)
came_from[next] = current
return came_from, cost_so_farПосле поиска необходимо построить путь:
def reconstruct_path(came_from, start, goal):
current = goal
path = [current]
while current != start:
current = came_from[current]
path.append(current)
path.append(start) # необязательно
path.reverse() # необязательно
return path
Хотя пути лучше воспринимать как последовательность рёбер, удобнее хранить как последовательность узлов. Для создания пути начнём с конца и проследуем по карте came_from, указывающей на предыдущий узел. Когда мы достигнем начала, дело сделано. Это обратный путь, поэтому в конце reconstruct_path мы вызываем reverse(), если нужно хранить его в прямой последовательности. На самом деле иногда удобнее хранить путь в обратном виде. Кроме того, иногда удобно хранить в списке начальный узел.
Давайте попробуем:
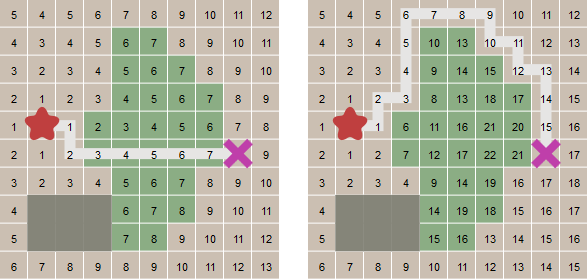
from implementation import *
came_from, cost_so_far = dijkstra_search(diagram4, (1, 4), (7, 8))
draw_grid(diagram4, width=3, point_to=came_from, start=(1, 4), goal=(7, 8))
print()
draw_grid(diagram4, width=3, number=cost_so_far, start=(1, 4), goal=(7, 8))
print()
draw_grid(diagram4, width=3, path=reconstruct_path(came_from, start=(1, 4), goal=(7, 8)))
↓ ↓ ← ← ← ← ← ← ← ←
↓ ↓ ← ← ← ↑ ↑ ← ← ←
↓ ↓ ← ← ← ← ↑ ↑ ← ←
↓ ↓ ← ← ← ← ← ↑ ↑ .
→ A ← ← ← ← . . . .
↑ ↑ ← ← ← ← . . . .
↑ ↑ ← ← ← ← ← . . .
↑ #########↑ ← ↓ . . .
↑ #########↓ ↓ ↓ Z . .
↑ ← ← ← ← ← ← ← ← .
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 18 17 14 .
1 A 1 6 11 16 . . . .
2 1 2 7 12 17 . . . .
3 2 3 4 9 14 19 . . .
4 #########14 19 18 . . .
5 #########15 16 13 Z . .
6 7 8 9 10 11 12 13 14 .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
@ @ . . . . . . . .
@ . . . . . . . . .
@ . . . . . . . . .
@ #########. . . . . .
@ #########. . @ @ . .
@ @ @ @ @ @ @ . . .
Строку if next not in cost_so_far or new_cost < cost_so_far[next] можно упростить до if new_cost < cost_so_far.get(next, Infinity), но я не хотел объяснять get() Python в прошлой статье, поэтому оставил, как есть. Можно так же использовать collections.defaultdict со значением infinity по умолчанию.
1.4 Поиск A*
И жадный поиск по наилучшему первому совпадению, и A* используют эвристическую функцию. Единственная разница заключается в том, что A* использует и эвристику, и упорядочивание из алгоритма Дейкстры. Здесь я покажу A*.
def heuristic(a, b):
(x1, y1) = a
(x2, y2) = b
return abs(x1 - x2) + abs(y1 - y2)
def a_star_search(graph, start, goal):
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
return came_from, cost_so_farДавайте попробуем:
from implementation import *
came_from, cost_so_far = a_star_search(diagram4, (1, 4), (7, 8))
draw_grid(diagram4, width=3, point_to=came_from, start=(1, 4), goal=(7, 8))
print()
draw_grid(diagram4, width=3, number=cost_so_far, start=(1, 4), goal=(7, 8))
. . . . . . . . . .
. ↓ ↓ ↓ . . . . . .
↓ ↓ ↓ ↓ ← . . . . .
↓ ↓ ↓ ← ← . . . . .
→ A ← ← ← . . . . .
→ ↑ ← ← ← . . . . .
→ ↑ ← ← ← ← . . . .
↑ #########↑ . ↓ . . .
↑ #########↓ ↓ ↓ Z . .
↑ ← ← ← ← ← ← ← . .
. . . . . . . . . .
. 3 4 5 . . . . . .
3 2 3 4 9 . . . . .
2 1 2 3 8 . . . . .
1 A 1 6 11 . . . . .
2 1 2 7 12 . . . . .
3 2 3 4 9 14 . . . .
4 #########14 . 18 . . .
5 #########15 16 13 Z . .
6 7 8 9 10 11 12 13 . .
1.4.1 Спрямлённые пути
Если вы будете реализовывать этот код в собственном проекте, то можете обнаружить, что часть путей не такая «прямая», как хотелось бы. Это нормально. При использовании сеток, а в особенности сеток, в которых каждый шаг имеет одинаковую стоимость движения, у вас получатся равноценные варианты: многие пути имеют совершенно одинаковую стоимость. A* выбирает один из множества кратких путей, и очень часто он выглядит не очень красиво. Можно применить быстрый хак, устраняющий равноценные варианты, но он не всегда полностью подходит. Лучше будет изменить представление карты, что позволит намного ускорить A* и создавать более прямые и приятные пути. Однако это подходит для статичных карт, в которых каждый шаг имеет одну стоимость движения. Для демо на моей странице я использую быстрый хак, но он работает только с моей медленной очередью с приоритетами. Если переключиться на более быструю очередь с приоритетами, то потребуется другой быстрый хак.
2 Реализация на C++
Примечание: для выполнения части кода примера необходимо добавить redblobgames/pathfinding/a-star/implementation.cpp. Я использую для этого кода C++11, поэтому если вы используете более старую версию стандарта C++, то придётся частично его изменить.
2.1 Поиск в ширину
Сначала изучите раздел о Python. В этом разделе будет код, но не будет тех же объяснений. Сначала добавим общий класс графа:
template<typename L>
struct SimpleGraph {
typedef L Location;
typedef typename vector<Location>::iterator iterator;
unordered_map<Location, vector<Location> > edges;
inline const vector<Location> neighbors(Location id) {
return edges[id];
}
};
и тот же пример графа из кода на Python, использующий для пометки точек char:
SimpleGraph<char> example_graph {{
{'A', {'B'}},
{'B', {'A', 'C', 'D'}},
{'C', {'A'}},
{'D', {'E', 'A'}},
{'E', {'B'}}
}};Вместо определения класса очереди мы используем класс из стандартной библиотеки C++. Теперь мы можем попробовать выполнить поиск в ширину:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
template<typename Graph>
void breadth_first_search(Graph graph, typename Graph::Location start) {
typedef typename Graph::Location Location;
queue<Location> frontier;
frontier.push(start);
unordered_set<Location> visited;
visited.insert(start);
while (!frontier.empty()) {
auto current = frontier.front();
frontier.pop();
std::cout << "Visiting " << current << std::endl;
for (auto& next : graph.neighbors(current)) {
if (!visited.count(next)) {
frontier.push(next);
visited.insert(next);
}
}
}
}
int main() {
breadth_first_search(example_graph, 'A');
}
Visiting A
Visiting B
Visiting C
Visiting D
Visiting E
Код немного длиннее, чем на Python, но это вполне нормально.
Как насчёт сеток квадратов? Я определю ещё один класс графа. Заметьте, что он не связан с предыдущим классом графа. Я использую шаблоны, а не наследование. Граф должен только обеспечить typedef Location и функцию neighbors.
struct SquareGrid {
typedef tuple<int,int> Location;
static array<Location, 4> DIRS;
int width, height;
unordered_set<Location> walls;
SquareGrid(int width_, int height_)
: width(width_), height(height_) {}
inline bool in_bounds(Location id) const {
int x, y;
tie (x, y) = id;
return 0 <= x && x < width && 0 <= y && y < height;
}
inline bool passable(Location id) const {
return !walls.count(id);
}
vector<Location> neighbors(Location id) const {
int x, y, dx, dy;
tie (x, y) = id;
vector<Location> results;
for (auto dir : DIRS) {
tie (dx, dy) = dir;
Location next(x + dx, y + dy);
if (in_bounds(next) && passable(next)) {
results.push_back(next);
}
}
if ((x + y) % 2 == 0) {
// эстетическое улучшение для сеток квадратов
std::reverse(results.begin(), results.end());
}
return results;
}
};
array<SquareGrid::Location, 4> SquareGrid::DIRS {Location{1, 0}, Location{0, -1}, Location{-1, 0}, Location{0, 1}};
Во вспомогательном файле implementation.cpp я определил функцию для отрисовки сеток:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
SquareGrid grid = make_diagram1();
draw_grid(grid, 2);
}
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
Давайте ещё раз выполним поиск в ширину, отслеживая came_from:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
template<typename Graph>
unordered_map<typename Graph::Location, typename Graph::Location>
breadth_first_search(Graph graph, typename Graph::Location start) {
typedef typename Graph::Location Location;
queue<Location> frontier;
frontier.push(start);
unordered_map<Location, Location> came_from;
came_from[start] = start;
while (!frontier.empty()) {
auto current = frontier.front();
frontier.pop();
for (auto& next : graph.neighbors(current)) {
if (!came_from.count(next)) {
frontier.push(next);
came_from[next] = current;
}
}
}
return came_from;
}
int main() {
SquareGrid grid = make_diagram1();
auto parents = breadth_first_search(grid, std::make_tuple(7, 8));
draw_grid(grid, 2, nullptr, &parents);
}
→ → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ####↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ####↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ← ####→ ↓ ↓ ↓ ↓ ↓ ↓
→ → ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← ← ← ####→ → ↓ ↓ ↓ ↓ ↓
→ ↑ ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ####↑ ← ← ← ← ← ####→ → → ↓ ↓ ↓ ↓
↑ ↑ ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ← ← ####↑ ↑ ← ← ← ← ##########↓ ↓ ↓ ←
↑ ↑ ↑ ####→ ↓ ↓ ↓ ↓ ← ← ← ####↑ ↑ ↑ ← ← ← ##########↓ ↓ ← ←
↓ ↓ ↓ ####→ → ↓ ↓ ← ← ← ← ####↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####→ → * ← ← ← ← ← ####↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####→ ↑ ↑ ↑ ← ← ← ← ####↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ← ←
↓ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ← ← ← ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ← ←
→ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ← ← ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ← ←
→ → → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ← ←
→ → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ← ←
→ → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ← ← ←
В некоторых реализациях используется внутреннее хранилище и создаётся объект Node для хранения came_from и других значений для каждого узла графа. Я предпочёл использовать внешнее хранилище, создав единый std::unordered_map для хранения came_from для всех узлов графа. Если вы знаете, что точки вашей карты имеют целочисленные индексы, то есть ещё один вариант — использовать одномерный или двухмерный массив/вектор для хранения came_from и других значений.
2.1.1 TODO: struct точек
В этом коде я использую std::tuple C++, потому что я использовал кортежи в моём коде на Python. Однако кортежи незнакомы большинству программистов на C++. Будет немного более длинно определять struct с {x,y}, потому что потребуется определить конструктор, конструктор копирования, оператор присвоения и сравнение равенства вместе с хеш-функцией, но такой код будет более привычен большинству программистов на C++. Нужно будет его изменить.
Ещё один вариант (я использую его в своём коде) — кодировать {x,y} как int. T Если код A* всегда имеет плотное множество целочистеллых значений вместо произвольных типов Location, это позволяет использовать дополнительные оптимизации. Можно использовать для различных множеств массивы, а не таблицы хешей. Можно оставить большинство из них неинициализированными. Для тех массивов, которые нужно каждый раз инициализировать заново, можно сделать их постоянными для вызовов A* (возможно, с помощью локального хранилища потоков) и инициализировать заново только те части массива, которые использовались в предыдущем вызове. Это более сложная техника, которую я не хочу использовать в туториале начального уровня.
2.2 Ранний выход
Как и в версии под Python нам нужно всего лишь добавить к функции параметр и проверять основной цикл:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
template<typename Graph>
unordered_map<typename Graph::Location, typename Graph::Location>
breadth_first_search(const Graph& graph,
typename Graph::Location start,
typename Graph::Location goal) {
typedef typename Graph::Location Location;
queue<Location> frontier;
frontier.push(start);
unordered_map<Location, Location> came_from;
came_from[start] = start;
while (!frontier.empty()) {
auto current = frontier.front();
frontier.pop();
if (current == goal) {
break;
}
for (auto& next : graph.neighbors(current)) {
if (!came_from.count(next)) {
frontier.push(next);
came_from[next] = current;
}
}
}
return came_from;
}
int main() {
SquareGrid grid = make_diagram1();
auto parents = breadth_first_search(grid, SquareGrid::Location{8, 7}, SquareGrid::Location{17, 2});
draw_grid(grid, 2, nullptr, &parents);
}
. → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← . . . . ####. . . . . . .
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← . . . ####. . . . . . .
→ → → → → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← . . . ####. . . . . . .
→ → ↑ ####↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ← ← ← ← ← ← . . ####. . . . . . .
. ↑ ↑ ####→ ↓ ↓ ↓ ↓ ↓ ↓ ← ####↑ ← ← . . . ####. . . . . . .
. . ↑ ####→ → ↓ ↓ ↓ ↓ ← ← ####↑ ↑ . . . . ##########. . . .
. . . ####→ → → ↓ ↓ ← ← ← ####↑ . . . . . ##########. . . .
. . . ####→ → → * ← ← ← ← ####. . . . . . . . . . . . . . .
. . . ####→ → ↑ ↑ ↑ ← ← ← ####. . . . . . . . . . . . . . .
. . ↓ ####→ ↑ ↑ ↑ ↑ ↑ ← ← ####. . . . . . . . . . . . . . .
. ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ← ####. . . . . . . . . . . . . . .
→ ↓ ↓ ####↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
→ → → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
→ → → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
. → → ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ####. . . . . . . . . . . . . . .
2.3 Алгоритм Дейкстры
2.3.1 Граф с весами
У нас есть сетка со списком тайлов леса, стоимость движения по которым равна 5. В этой лесной карте я решил выполнять движение только в зависимости от to_node, но есть и другие типы движения, использующие оба узла.
struct GridWithWeights: SquareGrid {
unordered_set<Location> forests;
GridWithWeights(int w, int h): SquareGrid(w, h) {}
double cost(Location from_node, Location to_node) const {
return forests.count(to_node) ? 5 : 1;
}
};2.3.2 Очередь с приоритетами
Нам нужна очередь с приоритетами. В C++ есть класс priority_queue, использующий двоичную кучу, но без операции изменения приоритета. я использую пару (приоритет, элемент) для элементов очереди, чтобы получить правильный порядок. По умолчанию очередь с приоритетами C++ возвращает сначала с помощью компаратора std::less максимальный элемент. Нам нужен минимальный элемент, поэтому я использую компаратор std::greater.
template<typename T, typename priority_t>
struct PriorityQueue {
typedef pair<priority_t, T> PQElement;
priority_queue<PQElement, vector<PQElement>,
std::greater<PQElement>> elements;
inline bool empty() const { return elements.empty(); }
inline void put(T item, priority_t priority) {
elements.emplace(priority, item);
}
inline T get() {
T best_item = elements.top().second;
elements.pop();
return best_item;
}
};
В этом коде примера я оборачиваю класс C++ std::priority_queue, но думаю, будет разумно использовать этот класс без обёртки.
2.3.3 Поиск
См. карту с лесом из предыдущей статьи.
template<typename Graph>
void dijkstra_search
(const Graph& graph,
typename Graph::Location start,
typename Graph::Location goal,
unordered_map<typename Graph::Location, typename Graph::Location>& came_from,
unordered_map<typename Graph::Location, double>& cost_so_far)
{
typedef typename Graph::Location Location;
PriorityQueue<Location, double> frontier;
frontier.put(start, 0);
came_from[start] = start;
cost_so_far[start] = 0;
while (!frontier.empty()) {
auto current = frontier.get();
if (current == goal) {
break;
}
for (auto& next : graph.neighbors(current)) {
double new_cost = cost_so_far[current] + graph.cost(current, next);
if (!cost_so_far.count(next) || new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
came_from[next] = current;
frontier.put(next, new_cost);
}
}
}
}
Типы переменных cost должны совпадать с типами, используемыми в графе. Если вы используете int, то можно использовать int для переменной стоимости и приоритетов в очереди с приоритетами. Если вы используете double, то для них тоже нужно использовать double. В этом коде я использовал double, но можно было применить и int, при этом код работал бы так же. Однако если если стоимость рёбер графа хранится в double или double используется в эвристике, то и здесь нужно использовать double.
И, наконец, после поиска нужно построить путь:
template<typename Location>
vector<Location> reconstruct_path(
Location start,
Location goal,
unordered_map<Location, Location>& came_from
) {
vector<Location> path;
Location current = goal;
path.push_back(current);
while (current != start) {
current = came_from[current];
path.push_back(current);
}
path.push_back(start); // необязательно
std::reverse(path.begin(), path.end());
return path;
}
Хотя пути лучше воспринимать как последовательность рёбер, удобно хранить их как последовательность узлов. Для построения пути начнём с конца и будем следовать карте came_from, указывающей на предыдущий узел. Процесс закончится, когда мы достигнем начала. Это обратный путь, поэтому если требуется хранить его в прямом виде, то в конце reconstruct_path нужно вызвать reverse(). Иногда удобнее хранить путь в обратном виде. Иногда также полезно хранить в списке начальный узел.
Давайте попробуем:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
GridWithWeights grid = make_diagram4();
SquareGrid::Location start{1, 4};
SquareGrid::Location goal{8, 5};
unordered_map<SquareGrid::Location, SquareGrid::Location> came_from;
unordered_map<SquareGrid::Location, double> cost_so_far;
dijkstra_search(grid, start, goal, came_from, cost_so_far);
draw_grid(grid, 2, nullptr, &came_from);
std::cout << std::endl;
draw_grid(grid, 3, &cost_so_far, nullptr);
std::cout << std::endl;
vector<SquareGrid::Location> path = reconstruct_path(start, goal, came_from);
draw_grid(grid, 3, nullptr, nullptr, &path);
}
↓ ↓ ← ← ← ← ← ← ← ←
↓ ↓ ← ← ← ↑ ↑ ← ← ←
↓ ↓ ← ← ← ← ↑ ↑ ← ←
↓ ↓ ← ← ← ← ← ↑ ↑ ←
→ * ← ← ← ← ← → ↑ ←
↑ ↑ ← ← ← ← . ↓ ↑ .
↑ ↑ ← ← ← ← ← ↓ ← .
↑ ######↑ ← ↓ ↓ ← .
↑ ######↓ ↓ ↓ ← ← ←
↑ ← ← ← ← ← ← ← ← ←
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 18 17 14 15
1 0 1 6 11 16 21 20 15 16
2 1 2 7 12 17 . 21 16 .
3 2 3 4 9 14 19 16 17 .
4 #########14 19 18 15 16 .
5 #########15 16 13 14 15 16
6 7 8 9 10 11 12 13 14 15
. @ @ @ @ @ @ . . .
. @ . . . . @ @ . .
. @ . . . . . @ @ .
. @ . . . . . . @ .
. @ . . . . . . @ .
. . . . . . . . @ .
. . . . . . . . . .
. #########. . . . . .
. #########. . . . . .
. . . . . . . . . .
Результаты не полностью совпадают с результатами версии на Python, потому что для очереди с приоритетами я использую встроенные таблицы хешей, и порядок итерации по таблицам хешей не будет постоянным.
2.4 Поиск A*
A* почти полностью повторяет алгоритм Дейкстры, за исключением добавленного эвристического поиска. Заметьте, что код алгоритма может применяться не только для сеток. Знание о сетках находится в классе графа (в этом случае SquareGrids) и в функции heuristic. Если их заменить, то можно использовать код алгоритма A* с любой другой структурой графов.
inline double heuristic(SquareGrid::Location a, SquareGrid::Location b) {
int x1, y1, x2, y2;
tie (x1, y1) = a;
tie (x2, y2) = b;
return abs(x1 - x2) + abs(y1 - y2);
}
template<typename Graph>
void a_star_search
(const Graph& graph,
typename Graph::Location start,
typename Graph::Location goal,
unordered_map<typename Graph::Location, typename Graph::Location>& came_from,
unordered_map<typename Graph::Location, double>& cost_so_far)
{
typedef typename Graph::Location Location;
PriorityQueue<Location, double> frontier;
frontier.put(start, 0);
came_from[start] = start;
cost_so_far[start] = 0;
while (!frontier.empty()) {
auto current = frontier.get();
if (current == goal) {
break;
}
for (auto& next : graph.neighbors(current)) {
double new_cost = cost_so_far[current] + graph.cost(current, next);
if (!cost_so_far.count(next) || new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
double priority = new_cost + heuristic(next, goal);
frontier.put(next, priority);
came_from[next] = current;
}
}
}
}
Тип значений priority, в том числе тип, используемый для очереди с приоритетами, должен быть достаточно большим, чтобы вмещать в себя и стоимость графа (cost_t), и эвристическое значение. Например, если стоимость графа хранится в int, а эвристика возвращает double, то нужно, чтобы очередь с приоритетами могла получать double. В этом примере кода я использую double для всех трёх значений (стоимости, эвристики и приоритета), но я мог использовать и int, потому что мои стоимость и эвристика имеют значение integer.
Небольшое примечание: было бы правильнее написать frontier.put(start, heuristic(start, goal)), а не frontier.put(start, 0), но здесь это не важно, потому что приоритет начального узла не имеет никакого значения. Это единственный узел в очереди с приоритетами и он выбирается и удаляется ещё до того, как туда что-то будет записано.
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
GridWithWeights grid = make_diagram4();
SquareGrid::Location start{1, 4};
SquareGrid::Location goal{8, 5};
unordered_map<SquareGrid::Location, SquareGrid::Location> came_from;
unordered_map<SquareGrid::Location, double> cost_so_far;
a_star_search(grid, start, goal, came_from, cost_so_far);
draw_grid(grid, 2, nullptr, &came_from);
std::cout << std::endl;
draw_grid(grid, 3, &cost_so_far, nullptr);
std::cout << std::endl;
vector<SquareGrid::Location> path = reconstruct_path(start, goal, came_from);
draw_grid(grid, 3, nullptr, nullptr, &path);
}
↓ ↓ ↓ ↓ ← ← ← ← ← ←
↓ ↓ ↓ ↓ ← ↑ ↑ ← ← ←
↓ ↓ ↓ ↓ ← ← ↑ ↑ ← ←
↓ ↓ ↓ ← ← ← . ↑ ↑ ←
→ * ← ← ← ← . → ↑ ←
→ ↑ ← ← ← ← . . ↑ .
↑ ↑ ↑ ← ← ← . . . .
↑ ######↑ . . . . .
↑ ######. . . . . .
↑ . . . . . . . . .
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 . 17 14 15
1 0 1 6 11 16 . 20 15 16
2 1 2 7 12 17 . . 16 .
3 2 3 4 9 14 . . . .
4 #########14 . . . . .
5 #########. . . . . .
6 . . . . . . . . .
. . . @ @ @ @ . . .
. . . @ . . @ @ . .
. . . @ . . . @ @ .
. . @ @ . . . . @ .
. @ @ . . . . . @ .
. . . . . . . . @ .
. . . . . . . . . .
. #########. . . . . .
. #########. . . . . .
. . . . . . . . . .
2.4.1 Спрямление путей
При реализации этого кода в своём проекте вы можете заметить, что часть путей не так «пряма», как хотелось бы. Этот нормально. При использовании сеток, а в особенности сеток, в которых каждый шаг имеет одинаковую стоимость движения, то в результате получатся равноценные варианты: многие пути имеют одинаковую стоимость. A* выбирает один из множества кратчайших путей, и очень часто он выглядит не очень красиво. Можно устранить равноценные варианты с помощью быстрого хака, но он не полностью подходит. Лучше будет изменить представление карты, что намного ускорит A* и создаст более прямые и красивые пути. Однако это работает только с статичными картами, в которых каждый шаг имеет одинаковую стоимость движения. Для демо на моей странице я использовал быстрый хак, но он работает только с моей медленной очередью с приоритетами. Если вы перейдёте к более быстрой очереди с приоритетами, то вам понадобится другой быстрый хак.
2.4.2 TODO: вектор neighbors() должен передаваться
Вместо выделения и возврата каждый раз нового вектора для соседей, код A* должен выделить один вектор и каждый раз передавать его в функцию neighbors. В моих тестах это сделало код значительно быстрее.
2.4.3 TODO: устранить параметризацию шаблона
Цель этой страницы — создать простой в понимании код, и я считаю, что параметризация шаблона слишком усложняет его чтение. Вместо него я использую несколько typedef.
2.4.4 TODO: добавить требования
Существует два типа графов (взвешенные и невзвешенные), и код поиска по графу не сообщает, какой тип где требуется.
3 Реализация на C#
Это мои первые программы на C#, поэтому они могут быть нехарактерными или стилистически неправильными для этого языка. Эти примеры не так завершены, как примеры из разделов о Python и C++, но я надеюсь, что они будут полезны. Вот реализация простого графа и поиска в ширину:
using System;
using System.Collections.Generic;
public class Graph<Location>
{
// Если вы всегда используете для точек типы string,
// то здесь разумной альтернативой будет NameValueCollection
public Dictionary<Location, Location[]> edges
= new Dictionary<Location, Location[]>();
public Location[] Neighbors(Location id)
{
return edges[id];
}
};
class BreadthFirstSearch
{
static void Search(Graph<string> graph, string start)
{
var frontier = new Queue<string>();
frontier.Enqueue(start);
var visited = new HashSet<string>();
visited.Add(start);
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
Console.WriteLine("Visiting {0}", current);
foreach (var next in graph.Neighbors(current))
{
if (!visited.Contains(next)) {
frontier.Enqueue(next);
visited.Add(next);
}
}
}
}
static void Main()
{
Graph<string> g = new Graph<string>();
g.edges = new Dictionary<string, string[]>
{
{ "A", new [] { "B" } },
{ "B", new [] { "A", "C", "D" } },
{ "C", new [] { "A" } },
{ "D", new [] { "E", "A" } },
{ "E", new [] { "B" } }
};
Search(g, "A");
}
}Вот граф, представляющий сетку с взвешенными рёбрами (пример с лесом и стенами из предыдущей статьи):
using System;
using System.Collections.Generic;
// Для A* нужен только WeightedGraph и тип точек L, и карта *не*
// обязана быть сеткой. Однако в коде примера я использую сетку.
public interface WeightedGraph<L>
{
double Cost(Location a, Location b);
IEnumerable<Location> Neighbors(Location id);
}
public struct Location
{
// Примечания по реализации: я использую Equals по умолчанию,
// но это может быть медленно. Возможно, в реальном проекте стоит
// заменить Equals и GetHashCode.
public readonly int x, y;
public Location(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class SquareGrid : WeightedGraph<Location>
{
// Примечания по реализации: для удобства я сделал поля публичными,
// но в реальном проекте, возможно, стоит следовать стандартному
// стилю и сделать их скрытыми.
public static readonly Location[] DIRS = new []
{
new Location(1, 0),
new Location(0, -1),
new Location(-1, 0),
new Location(0, 1)
};
public int width, height;
public HashSet<Location> walls = new HashSet<Location>();
public HashSet<Location> forests = new HashSet<Location>();
public SquareGrid(int width, int height)
{
this.width = width;
this.height = height;
}
public bool InBounds(Location id)
{
return 0 <= id.x && id.x < width
&& 0 <= id.y && id.y < height;
}
public bool Passable(Location id)
{
return !walls.Contains(id);
}
public double Cost(Location a, Location b)
{
return forests.Contains(b) ? 5 : 1;
}
public IEnumerable<Location> Neighbors(Location id)
{
foreach (var dir in DIRS) {
Location next = new Location(id.x + dir.x, id.y + dir.y);
if (InBounds(next) && Passable(next)) {
yield return next;
}
}
}
}
public class PriorityQueue<T>
{
// В этом примере я использую несортированный массив, но в идеале
// это должна быть двоичная куча. Существует открытый запрос на добавление
// двоичной кучи к стандартной библиотеке C#: https://github.com/dotnet/corefx/issues/574
//
// Но пока её там нет, можно использовать класс двоичной кучи:
// * https://github.com/BlueRaja/High-Speed-Priority-Queue-for-C-Sharp
// * http://visualstudiomagazine.com/articles/2012/11/01/priority-queues-with-c.aspx
// * http://xfleury.github.io/graphsearch.html
// * http://stackoverflow.com/questions/102398/priority-queue-in-net
private List<Tuple<T, double>> elements = new List<Tuple<T, double>>();
public int Count
{
get { return elements.Count; }
}
public void Enqueue(T item, double priority)
{
elements.Add(Tuple.Create(item, priority));
}
public T Dequeue()
{
int bestIndex = 0;
for (int i = 0; i < elements.Count; i++) {
if (elements[i].Item2 < elements[bestIndex].Item2) {
bestIndex = i;
}
}
T bestItem = elements[bestIndex].Item1;
elements.RemoveAt(bestIndex);
return bestItem;
}
}
/* Примечание о типах: в предыдущей статье в коде Python я использовал
* для стоимости, эвристики и приоритетов просто числа. В коде C++
* я использую для этого typedef, потому что может потребоваться int, double или
* другой тип. В этом коде на C# я использую для стоимости, эвристики
* и приоритетов double. Можно использовать int, если вы уверены, что значения
* никогда не будут больше, или числа меньшего размера, если знаете, что
* значения всегда будут небольшими. */
public class AStarSearch
{
public Dictionary<Location, Location> cameFrom
= new Dictionary<Location, Location>();
public Dictionary<Location, double> costSoFar
= new Dictionary<Location, double>();
// Примечание: обобщённая версия A* абстрагируется от Location
// и Heuristic
static public double Heuristic(Location a, Location b)
{
return Math.Abs(a.x - b.x) + Math.Abs(a.y - b.y);
}
public AStarSearch(WeightedGraph<Location> graph, Location start, Location goal)
{
var frontier = new PriorityQueue<Location>();
frontier.Enqueue(start, 0);
cameFrom[start] = start;
costSoFar[start] = 0;
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
if (current.Equals(goal))
{
break;
}
foreach (var next in graph.Neighbors(current))
{
double newCost = costSoFar[current]
+ graph.Cost(current, next);
if (!costSoFar.ContainsKey(next)
|| newCost < costSoFar[next])
{
costSoFar[next] = newCost;
double priority = newCost + Heuristic(next, goal);
frontier.Enqueue(next, priority);
cameFrom[next] = current;
}
}
}
}
}
public class Test
{
static void DrawGrid(SquareGrid grid, AStarSearch astar) {
// Печать массива cameFrom
for (var y = 0; y < 10; y++)
{
for (var x = 0; x < 10; x++)
{
Location id = new Location(x, y);
Location ptr = id;
if (!astar.cameFrom.TryGetValue(id, out ptr))
{
ptr = id;
}
if (grid.walls.Contains(id)) { Console.Write("##"); }
else if (ptr.x == x+1) { Console.Write("u2192 "); }
else if (ptr.x == x-1) { Console.Write("u2190 "); }
else if (ptr.y == y+1) { Console.Write("u2193 "); }
else if (ptr.y == y-1) { Console.Write("u2191 "); }
else { Console.Write("* "); }
}
Console.WriteLine();
}
}
static void Main()
{
// Создание "рисунка 4" из предыдущей статьи
var grid = new SquareGrid(10, 10);
for (var x = 1; x < 4; x++)
{
for (var y = 7; y < 9; y++)
{
grid.walls.Add(new Location(x, y));
}
}
grid.forests = new HashSet<Location>
{
new Location(3, 4), new Location(3, 5),
new Location(4, 1), new Location(4, 2),
new Location(4, 3), new Location(4, 4),
new Location(4, 5), new Location(4, 6),
new Location(4, 7), new Location(4, 8),
new Location(5, 1), new Location(5, 2),
new Location(5, 3), new Location(5, 4),
new Location(5, 5), new Location(5, 6),
new Location(5, 7), new Location(5, 8),
new Location(6, 2), new Location(6, 3),
new Location(6, 4), new Location(6, 5),
new Location(6, 6), new Location(6, 7),
new Location(7, 3), new Location(7, 4),
new Location(7, 5)
};
// Выполнение A*
var astar = new AStarSearch(grid, new Location(1, 4),
new Location(8, 5));
DrawGrid(grid, astar);
}
}4 Оптимизации
При создании кода для статьи я делал упор на простоту и применимость, а не на производительность. Сначала заставь код работать, потом оптимизируй скорость. Многие оптимизации, использованные мной в реальных проектах, специфичны для проекта, поэтому вместо демонстрации оптимального кода я подскажу некоторые идеи, которые вы можете реализовать в собственном проекте:
4.1 Граф
Самая большая оптимизация, которую можно внести — уменьшение количества узлов. Рекомендация номер 1: если вы используете карту из сеток, то попробуйте применить граф поиска путей не на основе сеток. Это не всегда возможно, но такой вариант стоит рассмотреть.
Если граф имеет простую структуру (например, сетка), то вычисляйте соседей в функции. Если он имеет более сложную структуру (без сеток, или сетка большим количеством стен, как в лабиринте), то храните соседей в структуре данных.
Также можно сэкономить операции копирования на повторном использовании массива соседей. Вместо выполнения возврата каждый раз, выделите его один раз в коде поиска и передайте его в метод соседей графа.
4.2 Очередь
В поиске в ширину используется обычная очередь, а не очередь с приоритетами, применяемая в других алгоритмах. Очереди быстрее и проще, чем очереди с приоритетами. В других алгоритмах исследуется меньшее количество узлов. Для большинства игровых карт уменьшение количества исследуемых узлов стоит замедления других алгоритмов. Однако есть карты, в которых много не сэкономишь, и поэтому в них лучше использовать поиск в ширину.
Для очередей используйте вместо массива deque. deque обеспечивает возможность быстрой вставки и удаления с любой стороны, в то время как массив быстр только с одного конца. В Python стоит использовать collections.deque; в C++ рассмотрите контейнер deque. Однако для поиска в ширину даже не обязательно нужна очередь: в нём можно использовать два вектора, переключаясь между ними, когда один из них пуст.
Для очереди с приоритетами используйте двоичную кучу, а не массив или отсортированный массив. Двоичная куча обеспечивает возможность быстрой вставки и удаления, в то время как массив быстр только в чём-то одном. В Python рекомендую использовать heapq; в C++ попробуйте контейнер priority_queue.
В Python показанные мной выше классы Queue и PriorityQueue настолько просты, что можно встроить методы в алгоритм поиска. Не знаю, сможете ли вы много на этом выиграть, стоит потестировать. Версии C++ будут встроенными.
Заметьте, что в алгоритме Дейкстры приоритет очереди с приоритетами сохраняется дважды, один раз в очереди с приоритетами, второй — в cost_so_far, поэтому можно написать очередь с приоритетами, получающую приоритет из любого места. Не знаю, стоит ли оно того.
В стандартной реализации алгоритма Дейкстры используется изменения приоритета в очереди с приоритетами. Однако что произойдёт, если не менять приоритет? В результате там появятся дублирующие элементы. Но алгоритм всё равно работает. Он будет посещать повторно некоторые точки больше, чем нужно. В очереди с приоритетами будет больше элементов, чем необходимо, что замедляет работу, но структуры данных, поддерживающие изменение приоритета, тоже замедляют работу из-за наличия большего количества элементов. См. исследование «Очереди с приоритетами и алгоритм Дейкстры» Чена, Чаудхери, Рамачандрана, Лан-Роша и Тонга. Это исследование также рекомендует рассмотреть pairing heaps и другие структуры данных.
Если вы думаете над использованием чего-то вместо двоичной кучи, сначала измерьте размер границы и частоту изменения приоритетов. Профилируйте код и посмотрите, является ли очередь с приоритетами узким местом.
Я чувствую, что перспективным направлением является группирование данных. Также как блочная сортировка и поразрядная сортировка могут быть полезными альтернативами быстрой сортировки, когда ключами являются целочисленные значения, в случае с алгоритмов Дейкстры и A* ситуация даже ещё лучше. Приоритеты в алгоритме Дейкстры невероятно низки. Если самый нижний элемент в очереди имеет приоритет f, то самый верхний элемент имеет приоритет f+e, где e — максимальный вес ребра. В примере с лесом у нас есть веса рёбер 1 и 5. Это значит, что все приоритеты в очереди будут находиться между f и f+5. Поскольку все они являются целочисленными, всего есть шесть разных приоритетов. Можно использовать шесть блоков или вообще ничего не сортировать! В A* создаётся более широкий диапазон приоритетов, но всё равно этот способ стоит рассмотреть. И есть более интересные подходы к группировке, способные обрабатывать более широкий спектр ситуаций.
У меня есть ещё одна статья о структурах данных очередей с приоритетами.
4.3 Поиск
Эвристика увеличивает сложность и затраты времени ЦП. Однако целью здесь является исследование меньшего количества узлов. В некоторых картах (например, в лабиринтах), эвристика может и не добавлять много информации, и может быть лучше использовать более простой алгоритм без эвристики.
Если в вашем графе в качестве точек используются целочисленные значения, то рассмотрите возможность использования для cost_so_far, visited, came_from и т.д. простого массива, а не таблицы хешей. Поскольку visited является массивом boolean, можно использовать битовый вектор. Инициализируйте битовый вектор для всех идентификаторов, но оставьте cost_so_far и came_from неинициализированными (если язык это позволяет). Потом инициализируйте их только при первом посещении.
Если вы будете выполнять только один поиск за раз, то можно выделить статически и повторно использовать структуры данных из одного вызова в следующем. Вместо инициализации их на входе, выполняйте их сброс на выходе. Можно использовать массив для отслеживания изменяемых точек, а потом изменять только их. Например, если вы используете массив visited[], инициализированный под 1000 узлов, но большинство процессов поиска посещает меньше 100 узлов, то можно изменять массив индексов, а потом изменять только эти 100 узлов при выходе из функции, вместо повторной инициализации всех 1000 узлов при входе в функцию.
Некоторые люди используют для ускорения поиска A* недопустимую (переоценивающую) эвристику. Это кажется разумным. Однако я не рассматривал внимательно эти реализации. Полагаю (но не знаю точно), что некоторые уже посещённые элементы требуется посетить повторно, даже если они уже удалены из границы.
В некоторых реализациях в открытое множество всегда вставляется новый узел, даже если он уже там есть. Так можно избежать потенциально затратного этапа проверки того, находится ли уже узел в открытом множестве. Но при этом открытое множество становится больше/медленнее и в результате придётся оценивать больше узлов, чем необходимо. Если проверка открытого множества окажется затратной, то, возможно, стоит использовать такой подход. Однако в представленном мной коде я сделал проверку дешёвой, и не использую этот подход.
В некоторых реализациях не проверяется, лучше ли новый узел уже существующего в открытом множестве. Это позволяет избежать потенциально затратной проверки. Однако это может привести к ошибке. На некоторых типах карт вы не найдёте кратчайшего пути, если пропустите эту проверку. В представленном мной коде я выполняю эту проверку (new_cost < cost_so_far). Эта проверка дешевая, потому что я сделал поиск в cost_so_far дешёвым.
5 Устранение ошибок
5.1 Неверные пути
Если вы не получаете кратчайшего пути, попробуйте выполнить следующие проверки:
- Работает ли правильно очередь с приоритетами? Попробуйте остановить поиск и извлеките из очереди все элементы. Они должны идти по порядку.
- Переоценивает ли эвристика истинное расстояние?
priorityнового узла никогда не должен быть ниже приоритета его родителя, если вы не переоцениваете расстояние (это можно сделать, но вы больше не получите кратчайшего пути). - В языке со статической типизацией значения стоимости, эвристики и приоритетов должны иметь совместимые типы. Код примера в этой статье работает и с целочисленными типами, и с типами с плавающей запятой, но не все графы и эвристики ограничены целочисленными значениями. Поскольку приоритеты являются суммой стоимости и эвристики, то приоритеты должны иметь тип с плавающей запятой, если или стоимость, или эвристика имеют тип с плавающей запятой.
5.2 Некрасивые пути
Чаще всего при выполнении A* на сетках мне задают вопрос: почему пути не выглядят прямыми? Если сообщить A*, что все движения по сетке имеют равную стоимость, то получается множество кратчайших путей одной длины, и алгоритм произвольно выбирает один из них. Путь является кратким, но он не выглядит хорошим.
- Одним из решений будет спрямление путей после алгоритма с помощью алгоритма «string pulling».
- Ещё одно решение — направлять пути в нужную сторону регулированием эвристики. Есть несколько дешёвых трюков, которые работают не во всех ситуациях, здесь можно прочитать об этом подробнее.
- Третье решение — не использовать сетку. Сообщайте A* только места, в которых можно поворачивать, а не каждый квадрат сетки. Здесь можно прочитать об этом подробнее.
- Четвёртое решение — хак, но он работает не всегда. При итерации по соседям вместо использования одинакового порядка (например: север, восток, юг, запад), изменяйте порядок в «нечётных» узлах сетки (в которых (x+y) % 2 == 1). Я использую этот трюк в своих статьях.
6 Дополнительное чтение
- В учебниках алгоритмов часто используется математическая запись с однобуквенными именами переменных. В своих статьях я старался использовать более понятные имена переменных. Соответствия:
costиногда записывается как w or d или l или lengthcost_so_farобычно записывается как g или d или distanceheuristicобычно записывается как hpriorityв A* обычно записывается как f, где f = g + hcame_fromиногда записывается как π или parent или previous или prevfrontierобычно называется OPENvisited— это сопряжение OPEN и CLOSED- точки, например,
currentиnextзаписываются буквами u, v
- Ссылки на Википедию:
Автор: PatientZero



