Dropout — метод решения проблемы переобучения в нейронных сетях

в 11:38, , рубрики: big data, deep learning, dropout, neural networks, overfitting, wunder fund, wunderfund, Алгоритмы, Блог компании Wunder Fund, машинное обучение, метки:

Dropout — метод решения проблемы переобучения в нейронных сетях - 1

Переобучение (overfitting) — одна из проблем глубоких нейронных сетей (Deep Neural Networks, DNN), состоящая в следующем: модель хорошо объясняет только примеры из обучающей выборки, адаптируясь к обучающим примерам, вместо того чтобы учиться классифицировать примеры, не участвовавшие в обучении (теряя способность к обобщению). За последние годы было предложено множество решений проблемы переобучения, но одно из них превзошло все остальные, благодаря своей простоте и прекрасным практическим результатам; это решение — Dropout (в русскоязычных источниках — “метод прореживания”, “метод исключения” или просто “дропаут”).

Dropout

Dropout — метод решения проблемы переобучения в нейронных сетях - 2
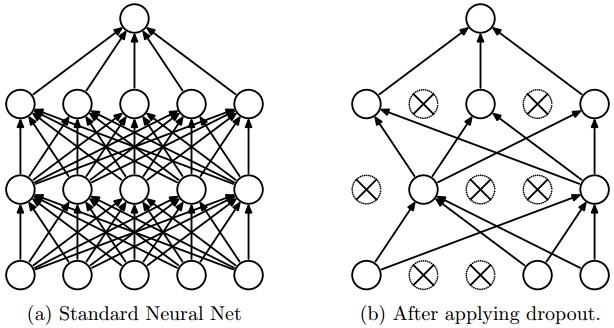
Графическое представление метода Dropout, взятое из статьи, в которой он впервые был представлен. Слева — нейронная сеть до того, как к ней применили Dropout, справа — та же сеть после Dropout.
Сеть, изображенная слева, используется при тестировании, после обучения параметрам.

Главная идея Dropout — вместо обучения одной DNN обучить ансамбль нескольких DNN, а затем усреднить полученные результаты.

Сети для обучения получаются с помощью исключения из сети (dropping out) нейронов с вероятностью $p$, таким образом, вероятность того, что нейрон останется в сети, составляет $q=1-p$. “Исключение” нейрона означает, что при любых входных данных или параметрах он возвращает 0.

Исключенные нейроны не вносят свой вклад в процесс обучения ни на одном из этапов алгоритма обратного распространения ошибки (backpropagation); поэтому исключение хотя бы одного из нейронов равносильно обучению новой нейронной сети.

Цитируя авторов,

В стандартной нейронной сети производная, полученная каждым параметром, сообщает ему, как он должен измениться, чтобы, учитывая деятельность остальных блоков, минимизировать функцию конечных потерь. Поэтому блоки могут меняться, исправляя при этом ошибки других блоков. Это может привести к чрезмерной совместной адаптации (co-adaptation), что, в свою очередь, приводит к переобучению, поскольку эти совместные адаптации невозможно обобщить на данные, не участвовавшие в обучении. Мы выдвигаем гипотезу, что Dropout предотвращает совместную адаптацию для каждого скрытого блока, делая присутствие других скрытых блоков ненадежным. Поэтому скрытый блок не может полагаться на другие блоки в исправлении собственных ошибок.

В двух словах, Dropout хорошо работает на практике, потому что предотвращает взаимоадаптацию нейронов на этапе обучения.

Получив приблизительное представление о методе Dropout, давайте рассмотрим его подробнее.

Как работает Dropout

Как уже говорилось, Dropout выключает нейроны с вероятностью $p$ и, как следствие, оставляет их включенными с вероятностью $q=1-p$.

Вероятность выключения каждого нейрона одинакова. Это означает следующее:

При условии, что

  • $h(x)=xW + b$ — линейная проекция входного $d_i$-мерного вектора x на $d_h$-мерное пространство выходных значений;
  • $a(h)$ – функция активации,

применение Dropout к данной проекции на этапе обучения можно представить как измененную функцию активации:

$f(h)=D⊙a(h),$

где $D=(X_1,⋯,X_{d_h})$ – $d_h$-мерный вектор случайных величин $X_i$, распределенных по закону Бернулли.

$X_i$ имеет следующее распределение вероятностей:

$$display$$f(k;p)=begin{equation*}begin{cases}p, &mathrm{if}& k=1\1-p,&mathrm{if}& k=0end{cases}end{equation*},$$display$$

где $k$ — все возможные выходные значения.

Очевидно, что эта случайная величина идеально соответствует Dropout, примененному к одному нейрону. Действительно, нейрон выключают с вероятностью $p=P(k=1)$, в противном случае — оставляют включенным.

Посмотрим на применение Dropout к i-му нейрону:

$$display$$O_i=X_ia(sum_{k=1}^{d_i}{w_kx_k+b})=begin{equation*}begin{cases}a(sum_{k=1}^{d_i}{w_kx_k+b}), &mathrm{if}& X_i=1\0,&mathrm{if}& X_i=0end{cases}end{equation*},$$display$$

где $P(X_i=0)=p$.

Так как на этапе обучения нейрон остается в сети (не подвергается выключению) с вероятностью q, на этапе тестирования нам необходимо эмулировать поведение ансамбля нейронных сетей, использованного при обучении. Для этого авторы предлагают на этапе тестирования умножить функцию активации на коэффициент q. Таким образом,

На этапе обучения:$O_i=X_ia(sum_{k=1}^{d_i}{w_kx_k+b})$,

На этапе тестирования:$O_i=qa(sum_{k=1}^{d_i}{w_kx_k+b})$

Обратный (Inverted) Dropout

Возможно использовать немного другой подход — обратный Dropout. В данном случае мы умножаем функцию активации на коэффициент не во время тестового этапа, а во время обучения.

Коэффициент равен обратной величине вероятности того, что нейрон останется в сети: $frac{1}{1-p}=frac{1}{q} $, таким образом,

На этапе обучения: $O_i=frac{1}{q}X_ia(sum_{k=1}^{d_i}{w_kx_k+b})$,
На этапе тестирования: $O_i=a(sum_{k=1}^{d_i}{w_kx_k+b})$

Во многих фреймворках для глубокого обучения Dropout реализован как раз в этой модификации, так как при этом необходимо лишь однажды описать модель, а потом запускать обучение и тестирование на этой модели, меняя только параметр (коэффициент Dropout).

В случае прямого Dropout мы вынуждены изменять нейронную сеть для проведения тестирования, так как без умножения на q нейрон будет возвращать значения выше, чем те, которые ожидают получить последующие нейроны; именно поэтому реализация обратного Dropout встречается чаще.

Dropout множества нейронов

Легко заметить, что слой $h$ из $n$ нейронов на отдельном шаге этапа обучения можно рассматривать как ансамбль из $n$ экспериментов Бернулли с вероятностью успеха $p$.

Таким образом, на выходе слоя $h$ мы получаем следующее количество исключенных нейронов:

$Y=sum_{i=1}^{d_h}(1-X_i)$

Так как каждый нейрон представлен в виде случайной величины, распределенной по закону Бернулли, и все эти величины независимы, общее число исключенных нейронов — также случайная величина, но имеющая биномиальное распределение:

$Y∼Bi(d_h, p),$

где вероятность $k$ успешных событий за $n$ попыток характеризуется следующей плотностью распределения:

$f(k; n,p)=begin{pmatrix}n\kend{pmatrix}p^k(1-p)^{n-k}$

Эту формулу легко объяснить следующим образом:

  • $p^k(1-p)^{n-k} $ — вероятность получения последовательности $k$ успешных событий за $n$ попыток, и, следовательно, $n-k$ неуспешных.
  • $begin{pmatrix}n\kend{pmatrix}$ — биномиальный коэффициент, используемый для расчета количества возможных успешных последовательностей.

Теперь мы можем использовать это распределение, чтобы рассчитать вероятность отключения определенного количества нейронов.

Используя метод Dropout, мы фиксируем коэффициент Dropout $p$ для определенного слоя и ожидаем, что из этого слоя будет исключено пропорциональное количество нейронов.

Например, если слой, к которому мы применили Dropout, состоит из $n=1024$ нейронов, а $p=0.5$, мы ожидаем, что 512 из них будет отключено. Давайте проверим это утверждение:

$Y=sum_{i=1}^{1024}X_i∼Bi(1024,0.5)$

$P(Y=512)=begin{pmatrix}1024\512end{pmatrix}0.5^{512}(1-0.5)^{1024-512}approx0.025$

Как видим, вероятность отключения ровно $np=512$ нейронов составляет всего 0.025!

Следующий скрипт на Python 3 поможет представить, сколько нейронов будет выключено для разных значений $p$ и зафиксированного количества $n$.

import matplotlib.pyplot as plt
from scipy.stats import binom
import numpy as np

# number of neurons
n = 1024
# number of tests (input examples)
size = 500
# histogram bin width, for data visualization
binwidth = 5

for p in range(1, 10):
    # per layer probability
    prob = p / 10
    # generate size values from a bi(n, prob)
    rnd_values = binom.rvs(n, prob, size=size)
    # draw histogram of rnd values
    plt.hist(
        rnd_values,
        bins=[x for x in range(0, n, binwidth)],
        # normalize = extract the probabilities
        normed=1,
        # pick a random color
        color=np.random.rand(3, 1),
        # label the histogram with its probability
        label=str(prob))

plt.legend(loc='upper right')
plt.show()

Dropout — метод решения проблемы переобучения в нейронных сетях - 47
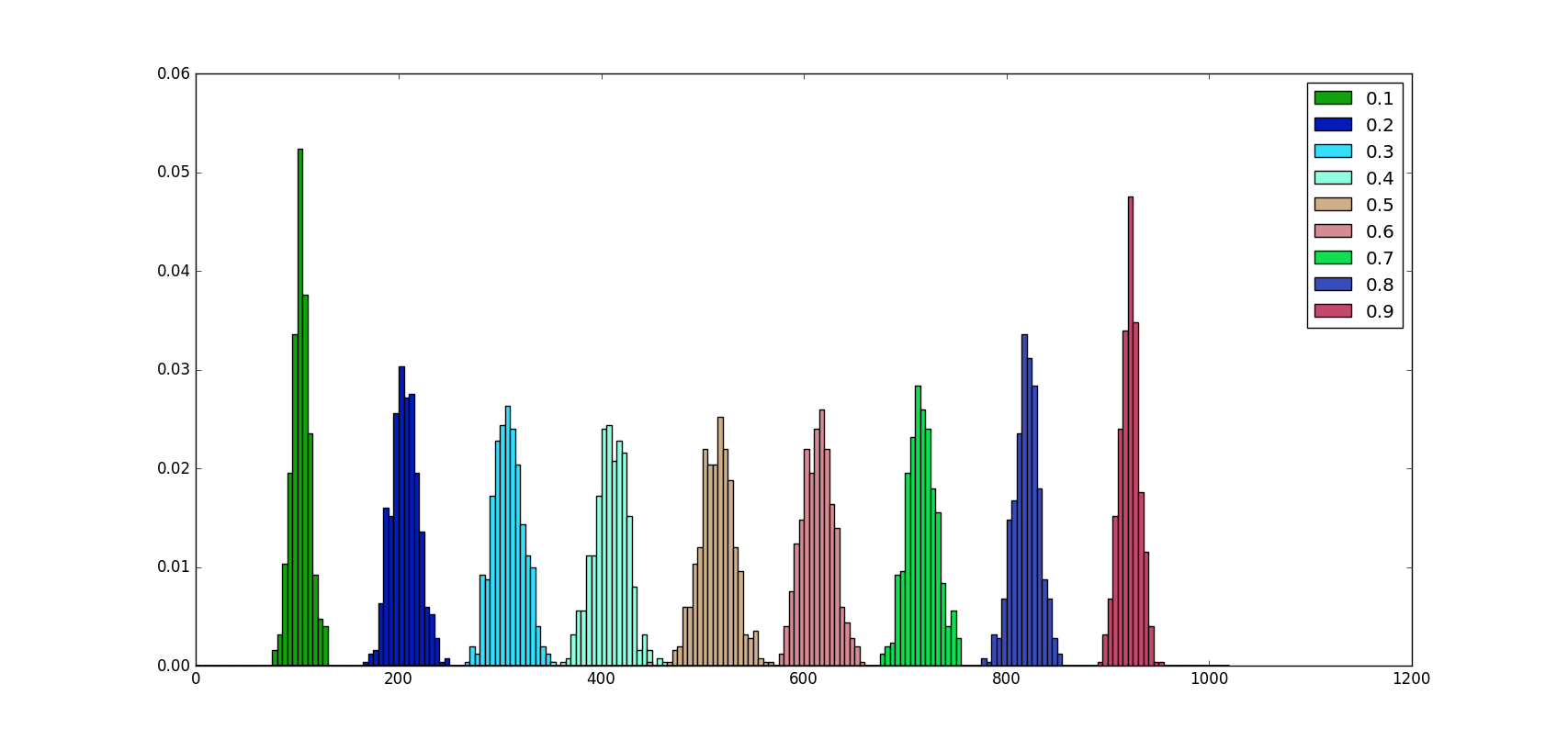
Биномиальное распределение достигает максимума в районе $np$

Как видим из изображения выше, для любого $p$ среднее количество выключенных нейронов пропорционально $np$, то есть

$E[Bi(n,p)]=np$

Более того, можно заметить, что распределение значений почти симметрично относительно $p=0.5$ и вероятность выключения $np$ нейронов возрастает по мере того, как увеличивается расстояние от $p=0.5$.

Коэффициент масштабирования введен авторами для компенсации значений активации, так как на этапе обучения используется лишь доля от $1-p$ нейронов, в то время как на этапе тестирования все 100% нейронов остаются включенными, и, следовательно, полученные значения необходимо уменьшить с помощью специального коэффициента.

Dropout и другие регуляризаторы

Dropout часто используется с L2-нормализацией и другими методами ограничения параметров (например, Max Norm). Методы нормализации помогают поддерживать невысокие значения параметров модели.

Вкратце, L2-нормализация представляет собой дополнительный элемент функции потерь, где $lambdain[0,1]$ — гиперпараметр, называемый “сила регуляризации” (regularization strength), $F(W;x)$ — модель, а $epsilon$ — функция ошибки между реальным значением $y$ и предсказанным $hat{y}$:

$mathcal{L}(y,hat{y})=epsilon(y,F(W;x))+frac{lambda}{2}W^2$

Нетрудно понять, что этот дополнительный элемент сокращает величину, на которую изменяется параметр во время обратного распространения ошибки методом градиентного спуска. Если $eta$ — коэффициент скорости обучения, то параметр $win{W}$ обновляется на следующую величину:

$wleftarrow{w-eta(frac{partial F(W;x)}{partial w}+lambda w)} $

Dropout сам по себе не может предотвратить рост значений параметров на этапе обновления. Более того, обратный Dropout ведет к тому, чтобы шаги обновления стали даже больше, как показано ниже.

Обратный Dropout и другие регуляризаторы

Так как Dropout не предотвращает роста параметров и их переполнения, нам может помочь L2-регуляризация (или любой другой метод регуляризации, ограничивающий значения параметров).

Если мы представим коэффициент Dropout в явном виде, уравнение выше превратится в следующее:

$wleftarrow{w-eta(frac{1}{q}frac{partial F(W;x)}{partial w}+lambda w)} $

Нетрудно заметить, что в случае обратного Dropout скорость обучения масштабируется с помощью коэффициента $q$. Так как $q$ принадлежит интервалу $[0;1]$, отношение между $eta$ и $q$ может принимать значения из следующего интервала:

$r(q)=frac{eta}{q}in [eta=lim_{q rightarrow 1}r(q), +infty=lim_{q rightarrow 0}r(q)]$

Поэтому отныне мы будем называть $q$ ускоряющим множителем (boosting factor), так как он увеличивает скорость обучения. $r(q)$ будем называть эффективной скоростью обучения (effective learning rate).

Эффективная скорость обучения выше, чем скорость обучения, выбранная нами: таким образом метода нормализации, ограничивающие значения параметров, могут упростить процесс выбора скорости обучения.

Итоги

  1. Dropout существует в двух модификациях: прямой (используется нечасто) и обратный.
  2. Dropout на отдельном нейроне может быть представлен как случайная величина с распределением Бернулли.
  3. Dropout на множестве нейронов может быть представлен как случайная величина с биномиальным распределением.
  4. Несмотря на то, что вероятность того, что из сети будет выключено ровно np нейронов, np — среднее количество нейронов, отключенных в слое из n нейронов.
  5. Обратный Dropout увеличивает скорость обучения.
  6. Обратный Dropout следует использовать совместно с другими методами нормализации, ограничивающими значения параметров, чтобы упростить процесс выбора скорости обучения.
  7. Dropout помогает предотвратить проблему обучения в глубоких нейронных сетях.
О, а приходите к нам работать? :)

wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.

Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.

Присоединяйтесь к нашей команде: wunderfund.io

Автор: wunder_editor

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js