Алгоритм ACOR
Привет, хабра. Хочу поделиться имеющийся у меня информацией по методам оптимизации, а именно по оптимизации методом колонии муравьев. В данной статье представлен алгоритм ACOR (Ant Colony Optimization for continuous domain). В будущем планирую представить еще несколько алгоритмов колонии муравьев. Может быть кому-нибудь пригодиться в университете или по работе.
Постановка задачи
Рассматриваем решение детерминированной задачи оптимизации. Детерминированная задача оптимального решения формулируется следующим образом
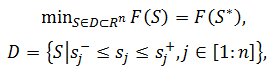
где R^n – n-мерное пространство, D – область допустимых значений вектора варьируемых параметров, S – n-мерный вектор варьируемых параметров, S* – оптимальное значение вектора варьируемых параметров, F(S) – целевая функция (критерий оптимальности), F(S*) – оптимальное значение критерия оптимальности.
Общие сведения
Алгоритм ACOR (Ant Colony Optimization for continuous domain) успешно заменяет дискретный алгоритм ACO без необходимости вносить какие-либо изменения в его схему. Другие алгоритмы непрерывной оптимизации хоть и основаны на алгоритме ACO (continuous-ACO, API, алгоритм непрерывно взаимодействующих колоний муравьев (CIAC)), но в большинстве своем не повторяют его схему.
Основная идея ACOR – приращение компонентов вектора варьируемых параметров, полученного на зависимом (от феромонов) вероятностном выборе компонентов. Это достигается путем замены дискретного распределения вероятностей непрерывной функцией, называемой функцией плотности вероятностей (Probability Density Function (PDF)), так же известной как распределение Гаусса.
Алгоритм ACOR использует «ядро» Гаусса (Gaussian Kernel) для взвешенного суммирования нескольких функций плотности вероятности. «Ядро» Гаусса – G^i(S) определяется по формуле
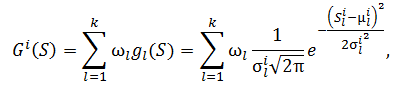
где k – число функций плотности вероятности, i – измерение, ωl – весовая функция, μl^i – вектор средних значений (вектор математических ожиданий), σl^i – вектор дисперсий.
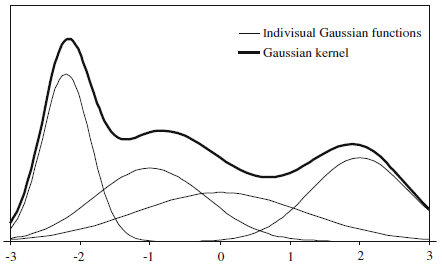
Рисунок 1 – Пример «ядра» Гаусса, состоящего из четырех функций Гаусса
Модель феромонов ACOR определяется ранжирования архива решений T. На каждой итерации, полученный набор решений добавляется в архив решений T и упорядочивается по критерию оптимальности. В архиве решений T всегда находится k решений, в результате чего на каждой итерации множество худших решений должны быть удалены. Это процедура имитирует процесс обновления феромонов в дискретных алгоритмах ACO. Цель этого процесса состоит в том, чтобы смещать процесс поиска в сторону лучших решений, найденных при оптимизации.
Схема алгоритма
Для удобного представления решений используют массив решений, представленный в таблице 1. В таблице решений, решения хранятся согласно их рангу (s1^i– лучшее), ωl – вес каждой функции плотности вероятности, ω1≥ω2≥⋯≥ωn, «ядро» Гаусса для i-го шага – G^i (S), которое вычисляется, используя только i-ый компонент всех k решений в архиве T.
Таблица 1 – Таблица решений
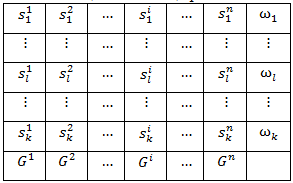
Для получения решения, муравей на каждом шаге i=1,…,n, выбирает значение решения S^i в n-мерной задачи оптимизации.
1) Для k-муравьев случайным образом получают решения s^1,…,s^n.
2) Упорядочивают значения целевой функции, где ранг решения l=1 является лучшим.
3) Вычисляют вес ωl для каждого решения
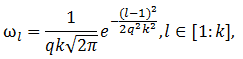
где q – коэффициент. При фиксированном k, малое значение q (~ 0) означает, что только функция плотности вероятности лучшего решения будет использована для создания нового решения, в то время как при большом значении q, получается более равномерная вероятность. При большом значении q, уменьшается скорость получения конечного результата.
4) Вычисляют вероятность каждого решения
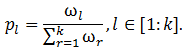
5) Методом рулетки, случайно выбирают одно решение – Sl, используя рассчитанную вероятность.
6) Полагают, что математическое ожидание μl^i равно sl^i.
7) Вычисляют дисперсию (отклонение от sl^i) в i-ом измерении по формуле
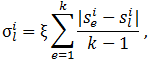
где i∈[1:n], а ξ – коэффициент, который определяет испарение феромонов (ξ>0).
8) Получают решение, используя генератор случайных чисел и распределение вероятностей, полученных с помощью «ядра» Гаусса.
9) Вычисляют значений целевой функции каждого решения.
10) Добавляют полученные решения в архив решений T.
11) Упорядочивают полученные решения.
12) Сохраняют k решения в архиве T.
13) Если лучшее решение удовлетворяет критериям поиска, завершают поиск, иначе переходят на третий шаг.
Список использованных источников
1. Mohamad M., Tokhi M., Omar O. M. Continuous Ant Colony Optimization for Active Vibration Control of Flexible Beam Structures // IEEE International Conference on Mechatronics (ICM). Apr., 2011, — P. 803-808.
2. Madadgar S., Afshar A. An Improved Continuous Ant Algorithm for Optimization of Water Resources Problem // Water Resources Management. -2009. — Vol. 23. — NO. 10. – P. 2119-2139.
Автор: Pashk88