(Прим. пер.: приведённые в статье алгоритмы относятся к названиям степеней тысячи по короткой шкале.)
Некоторое время назад я получил возможность поучаствовать в разработке игры в жанре idle. Что же такое idle-игра? Если вы впервые слышите об этом быстро развивающемся жанре, попробуйте поиграть в Adventure Capitalist. На сайте Gamasutra также есть несколько статей (1, 2, 3, 4), позволяющих рассмотреть жанр немного глубже.
Одна из проблем, с которой разработчик idle-игры неизбежно столкнётся, — как разместить все эти огромные числа на экране, и, что более важно — как игроку разобраться в них. В этой статье мы посмотрим, как можно переписать очень длинные числа как строки, которые будут удобны для игроков. Можно разбить этот процесс на две основные части:
- Во-первых, мы представим число в экспоненциальной записи. Некоторые разработчики игр жанра idle останавливаются на этом, и похоже, части игроков это нравится. В Wolfram MathWorld есть очень прямолинейный алгоритм для перевода числа, его мы и будем использовать. Но есть и другой подход, который можно применять, если вы предпочитаете поиграться с битами. Я просто упоминаю его, мы не будем рассматривать его в этой статье. Если вы хотите использовать его в своей игре, взгляните на папку загрузки этой статьи, в которой есть простой в использовании скрипт экспоненциальной записи:
ScientificNotation.FromDouble(12340000); // .significand == 1.234; .exponent == 7 - Найдя представление числа в экспоненциальной записи, мы можем подобрать название для его порядка. Это и будет главной задачей этой статьи.
Скачивание исходного кода
Исходный код доступен для скачивания и готов к использованию в ваших idle-играх. Использовать его просто:
LargeNumber.ToString (12340000); // результатом будет "12.34 million"
Также в файлы загрузки включён небольшой пример программы, демонстрирующий, насколько большие числа конвертируются в игре в строки (с помощью скриптов кнопок, описанных в предыдущей статье):
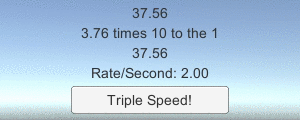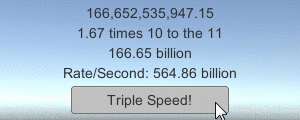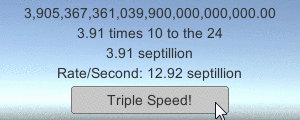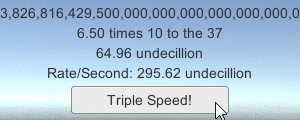
Всё это часть набора примеров кода, который должен сопровождать некоторые мои статьи, написанные ранее, в основном из туториалов по работе с сетью в Unity (1, 2, 3). Скачивайте примеры кода, чтобы проверить, как они работают!
Строки стандартного числового формата
Числа меньше миллиона достаточно малы и не требуют серьёзной обработки. Можно положиться на встроенные возможности форматирования чисел C#, они сделают за нас бóльшую часть работы:
double x = 987654.321
x.ToString ("N2"); // возвращает "987,654.32"
Добавляя соответствующий аргумент к методу ToString, мы почти без труда группируем разделители и ограниченные десятичные разряды. Нам не нужно выполнять дополнительное деление или использовать функции округления вниз.
Латинские префиксы к не очень большим числам
При работе с большими числами, выражающимися в миллионах (millions), биллионах (billions), триллионах (trillions) и так далее, мы знаем, что названия меняются через каждые три разряда. Имея число в экспоненциальной записи, мы знаем, что оно выражается в миллионах, если его порядок от 6 до 8, в биллионах — от 9 до 11, и в триллионах, если показатель от 12 до 14, и т.д. В общем виде для числа с экспоненциальной записью:
M x 10N
Нам нужно выразить N следующим образом:
N = 3(U+1) + V, где V < 3
Тогда конечной строкой числа будет:
M*(10^V) Name(U)+"llion"
где Name(U) можно получить из этой таблицы латинских префиксов:
| U | Name(U) |
| 1 | mi |
| 2 | bi |
| 3 | tri |
| 4 | quadri |
| 5 | quinti |
| 6 | sexti |
| 7 | septi |
| 8 | octi |
| 9 | noni |
Например, если мы обрабатываем число 123 000 000 000 000 000, можно выразить его в экспоненциальной записи так:
1.23 x 1017, откуда M = 1.23 и N = 17
Переписывая N, мы получаем:
17 = 3*(4+1) + 2, откуда U = 4 и V = 2
Это значит, что наше число выглядит как:
1.23*(102) Name(4)+"llion"
Упрощая, получаем:
123 quadrillion
Сочетания префиксов для больших чисел
В Википедии есть полезная статья, объясняющая, как даются названия большим числам. Я не буду повторять то, что там написано. Вместо этого я дам описание того, как можно подойти к алгоритму и представлю несколько примеров.
Получив значение U числа (прим. пер.: здесь и далее у автора написано N, но это явно неправильно), как мы делали это в числах с латинскими префиксами, нужно разбить его на разряды (единицы, десятки, сотни), а затем сформулировать название следующим образом:
(префикс единиц) + (модификатор) + (префикс десяток) + (префикс сотен) + (удаление "a" в конце) + "llion"
Префиксы единиц, десяток и сотен можно взять из таблицы в статье Википедии. В некоторых случаях необходимо добавить модификатор, если кроме определённых префиксов единиц мы ставим префиксы десяток или сотен, но в большинстве случаев модификатор не нужен. Давайте рассмотрим несколько примеров.
Если U = 12, то для единиц цифра будет равна 2, что соответствует «duo», а для десятков — 1, соответствующая «deci». При переходе от «duo» к «deci» модификатор не нужен. По приведённой выше формуле мы получаем «duodecillion».
Если U = 27, для единиц цифра равна 7 (соответствует «septe»), для десятков — 2 (соответствует «viginti»). Согласно таблице, переход от «septe» к «viginti» требует модификатора «m». Соединяя всё вместе, получаем «septemvigintillion».
И наконец, если U = 30, то цифра для десятков равна 3, что соответствует «triginta», которое имеет окончание «a». Поэтому мы отбрасываем её и получаем «trigintillion».
Если вы пытаетесь понять, как всё это будет выглядеть в коде, то отвечу: это будет сочетание поисков по массиву, нескольких конструкций if и операций конкатенации и подстановки строк. Если вам повезло и вы работаете с языком, поддерживающим сравнения с паттернами, то можно использовать их.
Файлы исходного кода содержат работающую реализацию, обрабатывающую все случаи до U = 999. Она была протестирована на всех названиях, включённых в список больших чисел. Я призываю вас скачать их, если вам нужен готовый к использованию код, который можно легко вставить в собственные проекты, или если вы хотите сравнить свою реализацию с работающей версией.
А если U = 1000?
Тогда число называется миллиллионом (прим. пер.: в длинной шкале — квингентиллиардом).
Большие числа недостаточно велики
Числа двойной точности с плавающей запятой позволяют работать с числами до 10308, или U=101. Если в вашей игре требуются числа большей величины, то можно попробовать хранить числа с произвольной точностью. Таким образом можно сделать игроков миллиллионерами.
Но прежде спросите себя, действительно ли вам это нужно. Бесконечность предоставляет нам достаточно простора для разработки игр, и нам не обязательно пытаться заполнить всё данное нам пространство. Перефразирую моего профессора из колледжа: «Подумайте о самом большом конечном числе, которое можете придумать. Теперь используйте то же число как его же показатель степени, и возведите это число в степень самого себя. Если теперь расположить это число на оси действительных чисел, то по сравнению с бесконечностью оно всё равно будет очень близко к нулю».
Станет ли ваша игра интереснее от выхода за пределы чисел двойной точности? Для некоторых игр ответ может быть положительным, но в большинстве случаев я советую вам подумать ещё раз о балансе и дизайне игры (1, 2, 3, 4).
Если вам понравилась статья, не забудьте скачать папку с проектом! Надеюсь, она будет полезна при разработке вашей собственной игры. Спасибо за прочтение!
Автор: PatientZero






