Диаграммы разложения на простые множители

Недавно в свободное время написал программу для генерации диаграмм, полученных с помощью разложения числа на простые множители или "факторизационных диаграмм".

Вот так выглядит 700:

По расположению точек несложно заметить, что всего их здесь 7*5*5*2*2.

Далее описание того, как это работает.

Для начала несколько импортов: функция для разложения целого числа на простые множители и библиотека для отрисовки диаграмм.

module Factorization where

import Math.NumberTheory.Primes.Factorisation (factorise)

import Diagrams.Prelude
import Diagrams.Backend.Cairo.CmdLine

type Picture = Diagram Cairo R2

Функция primeLayout принимает целое число n (должно быть простым числом) и какое-то изображение, и затем симметрично располагает n копий изображения.

primeLayout :: Integer -> Picture -> Picture 

Для 2 есть особый случай: если изображение по ширине больше, чем по высоте, то две копии рисуются одна над другой, иначе они рисуются рядом. В обоих случаях мы добавляем небольшое пространство между копиями (равное половине высоты или ширины соответственно).

primeLayout 2 d
  | width d > height d = d === strutY (height d / 2) === d
  | otherwise          = d ||| strutX (width d / 2)  ||| d

Это значит, что если есть несколько коэффициентов, равных двум, и мы вызываем primeLayout несколько раз, получается что-то вроде:

Если бы мы всегда рисовали копии рядом друг с другом, мы бы получили

что не так красиво и наглядно.

Для других чисел, мы создаем правильный многоугольник соответствующего размера и распологаем копии по вершинам многоугольника.

primeLayout p d = decoratePath pts (repeat d)
  where pts = polygon with { polyType   = PolyRegular (fromIntegral p) r
                           , polyOrient = OrientH
                           }
        w = max (width d) (height d)
        r = w * c / sin (tau / (2 * fromIntegral p))
        c = 0.75

Например, вот primeLayout 5, примененная к зеленому квадрату:

Далее, имея список простых множителей, мы рекурсивно создаем все изображение.
Если список пуст, это соответствует цифре 1, поэтому мы просто рисуем черную точку.

factorDiagram' :: [Integer] -> Diagram Cairo R2
factorDiagram' []     = circle 1 # fc black

В ином случае если первое простое число называется p, а остальные ps, мы рекурсивно создаем изображение из остальных простых чисел ps и рисуем p копий этого изображения используя функцию primeLayout.

factorDiagram' (p:ps) = primeLayout p (factorDiagram' ps) # centerXY

И наконец, чтобы превратить число в факторизационную диаграмму, мы раскладываем его на простые множители, нормализуем их в список простых чисел, переворачиваем, чтобы большие числа были в начале и вызываем factorDiagram'.

factorDiagram :: Integer -> Diagram Cairo R2
factorDiagram = factorDiagram' 
              . reverse 
              . concatMap (uncurry $ flip replicate) 
              . factorise

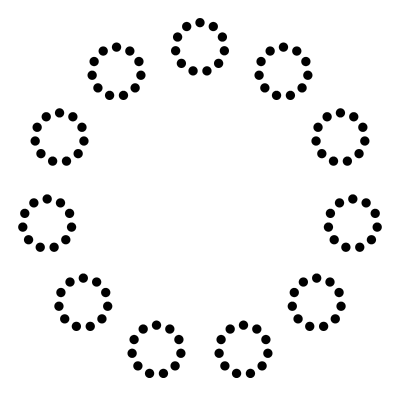
И вуаля! Разумеется, это хорошо работает лишь с числами из диапазона {2, 3, 5, 7} (и возможно 11). Например, вот так выглядит 121:

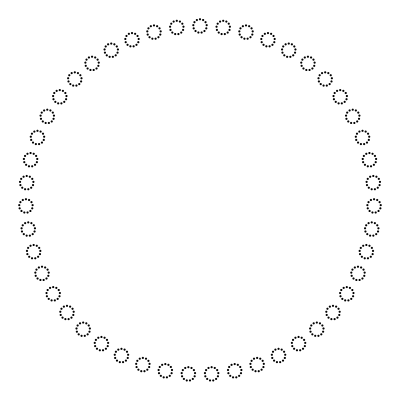
А так 611:

Тут диаграммы всех целых чисел от 1 до 36:

Степени тройки особенно интересны, так как их диаграммы это треугольники Серпинского. Вот, например, 3⁵ = 243:

Степени двойки тоже весьма неплохи, они представляют собой фракталы, называемые Канторова пыль. Вот 2¹⁰ = 1024:

И напоследок 104:

P.S.: Практического применения особо нет (разве что для демонстрации разложения числа на простые множители), но выглядит забавно. :)
В конце оригинальной статьи автор говорит, что хотел бы оформить приложение в виде сайта, чтобы любой мог ввести свое число и посмотреть результат.
Я сделал нечто подобное на javascript, желающие могут поэксперементировать тут. Производительность ниже, чем у haskell версии, поэтому аккуратнее с большими числами.
P.P.S.: Пост из песочницы, поэтому заранее извиняюсь, что не оформил перевод подобающим образом.

Автор: helarqjsc