Некоторое время назад (о, боже, уже год прошёл!) на вопрос, будет ли кому-то интересен обзор по современным методам сегментации изображения страницы документа, я получил положительный ответ (от massimus). И сегодня наконец-то решил этот обзор сделать.
Но для начала – маленькое отступление. Систему распознавания текста в наших продуктах можно описать очень просто. У нас есть страница с текстом, мы разбираем ее на текстовые блоки, затем блоки разбираем на отдельные строчки, строчки на слова, слова на буквы, буквы распознаем, дальше по цепочке собираем все обратно в текст страницы. Задача сегментации ставится примерно так: есть страница, надо её декомпозировать на текстовые и нетекстовые элементы.
Дальше задачу можно уточнять и уточнять (здесь я уже вам поднадоел с разъяснениями, что правильная формулировка задачи — уже полшага к её решению; можете не сомневаться, коллег и начальство я достал этим ещё сильнее). Научные работники из разных стран, авторы приводимых методов, хотят заниматься наукой, а не казуистикой, поэтому формулируют свою задачу попроще:
На странице есть текст и картинки. Требуется разбить на блоки текст и выделить картинки.
Источником вдохновения для меня послужила статья F. Shafait, D. Keysers, and Th. Breuel. Performance Comparison of Six Algorithms for Page Segmentation (далее я буду её называть SKB, по начальным буквам фамилий авторов), где дана сравнительная оценка практически всех приведённых методов сегментации. Так что если хотите сразу покопаться в первоисточниках — то лучше брать её и идти по ссылкам. А описание самих алгоритмов, подробности и обсуждение — здесь.
Итак, нам нужно разбить текст на блоки и выделить картинки. Как видите, о таблицах, диаграммах и прочих изысках здесь речи не идёт; более того, часто предполагают, что картинки высококонтрастны и при этом хорошо бинаризованы — то есть их границы в принципе можно найти, работая только с монохромным изображением.
Также в исследованиях часто используют понятия «манхеттенский» и «неманхеттенский» layout. «Манхеттенский» — это такой, в котором границы всех блоков прямые (каждый блок или прямоугольный, или представляет собой несколько прямоугольников, у которых некоторые вершины и части сторон общие), «неманхеттенский» не удовлетворяет таким ограничениям.
Для начала мы разберём некоторые алгоритмы, предназначенные для работы с «манхеттенским» документом.
Smearing
Это наиболее древний алгоритм — пожалуй, первое, что приходит в голову, когда сталкиваешься с задачей сегментации. Впервые описан в далёком 1982 году, в статье K. Y. Wong, R. G. Casey, F. M. Wahl. Document Analysis System.
В двух словах он работает так: давайте немножко размажем слова по вертикали и по горизонтали, получившиеся связные области будут готовыми блоками.
Если описать чуть подробнее, то получится так:
- Берём изображение страницы в RLE-представлении
- Удаляем белые RLE-штрихи (= последовательность белых пикселов) длиной меньше lT_horz. Получаем изображение Image_1
- Исходное изображение поворачиваем на 90 градусов и на повёрнутом изображении удаляем белые RLE-штрихи длиной меньше lT_vert. Поворачиваем изображение обратно и получаем изображение Image_2
- Делаем AND изображений Image_1 и Image_2
- На полученном изображении ещё разик удалим белые штрихи длиной меньше T_Final
Связанные области на полученном изображении — это готовые блоки. Их стоит разделить на текстовые и нетекстовые. В 1982 году ещё не было такого арсенала средств машинного обучения, без них было трудно — дерево решений рисовали вручную.
Вот так примерно выглядят промежуточные изображения и конечные блоки:
В оригинальной статье авторы работали с картинкой с разрешением 240 dpi и подобрали значения T_horz = 300 T_vert = 500 и T_final = 30. Несколько неожиданно, что значения получились столь большими (T_vert аж два дюйма с гаком), видимо это связано с тем, что делается AND.
Преимущества алгоритма понятны — он прост, работает с RLE изображением и только с ним, а значит и быстр. Сам алгоритм нигде явно не опирается на то, что входной документ — «манхеттенский». Впрочем, если подумать, то на «неманхеттенском» алгоритм не сработает — на приведённом ниже примере текст приклеится к картинке.
По-настоящему плохая новость состоит в том, что на «манхеттенском» документе склейки текста и «нетекста» также очень часты, в SKB это подмечено.
Recursive XY cut
Через пару лет, в 1984 году, был описан более продвинутый метод сегментации страницы, который называется recursive XY cut. Он описан в статье G. Nagy and S. Seth. «Hierarchical representation of optically scanned documents» и в 90-е годы активно развивался.
Про этот метод уже явным образом сказано, что он годится только для манхеттенского документа. Суть метода в том, что мы разбиваем страницу на блоки попеременно, деля блоки по вертикали или по горизонтали. То есть алгоритм примерно такой:
- Готовим страницу, очищая её от мелкого мусора
- Выделяем связные области. Можно даже и немного их пообъединять и получить что-то вроде слов, если вдруг кто-то умеет такие объединения безопасно строить. Но в рамках данного поста будем называть их “связные области”.
- Вычисляем глобальные параметры алгоритма, к примеру, медианную высоту и ширину символа.
Далее алгоритм запускаем рекурсивно, начиная со всей страницы:
- Ищем, как бы можно поделить блок вертикальным или горизонтальным разрезом.
- Если смогли — делим и рекурсивно запускаем деление каждой из частей.
- Если не смогли, останавливаемся.
Что касается пункта о том, как делить блок. Предлагается два способа — или по белому просвету (его можно найти на проекции блока на горизонтальную или вертикальную ось соответственно) или по длинной и достаточно хорошо изолированной чёрной прямой линии.
В результате всех этих делений получается древесная структура, как справа внизу на рисунке:
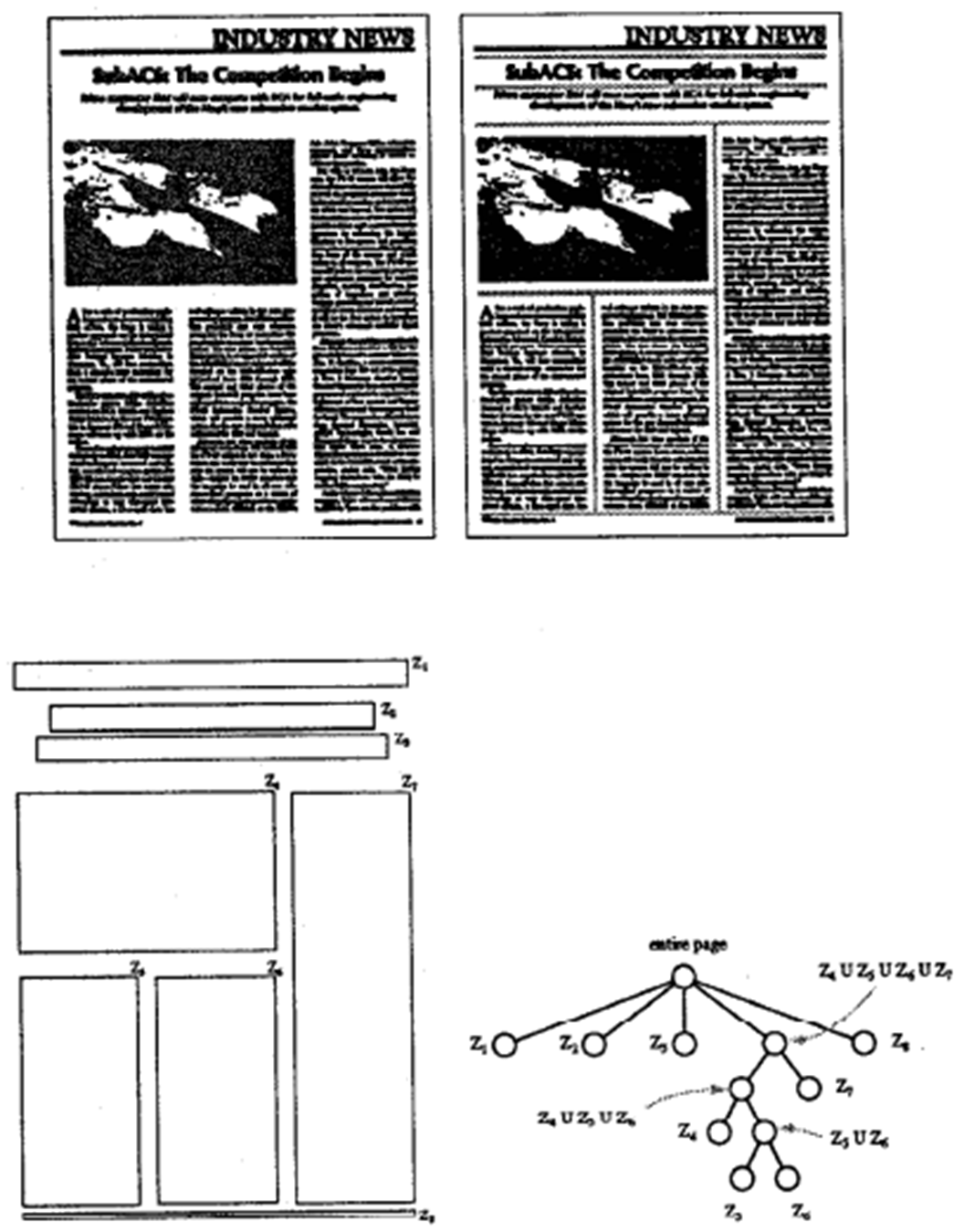
Авторы первоначальной статьи, похоже, считают своей основной заслугой это древесное представление. Они же заметили, что даже для «манхеттенского» документа возможно, что этот алгоритм не достигнет цели: к примеру, если блоки расположены вот так
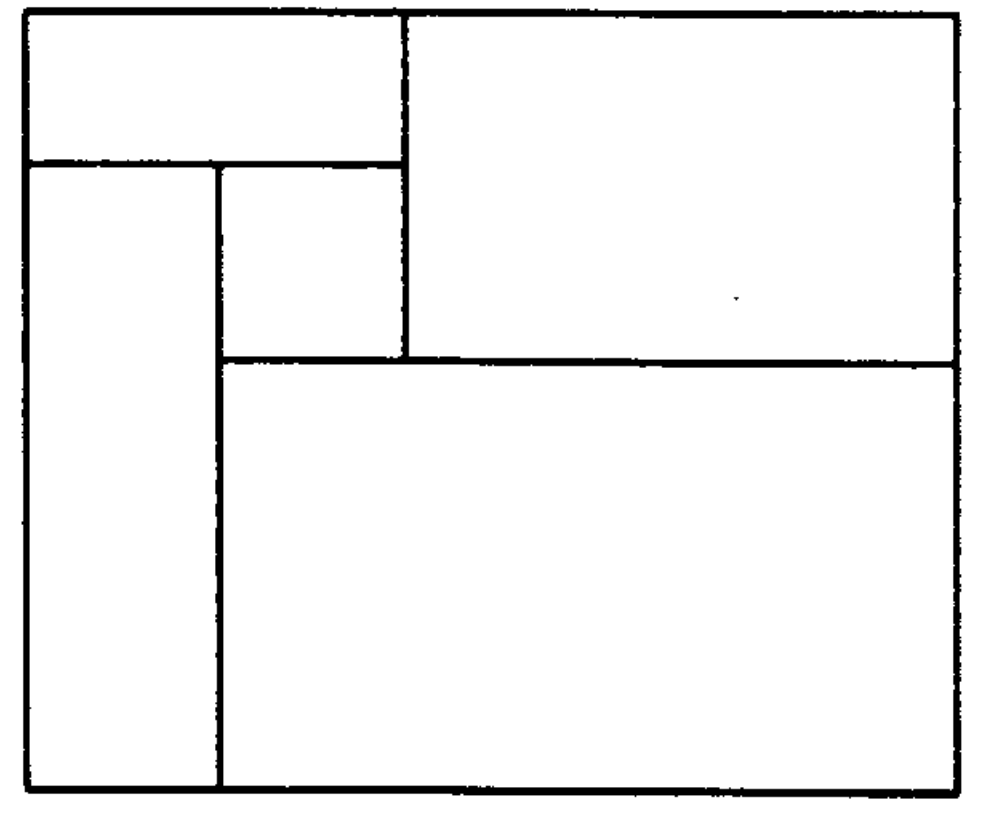
Прямо скажем, не самая распространённая конфигурация даже для газет, не говоря уж о журналах и офисных документах. Но встречается, в газетах уж точно.
Более серьёзной проблемой алгоритма видится всё же его подчинение порогам. Скажем на таком фрагменте будет сложно отделить заголовок от текста, не порвав при этом заголовок:
А здесь будет довольно трудно отделить картинку от текста, опираясь лишь на пороги по расстоянию:
Разумеется, актуальны ещё и общие для всех представленных в этом посте алгоритмов проблемы — как не оторвать нумерацию от нумерованного списка и как избавиться от ограничений, которые я указал в начале (что есть только текст и высококонтрастные картинки).
Сегментация с помощью максимальных белых прямоугольников
Теперь расскажем про идею сегментировать страницу с помощью максимальных белых прямоугольников. Что такое «максимальный белый прямоугольник»? Белый — это значит, что в нём нет чёрных точек (понятно, что изображение надо предварительно избавить от мелкого мусора). Максимальный — означает, что его нельзя увеличить ни влево, ни вправо, ни вверх, ни вниз так, чтобы он остался белым. Далее вместо чёрных точек мы будем рассматривать связные области. Как и в рекурсивных сечениях, мы можем их как-то сгруппирровать, но снова не будем на этом останавливаться. Понятно, что практически для каждой отсканированной страницы таких белых прямоугольников — десятки тысяч. Но для целей сегментации могут потребоваться только самые большие. Алгоритм их поиска предложен в статье Thomas M. Breuel. Two Geometric Algorithms for Layout Analysis
Вернёмся к задаче поиска максимальных белых прямоугольников. Можно ввести понятие «качество» для прямоугольника.
Назовём функцию качества Q( r ) для прямоугольника r монотонной, если при r1 ⊆ r2 выполняется Q(r1) <= Q(r2) — то есть если один прямоугольник лежит внутри другого, то качество внутреннего не может быть больше качества внешнего. Монотонных качеств придумать можно массу. Площадь годится. Периметр годится. Квадрат высоты плюс квадрат ширины годится. В общем, на что фантазии хватит.
Если качество монотонно, то применим следующий алгоритм, поиска максимальных белых прямоугольников, в порядке уменьшения качества.
- Заводим очередь с приоритетами для прямоугольников. Приоритет равен качеству.
- Кладём в очередь прямоугольник всей страницы. Он точно первый.
Далее в цикле:
- Достаём из очереди прямоугольник. Если он пуст, то это ещё один найденный максимальный белый прямоугольник.
- Если нет, из связных областей в исследуемом прямоугольнике выбираем одну «опорную» область (аналогично медиане в QSort). Здесь лучше не полагаться на случай, а сознательно выбрать что-то поцентральнее.
- Заметим, что максимальный белый прямоугольник может быть или целиком над этой областью, или целиком под ней, или справа от ней или слева (зелёные прямоугольники на рисунке ниже).
- Добавляем зелёные прямоугольники в очередь.
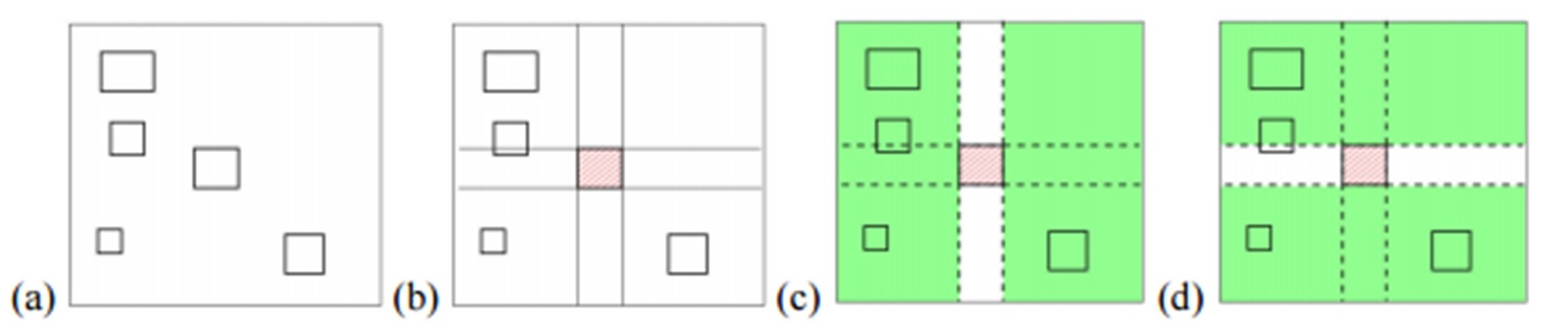
Условием выхода из цикла может быть или достаточное количество найденных прямоугольников, или качество текущего прямоугольника, взятого из очереди… На что фантазии хватит.
Хорошо, нашли мы максимальные белые прямоугольники. Посмотрим, что с ними дальше можно делать.
В той же статье Thomas M. Breuel не очень заморачивается на эту тему и пишет, что весь анализ делается в четыре шага:
- Найти все высокие максимальные белые прямоугольники и оценить их как кандидаты в межколоночные разделители
- В соответствии с найденной колоночной структурой найти строки
- Глядя на найденные строки, найти параграфы, структуру заголовков, колонтитулы
- Восстановить порядок чтения, используя и геометрическую и лингвистическую информацию
Далее в работе упомянуты некоторые разумные соображения о том, как именно надо классифицировать белые прямоугольники. Допускаю, что недостатков у функции оценки не так много — здесь мы скорее упрёмся в ограничения метода, чем в неправильность оценки.
Несколько иной подход описывает Henry Baird в своей работе Background structure in document images. В данной работе описан весьма интересный алгоритм, но реализация некоторых функций оставляет ощущение, что они специально “тонко настроены” на конкретной экспериментальной базе. Итак, предлагается поместить все найденные максимальные белые прямоугольники в приоритетную очередь. Конкретную функцию приоритета я приводить не буду, можете посмотреть в работе. Интуитивно понятно, что чем больше площадь прямоугольника и чем выше прямоугольник, тем приоритет должен быть больше.
Далее мы из этой очереди вынимаем прямоугольники, чтобы поместить некоторые из них в специальный список L. К каждому вынутому прямоугольнику применяем trimming rule: если этот прямоугольник пересёкся с какими-то элементами списка L, то вычитаем из него уже обработанные и то, что осталось, кладём обратно в очередь. В противном случае добавляем его в список L. Условие выхода из цикла какое-то слишком хитрое (я бы просто указал порог приоритета, но у авторов сложнее).
Вырезаем из страницы все прямоугольники списка L. Оставшиеся связные области на изображении объявляем готовыми текстовыми или картиночными блоками.
В качестве небольшого резюме по максимальным белым прямоугольникам можно сказать, что максимальный белый прямоугольник — очень важное понятие, крайне полезное для решение задачи сегментации страницы. По данным эксперимента из SKB, оба приведённых здесь алгоритма работают лучше и рекурсивных сечений, и Smearing’а. Другое дело, что в приведённых алгоритмах “замят” вопрос даже с картинками, не говоря уж о более сложных понятиях
Non-manhattan layout
Мы разобрали несколько алгоритмов для «манхеттенских» документов. Но что делать, если нам попался документ вот такого вида:
Ну, конкретно с этим ответ довольно простой — никакой это не документ, а просто обои у меня в туалете, так что что именно сделает с этой картинкой программа для обработки документов — не так уж и важно.
Если говорить всерьёз, то «неманхеттенский» layout — не такая уж большая экзотика, может встречаться и в газетах, и в журналах, а порой даже и в книгах. Вот типичный газетный пример:
Ниже мы разберём два алгоритма, которые справляются и с «неманхеттенскими» документами.
Docstrum
Слово Docstrum образовано по Кэрролловской продуктивной модели portmanteau word — склейкой слов Document и Spectrum (обожаю эту модель, кстати) и обозначает алгоритм сегментации «неманхеттенских» документов. Описал его O’Gorman в своей статье The document spectrum for page layout analysis в 1993 году. Сам метод придуман для страниц, которые лежали на сканере не идеально ровно, а под небольшим углом. Опишем, как этот алгоритм работает.
Для начала мы подготовим страницу, убрав мелкий мусор и большие явно нетекстовые объекты (ну или притворимся, что картинок на страницах не бывает — первый раз что ли?). Считаем, что всё, что осталось на странице — это буковки. Кластеризуем эти буковки по размеру (автор предложил ровно два кластера, но те, кто этот метод использовал, пробовали и три, и четыре, и ещё больше). Посмотрим расстояния от каждой буквы до k (обычно берут k равным 4 или 5) ближайших соседей из того же кластера. Запишем расстояния в гистограмму. Посмотрим на первые три пика гистограммы. Утверждается, что самый маленький пик — расстояние между буквами в слове, второй — межстрочное расстояние, третий — пробел. Если воспользоваться этим предположением, то можно исправить перекос, кстати.
Для сегментации страницы делаем транзитивное замыкание по близким компонентам — объединяем слова внутри строк и близкие строки друг с другом, получаем готовые блоки.
Помимо того, что данный метод позиционируется как работающий с «неманхеттенскими» документами, в нём явным образом используется важная идея. Я имею в виду свойство, что пороговые значения расстояний, от которых зависит наше решение (поместить два слова в один блок или нет), выбираются в зависимости от высоты слов. Это означает, что данный метод имеет хоть какие-то шансы регулярным образом справляться с неоднократно упоминаемой исследователями проблемой “over-segmenting of large fonts”.
С другой стороны, и здесь авторы ловко замяли вопрос, а что делать с картинками и более сложными объектами. Да и другие недостатки идеи опираться только на пороги по расстоянию мы уже обсудили выше.
Диаграмма Вороного
Диаграмма Вороного — интересный объект, который строится по произвольному набору точек плоскости (в нашем случае — по центрам букв). Точки, по которым строится диаграмма Вороного, здесь будем называть опорными точками. Она представляет собой разбиение плоскости на области; каждая область соответствует одной опорной точке и является множеством точек плоскости, для которых данная опорная точка ближе, чем любая другая опорная точка. Подробнее про диаграмму Вороного и её связь с другим любопытным объектом — триангуляцией Делоне, проще всего почитать по ссылкам в Википедию.
О том, как их можно построить, стоит читать в уже много раз цитируемой на Хабре прекрасной книжке А.В. Скворцова «Триангуляция Делоне и её применение». Я же расскажу о статье 1998 года K. Kise, A. Sato, and M. Iwata. Segmentation of page images using the area voronoi diagram. То есть о том, как диаграмму Вороного применили к решению задачи сегментации. Кстати, на сегодня этот способ считается “научным стандартом”, пока наука не предложила алгоритма, который был бы признанно лучше, чем данный. Да и в SKB авторы пишут, что диаграмма Вороного заметно опережает по качеству и белые прямоугольники, и Docstrum, и рекурсивные сечения.
Итак, привычным жестом мы очищаем картинку от мусора (всё, в последний раз за этот пост притворимся, что это и правда так легко сделать), центры оставшихся связных областей объявляем опорными точками и строим по ним диаграмму Вороного. Потом пометим, какие из ячеек диаграммы следует объединить. Объединяем ячейки в двух случаях:
- Или расстояние d между опорными точками (центрами связных компонент) меньше порога T1. Порог T1 подбирается таким образом, чтобы это правило занималось объединением соседних букв в словах
- Или для d выполнено следующее соотношение: d/T2+ar/Ta<1 где ar — это отношение площади большей связной области к площади меньшей (т.е. ar >= 1), а T2 и Ta — это ещё два порога. Смысл этого условия состоит в том, что стоит объединить два слова в строке, но если эти два слова имеют разную высоту, то объединять ячейки надо с большей осторожностью.
После того как нашли все ячейки, которые нужно объединить, объединяем их — и диаграмма Вороного превращается в готовую сегментацию.
В дальнейшем разные исследователи пытались улучшить работу диаграммы Вороного. Скажем, в статье 2009 года Voronoi++: A Dynamic Page Segmentation approach based on Voronoi and Docstrum features авторы M. Agrawal и D.Doermann рассказывают, как с помощью Docstrum и ещё другого странного колдунства половчее и поточнее подобрать порог T2. Про этот “улучшизм” я здесь не буду подробно писать, но само существование статей о развитии алгоритма сегментации, основанного на диаграмме Вороного, да ещё и написанных такими выдающимися учёными, как David Doermann намекает нам, куда ветер дует.
Недостатки диаграммы Вороного снова те же — ограничения зависят только от порогов, та же неясность с картинками. Несомненное достоинство данного метода состоит ещё и в том, что он содержит только три параметра, которые надо подобрать — и эти параметры указаны явным образом.
На этом я заканчиваю свой обзор научных достижений, связанных с сегментацией страницы. А наука, думаю, ещё своё слово скажет :)
Автор: ABBYY
