Введение
При решении задач моделирования движения объектов в трехмерном пространстве практически всегда требуется использование операций пространственных преобразований, связанных с умножением матриц преобразований и векторов. Для задачи N тел эта операция используется многократно для задания поворота и смещения тела относительно начала координат. Матрица пространственного преобразования имеет размерность 4х4, а размерность вектора, к которому применяется преобразование, соответственно 4x1. Рассмотрим оптимизацию выполнения такой операции с большим числом матриц и векторов под архитектуру Intel® Xeon Phi™.
В сопроцессоре Intel® Xeon Phi™ есть блок из 32 регистров длиной 512 бит (zmm00-zmm31). Соответственно, компилятор С++ от Интел [1] поддерживает набор векторных инструкций, работающих с этими регистрами, попадающий под спецификацию с кодовым названием KNC [2] (не путать с AVX-512). Этот набор инструкций ограничен, по сравнению с инструкциями AVX-512, но тем не менее включает операции, необходимые для решения рассматриваемой задачи. Высокоуровневые обертки над машинными инструкциями, поддерживаемые компилятором, называются функциями-интринсиками и описаны в качественной документации от Интел (Intel® Intrinsic Guide) [3]. Векторные регистры позволяют при правильной упаковке данных выполнять некоторую операцию сразу над набором данных (SIMD — single instruction multiple data). Далее будем использовать названия для регистровых переменных в коде, соответствующие именам регистров (zmm00-zmm31) и предполагать, что они отображаются на те же самые регистры при компиляции.
В пространственных преобразованиях распространены две операции: умножение матрицы на матрицу преобразования и умножение матрицы на вектор. Операцию умножения матриц преобразования в большинстве случаев можно свести к последовательности оптимизированных операций умножения матрицы на вектора-столбцы другой матрицы, поэтому операция умножения на вектор является наиболее интересной, и умножение матриц отдельно рассматривать не будем. Чтобы понять, как работает векторизация, рассмотрим простейший пример умножения матрицы 4x4 на вектор 4x1.
В этом случае происходит следующее:

где для наглядности пустым кружком показано поэлементное умножение векторов.
Если поместить в регистры столбцы матрицы и размножить по регистрам элементы вектора, операцию можно описать с помощью функций-интринсиков для умножения и FMA (fused multiply-add – смешанного умножения со сложением). То есть для получения в векторном регистре zmm00 вектора-результата надо загрузить столбцы матрицы в регистры zmm00-zmm03, элементы вектора размножить в регистры zmm04-zmm07, так, чтобы в каждом лежал многократно один элемент вектора, а затем выполнить 3 операции:
zmm00=_mm512_mul_ps(zmm00, zmm04);
zmm00=_mm512_fmadd_ps(zmm01, zmm05, zmm00);
zmm00=_mm512_fmadd_ps(zmm02, zmm06, zmm00);
zmm00=_mm512_fmadd_ps(zmm03, zmm07, zmm00);Чтобы расположить столбцы матриц в регистрах можно использовать транспонирование, если матрица хранится по строкам, но это трудоемкая операция, поэтому лучше всего хранить матрицы по столбцам. И комбинировать преобразования так, чтобы получались матрицы по столбцам.
В данном примере с вещественными 32-битными числами (суффикс ps) регистры используются только на четверть, так как в 512-битный регистр помещается 16 элементов, а в нашем случае только 4, то есть имеет место проигрыш в 4 раза. Если использовать двойную точность (эквивалентный код с суффиксом pd), то регистры будут заполнены наполовину. Даже такие варианты частичного заполнения регистров могут дать ускорение если использовать по 4 элемента из векторного регистра с результатом для сохранения, так как выполняются сразу 4 операции, вместо одной.
Особенности загрузки и выгрузки данных
Для повышения эффективности загрузки данных из памяти в регистры и выгрузки из регистров в память выделенная в программе память должна быть выровнена по границе в 64 байта. В этом случае можно использовать операции _mm512_load и _mm512_store с соответствующими суффиксами для типов данных.
Для динамического выделения выровненной памяти в компиляторе реализованы специальная функция _mm_malloc, которая используется в связке с _mm_free. От обычной функции malloc отличие в том, что добавлен второй аргумент – кратность границы выравнивания памяти, для 512-битных регистров должен возвращаться указатель на память с адресом, кратным 64 байтам. Для типа Type синтаксис выделения выровненной памяти следующий:
Type* pointer = (Type*)_mm_malloc(sizeof(Type)*N, 64);Для статических массивов данных также предусмотрены директивы выравнивания памяти, например, для определения выровненного массива в компиляторе Интел предусмотрен следующий синтаксис:
__declspec(align(64)) Type mem[N];Можно также использовать поддерживаемый *nix – вариант:
Type mem[N] __attribute__((aligned(64)));В случае невозможности выровнять память необходимо использовать интринсики для работы с невыровненной памятью _mm512_loadu и _mm512_storeu. По непонятным причинам в компиляторе не реализованы функции загрузки в регистры из невыровненной памяти и выгрузки из регистров в невыровненную память для KNC, для AVX-512 такие функции есть.
Для KNC эти функции можно реализовать самостоятельно на основе интринсиков для частичной загрузки до границы выравнивания:
inline __m512d _mm512_loadu_pd(const double* a)
{
__m512d reg = _mm512_setzero_pd();
reg =_mm512_loadunpacklo_pd(reg, a);
reg =_mm512_loadunpackhi_pd(reg, a+8);
return reg;
}Аналогично выглядит функция выгрузки:
inline void _mm512_storeu_pd(double* a, __m512d reg)
{
reg =_mm512_packstorelo_pd(a, reg);
reg =_mm512_packstorehi_pd(a+8,reg);
return reg;
}Правильное использование выровненной памяти может приводить к ускорению до 3 раз, поэтому далее будем рассматривать только работу с выровненной памятью.
Оптимизация со специальным хранением матриц в памяти
В наиболее общем случае для чисел одинарной точности можно заметить, что матрицы загружаются полностью в один регистр. Если элементы матриц хранить последовательно, то при загрузке получаем регистр с 16 элементами одной матрицы. Это хорошо для операций векторного умножения, но плохо для сложения, потому что складывать элементы необходимо внутри регистра. Операции сложения элементов внутри регистра связаны с медленными инструкциями перемешивания, сдвига и перестановки элементов, или редукции, так как операций горизонтального сложения в наборе инструкций KNC нет. Если написать сложный алгоритм, который делает это на интринсиках, получается более медленный код, чем сгенерированный компиляторным оптимизатором.
Для минимизации числа инструкций нам необходимо, чтобы вычисления делались следующим образом:

Чтобы посчитать сразу 4 вектора результата, имеет смысл расположить данные в памяти так, чтобы строки матрицы лежали поочередно, и за один набор инструкций выполнялось умножение сразу 4 матриц на 4 вектора. Для этого необходимо записывать новые элементы матриц в следующем порядке:

Отсюда видно, что необходимо хранить сначала первые столбцы, потом вторые, потом третьи и в конце четвертые сразу для 4 матриц. За одну операцию загрузки в регистр будут помещаться 16 элементов:

По аналогии вектора тоже следует расположить по первым, вторым, третьим и четвертым элементам сразу 4 векторов. Но, как правило, это неудобно, так как вектора всегда используются как последовательности элементов для сложения, определения положения тел в пространстве, в то время как матрицы поворота обычно вычисляются из тригонометрических преобразований, а ориентация тела задается системой углов (например, углы Эйлера) или кватернионами. То есть в вычислительном коде вектора должны храниться последовательно для быстрого обращения к ним. Матрицы могут храниться произвольно, так как они вычисляются через параметры, описывающие ориентацию, а единственную необходимую операцию с ними мы как раз векторизуем специальным образом с учетом этого особого хранения.
Исходя из последовательного хранения векторов рассмотрим, как можно получить необходимые нам последовательности элементов. То есть, если мы имели в памяти вектор

то необходимо получить следующий набор регистров

Используя инструкцию размножения элементов, мы можем загрузить в 4 регистра элементы a1, b1, c1, d1:
zmm08 = _mm512_extload_ps(vec + 0,
_MM_UPCONV_PS_NONE, _MM_BROADCAST_1X16, _MM_HINT_NONE);
zmm09 = _mm512_extload_ps(vec + 4,
_MM_UPCONV_PS_NONE, _MM_BROADCAST_1X16, _MM_HINT_NONE);
zmm10 = _mm512_extload_ps(vec + 8,
_MM_UPCONV_PS_NONE, _MM_BROADCAST_1X16, _MM_HINT_NONE);
zmm11 = _mm512_extload_ps(vec + 12,
_MM_UPCONV_PS_NONE, _MM_BROADCAST_1X16, _MM_HINT_NONE);После этого есть возможность смешать их необходимым нам образом с помощью битовых масок:
zmm06 = _mm512_mask_blend_ps(mask32_0, zmm08, zmm09);
zmm07 = _mm512_mask_blend_ps(mask32_1, zmm10, zmm11);
zmm04 = _mm512_mask_blend_ps(mask32_2, zmm06, zmm07);Для наглядности на рисунке показано, как работают загрузка и перемешивание элементов в регистрах.
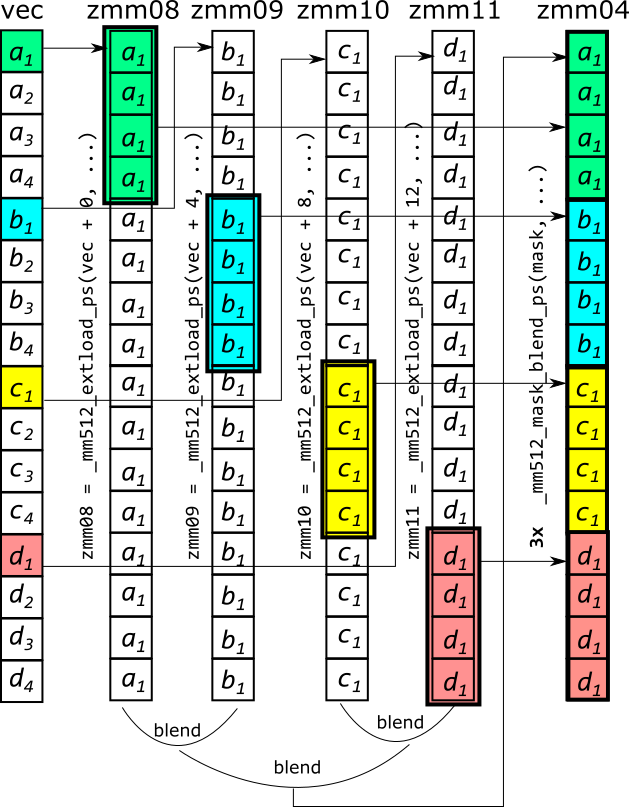
Смешивать можно только 2 регистра, поэтому операция повторяется 3 раза с разным значением маски. После этого имеем необходимое нам содержимое в регистре zmm04. Аналогичные операции загрузки-перемешивания позволяют получить необходимые элементы векторов в регистрах zmm05-zmm07, после чего можно выполнять операции умножения и сложения для получения результата. Такой способ можно применить на процессорах с поддержкой инструкций AVX-512 и KNC.
Можно заметить, что элементы векторов необходимо частично дублировать четверками в соответствующих четвертях регистрах. Для этого в наборе инструкций KNC для Intel® Xeon Phi™ есть специальная операция swizzle, позволяющая переставлять и размножать элементы в четвертях регистров. В случае загрузки 4 векторов с последовательным следованием элементов следующий код преобразует его в необходимые множители:
zmm04 = _mm512_swizzle_ps(zmm08, _MM_SWIZ_REG_AAAA);
zmm05 = _mm512_swizzle_ps(zmm08, _MM_SWIZ_REG_BBBB);
zmm06 = _mm512_swizzle_ps(zmm08, _MM_SWIZ_REG_CCCC);
zmm07 = _mm512_swizzle_ps(zmm08, _MM_SWIZ_REG_DDDD);Как работает swizzle, показано на рисунке.

Если мы имели в регистре zmm08 вектор последовательных элементов vec, то в результате работы этих инструкций, сформируются необходимые нам zmm04-zmm07. Последний вариант содержит существенно меньше инструкций, но не применим для набора инструкций AVX-512, поэтому следует выбирать максимально подходящие инструкции для конкретной архитектуры и использовать их.
Для демонстрации преимущества по времени выполнения, полученного в результате оптимизации кода, было проведено тестирование умножений большого числа матриц преобразования на векторы, заполненные случайными числами. Для сравнения использовался тест умножения 300000 матриц преобразования на сопроцессоре Intel® Xeon Phi™ 5120D.
Сравнение результатов оптимизации проводилось после предварительного прогревочного запуска этого же кода. После прогрева выбиралось среднее время из 10 последующих запусков. Чтобы избежать оптимизации неиспользуемого кода, также была создана искусственная зависимость по данным (результаты операции записывались в вектор-множитель для следующей операции). Результаты для 32 и 64-битных вещественных чисел показаны в таблице 1, где в столбце авто находится результат для автовекторизации.
Таблица 1 – Замеры времени и ускорение оптимизированного кода
| тип | время, с авто | время, с blend | время, с swizzle | ускорение blend | ускорение swizzle |
|---|---|---|---|---|---|
| 32 | 1.15 | 0.34 | 0.2 | 3.38 | 5.75 |
| 64 | 1.41 | 0.55 | 0.45 | 2.56 | 3.13 |
Оптимизация с обыкновенным хранением матриц
В некоторых случаях матрицы переупорядочить нельзя, поэтому необходимо делать их загрузку особым образом. Рассмотрим алгоритм преобразования матриц для двойной точности (для одинарной все аналогично, но очень громоздко). В случае двойной точности нам необходимо в каждый умножаемый регистр с элементами матриц поместить 2 набора по 4 элемента. В наборе инструкций KNC есть операция склеивания со сдвигом вправо, которая совмещает 2 регистра в последовательность из 1024 бит, после чего смещает его на заданное число элементов вправо и записывает в результирующий регистр младшие 512 бит. Операция представлена только для целочисленного типа данных, хотя в инструкциях AVX-512 она присутствует и для вещественных, но из-за одинакового битового представления нам тип данных не важен. Нужно иметь ввиду только то, что число сдвигаемых элементов должно быть в 2 раза больше для чисел двойной точности. Путь имеется две матрицы, которые хранятся как последовательность столбцов:

Для начала загружаем матрицы, которые хранятся по столбцам последовательно:
__m512i izmm10 = _mm512_load_epi64(pmtx); //A2-A1
__m512i izmm11 = _mm512_load_epi64(pmtx+8); //A4-A3
__m512i izmm12 = _mm512_load_epi64(pmtx+16); //B2-B1
__m512i izmm13 = _mm512_load_epi64(pmtx+24); //B4-B3В результате операции в izmm10-izmm11 – первая матрица, в izmm12-izmm13 – вторая. Нам необходимо поместить первые строки обеих матриц в регистр zmm00, вторые – в zmm01, третьи – в zmm02, четвертые – в zmm03. Для этого используем склеивание со сдвигом на 256 бит (8 целых чисел или 4 вещественных числа двойной точности):
izmm14 = _mm512_alignr_epi32(izmm10, izmm12, 8); //A1-B2
zmm00 = (__m512d)_mm512_alignr_epi32(izmm12, izmm14, 8); //B1-A1
zmm01 = (__m512d)_mm512_alignr_epi32(izmm14, izmm10, 8); //B2-A2
izmm14 = _mm512_alignr_epi32(izmm11, izmm13, 8); //A3-B4
zmm02 = (__m512d)_mm512_alignr_epi32(izmm13, izmm14, 8); //B3-A3
zmm03 = (__m512d)_mm512_alignr_epi32(izmm14, izmm11, 8); //B4-A4На рисунке показано, как это работает.
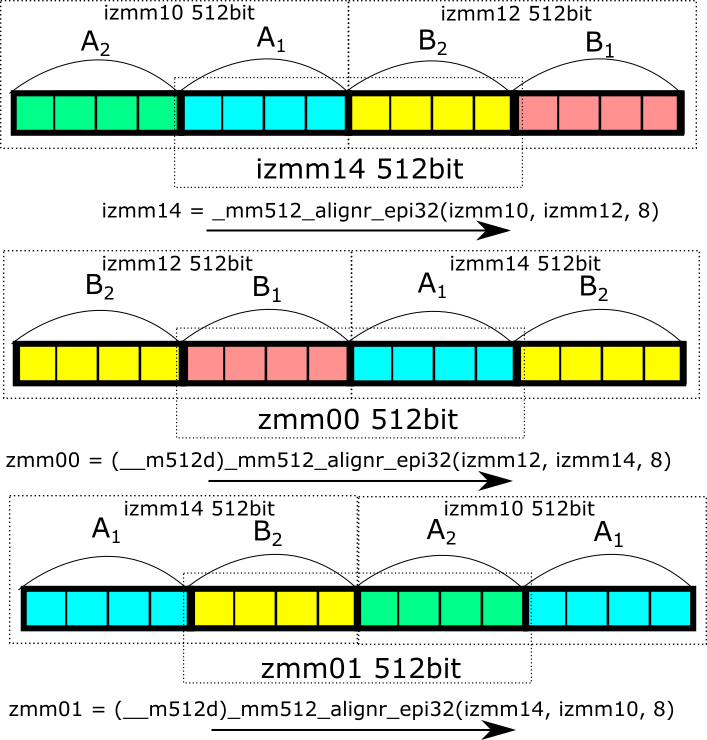
В результате операции в регистрах zmm00-zmm03 получаем требуемую последовательность столбцов матриц. После этого использование swizzle для загрузки векторов в регистры zmm04-zmm07 и последующее применение FMA-инструкций, как это делалось раньше, позволяет получить результат для двух операций умножения матриц преобразований на два вектора в регистре zmm00.
zmm04 = _mm512_swizzle_pd(zmm08, _MM_SWIZ_REG_AAAA);
zmm05 = _mm512_swizzle_pd(zmm08, _MM_SWIZ_REG_BBBB);
zmm06 = _mm512_swizzle_pd(zmm08, _MM_SWIZ_REG_CCCC);
zmm07 = _mm512_swizzle_pd(zmm08, _MM_SWIZ_REG_DDDD);
zmm00=_mm512_mul_pd(zmm00, zmm04);
zmm00=_mm512_fmadd_pd(zmm01, zmm05, zmm00);
zmm00=_mm512_fmadd_pd(zmm02, zmm06, zmm00);
zmm00=_mm512_fmadd_pd(zmm03, zmm07, zmm00);Аналогично можно реализовать код для четырех операций умножения матриц на четыре вектора с 32-битными вещественными числами. Если сравнить замеры времени, можно оценить потери, связанные с предварительным преобразованием матриц (таблица 2), тем не менее даже этот код дает ускорение более чем в 2 раза, по сравнению с кодом, сгенерированным компилятором.
Таблица 2 – Замеры времени и ускорение с разным хранением матриц
| хранение матриц | время, с авто | время, с swizzle |
ускорение swizzle |
|---|---|---|---|
| черезстрочное | 1.41 | 0.45 | 3.13 |
| обыкновенное | 1.25 | 0.56 | 2.23 |
Заключение
Оптимизация кода для пространственных преобразований с матрично-векторным умножением для сопроцессора Intel® Xeon Phi™ позволяет получить более быстрый код, по сравнению с компиляторной оптимизацией, если грамотно использовать доступный набор векторных инструкций и организовать эффективное хранение данных в памяти.
Ссылки
[1]. Intel® C++ Compiler 16.0 User and Reference Guide//
https://software.intel.com/en-us/intel-cplusplus-compiler-16.0-user-and-reference-guide
[2]. Intel® Xeon Phi™ Coprocessor Instruction Set Architecture Reference//
https://software.intel.com/sites/default/files/forum/278102/327364001en.pdf
[3]. Intel® Intrinsic Guide//
https://software.intel.com/sites/landingpage/IntrinsicsGuide/
Автор: Intel