На Хабре уже писали о простом алгоритме создания стереограмм. Стереограмма в нём генерируется на основе карты высот и изображения с повторяющимся рисунком. В данной статье я хочу описать другой подход к созданию стереограмм – на основе трехмерной модели. Основные отличия описанного здесь алгоритма от алгоритма, указанного выше:
- вместо карты высот (которая по сути представляет из себя карту смещений пикселей по горизонтали) объекты задаются непосредственно в трехмерных координатах;
- нет ограничений на количество объектов и их расположение (за исключением того, что все они должны находиться в поле зрения и на некотором расстоянии от плоскости стереограммы – для того, чтобы их можно было увидеть), тогда как при использовании карты высот мы имеем дело только с одним слоем;
- созданная стереограмма обладает перспективой (чем дальше от наблюдателя находится объект, тем меньшим он выглядит);
- вид объекта зависит от ракурса, с которого он виден (как и для реальных объектов).
Терминология
Стереограммой называется изображение или пара изображений, при просмотре которых создается стереоэффект (у наблюдателя появляется ощущение глубины изображения). К стереограммам относятся, например, анаглифные изображения и автостереограммы. Автостереограмма – это стереограмма, состоящая из одного изображения и не требующая никаких дополнительных приспособлений для просмотра (вроде анаглифных очков или стереоскопа). В этой статье мы рассматриваем именно автостереограммы.
Суть алгоритма
Задача состоит в создании такого изображения на плоскости, чтобы при взгляде на него оба глаза видели такую же картинку, какую бы они видели, если бы вместо этого изображения они наблюдали реальный трехмерный объект (рис. 1).
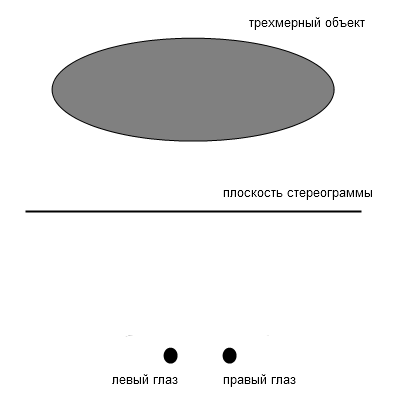
Рис. 1.
Если считать, что у наблюдателя только один глаз (глаз будем считать точкой), то задача сводится к центральной проекции трехмерного объекта на плоскость (центральную проекцию точки объекта можно получить, соединив прямой точку объекта с точкой глаза – точка пересечения полученной прямой с плоскостью и будет центральной проекцией; точка глаза называется центром проекции). Но у нашего наблюдателя два глаза, потому обе проекции объекта нужно будет сопоставить между собой.
Рассмотрим точку T1 трехмерного объекта (рис. 2). Эта точка находится на видимой части объекта. Проекцией этой точки на плоскость для левого глаза будет P1, для правого – P2. Поскольку для левого глаза видимое положение точки T1 совпадает на плоскости с видимым положением точки P1, а для правого глаза – с положением точки P2, то точки P1 и P2 должны иметь одинаковый цвет, совпадающий с цветом точки объекта T1, чтобы зрительная система корректно сопоставила изображения с правого и левого глаз. Далее, найдем на объекте ближайшую для левого глаза точку, чтобы её проекция на левый глаз совпадала с точкой P2. Это будет точка T2. Точка P3 является проекцией T2 на правый глаз, и должна быть окрашена в тот же цвет, что и P1 и P2.
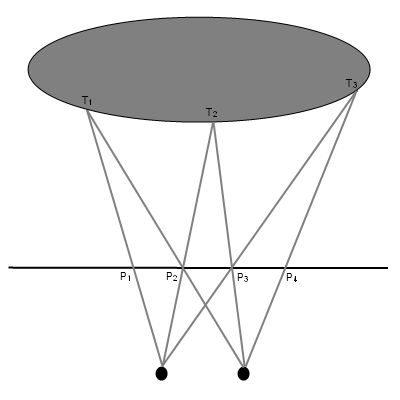
Рис. 2.
Процесс получения последовательности точек P1, P2, P3 … повторяется до тех пор, пока не будет выполнено одно из условий:
- проекция для правого глаза очередной точки объекта на плоскость лежит за пределами создаваемого изображения (если мы не собираемся создавать стереограмму бесконечного размера);
- очередная точка объекта Tk не является видимой для правого глаза, т.е. существуют точка, находящаяся ближе к глазу, и проекции точек для правого глаза совпадают;
- для очередной точки проекции на правый глаз Pj не существует точки на объекте, проекция которой на левый глаз совпадала бы с Pj (обычно такая ситуация невозможна – позади объектов создается плоскость или другая фигура, выступающая в качестве фона и занимающая все поле зрения).
Собственно, алгоритм заключается в разбиении стереограммы на такие группы точек и выбора для каждой группы некоторого цвета (т.к. все точки группы должны иметь одинаковый цвет, назовем такие группы одноцветными).
Мы считаем, что глаза расположены на одной высоте и находятся на одинаковом расстоянии от плоскости стереограммы. Как следствие, пучки лучей, выпущенные из обоих глаз и проходящие через горизонтальную прямую на плоскости проекции, будут лежать в одной плоскости. Пучки лучей, проходящие через разные горизонтальные прямые, будут находиться в разных плоскостях, пересекающихся в прямой, соединяющей глаза. Таким образом, все точки P1 … PN одной одноцветной группы будут расположены на одной горизонтальной прямой.
Мы рассмотрели объект, находящийся за плоскостью стереограммы. Для объектов, находящихся перед плоскостью, способ построения изображения аналогичен. Отличие только в том, что если для объекта, лежащего за плоскостью, очередная точка проекции Pj+1 лежит правее чем Pj, то для объекта, лежащего перед плоскостью, точка Pj+1, наоборот, будет лежать левее точки Pj. Можно построить стереограмму, содержащую объекты, лежащие с обеих сторон от плоскости стереограммы, но важно учитывать некоторые ньюансы. Каждая следующая точка некоторой последовательности P1 … PN в такой стереограмме может быть как правее, так и левее предыдущей. Следовательно, возможно образование циклов. Другим следствием является то, что одна одноцветная группа может содержать довольно большое количество точек, что может испортить внешний вид стереограммы и усложнить её просмотр. И вообще, одновременное наблюдение объектов, находящихся по обе стороны плоскости стереограммы, невозможно: при фокусировке зрения за плоскостью, объекты, находящиеся перед плоскостью, будут видны также за плоскостью, но с инвертированной глубиной. При фокусировке перед плоскостью будет возникать аналогичная проблема.
Детали реализации
Наша стереограмма представляет из себя прямоугольник на плоскости в трехмерном пространстве, разбитый на сетку прямоугольных пикселей. Для удобства продолжим сетку пикселей во все стороны, заполнив ею всю плоскость стереограммы. Немного упростим задачу – будем рассматривать только те точки пространства, которые находятся перед глазами (для которых луч, проведенный из глаза, пересекает плоскость стереограммы). Центральная проекция произвольной точки на плоскость стереограммы будет попадать в один из пикселей. А раз у нас два глаза, то каждой точке пространства соответствует два пикселя, содержащие проекции точки на левый и правый глаза. Множество точек, которым соответствует заданная пара пикселей, назовем кластером (по сути, такой кластер – это пересечение двух телесных углов, выходящих из глаз и стянутых соответствующими пикселями). Угловые размеры кластера равны угловым размерам пикселя, через который виден кластер (см. рис. 3).
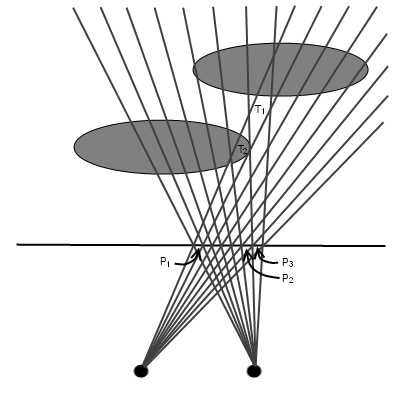
Рис. 3. T1 и T2 – кластеры, P1, P2, и P3 – пиксели.
Алгоритм заключается в следующем: для каждого пикселя находится ближайшая (относительно глаза) точка среди точек объекта, проекция которых попадает в данный пиксель (иными словами, берется видимая через данный пиксель точка). Это делается либо путем пересения лучей, выходящих из глаза и проходящих через каждый пиксель, с фигурой (подходит для простых фигур вроде многоугольника или сферы), либо путем вычисления значения некоторой функции поверхности в точках координатной сетки. Подробности можно увидеть, изучив исходники алгоритма (ссылку см. в конце статьи). Данная процедура последовательно выполняется для каждого глаза. Причем, расстояние до ближайшей найденной точки хранится не в виде длины отрезка или координаты Z, а в виде координаты кластера. А поскольку кластер задается координатами двух пикселей, то для данного пикселя достаточно хранить координаты пикселя, являющегося проекцией кластера на другой глаз (причем для сравнения расстояний от глаза до кластера достаточно сравнивать координаты другого пикселя). Таким образом, для каждого пикселя мы храним только координаты двух других пикселей, соответствующие двум кластерам.
Поясним сказанное на примере из рис. 3. Рассмотрим кластеры T1 и T2, имеющие общую проекцию P1 для левого глаза. Их проекции для правого глаза – соответственно P3 и P2. Но P2 находится левее, чем P3. Следовательно, кластер T2 ближе к левому глазу, чем T1.
Использование кластеров удобно еще и тем, что позволяет легко получить одноцветные группы точек. Для пояснения снова обратимся к рис. 3. Для P1 координата ближайшего кластера для левого глаза задается в виде пары (P1, P2). Для P2 координата ближайшего кластера для правого глаза – тоже (P1, P2). Это значит, что глаза через пиксели P1 и P2 видят общий кластер, а следовательно, пиксели P1 и P2 относятся к одной одноцветной группе. Для P3 координата ближайшего кластера для правого глаза – (P1, P3), что не совпадает с координатой ближайшего кластера для левого глаза для P1. Т.е. кластер (P1, P3) заслонен от левого глаза более близким кластером, а пиксели P1 и P3 относятся к разным одноцветным группам (пиксель P3 является крайним в своей группе). Одному пикселю соответствует не более одного кластера для каждого глаза, а одному кластеру – не более одного пикселя для каждого глаза, что делает алгоритм разбиения на одноцветные группы достаточно простым.
Осталось выбрать цвета для одноцветных групп. Их можно выбрать либо случайным образом, либо на основе фонового изображения (причем фоновое изображение не обязано иметь повторяющиеся части). В описываемом алгоритме реализованы оба варианта (см. исходники).
Теперь же посмотрим на результат работы алгоритма (рис. 4). В данной стереограмме изображено несколько сфер и плоскость, параллельная плоскости стереограммы, в качестве фона. Цвета пикселей генерируются случайным образом.

Рис.4. По клику — стереограмма в разрешении 1024x768.
Если присмотреться к сферам, то на них можно заметить ступеньки, словно сферы состоят из плоскостей, параллельных стереограмме. Расстояние между повторяющимися частями стереограммы задает глубину объектов (чем расстояние больше, тем более удаленным выглядит объект). Разница в расстоянии всего в один пиксель уже дает заметное отличие в глубине. Данную проблему можно решить, либо увеличив разрешающую способность устройства, либо модифицировав алгоритм. Мы пойдем по второму пути. Для этого уменьшим ширину наших виртуальных пикселей в несколько раз, увеличив во столько же раз их количество по горизонтали. Затем, при генерации изображения, будем объединять несколько субпикселей в один пиксель (беря в качестве цвета пикселя среднее арифметическое цветов субпикселей). На рис. 5 видно, что ступенек уже нет (здесь берется 3 субпикселя на пиксель, потому шаг повторяющихся частей изображения кратен 1/3 пикселя).

Рис. 5. По клику — стереограмма в разрешении 1024x768.
На рис. 6 приведен пример изображения-карты высот. А на рис. 7 показана стереограмма с объектом, созданным на основе данной карты высот. Карта высот рассматривается как набор точек в пространстве, координаты которых задаются на основе координат пикселей и их цветов. На основе точек создаются треугольники, соединяющие соседние точки (подробности см. в исходниках), благодаря чему объект выглядит сплошным, а не набором точек. Используя произвольный базис, можно искажать и вращать объект (координаты точки вычисляются как V1*x+V2*y+V3*z, где x и y – координаты пикселя на карте высот, z – его цвет, V1, V2, V3 – базис). В отличие от предудыщих стереограмм, здесь цвета берутся на основе заданного фонового изображения.

Рис. 6. По клику – изображение в исходном разрешении.

Рис. 7. По клику — стереограмма в разрешении 1024x768.
Ссылки
- en.wikipedia.org/wiki/Autostereogram – общая информация об автостереограммах;
- github.com/Domanser/AutoStereogramDemo – исходный код описанного алгоритма (C# 4.0), а также примеры создания стереограмм, приведенных в данной статье, и некоторых других.
Автор: Domanser





